DemonScript примеры: Лампочки и провода

Постановка задачи
Базовые отношения
Провод как палка
Целевые аксиомы

Тестируем простую модель
Вывод всех моделей
Добавляем вилку с розеткой

Постановка задачи

Пусть есть следующие множества объектов:

lamp (лампочка) - может либо гореть, если к ней подведено напряжение, либо не гореть;
wire (провод) - может проводить ток;
socket (розетка) - служит для подключения электрической вилки или провода;
fork (электрическая вилка) - может быть вставлена в розетку и подключена к проводу;
power (источник напряжения) - благодаря ему лампа может гореть.

Это перечень абстрактных классов, конкретные экземпляры которых будут участвовать в задаче. Наша цель состоит в построении аксиоматики этих сущностей, позволяющей понимать горит ли лампа при данном соединении объектов или нет. Для простоты, будем считать, что напряжение переменное, провод - это "пара проводов", рассматриваемых как целый объект. Поэтому, хотя на диаграммах соединения объектов будут линейными (рисунок слева), подразумевается параллельное соединение (справа):

Ниже приведены примеры в которых лампочки горят:

В этих же примерах лампочка гореть не будет:

При этом, во втором примере одна лампа горит, а вторая - нет. В третьем примере происходит короткое замыкание, при котором и лампа и источник портятся.

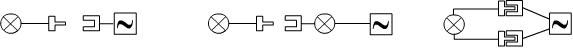
Базовые отношения

В DemonScript есть два базовых отношения: X.@isa.Y (X является подмножеством или элементом класса Y) и X.@attr.Y (X имеет атрибут Y). Их объявлять не нужно. Дополнительно, введём ещё два отношения: X.@ato.Y и X.@bind.Y. Первое отношение @ato (= attach to)означает, что два объекта непосредственно прикреплены друг к другу: провод прикручен к лампочке, вилка вставлена в розетку и т.д.. Второе отношение @bind означает, что два объекта связаны либо непосредственно (как @ato), либо через цепочку других объектов и соединений (лампа @bind к источнику power через провод wire).

Начнём с определения иерархии абстрактных классов, граф которых назовём Sen:

edges @ato, @bind                  // типы рёбер

var Sen = GRAPH("Sen")             // создаём конструктором пустой граф без узлов
GRAPH = Sen                        // делаем его текущим и добавляем узлы:
global Sen                         // эта переменная будет доступна в демонах

nodes $lamp, $wire, $socket, $fork, $power             
nodes $glow, $break

Кроме уже упомянутых сущностей, введены ещё две, которые будут использоваться как атрибуты объектов. Атрибут $glow означает, что лампа горит, а $break означает, что лампа или источник сломаны (перегорели).

Отношение @ato будем считать антирефлексивным (1). Это означает, что объект сам к себе привязать нельзя: !X.@ato.X (провод будет проанализирован отдельно). Это отношение также симметрично (2): если Y привязан к X, то и X привязан к Y (ньюансов нет). Наконец, если два объекта привязаны (@ato) друг к другу, то они одновременно соединены (@bind). Отношение @bind симметрично и ограниченно транзитивно:

var X,Y,Z
Mind.add(
  !X.@ato.X,                                      // (1)
   Y.@ato.X -> X.@ato.Y,                          // (2)
   X.@ato.Y -> X.@bind.Y,                         // (3)    
   
   Y.@bind.X  -> X.@bind.Y,                       // (4)
   X.@bind.Z  &  Z.@bind.Y & X!=Y -> X.@bind.Y)   // (5)

Заметим, что, в отличии от антирефлексивного @ato, отношение X.@bind.X может оказаться истинным, когда цепочка присоединённых к X объектов образует петлю. Ограниченная транзитивность отличается от просто транзитивности членом X!=Y. Если бы его не было, то при X==Y мы бы имели: X.@bind.Z & Z.@bind.X -> X.@bind.X или, в силу симметрии, X.@bind.Z -> X.@bind.X. Понятно, что тогда присоединение X с любым Z приводило бы к "самоприсоединению" X.

Добавим ещё одну аксиому, которая будет делать вывод, что объект, не присоединённый ни к какому другому объекту (т.е. об этом есть явная информация), не может быть ни с кем связан. Для этого определим демона изолированного объекта:

def isolated(X):
   return forall(Z, !X.@ato.Z)

Mind.add(
   isolated(X) -> !X.@bind.Y )                    // (6)

Напомним, что демоны в аксиоме только сообщают логическое значение, но ничего не меняют в графе отношений. В отличии от этого, ребро X.@bind.Y при логическом выводе может поменять своё значение, если посылка isolated(X) окажется истинной. В демоне isolated(X) вызывается функция forall, которая для всех узлов Z текущем графа проверяет выполнимость условия, стоящего во втором аргументе.

Задачу будем решать в несколько итераций. Сначала рассмотрим упрощённую модель, после чего она будет постепенно усложняться.

Провод как палка

В начале ограничимся тремя сущностями: lamp, power и wire. Проводу, как и остальным объектам, пока запретим присоединяться к самому себе (в петлю) и дважды присоединяться к лампочке или источнику. Впрочем, последнее и невозможно. Так как объекты не имеют частей (пока), если установлено отношение $wire.@ato.$lamp = True, "второй раз" (ещё одно соединение) установить нельзя. В этой упрощённой модели представляем себе провод как "несгибаемый стержень".

Будем считать, что к лампочке lamp можно присоединять только провода, и при этом не более двух (см. рисунки выше). К источнику можно присоединить любое число проводов. Провод может присоединяться к объектам любых классов, но не более чем два раза.

Опишем эти знания при помощи аксиом. Для этого определим сначала нескольких демонов:

def isa (X, Y) : return X.isa(Y)? True: False
def ato(X, Y)  : return X.@ato.Y == True | Y.@ato.X == True

Первый - возвращает True, если X является экземпляром класса Y. В этом демоне вызывается встроенная функция .isa поиска пути по графу, по рёбрам @isa от узла X к узлу Y. Эта функция может "путешествовать" по связанным графам, поэтому, если X - конкретный объект сознания $lamp1, а $lamp - абстрактный класс, определённый в графе Sen, то isa($lamp1, Sen=>$lamp) вернёт True, если $lamp1 объявлен как экземпляр класса лампочек. В общем случае функция X.isa(Y) может вернуть три значения:

True - если путь есть и все его рёбра истинные;
False - если в пути последнее ребро ложное;
Undef - пути нет, т.е. нет информации о принадлежности X к Y.

Определённый же выше демон будет бинарным (True, False), т.е. мы будем считать, что если прямо не указано, что X принадлежит Y, то он ему не принадлежит. Аналогично, бинарный демон ato, возвращает True если объекты присоединены и False - если нет или отстутствует информация.

Остальные демоны также бинарным функциями, сообщающими что к объекту X (который должен соответствовать имени демона можно присоединить объект Y:

def can_power_ato(X,Y) :
   return isa(Y, Sen=>$wire)

def can_wire_ato(X,Y) :
   return ato(X, Y) | X.count_in(@ato) < 2

def can_lamp_ato(X,Y) :
   return ( ato(X, Y) | X.count_in(@ato) < 2 ) & isa(Y, Sen=>$wire)

Например, демон can_ato_power в котором X должен быть источником, проверяет является ли Y проводом. Демон can_ato_wire проверяет, не присоединяли ли уже X (это провод) к Y (что угодно). Функция .count_in даёт число входящих в узел X рёбер @ato. Если их меньше 2 значит Y можно ещё подключить. В принципе можно было бы взять и .count_out, однако аксиома симметричности (2) поддерживает их число равным (ненаправленное ребро).

При помощи этих демонов, сформулируем "запретительные" аксиомы для ребра @ato конкретных сущностей:

Mind.add(   
   isa(X, Sen=>$wire)  & !can_wire_ato (X,Y) -> !X.@ato.Y,   // (7)
   isa(X, Sen=>$lamp)  & !can_lamp_ato (X,Y) -> !X.@ato.Y,   // (8)
   isa(X, Sen=>$power) & !can_power_ato(X,Y) -> !X.@ato.Y )  // (9)

Целевые аксиомы

Наша задача состоит в выяснении того, горит или нет лампа при данном соединении объектов. Для её решения добавим ещё две аксиомы, которые будут у лампы менять атрибут glow (горит):

Mind.add(
   isa(X, Sen=>$lamp) & isa(Y, Sen=>$power) &  X.@bind.Y ->  X.@attr.Sen=>$glow,   // (10)
   isa(X, Sen=>$lamp) & isa(Y, Sen=>$power) & !X.@bind.Y -> !X.@attr.Sen=>$glow )  // (11)

Смысл их прост. Если X является лампой, а Y - источником и они связаны (непосредственно или через другие объекты), то у лампы атрибут истинный. Если же не связаны, то он ложный.

Ещё одна аксиома проверяет наличие короткого замыкания, при наличии самозамыкания:

Mind.add(
   isa(X, Sen=>$lamp) & isa(Y, Sen=>$power) &  X.@bind.Y &  X.@bind.X ->  X.@attr.Sen=>$break,
  !isa(X, Sen=>$lamp)  -> !X.@attr.Sen=>$glow,                                    // (13)
   X.@attr.Sen=>$break -> !X.@attr.Sen=>$glow )                                   // (14)

Вторая аксиома запрещает гореть не лампе, а третья -- гореть перегоревшей лампочке.

Тестируем простую модель

Протестируем введенные знания. Создадим граф первой задачи G1, сделаем его активным и добавит 5 конкретных сущностей: две лампочки, два провода и источник напряжения.

var G1 = GRAPH("Model1")           // создаём конструктором путой граф
GRAPH = G1                         // делаем его текущим и добавляем узлы
nodes $L1, $L2, $W1, $W2, $P       // 2 лампы, 2 провода и источник

[$L1, $L2].@isa.Sen=>$lamp = True  // сообщаем чьи это экземпляры
[$W1, $W2].@isa.Sen=>$wire = True
$P.@isa.Sen=>$power = True

var G1a = G1.copy();               // сохраняем модель

После объявления узлов (находящихся в сознании системы), они связываются с абстрактными классами графа Sen отношениями @isa. Тем самым указывается их разновидность. Последняя строка сохраняет копию модели, которая в дальнейшем нам пригодится.

Подключим сначала лампу $L1 через провод $W1 к источнику $P и запустим логический вывод:

$W1.@ato.[$L1, $P] = True          // задаём связи

Mind.set_graph(G1)                 // запускаем логический вывод

out $P. @attr.Sen=>$glow           //> False
out $L1.@attr.Sen=>$glow           //> True
out $L2.@attr.Sen=>$glow           //> Undef

Источник питания получил атрибут glow со значением False, так как по аксиоме (13) светиться могут только лампы. Лампа $L1 засветилась (она через провод $W1 связана с источником).

Лампа $L2 вернула неопределённое значение атрибута. Напомним, что в DemonScript, если отношение явным образом не задано, то оно имеет логическое значение Undef. Если аксиомы при логическом выводе его не поменяли, это значит, что оно может быть как истинным, так и ложным (неполнота исходной информации). Попробуем устранить эту неполноту, явным образом указав, что лампа $L2 ни с кем не связана (в силу аксиомы симметричности (2), это достаточно сделать в одну сторону):

for X in True:                     // все узлы графа
   $L2.@ato.X = False              // не присоединены к лампе
   
Mind.set_graph(G1)                 // запускаем логический вывод   

out $L2.@attr.Sen=>$glow           //> False

Теперь, благодаря аксиоме (6) был сделан вывод, что $L2 не связан с P, что по (11) привело к выводу, что лампа не горит.

Вывод всех моделей

Заставим DemonScript построить все разрешённые модели в которых обе лампочки горят. Для этого "сбросим" все соединения, вернувшись к исходной модели, в которой были установлены только @isa отношения. Затем, установим атрибуты горения в True и запустим генератор моделей:

G1 = G1a.copy();

[$L1, $L2].@attr.Sen=>$glow = True

var Models = Mind.get_models(G1, @ato, 100)    // все возможные модели
var I = 0
for M in Models:                               // выводим их
   out M.dot("model"+(I++)+".dot", [@ato], False)     
out "models count: ", Models.size()

Добавляем вилку с розеткой

Добавим теперь вилку с розеткой К вилке fork можно присоединять только один провод и одну розетку. Аналогично к розетке socket - только одну вилку и один провод.

def can_socket_ato(X,Y) :
   return ( ato(X, Y) | X.count_in(@ato) < 2 ) & ( isa(Y, Sen=>$wire) | isa(Y, Sen=>$fork) )
   
def can_fork_ato(X,Y) :
   return ( ato(X, Y) | X.count_in(@ato) < 2 ) & ( isa(Y, Sen=>$wire) | isa(Y, Sen=>$socket) )

К источнику напряжения power можно подключать только провода (в любом количестве).