DemonScript: Мы не двойняшки...
Введение
По мере описания обыденных знаний, число различных отношений быстро растёт. Отношения часто образуют определённую иерархию. Например, отношение mother является подмножеством отношения parent. Однако, когда отношения определяются при помощи рёбер edges, теряется возможность их группировки и иерархического упорядочивания.
В этом документе объясняется как можно работать с произвольными отношениями не вводя для них соответствующих типов рёбер. Описываемый подход применим не только к отношениям, но и к произвольным предикатам: логическим функциям зависящим от n переменных (отношение - это бинарный предикат с n=2).
Вторая важная составляющая обыденных знаний - это атрибуты объектов. Человек может характеризоваться именем, годом рождения, весом и т.п. Ниже мы рассмотрим множество людей и родственные отношения между ними, на примере которых введём узлы атрибутов и отношений.
Определяем абстрактные классы
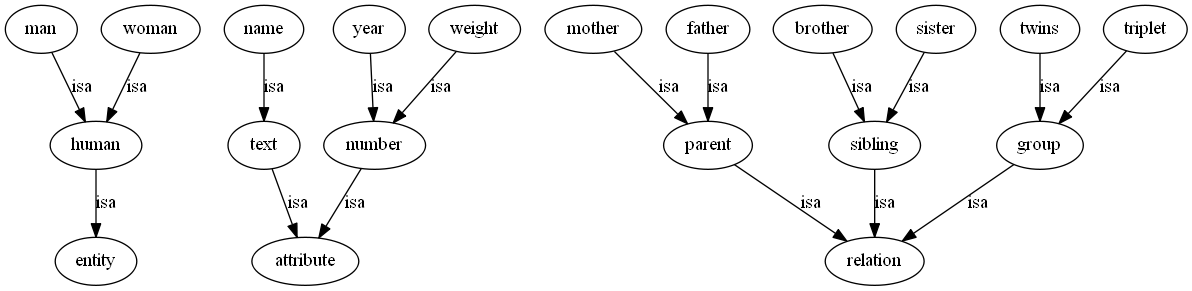
Начнём c определения единственного отношения rel. Оно будет означать, что объект вступает в некоторое отношение с одним или несколькими объектами. Создадим также три графа. В графе Sen будут храниться абстрактные классы. В графах Attr и Rel - вспомогательные узлы для атрибутов и отношений (описаны ниже):
edges rel // тип отношения
var Sen = GRAPH("Sen") // граф с абстрактными классами
var Attr = GRAPH("Attr") // граф с узлами атрибутов
var Rel = GRAPH("Rel") // граф с узлами отношений
global Rel, Sen, Attr // будут доступными в демонах
Перечислим абстрактные классы, разбив их на три группы: entity - то, что можно увидеть (их экземпляры будут реальными объектами), attribute - характеристики объектов и relation - множество отношений, в которые вступают объекты:
GRAPH = Sen // делаем граф Sen текущим
nodes $entity, $attribute, $relation, // добавляем в него узлы
$human, $man, $woman,
$text, $name, $number, $year, $weight,
$parent, $mother, $father, $sibling, $brother, $sister,
$group, $twins, $triplet;
[$human] isa $entity; // определяем иерархию isa
[$man, $woman] isa $human;
[$text, $number] isa $attribute;
[$name] isa $text;
[$year, $weight] isa $number;
[$parent, $sibling] isa $relation;
[$mother, $father] isa $parent;
[$brother,$sister] isa $sibling;
[$group] isa $relation;
[$twins, $triplet] isa $group;
Sen.dot("sen.dot") // выводим граф в файл в dot-формате
Напомним, что отношение X isa Y (X является подмножеством
или экземпляром класса Y) и отношение
X attr Y (X имеет атрибут Y) являются базовыми
и их объявлять не надо.
Сохранение графа Sen в dot-формате, позволяет получить png-файл
со структурой графа. Он выглядит следующим образом:
Задание атрибутов
 Любой узел может хранить одно значение базового типа (число, строка, логическое значение и т.д.)
Чтобы связать с атрибутом его семантику, значение поместим во вспомогательный узел,
который по отношению isa свяжем с одним из абстрактных классов, потомков множества $attribute.
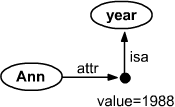
Графически это изображено на рисунке справа. Вспомогательный узел обозначен жирной точкой, рядом с которым
приведено его значение value=1988. Отношением isa он связан с классом
$year графа Sen. В свою очередь, конкретный объект "Ann", связан со вспомогательным узлом
отношением attr. Это означает, что Анна родилась в 1988 году.
Любой узел может хранить одно значение базового типа (число, строка, логическое значение и т.д.)
Чтобы связать с атрибутом его семантику, значение поместим во вспомогательный узел,
который по отношению isa свяжем с одним из абстрактных классов, потомков множества $attribute.
Графически это изображено на рисунке справа. Вспомогательный узел обозначен жирной точкой, рядом с которым
приведено его значение value=1988. Отношением isa он связан с классом
$year графа Sen. В свою очередь, конкретный объект "Ann", связан со вспомогательным узлом
отношением attr. Это означает, что Анна родилась в 1988 году.
Чтобы "не захламлять" граф объектов вспомогательными узлами, они будут храниться в отдельном графе Attr (он объявлен выше).
Определим демона attr, который задаёт и читает атрибут объекта. Это будет выглядить следующим образом:
attr(Sen.$year, Ann) = 1988 // задание атрибута out attr(Sen.$year, Ann) // чтение атрибутаДемон состоит из трёх разделов. Первый раздел выполняется в любом случае. В нём запоминается текущий граф G при входе в демон (к нему относится узел X). Так как демон переопределяет (для цикла for) текущий граф (во второй строке), необходимо явная ссылка на граф к которому относится узел X, что далее в коде делается конструкции G.X. В разделе, идущем после оператора get содержится код чтения значения отношения. В разделе set - записи его значения:
def attr(R, X)
{
var G = GRAPH // X относится к текущему графу
GRAPH = Attr // делаем текущим граф Attr
get: // получаем значение отношения:
for P in G.X attr P :
if P isa R :
return P.value()
set: // устанавливаем значение отношения:
for P in G.X attr P :
if P isa R :
return P.value(value) // изменение значения
var P = Attr.add_node() // добавляем в граф Rel узел P
P isa R; // тип атрибута
G.X attr P; // кто его имеет
return P.value(value) // задаём значение
}
В разделе get, если найден узел P,
то у него вызывается метод .value(), возвращающий текущее
значение, которое хранит узел P.
В разделе set, если аналогичный цикл находит у объекта X
вспомогательный узел, то его значение перезаписывается.
Для этого используется ключевое слово value, хранящее в себе значение которое присваивают в демона.
Если же P не найдено, то создаётся вспомогательный узел, устанавливаются
соответствующие рёбра и присваивается значение value.
Заметим, что секция set также возвращает значение атрибута. Благодаря этому демон может участвовать в цепочке присваиваний: attr(R,X)=attr(R,Y)=1988.
Для удобства работы, можно таккже ввести вспомогательных демонов, задающих год рождения и вес объекта:
def year(X): // год рождения человека X get: return attr(Sen.$year, X) set: return attr(Sen.$year, X) = value def weight(X): // вес в кг человека X get: return attr(Sen.$weight, X) set: return attr(Sen.$weight, X) = value
Тестируем атрибуты
Протестируем введенных демонов. Для этого создадим новый граф G и наполним его несколькими конкретными людьми:
var G = GRAPH("G") // создаём граф при помощи конструктора
GRAPH = G // делаем его текущим
nodes Ann, Jon, Mia, Liz, Mia // добавляем именованные узлы
Зададим атрибуты:
year (Ann) = 1988 // Анна родилась в 1988 году weight(Ann) = 56 // Она весит 56 кг out year (Ann) //> 1988 out weight(Ann) //> 56 out year (Mia) //> Undef
Если вывести графы (out Attr, G), то их структура будет иметь вид:
Attr { G {
1 { val: 1988, isa: [Sen.$year] }, Ann { attr: [Attr.1(1988),Attr.2(56)] },
2 { val: 56, isa: [Sen.$weight] } Mia {},
} }
В DemonScript механизм демона attr является встроенным и имеет следующий синтаксис:
Mia[Sen.$year] = 2003; // задаём значение атрибута out "Mia:", Mia[Sen.$year] // выводим егоВ этом примере вспомогательный узел создаётся в текущем графе людей. Если же он находится в дополнительном графе Attr, пишем:
Mia[Sen.$year, Attr] = 2003; // задаём значение атрибута out "Mia:", Mia[Sen.$year, Attr] // выводим его
Типы отношений
Перейдём к отношениям. Чтобы описать любое число отношений при помощи единственного ребра rel, также необходимо вводить вспомогательные узлы. Для произвольного отношения R(X,Y), объект X устанавливает отношение X rel P, где P - вспомогательный узел. Он, в свою очередь, связан со вторым объектом: P rel Y. Чтобы определить смысл отношения, из P устанавливается isa связь с одиним из абстрактных классов - подмножеств класса relation:

На втором рисунке приведено симметричное бинарное отношение для которого не играет роль порядок аргументов. Примером может служит отношение близнецы(X,Y) Аналогично, на третьем рисунке определяется симметричный предикат от трёх аргументов, например, тройняшки(X,Y,Z). Наконец, на четвёртом рисунке приведена структура трёхместного предиката у которого два из трёх аргументов симметричны, например, между(X, Y, Z) - X находится между Y и Z.
Заметим, что для симметричного предиката с n аргументами при обычном подходе потребовалось бы установить n! рёбер (все возможные перестановки). Теперь же необходимо только n рёбер, направленных во вспомогательный узел.
Как и для атрибутов, вспомогательные узлы отношений будем хранить в отдельном графе Rel. Определим демона rel_bin, который создаёт универсальное бинарное отношение, подобное первому рисунку выше:
def rel_bin(R, X, Y)
{
var G = GRAPH // X,Y относятся к текущему графу
GRAPH = Rel // делаем текущим граф Rel
get: // получаем значение отношения:
for P in G.X rel P :
if (P rel G.Y) & P.isa(R) :
return P.value()
set: // устанавливаем значение отношения:
for P in G.X rel P :
if (P rel G.Y) & (P isa R) :
return P.value(value)
var P = Rel.add_node() // создаём узел
P isa R; // тип отношения
G.X rel P; P rel G.Y; // его 2 аргумента
return P.value(value) // присваиваем в него значение
}
В get-е цикл for и ищет узел P,
связанный с X отношением rel слева и с объектом Y справа.
Кроме этого он должен быть isa типа R.
Если такой узел найден, он возвращает методом .value(), хранящееся в нём значение
(оно будет всегда логическим).
Вместо прямого ребра P isa R используется функция P.isa(R),
обеспечивающая наследование отношений.
В принципе, все три условия можно было бы поместить в цикл: for P in (X rel P) & (P rel Y) & (P isa R). Однако тогда он работал бы медленнее. Дело в том, что для простого условия типа for P in X rel P перебираются только входящие в узел рёбра (как здесь) или выходящие из узла рёбра. Это достаточно быстрая операция. Для составного условия происходит перебор всех узлов графа, чтобы выяснить истинность условия.
В разделе set происходят сначала аналогичные действия и, если узел P найден, в нём сохраняется присваиваемое в демон значение value. Если же такого узла не нашлось, то он создаётся в графе Rel
При помощи демона произвольного бинарного отношения, можно для краткости определить демоны конкретных отношений. Например, для матери и родителя имеем:
def mother(X, Y): // X является матерью Y get: return rel_bin(Sen.$mother, X, Y) set: return rel_bin(Sen.$mother, X, Y) = value def parent(X, Y): // X является родителем Y get: return rel_bin(Sen.$parent, X, Y) set: return rel_bin(Sen.$parent, X, Y) = value
Тестируем демонов отношений
Протестируем этих демонов. По-прежнему будем использовать граф G с людьми: Определим двух матерей:
mother(Ann, Liz) = mother(Liz, Mia) = True
Выведем значения отношений:
out mother(Ann, Liz) //> True out mother(Liz, Mia) //> True out mother(Liz, Mia) //> Undef out parent(Ann, Liz) //> TrueКак видно, в качестве бесплатного приложения, мы автоматически получили верное значение демона parent. В демоне rel_bin, в циклах была использована функция P.isa(R), которая возвращает True, если при перемещении по рёбрам isa от узла P будет найден узел R. Благодаря тому, что $mother isa $parent, демон parent делает правильный "вывод" из фактов с матерями.
Имеет смысл проанализировать структуру графов, после введения в них фактов:
Rel { G {
1 (True){ Ann { rel: [Rel.2(True)] },
isa: [Sen.$mother], Mia {},
rel: [G.Mia], Jon {},
}, Liz { rel: [Rel.1(True)] },
2 (True){ Mia {}
isa: [Sen.$mother], }
rel: [G.Liz],
}
}
Симметричные отношения
Определим теперь демона rel_sym, который реализует симметричное отношение с произвольным числом аргументов. Их будем передавать через массив Objs. В общей секции происходит поиск вспомогательного узла P, связанного по isa с классом R. С этим узлом должны быть связаны все объекты из массива Objs. Это не самое эффективное, но наиболее простое решение:
def rel_sym(R, Objs)
{
var G = GRAPH // Objs относятся к текущему графу
GRAPH = Rel // делаем текущим граф Rel
var Ok = False, PN // если нашли, запомним в PN и Ok == True
for P in P isa R { // по отношениям нужного типа
Ok = True // все ли объекты из Objs
for Ob in Objs : // указывают на узел P?
if (G.Ob rel P) != True{Ok=False; break} // если не все, прерываемся
if Ok { PN = P; break } // все указывают - это нужное отношение
}
get: // получаем значение отношения:
if Ok : return PN.value()
set: // устанавливаем значение отношения:
if Ok : return PN.value(value)
var P = Rel.add_node() // добавляем в граф Rel узел P
P isa R = True // связываем его с классом отношения
for Ob in Objs : // каждый объект из массива Objs
G.Ob rel P; // указывает на вспомогательное значение
return P.value(value) // задаём логическое значение
}
При помощи помощи этого демона определим предикаты близняшек и тройняшек:
def twins(X,Y): // X и Y близнецы get: return rel_sym(Sen.$twins, [X, Y]) set: return rel_sym(Sen.$twins, [X, Y]) = value def triplet(X,Y,Z): // X,Y,Z - тройняшки get: return rel_sym(Sen.$triplet, [X, Y, Z]) set: return rel_sym(Sen.$triplet, [X, Y, Z]) = valueПротестируем этих демонов:
G.clear_edges(); Rel.clear_edges() // очищаем рёбра triplet(Mia, Mia, Jon) = True // задаём отношение out "triplet:",triplet(Mia, Mia, Jon) //> True out "triplet:",triplet(Mia, Mia, Ann) //> Undef
Эмулируем Mind
Как работать с введенными демонами в объекте логических выводов Mind, мы рассмотрим в другом документе. Сейчас "сэмулируем" его работу, задав два правила: 1) если три человека попарно близняшки, то они и тройняшки; 2) если три человека тройняшки, то они попарно и двойняшки:
def micro_mind(G)
{
GRAPH = G
for X {
for Y {
if X==Y : continue
for Z {
if Z==X | Z==Y: continue
if twins(X,Z) & twins(Z,Y) : triplet(X,Y,Z) = True // правило 1)
if triplet(X,Y,Z) : twins(X, Y) = True // правило 2)
}
}
}
}
Так как нельзя быть самому себе близнецом, в циклам X,Y,Z стоят проверки
того, что это различные объекты.
Протестируем этот "движок логического вывода":
Rel = GRAPH("Rel") // полностью обнуляем граф
G.clear_edges(); // очищаем рёбра
GRAPH = G
triplet(Ann, Mia, Mia) = True // объявляем их тройняшками
micro_mind(G); // запускаем логический вывод
out "tw",twins(Ann, Mia) //> True
out "tw",twins(Ann, Mia) //> True
out "tw",twins(Mia, Mia) //> True
out "tw",twins(Mia, Liz) //> Undef
out "tr",triplet(Ann, Mia, Liz) //> Undef
Полный код этого примера находится в файле demon_set.ds.
Связь атрибутов
Часто информация о значениях атрибутов поступает опосредованным образом. Например, известно, что Лиза старше Анны на 5 лет, однако годы их рождения неизвестны. Тем не менее, эту информацию необходимо сохранить, с тем, чтобы, когда станет известным год рождения любой из них, получить год рождения другой. Для этого можно ввести новый класс отношений delta (подмножество класса number). На первом рисунке ниже показано как соответствующий вспомогательный узел соединяется со вспомогательными узлами атрибутов:

Атрибут delta хранит в себе значение разницы 5 между годами рождения объектов. Последние пока имеют неопределённые (Undef) значения. Когда становится известен возраст Анны, система автоматически выводит возраст Лизы (рисунки справа). Правила вывода задаются аксиомами и применимы к любым классам, наследникам множества number (в том числе и к самому отношению delta).
В ряде случаев, атрибут delta возникает при логическом выводе различных предикатов. Например, известно, что родители старше детей. Поэтому, если установлена истинность отношения parent(X,Y), из него следует связь delta между атрибутами $year у объектов X и Y. При этом, из базы знаний может быть извлечена типичная разница в виде нечёткого числа, например (16, 25, 60), что означает треугольное распределение с максимумом в 25 и границами от 16 до 60 лет. Соответственно, если становится известным год рождения, например, родителя, то это даёт диапазон возможных годов рождения ребёнка.