Импликация и логическое следование
Импликация
Ещё одна важная связка \(A\to B\), называется импликацией. Она ложна только для комбинации \(\T\to \F\), что интерпретируется как "из истины нельзя получить ложь". В остальных случаях она истинна:
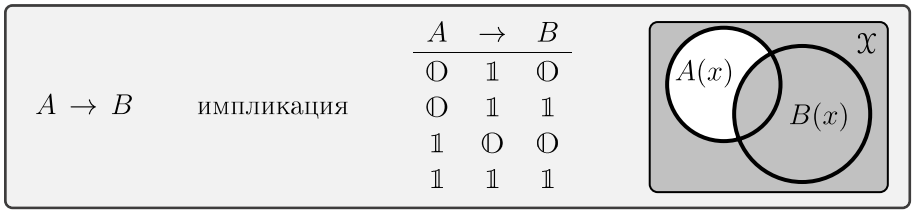
Из истины "следует" истина, поэтому \(\T \to \T\) это \(\T\). Из лжи можно вывести что угодно, поэтому \(\F \to \F\) и \(\F \to \T\) считаются истинными. Аргументы импликации называются посылкой и следствием.
Для высказываний интерпретация импликации, как логического следования выглядит
странной.
Так \((2\cdot 2=4) ~\to~~\)
"Солнце это звезда" — истинная формула, хотя
посылка и следствие между собой ни как не связаны.
Лучше ситуация для предикатов. Например, в арифметике при любом \(x\) истинно утверждение: "если \(x < 2\), то \(x < 4\)", или \((x < 2) \to (x < 4)\). Когда посылка истинна (\(x=1\)), истинно и следствие. Если же посылка ложна, то следствие может быть как истинным (при \(x=3\)), так и ложным (при \(x=5\)). Эти случаи соответствуют строчкам таблицы истинности, где стоит \(\T\). "Менее правильное" утверждение \((x > 2) \to (x < 4)\) ложно при \(x=5\).
Стоит графически проверить, что если область истинности предиката \(A(x)\) является подмножеством \(B(x)\), то их импликация \(A(x)\to B(x)\) всегда истинна и наоборот. Так обстоит дело для "\((x<2) \to (x<4)\)". Именно в этом случае функция импликации имеет смысл следования.
При помощи таблиц истинности несложно показать, что импликация выражается через остальные логические связки (приоритет "\(\to\)" считаем большим, чем у "\(\equiv\)" и меньшим, чем у "\(\vee,~\&~\neg\)" ): \[ A \to B~ \equiv~ \neg A \vee B. \] В свою очередь, эквивалентность \(A \equiv B\) имеет такую же таблицу истинности, как и \((A\to B) \,\&\, (B\to A)\), что интерпретируется как следование в обе стороны. В частности формула \[ (A \equiv B) \equiv (A\to B) \,\&\, (B\to A) \] всегда истинная (общезначимая), т.е. она является тавтологией.
Логическое следование
Пусть \(P=P(A,B(x),...)\) и \(Q=Q(A,C(x,y),...)\) формулы, зависящие от высказываний и предикатов. Эти формулы равны \(\T\) или \(\F\) при определённых значениях, входящих в них элементарных утверждений.
Например: \[ A ~\Rightarrow~ A\vee B,~~~~~~~~~~~~~~~~A\,\&\,B ~\Rightarrow~ A. \] Так, первое следование означает, что если \(A\) истинно, то для любого \(B\), дизъюнкция \(A\vee B\) будет истинной. Справедлива теорема:
Например, формула \(A \to (A\vee B)\) — общезначима. Импликация \(P\to Q\) (бинарная функция), в отличие от следования \(P\Rightarrow Q\), определена и когда \(P\) ложно. При логическом же следовании подразумевается истинность посылки. В частности, справедливо правило modus ponens:
\[ ({\bf MP})~~~~~~~~~~~~~~~P ,~~~ P \to Q ~~~~~\Rightarrow~~~~~Q. \]означающее, что если обе посылки \(P\) и \(P\to Q\) истинны, то истинна и формула \(Q\). Если \(P\equiv\F\), то \(Q\) — это \(\T\) или \(\F\). Стоит проверить общезначимость формулы \(P\,\&\,(P\to Q) \to Q\).
Следствие обладает транзитивностью: \[если~P\Rightarrow X~ и~X\Rightarrow Q,~то~P\Rightarrow Q.\]
Следствие в общем случае не симметрично. Так, \(A ~\Rightarrow~ A\vee B\) ( справедливо только в одну сторону и из \(A\vee B\) не следует \(A\) (поэтому \(A\vee B \to A\) не тавтология. Тем не менее, существуют и следования в обе стороны: \(\Leftrightarrow\). Например: \(A\vee B ~\Leftrightarrow B\vee A\) или двухстороннее правило: \[ A\,\&\, B ~\Leftrightarrow A,~~ B. \] Вправо, это \(A\,\&\, B\Rightarrow A\), влево оно означает: когда обе посылки \(A\) и \(B\) истинны, истинна и их конъюнкция.
Двухсторонний вывод \(P\Leftrightarrow Q\)
аналогичен функции эквивалентности \(P\equiv Q\).
Утверждения: "если \(P\), то \(Q\) и наоборот", "\(P\) тогда и только тогда, когда \(Q\)"
означают \(P\Leftrightarrow Q\).
Если \(P\Rightarrow X\Rightarrow Q\), то \(P\) называют достаточным условием, а \(Q\) — необходимым условием для \(X\). Когда необходимое и достаточное условия совпадают, то они совпадают и с \(X\): \(P\equiv Q\equiv X\).
Прямой логический вывод
Большинство рассуждений в математике можно разделить на прямые и обратные. Получение по \((\bf MP)\) из двух формул \(P\) и \(P\to Q\) третей формулы \(Q\) является примером прямого логического следования. Ещё одно, более мощное, правило прямого следования называется резолюцией: \[ ({\bf Res})~~~~~~~~~~~~~~~P\vee S ,~~~ \neg P \vee Q ~~~~~\Rightarrow~~~~~S\vee Q. \] Действительно: так как \(P\) и \(\neg P\) не могут быть одновременно истинными, а посылки \(P \vee\, S\) и \(\neg P\vee Q \) истинны по определению, то истинно \(S\) или \(Q\). Если \(S\) — ложно, получается частный случай \(({\bf MP})\). Стоит также проверить, что \((P\vee S) \,\&\,(\neg P \vee Q) ~\to~S\vee Q\) — это тавтология.
Вариантом резолюции является метод цепочек импликаций: \[ P\to S,~~~S\to Q ~~~~~\Rightarrow~~~~~ P\to Q. \] Если в каждой формуле выразить импликацию через дизъюнкцию (заменить \(P\to S\) на \(\neg P\vee S\)), то получится следование, совпадающее с резолюцией точностью до переобозначений: \[\neg P \vee \underline{S},~~\neg \underline{S} \vee Q~~\overset{\bf Res}{\Rightarrow}~~ \neg P\vee Q\].
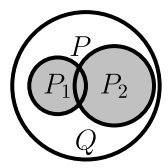Метод разбора случаев — ещё один пример прямых рассуждений.
Пусть из \(P\) необходимо вывести \(Q\).
Рассмотрим несколько утверждений, например, \(P_1\)
и \(P_2\), объединение которых равно \(P\).
Говорят, что \(P_1\) и \(P_2\) покрывают все возможные случаи.
Если из каждого утверждения \(P_i\) следует \(Q\), то оно следует и из \(P=P_1\vee P_2\):
\[
P_1\vee P_2,~~~P_1\to Q,~~~P_2\to Q ~~~~~\Rightarrow~~~~Q.
\]
\(\lhd\)
Докажем это правило при помощи резолюции:
\[
\underline{P_1}\vee P_2,~~~\neg \underline{P_1}\vee Q,~~~\neg P_2\vee Q ~~~~~\overset{\bf Res}{\Rightarrow}~~~~~~
\underline{\underline{P_2}}\vee Q,~~~\neg \underline{\underline{P_2}}\vee Q~~~~~\overset{\bf Res}{\Rightarrow}~~~~Q.
\]
Формула и её отрицание подчёркнуты. В первом выводе это \(P_1\)
и из формул \(P_1\vee P_2\)
и \(\neg P_1\vee Q\)
следует \(P_2\vee Q\).
Во втором выводе формула и её отрицание — это \(P_2\), а резолюция приводит к \(Q\vee Q~\Leftrightarrow~ Q\). \(\square\)
Приведём в качестве неформального примера простую теорему:
По определению \(\mathrm{Even}(x)\) и \(P_1\), существуют такие \(n,m\in \mathbb N\), что \(x=2n\) и \(y=2m\). Тогда \(x+y=2(n+m)\) — чётно (\(Q\)).
Во втором случае \(P_2:\) \(x=2n+1\), \(y=2m+1\) и \(x+y=2(n+m+1)\) также чётно (снова \(Q\)). Поэтому теорема истинна. \(\square\)
Доказательство от противного
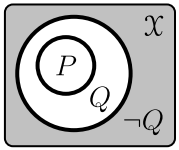
Доказательство от противного — исключительно важный обратный метод. В нём, вместо прямого заключения \(P ~\Rightarrow~ Q\), показывают, что \(P\) и отрицание \(Q\) противоречивы, т.е. из них следует всегда ложное утверждение, подобное \(A\,\&\,\neg A\equiv \F\):
\[ P~\&~\neg Q ~\to~~\F~~~~~~~~~\Leftrightarrow~~~~~~~~~~P ~\to~ Q. \] На рисунке область истинности формулы \(P\) является подмножеством области истинности \(Q\), поэтому отрицание \(Q\) (серый цвет) и \(P\) не пересекаются (\(P\,\&\,\neg Q\equiv \F\)). Несложно видеть, что \(\neg (P\, \&\, \neg Q) ~\equiv~ P\to Q\). Дадим также формальное доказательство метода от противного.
\(\lhd\) Пусть \(P\,\&\,\neg Q~\to~\F\) истинно. Тогда по определению импликации \(P\,\&\,\neg Q\) ложно. Для \(\{P,\,Q\}\) возможно 3 варианта \(\{\F,\,\F\}\), \(\{\F,\,\T\}\) и \(\{\T,\,\T\}\). Для всех них \(P\to Q\) истинно. Аналогично для логического следования в обратную сторону. \(\square\)
Доказательство от противного это очень мощный метод. Существует множество математических утверждений, для которых известно только доказательство от противного.
Косвенное доказательство — это частный случай метода от противного. В нём, вместо \(P \to Q\), выясняется, что \(\neg Q \to \neg P\). Если это так, то значит справедливо и \(P \to Q\): \[ \neg Q ~\to~ \neg P ~~~~~~~~~\Leftrightarrow~~~~~~~~~~P ~\to~ Q. \] Фактически \(\neg Q\to \neg P\) равно \(Q\vee \neg P\), что эквивалентно \(P\to Q\).
Подобный метод вывода может показаться тривиальной тавтологией. Однако это не так. На практике берут отрицание \(\neg Q\). Из этой формулы логически выводят (иногда довольно сложным образом) формулу \(\neg P\). Если построен вывод \(\neg Q~\Rightarrow~\neg P\), то, как мы видели выше, формула \(\neg Q\to \neg P\) оказывается тавтологией. Именно на этом этапе, при помощи косвенного доказательства, выводится \(P\to Q\). Наконец, если посылка \(P\) считается истинной, то по правилу \(({\bf MP})\) из \(P\) и \(P\to Q\) выводится \(Q\).
Классический пример рассуждения от противного, доказательство, что
\(\lhd\)
В качестве \(P\) выступают стандартные аксиомы арифметики.
Необходимо доказать \(Q:~\sqrt{2}\neq n/m\), где \(n/m\) несократимая дробь.
Пусть \(\neg Q: ~\sqrt{2}=n/m\). Тогда \(n^2=2m^2\)
и следовательно \(n\) — чётно, т.е. \(n=2k\).
Но тогда \((2k)^2 = 2m^2\) или \(m^2 = 2k^2\), т.е. \(m\) — также чётно,
а это противоречит несократимости дроби \(n/m\).
Поэтому \(Q\) истинно. \(\square\)