REF: Matplotlib
Introduction
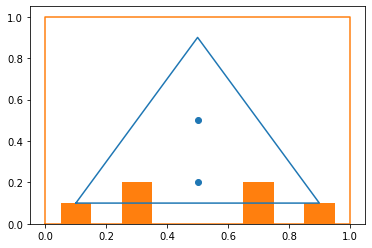
import matplotlib.pyplot as plt plt.plot ((0.1, 0.5, 0.9, 0.1), (0.1, 0.9, 0.1, 0.1)) plt.plot ((0, 0, 1, 1, 0), (0, 1, 1, 0, 0)) plt.scatter( [0.5, 0.5], [0.2, 0.5]) plt.bar ([0.1,0.3,0.7, 0.9], [0.1,0.2,0.2,0.1], width=0.1) plt.show()In the simplest case, you can create a figure and a coordinate system as follows:
fig = plt.figure() ax = plt.axes()You can plot directly on plt or on the axes
x = np.linspace(0, 10, 1000) ax.plot(x, np.sin(x))
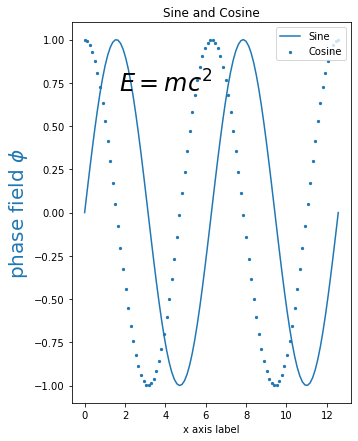
Setting the facecolor (white) allows copying from the notebook without "losing" the axis labels.
plt.figure(figsize=(8,4), facecolor ='w')
plt.plot (x, np.sin(x))
plt.scatter (x, np.cos(x), s=5)
plt.xlabel('x axis label')
plt.ylabel(r'phase field $\phi$',
{'color': 'C0', 'fontsize': 20})
plt.title ('Sine and Cosine')
plt.legend(['Sine', 'Cosine'])
plt.text(4, 0.75, r'$E=mc^2$',
{'color': 'black', 'fontsize': 24,
'ha': 'center', 'va': 'center'})
plt.show()
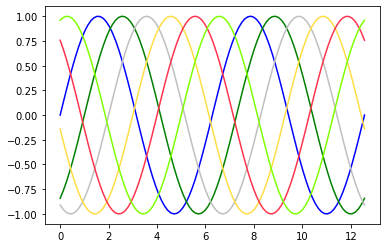
Colors and line style
x = np.linspace(0, 4*np.pi, 100) plt.plot(x, np.sin(x - 0), color='blue') plt.plot(x, np.sin(x - 1), color='g') plt.plot(x, np.sin(x - 2), color='0.75') plt.plot(x, np.sin(x - 3), color='#FFDD44') plt.plot(x, np.sin(x - 4), color=(1.0,0.2,0.3)) plt.plot(x, np.sin(x - 5), color='chartreuse')
plt.plot(x, x + 0, '-g') # solid green plt.plot(x, x + 1, '--c') # dashed cyan plt.plot(x, x + 2, '-.k') # dashdot black plt.plot(x, x + 3, ':r'); # dotted red plt.plot(x, x + 4, linestyle='-') # solid plt.plot(x, x + 5, linestyle='--') # dashed plt.plot(x, x + 6, linestyle='-.') # dashdot plt.plot(x, x + 7, linestyle=':') # dotted

x = np.zeros(8)
fig, ax = plt.subplots()
ax.plot(np.arange(-1, 7),
color=(0.1,0.2,0.9,0.5),
linewidth=12)
ax.plot(x, color=(0.9,0.2,0.9))# RGB
ax.plot(x+1, color='#0a0b0c') # hex RGB
ax.plot(x+2, color='#0a0b0c3a') # hex RGBA
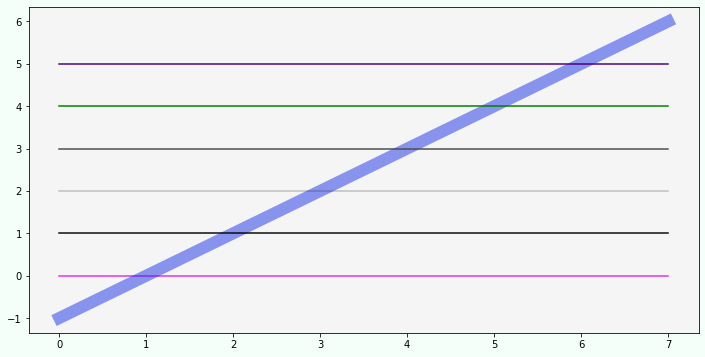
ax.plot(x+3, color='0.3') # gray level
ax.plot(x+4, color='g') # b,g,r,c,m,y,k,w
ax.plot(x+5, color='indigo') # name from X11/CSS4
fig.set_figwidth(12)
fig.set_figheight(6)
fig.set_facecolor('mintcream')
ax.set_facecolor('whitesmoke')
plt.show()
Axes and scale
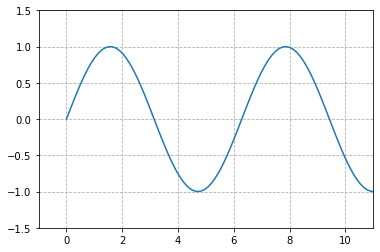
plt.plot(x, np.sin(x)) plt.xlim(-1, 11) plt.ylim(-1.5, 1.5); plt.grid(True, linestyle='--')
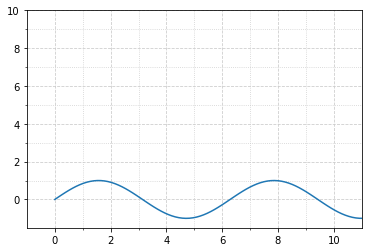
ax = plt.figure().add_subplot(1, 1, 1) plt.plot(x, np.sin(x)) plt.axis([-1, 11, -1.5, 1.5]) # [xmin, xmax, ymin, ymax] majors, minors = np.arange(0,11,2), np.arange(0,11,1) ax.set_xticks(majors); ax.set_xticks(minors, minor=True) ax.set_yticks(majors); ax.set_yticks(minors, minor=True) ax.grid(which='major', color='#CCCCCC', linestyle='--') ax.grid(which='minor', color='#CCCCCC', linestyle=':')
plt.plot(x, np.sin(x))
plt.axis('tight'); # all points will fit
plt.plot(x, np.sin(x))
plt.axis('equal') # equal scale for both x and y
ax = plt.axes()
ax.plot(x, np.sin(x))
ax.set(xlim=(0, 10), ylim=(-2, 2), xlabel='x', ylabel='sin(x)', title='A Plot')
Combining plots
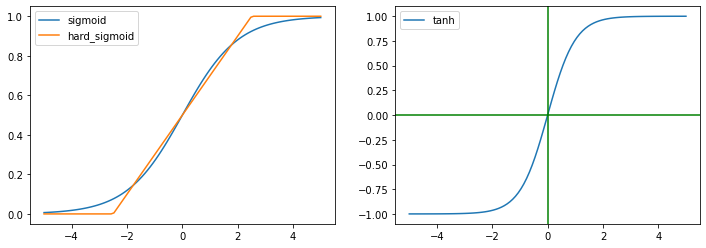
x = np.linspace(-5,5, 100)
y = np.where(x < -2.5, 0,
np.where(x < 2.5, 0.2*x+0.5, 1))
plt.figure(figsize=(12,4))
plt.subplot(1, 2, 1)
plt.plot(x,1/(1+np.exp(-x)))
plt.plot(x,y)
plt.legend(['sigmoid', 'hard_sigmoid'])
plt.subplot(1, 2, 2)
plt.plot(x, np.tanh(x))
plt.axvline(0, c="g")
plt.axhline(0, c="g")
plt.legend(['tanh'])
plt.show()
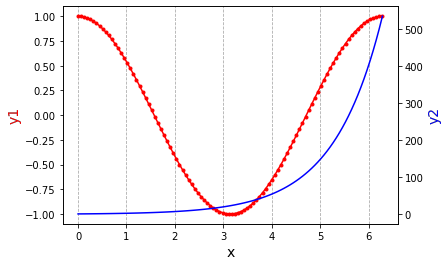
x = np.linspace(0,2*np.pi,100)
y1, y2 = np.cos(x), np.exp(x)
fig,ax = plt.subplots()
plt.grid(axis = 'x', color='#AAA', linestyle='--')
ax.plot(x, y1, color="red", marker=".")
ax.set_xlabel("x", fontsize = 14)
ax.set_ylabel("y1", color="red", fontsize=14)
ax2=ax.twinx()
ax2.plot(x, y2, color="blue")
ax2.set_ylabel("y2",color="blue",fontsize=14)
Scatter plots
np.random.seed(1)
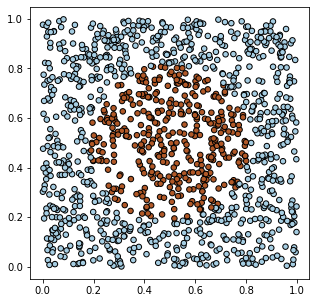
x_dat = np.random.rand(1200, 2)
y_dat = np.sum((x_dat-0.5)**2, axis=1) < 0.1
plt.figure (figsize=(5, 5))
plt.scatter(x_dat[:,0], x_dat[:,1],
s=30, c=y_dat, cmap=plt.cm.Paired, edgecolors='k')
plt.show()
Histograms
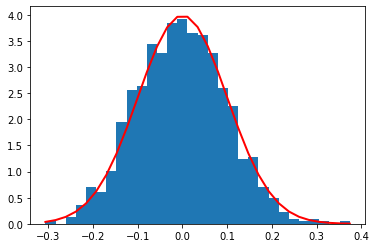
mu, sigma = 0, 0.1
s = np.random.normal(mu, sigma, 1000)
count, bins, ignored = plt.hist(s, 30, density=True)
plt.plot(bins,
1/(sigma*np.sqrt(2*np.pi)) * \
np.exp(- (bins-mu)**2/(2*sigma**2) ),
linewidth=2, color='r')
plt.show()
Height maps
X_MIN, X_MAX, DX, Y_MIN, Y_MAX, DY = 0,1,0.01, 0,1,0.01 x = np.arange(X_MIN, X_MAX+DX, DX) y = np.arange(Y_MIN, Y_MAX+DX, DX) X, Y = np.meshgrid(x, y) # 2D arrays Z = np.maximum(X,Y) # height values plt.figure(figsize=(5,4)) # image size (with color bar)
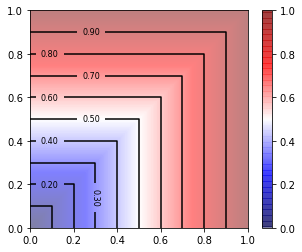
plt.imshow(Z, extent=[X_MIN, X_MAX, Y_MIN, Y_MAX],
origin='lower', cmap='seismic', alpha=0.5) # as a semi-transparent image
plt.colorbar() # color bar on the right
contours = plt.contour(X, Y, Z, 11, colors='black') # contour lines
plt.clabel(contours, inline=True, fontsize=8, fmt='%1.2f') # with height labels
plt.show()
3D plots
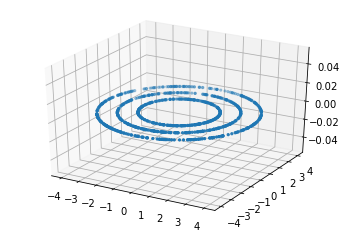
from mpl_toolkits.mplot3d import Axes3D N1 = 1000 phi = 2*np.pi*np.random.random((N1,)) r = np.random.randint(2,5,(N1,)) X = np.zeros((N1,3)) X[:,0] = r*np.cos(phi) X[:,1] = r*np.sin(phi) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.scatter(X[:,0], X[:,1], X[:,2], s=5) plt.show()
Displaying images
from keras.datasets import mnist
# load mnist dataset
(x_train, y_train), (x_test, y_test) = mnist.load_data()
plt.figure(figsize=(5, 4)) # plot the 20 mnist digits
for i in range(20):
plt.subplot(4, 5, i + 1)
plt.imshow(x_train[i,:,:], cmap='gray')
plt.axis('off')
plt.show()

Saving to file
x = np.linspace(0, 10, 100)
fig = plt.figure()
plt.plot(x, np.sin(x), '-')
fig.savefig('my_figure.png')
Information
$$ P(x,y)\,dx\,dy = \exp\Bigr\{-\frac{x^2+y^2}{2\sigma^2}\Bigr\}\,\frac{dx\,dy}{2\pi\sigma^2} = \exp\Bigr\{-\frac{r^2}{2\sigma^2}\Bigr\}\,\frac{2\pi\, r\, dr}{2\pi\sigma^2} ~=~ \Bigr[ z ~=~ \frac{r^2}{2\sigma^2}\Bigr] = e^{-z}\, dz $$