ML: Логика и вероятность. Часть I

Введение

Способность к логическим рассуждениям в условиях неопределённости является важной составляющей любого интеллектуального агента. При помощи теории вероятностей можно обобщить бинарную логику на случай вероятностных моделей, что будет продемонстрировано в следующих статьях. Перед чтением полезно ознакомиться с введением в логику, краткому напоминанию которой и посвещён этот документ.

Теория про Алису и Боба

Алиса и Боб живут в доме, где у каждого есть своя спальня и общая гостиная. Гостей они не принимают. В спальне разрешено находится только её владельцу, а в гостинной могут собираться оба жильца. Известно, что в гостиной кто-то есть и Алиса у себя в спальне. Необходимо прийти к выводу, что в гостиной находится Боб.

Утверждения теории будем записывать при помощи логического отрицания $\bar{A}$ (не $A$), конъюнкции $A\,\&\,B$ (логического И), дизъюнкции $A\vee B$ (логического ИЛИ) и импликации $P\to Q$, сокращающей фразу "если $P$, то $Q$". Напомним, что, если $\T$ - это истинное утверждение, а $\F$ - ложное, то для любого высказывания $P$: $$ \left\{ \begin{array}{lcl} \T~\,\&\,P & \equiv & P\\ \F~\&\,P &\equiv & \F \end{array} \right. ~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} \F\,\vee P &\equiv & P\\ \T\,\,\vee P & \equiv & \T \end{array} \right. ~~~~~~~~~~~~~~~ \left\{ \begin{array}{lclcl} \T\,\to \F &\equiv& \F\\ \T\,\to \T &\equiv& \F\,\to P &\equiv& \T, \end{array} \right. $$ где $\T\,\&\,P \equiv P$ при $P\equiv \F$ и $P\equiv \T$ соответствует $\T\,\&\,\F \equiv \F$ (истина и ложь - это ложь) и $\T\,\&\,\T \equiv \T$. Таким образом, эти формулы являются краткой записью таблиц истинности для логических бинарных операций $\&,~\vee,~\to$.

Обозначим через $A$ высказывание: "Алиса у себя в спальне", через $B$ - "Боб у себя в спальне" и $L$ - "кто-то один из них или оба находятся в гостиной". В качестве аксиом, описывающих этот мир, выберем следующие факты:

Исходные посылки: $L$ (кто-то в гостиной), $A$ (Алиса в спальне) и аксиома $\mathbf{A_1}$ позволяют сделать необходимый вывод, который состоит из трёх шагов: $$ \begin{array}{llclll} 1. & L,~~~~L\to \bar{A}\vee \bar{B} & \Rightarrow & \bar{A}\vee \bar{B} & ~~~~~~~~~~~& L,\mathbf{A_1},~(\text{MP})\\ 2. & \bar{A}\vee \bar{B} & \Leftrightarrow & A \to \bar{B} & & 1,~\text{def}\\ 3. & A,~~~~A \to \bar{B} & \Rightarrow & \bar{B} & & A,2,~(\text{MP}) \end{array} $$ На первом шаге применено правило логического вывода modus ponens (MP): $$ P,~~P\to Q~~~~\Rightarrow~~~~Q. $$ Это правило звучит так: "если истинна формула $P$ и из $P$ следует формула $Q$, то истинна и $Q$". Его справедливость связана со свойством импликации, которая ложна только для $\T\to \F~~$ ("из истины $\T $ нельзя получить ложь $\F $"). Поэтому, если $P~\equiv~\T$ и $P\to Q~\equiv~\T $, т.е. $\T\to Q~\equiv~\T $, то для $Q$ возможно только: $Q\equiv~\T $.
На втором шаге вывода учтена запись импликации через дизъюнкцию. Это также правило вывода (получения новой формулы). В отличии от modus ponens, оно двустороннее: $~~P\to Q~~~\Rightarrow~~~\bar{P}\vee Q~~$ и $~~\bar{P}\vee Q~~~\Rightarrow~~~P\to Q$.
В конце снова использован (MP). Таким образом, при помощи формальных действий с символами, мы приходим к правильному выводу о том, что $\bar{B}$: "Боб не находится у себя в спальне". Для этого нам понадобилась только первая аксиома, тем не менее все три аксиомы являются независимыми и необходимы для описания этого мира.

Теории предикатов первого порядка

В неформальных теориях мы используем естественный язык для описания объектов и их свойств. При этом неизбежны неоднозначности, присущие нашему мышлению. Формализация предметной теории означает запись всех её утверждений в виде формул при помощи однозначных символов. Получение одних утверждений из других производится по также однозначным правилам. В результате синтаксис теории (её форма) отрывается от семантики (содержания) и никакие "очевидности" неявно привнесены быть не могут. Логический вывод такой теории может проверить, например, компьютер, ничего не знающий о смысле её символов.

Построение формальной предметной теории начинается с её сигнатуры, в которой перечисляются типы предметов, константы, функции и предикаты. Типы предметов определяются множествами сущностей с которыми будет оперировать теория. В арифметике это множество чисел, а в планиметрии - два множества: точки $x,y,...\in \mathcal{P}$ и прямые $\alpha,\beta,...\in \mathcal{L}$. Часть сущностей могут объявляться выделенными предметными константами (например, $0$ в арифметике). В сигнатуре теории возможны также предметные функции $f(x)$, $g(x,y)$, $h(x,y,z)$,..., ставящие в соответствие одним предметам - другие (например, $\text{sum}(x,y)$ или кратко $x+y$ в арифметике). Константы, переменные и функции называются термами. Пример терма: $h(0,x,g(x,y))+f(z)$.

Важной и обязательной частью сигнатуры являются предикаты - логические функции, зависящие от предметных величин: $A(x)$, $B(x,y)$,.... и принимающие значения истины $\T $ или лжи $\F $. Логические высказывания, подобные $A,B,L$, рассмотренные в предыдущем разделе, это частные случаи константных предикатов без аргументов.
Свойство - предикат с одним аргументом $A(x)$. Он задаёт некоторое подмножество $\{x\,|\,A(x)\}\subseteq\mathcal{X}$ предметов.
Отношение - предикат $R(x,y)$ с двумя аргументами. Их часто записывают в операционном виде $(x\, R\, y)$.
В арифметике предикатами являются: равенство чисел $x=y$ и их порядок $x\lt y$. В обыденных знаниях, например, $\text{Mather}(x,y):$ "некто $x$ является матерью $y$" или $(x~\text{in}~y):$ "объект $x$ находится внутри объекта $y$".

После фиксирования сигнатуры, записывается набор формул, которые определяют свойства констант, функций и предикатов. Эти формулы называются предметными аксиомами. Кроме них существуют общелогические аксиомы, применимые к любым предметным теориям и правила вывода (способы получения новых формул).

Булева алгебра

При записи утверждений теории (аксиом и теорем), кроме символов сигнатуры участвуют логические связки: отрицание $\neg A$ или кратко $\bar{A}$ (не $A$, $A$ - неверно), дизъюнкция $A\vee B$ (истинно или $A$, или $B$, или оба) и конъюнкция $A\,\&\,B$ (истинно и $A$, и $B$). Дизъюнкция и конъюнкция обладают "обычными" свойствами коммутативности и ассоциативности, подобно сложению или умножению. Между собой они связаны законами дистрибутивности и правилами де-Моргана:

$$ \left\{ \begin{array}{lcl} A\,\&\,(B\vee C) &\leftrightarrow& (A\,\&\,B)\vee (A\,\&\,C)\\ A\vee(B\,\&\, C) &\leftrightarrow& (A\vee B)\,\&\, (A\vee C) \end{array} \right. ~~~~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} \neg(A\,\&\,B) &\leftrightarrow& \neg A\vee \neg B \\ \neg(A\vee B) &\leftrightarrow& \neg A\,\&\, \neg B \end{array} \right. $$ Стрелка в обе стороны $A\leftrightarrow B$ (или что тоже $A\equiv B$) обозначает булеву операцию логической эквивалентности, которая истинна только при совпадении значений аргументов. Например, $\T\leftrightarrow \T$ равно $\T,~~$ а $~~\F\leftrightarrow \T$ равно $\F$.
Эта операция выражается через импликацию, а импликация, в свою очередь, выражается через дизъюнкцию: $$ A\leftrightarrow B ~~~~~\Leftrightarrow ~~~~~(A\to B)\,\&\,(B\to A), ~~~~~~~~~~~~~~~~~~~~~~~~ A\to B ~~~~~\Leftrightarrow ~~~~~\neg A\vee B. $$ Двойная стрелка $\Leftrightarrow$ обозначает заменяемость одной формулы на другую и наоборот. Это возможно, т.к. при любых фиксированных истинностных значениях $A,B$ формулы слева и справа от стрелки $\Leftrightarrow$ принимают одинаковые значения $\T$ или $\F$. В принципе, в законах дистрибутивности и правилах де-Моргана также можно использовать $\Leftrightarrow$, тогда они будут не формулами, а правилами вывода (способами получения новых формул). Отметим также специфические для булевой алгебры правила поглощения и всегда ложные и истинные формулы: $$ \left\{ \begin{array}{lcl} A\,\&\,A &\leftrightarrow& A\\ A\vee A &\leftrightarrow& A \end{array} \right. ~~~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} A\,\&\,(A\vee B) &\leftrightarrow& A \\ A\vee (A\,\&\,B) &\leftrightarrow& A \end{array} \right. ~~~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} A\,\&\,\neg A &\equiv& \F \\ A\vee \neg A &\equiv& \T \end{array} \right. $$ Все эти примеры тождеств булевой алгебры являются тавтологиями (всегда истинными формулами), что проверяются при помощи таблиц истинности (перебераются все значения $\F,~\T$ входящих в них высказываний).

Импликация $A\to B$ в формулах часто используется для выражения словесных конструкций типа "если $A$, то $B$".
Хотя импликация истинна и для утверждений "Если Париж столица Англии, то Земля плоская" ($\F \to \F$ истинно), но обычно существует некоторая причинная связь между посылкой $A$ и следствием $B$. Важно помнить, что утверждаемое в импликации предполагает истинность посылки. Что будет при её ложности - умалчивается. Фраза "Если Машу не трогать, то она будет счастлива", ничего не сообщает о том, что произойдёт, если Машу потрогать.
Аналогично, в арифметике при любом $x$, истинна формула $(x\lt 2) \to (x\lt 4)$. Когда посылка истинна ($x=1$), истинно и следствие. Если посылка ложна, то следствие может быть как истинным ($x=3$), так и ложным ($x=5$).

Кванторы

Важную роль при построении формул формальной теории играют кванторы:

Для конечных множеств $x\in\{a_1,\,...,\,a_n\}$ кванторы эквивалентны цепочке дизъюнкций и конъюнкций: $$ \exists_x \,P(x)~~~\Leftrightarrow~~~P(a_1)\vee P(a_2)\vee .... \vee P(a_n),~~~~~~~~~~~~~~~ \forall_x \,P(x)~~~\Leftrightarrow~~~P(a_1)\,\&\, P(a_2)\,\&\, .... \,\&\, P(a_n). $$ Действительно, "существует" означает, что или $P(a_1)$ истинно, или $P(a_2)$ истинно, или,...(хотя бы один из них). Аналогично должны быть истинными все $P(a_i)$ для квантора общности.

Для конечных множеств $\exists_x \,P(x)$ и $\forall_x \,P(x)$ можно вычислить, зная истинность предиката $P(x)$ для каждого $x$. Для бесконечных множеств это уже не так. Точнее, если множество счётно и объект со свойством $P(x)$, существует, то рано или поздно он встретися в цепочке $P(a_1)\vee P(a_2)\vee...$ Если же такого объекта нет, "переборный алгоритм" никогда не остановится. Аналогично, если формула $\forall_x\, P(x)$ истинна, то перебором этого проверить нельзя, хотя можно установить её ложность, получив $P(a_i)\equiv 0$.

Кванторы аналогичны знаку суммирования и их "индекс" может быть обозначен любой переменной.
Формула, в которой все переменные связаны кванторами, называется замкнутой (не содержащей свободных переменных). Например, пусть кванторы в выражениях имеют самый высокий приоритет (действуют первыми). Тогда формула $\forall_x\,P(x,y)~\to~\exists_y\,Q(x,y)$ - это предикат $F(x,y)$ с двумя аргументами: $ \bigr(\forall_u\,P(u,y)\bigr)~\to~\bigr(\exists_v\,Q(x,v)\bigr). $
Свободные переменные (выше $x,y$) называют параметрами формулы, а связанные ($u,v$) - просто переменными.

Однотипные кванторы можно переставлять местами (и также для квантора существования $\exists$): $$ \forall_x\,\forall_y \,P(x,y) ~~~~~\Leftrightarrow~~~~~ \forall_y\,\forall_x\, P(x,y)~~~~~\Leftrightarrow~~~~~ \forall_{x,y}\, P(x,y). $$ Разнотипные кванторы в общем случае переставлять нельзя. Так, $\forall_y\, \exists_x \,\text{Mather}(x,y)$ означает, что у каждого $y$ есть мать $x$, а $\exists_x\,\forall_y \, \text{Mather}(x,y)$ означает, что существует такая $x$, которая является матерью всех, включая себя саму.

Для кванторов, при помощи булевой алгебры, несложно получать различные тождества. Например, из правил де-Моргана следует, что не существует такого $x$, что $P(x)$ истинно, эквивалентно, что для всех $P(x)$ ложно: $$ \neg\exists_x\,P(x)~~~\Leftrightarrow~~~\forall_x\,\neg P(x), ~~~~~~~~~~~~~~~~~~~ \neg\forall_x\,P(x)~~~\Leftrightarrow~~~\exists_x\,\neg P(x). $$ Для любого квантора ($\text{K}_x$ это $\forall_x$ или $\exists_x$) выполняются правила расширения действия, а для "родственных" операций ($\&$ для $\forall$ и $\vee$ для $\exists$) - правила объединения: $$ \left\{ \begin{array}{lcl} \text{K}_x\, P(x)\,\&\, Q~~~&\Leftrightarrow&~~~ \text{K}_x\, \bigr(P(x)\,\&\, Q\bigr)\\ \text{K}_x\, P(x)\vee Q~~~&\Leftrightarrow&~~~ \text{K}_x\, \bigr(P(x)\vee Q\bigr)\\ \end{array} \right. ~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} \forall_{x}\,P(x)~\,\&~\forall_{y}\,Q(y)~~~&\Leftrightarrow&~~~\forall_{x}\,\bigr(P(x)\,\&\,Q(x)\bigr) \\ \exists_{x}\,P(x)\,\vee\,\exists_{y}\,Q(y)~~~&\Leftrightarrow&~~~ \exists_{x}\,\bigr(P(x)\vee Q(x)\bigr) \end{array} \right. $$ В правилах расширения важно, что формула $Q$ не зависит от переменной $x$ (но может зависеть от параметров). Благодаря этому, $Q$ равно либо $\T$, либо $\F$. Перебирая эти два варианта легко проверить истинность этих правил.

◊ Пусть $x\in \mathbb{Z}=\{0,\pm 1,\pm 2,...\}$ (целые числа), функция сложения $x+y$ и предикат равенства $x=y$ определены обычным образом. Для ниже идущих формул первые две истинны, а вторые две - ложны: $$ (a)~~~\exists_{x,y}\,[x+y=5],~~~~~~~~~~(b)~~~\forall_x\,\exists_y\,[x+y = 5],~~~~~~~~(c)~~~\forall_{x,y}\,[x+y = 5],~~~~~~~(d)~~~\exists_y\,\forall_x\,[x+y = 5]. $$ Для $(a)$ существуют, например $x=2$, $y=3$. В $(b)$, для любого $x$ существует $y=5-x$.

◊ Для натуральных чисел $x\in\mathbb{N}=\{0,1,2,...\}$ выразим (определим) отношение $x\mid y:$ "число $x$ делится на $y$" через функцию умножения $x\cdot y$ и запишем следующие утверждения: "Некоторые чётные числа делятся на $4$"; "Каждое число, делящееся на $4$, делится и на $2$": $$ (x\mid y) ~~~\Leftrightarrow~~~\exists_z\,(x=y\cdot z)~~\&~~y\neq 0,~~~~~~~~~~~~ \exists_x\,\bigr[\, (x\mid 2)~\&~(x\mid 4)\,\bigr],~~~~~~~~~~~~ \forall_x\,\bigr[\,(x\mid 4) ~\to~(x\mid 2)\,\bigr]. $$

Предварённой формой формулы называется её эквивалентная запись в которой действие всех кванторов охватывает формулу. Например, $$ \forall_x\, P(x)\,\&\,\exists_y\,Q(y)~\to~\exists_z\,R(z)~~~~~\Leftrightarrow~~~~~~ \exists_x\, \bar{P}(x)~\vee~ \forall_y\,\bar{Q}(y)~\vee~\exists_z\,R(z) ~~~~~\Leftrightarrow~~~~~~\exists_x\,\forall_y\,\bigr[ P(x)\,\&\,\,Q(y)~\to~R(x)\bigr], $$ где после устранения импликации, применено правило объединения для $\exists_x,\,\exists_y$, а затем правила расширения.

Интерпретации теории

Интерпретация формальной теории - это придание элементам сигнатуры содержательного смысла (семантики).
Для этого задаются конкретные непустые множества (из конечного или бесконечного числа элементов). На этих множествах определяются константы, действия функций и значения ($\F ,\T $) предикатов.

Если в сигнатуре есть только высказывания, то общезначимая формула называется тавтологией ($A\vee \neg A$).
Если подформулы произвольной формулы можно обозначить как высказывания таким образом, чтобы получилась тавтология, то эта формула общезначима. Например, $\forall_x\,P(x) \,\vee\, \neg \forall_y\,P(y)$ - это тавтология. В тоже время общезначимая формула $\forall_x P(x)\,\to \exists_y\,P(y)$ тавтологией не является.

Модель формулы - это интерпретация в которой эта формула истинна. Если модель есть, то формула выполнимая.
Модель теории - это интерпретация в которой истинны все аксиомы и теоремы теории.

◊ Рассмотрим предметную теорию с двумя предикатами: $x=y$ (равенство), $x \prec y$ (порядок) и одной функцией: $x\circ y$ (что бы она не обозначала). Возьмём множество из трёх элементов, которые пронумеруем числами: $\mathbb{X}=\{0,1,2\}$. На этом множестве определим две различные интерпретации:

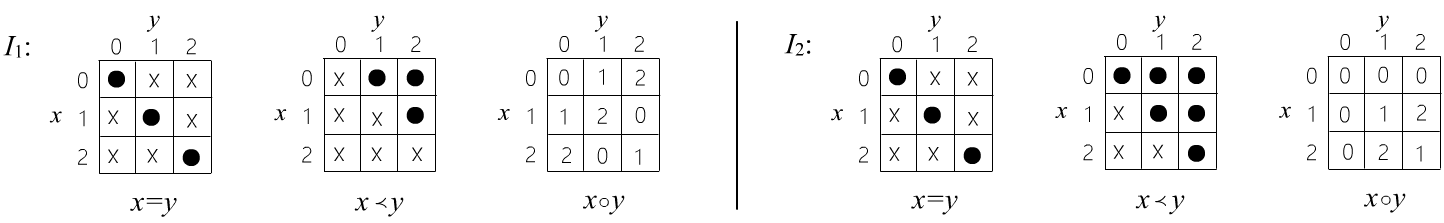
В таблицах для предикатов точка обозначает истину, а крестик - ложь. Например $2=2$ истинно, $2=1$ - ложно. Предикат $x=y$ в обоих интерпретациях определён одинаково, а остальные объекты сигнатуры имеют различные значения. Легко проверить, что в обоих сигнатурах истинна формула $\forall_{x,y}\,[ (x\circ y) = (y\circ x) ]$ (коммутативность). Формула $\forall_x\,\exists_y\, (x\prec y)$ в ложна первой интерпретации и истинна во второй, а $\exists_x\,\forall_y\,(x\prec y)~\to~\forall_y\,\exists_x\,(x\prec y)$ истинна в обоих интерпретациях (на самом деле это общезначимая формула).

Логическое следование

Представим себе множество интерпретаций $\mathcal{I}$, элементами которого являются предметные множества с заданными на них интерпретациями. Два одинаковых множества, на которых по-разному определены функции и предикаты - это различные элементы множества $\mathcal{I}$. Будем считать, что любая замкнутая формула (без параметров) в данной интерпретации либо истинна, либо ложна (для конечных множеств это очевидно). Тогда на множестве интерпретаций $\mathcal{I}$ существуют подмножества истинности каждой формулы (множество её моделей).

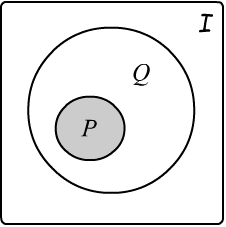
Из формулы $P$ логически следует формула $Q$, если всегда, когда истинна $P$, будет также истинна и $Q$. На множестве интерпретаций область истинности $P$ - это подмножество истинности $Q$. Следствие принято обозначать так: $P\vDash Q$, а если $Q$ общезначима, то: $\vDash Q$.

Логический вывод $\mathcal{P}\Rightarrow Q$ - это получение из формул $\mathcal{P}$ новой формулы $Q$, так что $\mathcal{P}\vDash Q$. Например, в modus ponens: $P,~P\to Q~ \Rightarrow~ Q$ (MP), из формул $P$ и $P\to Q$ выводима $Q$. При этом $Q$ истинна по меньшей мере на тех же интерпретациях, где истинны $P$ и $P\to Q$.

Определения логического вывода и импликации приводят к такому полезному утверждению:

если $~~P\Rightarrow Q,~~$ то $~~~\vDash~P\to Q~~$ (формула является общезначимой) и наоборот по (MP).
Например, вывод по modus ponens эквивалентен общезначимой формуле $(P\,\&\,(P\to Q)) \to Q$, которая, в свою очередь, эквивалентна $(P\,\&\,Q)\,\to\,Q$.

Ещё одна общезначимая формула $P\to (P\vee Q)$ соответствует логическому выводу $P~\Rightarrow~ P\vee Q$ (если истинно $P$, то независимо от значения формулы $Q$ будет истинным и $P\vee Q$).

Справа на рисунке приведена некоторая теория с двумя аксиомами $A_1,A_2$. Их области истинности ограничены жирными линиями. Из аксиом следуют три формулы (= теоремы) $T_1, T_2, T_3$. Это так, потому, что пересечение областей истинности аксиом $A_1$, $A_2$ (закрашенная область) является подмножеством областей истинности всех трёх теорем. Кроме этого, существует вывод $T_1\Rightarrow T_2$, однако из $T_1$ или $T_2$ не следует (и не может быть выведена) $T_3$. Для вывода теорем $T_1$, $T_2$, необходимы обе аксиомы $A_1$ и $A_2$. Для вывода $T_3$ достаточно только аксиомы $A_2$. Формула $T_4$ всегда ложна в данной теории (логически следует и выводимо её отрицание $\neg T_4$).

✒ Приведём примеры односторонних правил логического вывода для формул с кванторами: $$ \forall_x\,P(x)~~~\Rightarrow~~~ P(x)~~~\Rightarrow~~~ P(t)~~~\Rightarrow~~~ \exists_x\,P(x). $$ Первое правило опускания квантора общности $\forall_x\,P(x)~\Rightarrow~ P(x)$ означает, что если утверждение $P(x)$ истинно при любом $x$, то формула $P(x)$ будет общезначима (всегда истинна), какое бы значение $x$ в неё не подставили. Обратное следование, вообще говоря, не верно. В частности $P(x)\,\to\,\forall_y\,P(y)$ не общезначима, например для $x\in\{a_1,a_2\}$ для $P(a_1)\equiv\T$, $P(a_2)\equiv\F$ при $x=a_1$. А вот $\forall_y\,P(y)~\to~ P(x)$ - это общезначимая формула.

Следующее следование $P(x)~~\Rightarrow~~ P(t)$ означает возможность подстановки на место переменной $x$ в уже выведенной формуле $P(x)$ вместо параметра $x$ любого терма $t$ (константы, другой переменной или функции). Так, из формулы $x+y=y+x$ выводится $x+(x+1)=(x+1)+x$ при одновременной замене $y$ на $x+1$.

Последнее одностороннее следование $P(t)~\Rightarrow~\exists_x\,P(x)$ означает что, если $P(t)$ истинно при данном значении терма $t$, то это значение (хотя бы одно) и существует. В обратную сторону такое следствие, в общем случае, также неверно и формула $\exists_y\,P(y)~\to~P(x)$ не общезначима (невыполнима на $P(a_1)\equiv \T$, $P(a_2)\equiv \F$ при $x=a_2$).

Если формула $Q(x)$ выведена непосредственно из аксиом (без использования посылок) после опускания квантора общности $\forall_x\,P(x)~\Rightarrow~ P(x)~\Rightarrow~...~\Rightarrow~Q(x)$, то она справедлива для любого $x$ и можно применить правило обобщения $Q(x)~\Rightarrow~\forall_x\,Q(x)$.

☯ К сожалению, понятие истинности формулы на данной интерпретации хорошо определено только для конечных множеств. Для бесконечных множеств "вычислить" её истинность не всегда возможно. При этом, есть формулы, истинные на всех конечных множествах и ложные на бесконечных. Например, на конечных, линейно упорядоченных множествах с отношением $x\preceq y$ всегда есть наибольшие элементы: $\exists_y\forall_x (x\preceq y)$. Для бесконечных множеств, например, натуральных чисел - это уже не так.

Тем не менее, концепция существования подмножеств истинности формул на множестве интерпретаций важна для понимания аксиоматических свойств формальных теорий и иногда оказывается полезной на практике. Например, вместо построения вывода формулы из аксиом, интеллектуальная система может увериться в её "эмпирической истинности", проделав проверку логического следования на большом числе интерпретаций.

Доказательство от противного

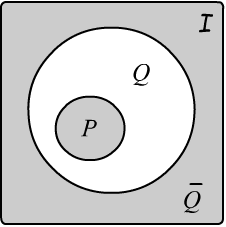Рисунок справа иллюстрирует очень мощный способ доказательства от противного.
Вместо вывода $P \Rightarrow Q$, берётся отрицание $Q$ ("пусть $Q$ неверно..."). Если в результате логических выводов из этих формул получается противоречие $P,\,\neg{Q}~\Rightarrow~\F$ , то тогда $P \Rightarrow Q$. Действительно, если $P \Rightarrow Q$, то область истинности $P$ является подмножеством $Q$ и не имеет общей модели с областью истинности $\neg Q$. Поэтому множество формул $\{P,\,\neg{Q}\}$ или формула $P\,\&\,\neg{Q}$ невыполнима, т.е. противоречива.

Для многих утверждений прямое доказательство либо не известно, либо длиннее доказательства от противного (особенно при размышлениях о существовании или несуществовании объектов с некоторыми свойствами).

◊ Классический пример - это доказательство того, что $\sqrt{2}$ не представимо в виде $n/m$, где $n,m\in \mathbb{N}^+=\{1,2,...\}$.
В качестве $P$ выступают аксиомы арифметики. Докажем формулу $Q:~\sqrt{2}\neq n/m$, где $n/m$ несократимая дробь.
Пусть $\bar{Q}: ~\sqrt{2}=n/m$. Возводя в квадрат имеем $n^2=2\,m^2$ и следовательно $n$ - чётно, т.е. представимо как $n=2\,k$.
Но тогда $(2k)^2 = 2m^2$ или $m^2 = 2k^2$, т.е. $m$ - также чётно, а это противоречит несократимости дроби $n/m$.

В теории предикатов доказательство от противного позволяет избавляться от кванторов и сводить логический ввод к простой процедуре, которую обычно используют в программах машинного доказательства теорем.

Рассмотрим сначала формулу вида $S:~\exists_x\,P(x)$. Пусть необходимо доказать, что она невыполнима. Добавим в сигнатуру теории новую константу $a$ и запишем формулу $S':~P(a)$. Формулы $S$ и $S'$ не эквивалентны и в частности $\exists_x\,P(x)~\to~P(a)$ необщезначима (её опровергающая интерпретация: $x\in\{a,b\}$, $P(a)\equiv \F$, $P(b)\equiv \T$).
Это и понятно. Формула $\exists_x\,P(x)$ не утверждает, что существующий $x$ единственен, тогда как в $P(a)$ существующая константа введена в единственном экземпляре.

Тем не менее, справедливо следующее утверждение "если $S'$ невыполнима, то невыполнимой будет и формула $S$."
Действительно, пусть $P(a)$ невыполнима, а $\exists_x\,P(x)$ выполнима, т.е. существует модель в которой $\exists_x\,P(x)$ истинно.
Это возможно, только если есть такой $x$, что $P(x)$ истинно, что противоречит невыполнимости формулы $P(a)$.

В общем случае устранение кванторов требует введения не только констант но и новых сколемовских функций. Например, формула $\forall_x\,\exists_y\,P(x,y)$ означает, что для каждого $x$ существует такой $y=f(x)$, что $P(x,f(y))$ истинно. Как и с константами, такой переход не является логическим выводом. Однако, если $P(x,f(y))$ будет невыполнимо, то невыполнимой будет и формула $\forall_x\,\exists_y\,P(x,y)$.

Введение скулемовских констант и функций проводится слева-направо (стрелка $\mapsto$ это не импликация, а переход от формулы $S$ к формуле $S'$): $$ \exists_x\,\forall_{y,z}\,\exists_u\,\forall_v\,\exists_w\,P(x,y,z,u,v,w) ~~~~\mapsto~~~~ \forall_{y,z,v}\,\exists_w\,P(a,y,z,f(x,y),v,w) ~~~~\mapsto~~~~ \forall_{y,z,v}\,P(a,y,z,f(y,z),v,g(y,z,v)), $$ где для константы $a$ и функций $f$, $g$ необходимо использовать символы отличные от тех, что заданы в сигнатуре. При этом в $\exists_{x,y}\,P(x,y)~~\mapsto~~P(a,b)$ константы должны быть различными.

◊ Докажем общезначимость следующей формулы: $\exists_x\,\forall_y\,R(x,y)~\to~\forall_y\,\exists_x\,R(x,y)$ от противного, взяв её отрицание: $\neg(A\to B)~~\Leftrightarrow~~ \neg(\neg A\vee B)~~\Leftrightarrow~~ A\,\&\,\neg B$ и введя сколемовские константы $a,b$: $$ \exists_x\,\forall_y\,R(x,y)~\,\&\,~\exists_y\,\forall_x\,\bar{R}(x,y) ~~~~\Leftrightarrow~~~~~ \exists_x\,\forall_y\,R(x,y),~~~~~\exists_y\,\forall_x\,\bar{R}(x,y) ~~~~~\mapsto~~~~~ \forall_y\,R(a,y),~~~~~\forall_x\bar{R}(x,b). $$ Так как эти две формулы должны быть истинными при любых $x,y$, можно положить $y=b$ и $x=a$, получив противоречие: $R(a,b),~~\bar{R}(a,b)$.

Исчисления и выводимость

Вершиной формализации математики является "Игра в слова". В этой игре фиксируется алфавит символов $\Sigma$ из которых формируются слова. Некоторое подмножество $\mathcal{L}\subseteq \Sigma^{*}$ всех возможных слов $\Sigma^{*}$ называется языком (это "синтаксически правильные" слова). Часть слов языка $\mathcal{A} \subset \mathcal{L}$ объявляется аксиомами. Затем фиксируются правила вывода, которые по некоторому набору слов порождают новое слово из $\mathcal{L}$. Если из данного множества слов $\mathcal{P}\subset \mathcal{L}$ и аксиом $\mathcal{A}$, при помощи правил вывода, порождается цепочка слов, которая оканчивается словом $Q$, то говорят, что оно выводимо из множества слов: $\mathcal{P} \vdash Q$. Если для вывода $Q$ необходимы только аксиомы, то говорят, что $Q$ просто выводимо: $\vdash Q$. Тройка {язык, аксиомы, правила вывода} называется исчислением.
Вывод $\vdash Q$ в исчислении является чисто синтаксической процедурой, не использующей семантики теории типа истинности или ложности формул (в отличии от семантики логического вывода $\mathcal{P}\Rightarrow Q$).

◊ Пусть словарь состоит из двух символов $\Sigma=\{a,b\}$, а множество аксиом из четырёх слов $\mathcal{A}=\{a,~b,~aa,~bb\}$ и есть два правила вывода: $W~\vdash~ aWa$ и $W~\vdash~ bWb$, где $W$ - любое выведенное ранее слово. Это исчисление порождает все двухбуквенные палиндромы типа $aba$, $abbba$, $bbaaabbaaabb$ и т.д.

Разрешимой называется теория, для которой существует алгоритм, позволяющий выяснить - выводима данная формула из аксиом или нет. Если такого алгоритма нет, теория называется неразрешимой. Теория с палиндромами из примера выше, очевидно, разрешима.

В некоторых теориях можно перечислить все её теоремы. Такие теории называются полуразрешимыми. В них за конечное число шагов можно подтвердить, что теорема выводима (найти её в списке перечисления), но алгоритм никогда не остановиться для невыводимых формул. К сожалению, многие содержательные теории неразрешимы.

Важную роль играет исчисление предикатов и его частный случай - исчисление высказываний. В качестве слов в исчислении предикатов выступают формулы, состоящие из символов $\Sigma=\{\neg~\,\&~\vee~\to~\leftrightarrow~\forall\,~\exists\,~A~f~x~c~(~~)~,\}$. Произвольные предметные переменные $x$, $xx$, $xxx$ для краткости обозначаются как $x,~y,~z$ и аналогично для предикатных $A$, функциональных $f$ и константных символов $c$. Язык (синтаксически верные формулы) определяется по индукции: "если $P$ и $Q$ формулы, то $(P\vee Q)$ тоже формула", и т.д.

В отличии от предметных теорий с заданной сигнатурой, аксиомы исчисления предикатов являются "очевидно" общезначимыми формулами (истинными на всех интерпретациях). Правила вывода выбирают так, чтобы общезначимость сохранялась. Поэтому общезначимыми являются и все выводимые теоремы исчисления. Например формула $\exists_x\,\forall_y\,A(x,y)~\to~\forall_y\,\exists_x\,A(x,y)$ - это теорема исчисления, а $\forall_y\,\exists_x\,A(x,y)~\to~\exists_x\,\forall_y\,A(x,y)$ - уже нет (она не общезначима). Роль $A$ может играть любой предикат или формула конкретной предметной теории. Теоремы исчисления предикатов являются подмножеством теорем любой предметной теории. Области истинности теорем исчисления - это всё пространство интерпретаций (в отличии от осмысленных теорем предметной теории). Так, $\forall_{x,y}[(x\lt y)\,\to\,\neg(y\lt x)]$ это теорема в предметной теории (например, в арифметике), а $\forall_{x,y}[(x\lt y)\,\vee\,\neg(x\lt y)]$ это общезначимая теорема исчисления.

В принципе, в исчислении предикатов символы выводимости $\vdash$ и $\Rightarrow$ равносильны. Когда пишут более общий символ $\vdash$, принятый в произвольных исчислениях, подчёркивают, что при выводе истинность формул роли не играет, а просто идёт "игра в слова". Но в любом случае, все выводимые в исчислении предикатов формулы общезначимы. Справедливо также обратное утверждение Гёделя о полноте:

если формула $P$ общезначима: $\vDash~P$, то она выводима: $\vdash~P$.
В исчислении высказываний утверждение достаточно очевидное. Его теоремы являются тождествами булевой алгебры. Приведение любой формулы при помощи этой алгебры в конъюнктивную нормальную форму: $(P_1\vee P_2\vee...)\,\&\,(Q_1\vee Q_2\vee...)\,\&\,...$ позволяет доказать её истинность.

◊ Докажем, что $P\to(\bar{P}\to Q)$ общезначима. Переходя от импликации к дизъюнкции, имеем: $$ P\to(\bar{P}\to Q)~~~\Leftrightarrow~~~\bar{P}\vee (P\vee Q)~~~\Leftrightarrow~~~(\bar{P}\vee P)\vee Q~~~\Leftrightarrow~~~\T\vee Q ~~~\Leftrightarrow~~~\T. $$ Двигаясь в обратную сторону, из "аксиом" $\bar{P}\vee P$, $~~~\T\vee P$, правил $P~\Rightarrow~P\vee Q$, $P\vee Q~\Rightarrow~Q\vee P$ и т.п. можно вывести исходную формулу.

Всегда представляет интерес формулировка независимых аксиом и правил вывода. Для исчисления предикатов, например, можно выбрать следующие слова: $$ \begin{array}{lcl} P~\to~(Q\to P),\\ (P~\to~(Q\to R))~\to~((P\to Q)\to(P\to R)),\\ (\neg Q\to \neg P) ~\to~((\neg Q\to P)\to Q), \end{array} ~~~~~~~~~~~~~~~~~~~ \begin{array}{lcl} \forall_x\,A(x)~\to~A(t),\\ \forall_x\,(P\to Q(x))~\to~(P\to\forall_x\,Q(x))\\ ~\\ \end{array}, $$ где $P,Q,R$ - любые уже полученные ранее слова и в последней аксиоме в $P$ нет $x$. Такой бесконечный набор аксиом называется схемой аксиом. В качестве правил вывода достаточно взять правило modus pones и правило обобщения: $$ P,~~P\to Q~~~~~\vdash~~~~~Q,~~~~~~~~~~~~~~~~~~~~~~P(x)~~~\vdash~~~\forall_x\,P(x). $$ Эти аксиомы и правила позволяют вывести все строки, которые в семантической трактовке являются общезначимыми формулами исчисления предикатов.

Непротиворечивость и независимость аксиом

Назовём теорией любое конечное или бесконечное множество $\mathcal{T}$ замкнутых, синаксически правильных формул.
Вывод в теории $\mathcal{T}$ формулы $Q$ (из формул $\mathcal{T}$ и любых общезначимых формул) обозначим как $\mathcal{T}\vdash Q$.
В общем случае $Q$ не общезначима: $\not\vDash Q$, но, логически следует из теории $\mathcal{T}\vDash Q$ (пересечение областей истинности формул $\mathcal{T}$ является подмножеством области истинности $Q$). Часть формул $\mathcal{A}\subseteq \mathcal{T}$ можно назвать аксиомами. Аксиомы любой, уважающей себя предметной теории, должны быть непротиворечивыми, независимыми и, по-возможности, полными.

✒ Теория непротиворечива, если её аксиомы $A_1$, $A_2,...$ на множестве интерпретаций $\mathcal{I}$ пересекаются, т.е. (существует хотя бы одна интерпретация $=$ модель на которой аксиомы одновременно истинны (справа точка $M$). В непротиворечивой теории $\mathcal{T}$, при помощи вывода, нельзя получить некоторое утверждение $P$ и его отрицание $\bar{P}$. Действительно, если из аксиом логически следует $P$, то область пересечения аксиом (если она есть!) является его подмножеством и не может быть подмножеством $\bar{P}$, и наоборот (см. рисунок).

В противоречивой теории $\mathcal{T}$ существует такое $P$, что $\mathcal{T} \vdash P$ и $\mathcal{T} \vdash \bar{P}$. В подобной теории можно вывести любое утверждение, поэтому пользы от неё немного. Действительно, из $P,\,\bar{P}$ и тавтологии $P\to(\bar{P}\to Q)$ дважды по правилу modus ponens следует $Q$ (произвольная формула).

✒ Независимость означает, что никакая аксиома не может быть выведена из других аксиом.
В частности, множества истинности таких аксиом не включают полностью в себя другие аксиомы. Чтобы доказать независимость аксиомы $A_1$ от аксиом $A_2,A_3,...$, необходимо построить такую интерпретацию, в которой все $A_2,A_3,...$ истинны, а $A_1$ - ложна. Это и означает, что область истинности $A_1$ не является подмножеством пересечения областей истинности аксиом $A_2,A_3,...$.

Если данная теория непротиворечива, а её аксиомы $A_1,...,A_n$ независимы, то новая теория, в которой одна из аксиом заменена на её отрицание, также является непротиворечивой. Справа закрашена область истинности пересечения аксиом $A_2,...,A_n$. Граница истинности аксиомы $A_1$ делит её на две части. В первой части $(1)$ находятся модели исходной теории, а во второй $(2)$ - модели новой теории, в которой $A_1\mapsto \bar{A}_1$.

Чем "больше" моделей в теории, тем "слабее", обычно, система аксиом. Действительно, при "большой" области пересечения аксиом потенциально существует меньше формул (теорем), для которых эта область является подмножеством и которые в этой теории можно вывести.

Полнота теории

Предметная теория $\mathcal{T}$ полна, если она:

1) непротиворечива
2) любая замкнутая формула $P$ либо выводима: $\mathcal{T}\vdash P$, либо выводимо её отрицание: $\mathcal{T}\vdash \bar{P}$.
Полнота достаточно нетривиальное свойство формальной теории и скорее необходимо удивляться существованию полных теорий, чем неполных.

На рисунке приведен пример неполной теории, в которой формулы $P$ и $Q$ пересекают закрашенную область пересечения истинности аксиом (множество моделей теории). Эти формулы логически не следуют из аксиом, и поэтому не могут быть ни выведены, ни опровергнуты. Если их добавить к аксиомам, то получится теория с меньшим числом моделей (тёмно-серый цвет). Однако, если есть бесконечное множество подобных формул, то и их добавление к аксиомам может не приводить к полной теории (непополняемая неполнота).

Конкретная неформальная предметная теория обычно работает с определённым множеством, на котором фиксированы функции и предикаты сигнатуры (модель теории). Например, в арифметике это бесконечное множество натуральных чисел $\mathbb{N}=\{\,0,\,1,\,2,\,...\,\}$. На нём "обычным образом" определён предикат равенства $x=y$ и функции сложения $x+y$ и умножения $x\cdot y$. Все они образуют интерпретацию $I_{\mathbb{N}}$, которая на рисунке выше обозначена жирной точкой (находится в области истинности аксиом арифметики). Вполне естественно допустить существование таких формул, которые истинны на $I_{\mathbb{N}}$, но при этом невыводимы (выше формула $P$).
В этом состоит содержание теоремы Гёделя о неполноте арифметики c аксиомами Пеано (PA).

◈ Замечательным следствием теоремы о полноте исчисления предикатов (если $\vDash P$, то $\vdash P$) является эквивалентность логического следствия и выводимости в любой теории $\mathcal{T}$:

Если $~~~\mathcal{T}\vDash~P,~~~$ то $~~~\mathcal{T} \vdash~P~~~$ и наоборот.
Действительно, пусть пересечение областей истинности формул $\mathcal{T}$ это подмножество области истинности $P$.
Тогда по определению импликации формула $\mathcal{T} \to P$ является тавтологией: $\mathcal{T}\vDash Q~~\Rightarrow~~\vDash \mathcal{T}\to Q~~$ (под $\mathcal{T}$ в формуле можно понимать конъюнкцию всех формул $\mathcal{T}$). А раз так, то по теореме о полноте исчисления она выводима из общелогических аксиом (тавтологий): $\vdash \mathcal{T} \to P$. Соответственно, по правилу modus ponens получаем $\mathcal{T},~\mathcal{T} \to P ~\vdash~ P$ или (опуская, как обычно, общезначимую формулу) $\mathcal{T}\vdash P$. В обратную сторону следствие очевидно по построению правил вывода, которые сохраняют свойство логического следствия.

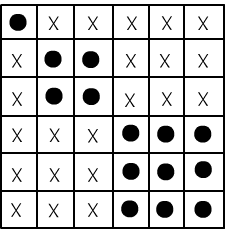◊ Простым примером неполной теории является теория эквивалентности, сигнатура которой содержит отношение $x\sim y$, удовлетворяющее аксиомами рефлексивности, симметричности и транзитивности: $$ \forall_x\,(x\sim x),~~~~~~~~~~~~~\forall_{x,y}\,\bigr[(x\sim y)~\to~(y\sim x)\bigr],~~~~~~~~~~~~\forall_{x,y,z}\,\bigr[(x\sim y)\,\&\,(y\sim z)~\to~(x\sim z)\bigr]. $$ В этой теории невыводима формула $T:~\forall_{x,y}\,(x\sim y)$ так как она ложна на любом множестве из двух и более элементов, где $x\sim y$ это "обычное" равенство (аксиомы на этих интерпретациях выполнимы). В тоже время её отрицание $\bar{T}:~\exists_{x,y}\,\neg(x\sim y)$ ложна на одноэлементном множестве $\mathbb{M}=\{a \}$ с $(a\sim a)\equiv \T$ (все аксиомы при этом также выполняются).

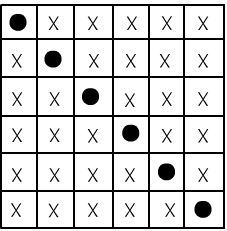
Отношение равенства $x=y$ удовлетворяет тем же аксиомам, что и отношение эквивалентности $x\sim y$. Кроме этого добавляются бесконечный набор формул (схемы аксиом) утверждающие, что если совпадают аргументы у функций или предикатов сигнатур, то должны совпадать и их значения. Например, если в сигнатуре есть функция $f(x,y)$ и предикат $P(x)$, то добавляются аксиомы: $$ \forall_{x_1,y_1,x_2,y_2}\,\bigr[(x_1=x_2)\,\&\,(y_1=y_2)~\to~f(x_1,y_1)=f(x_2,y_2)\bigr], ~~~~~~~ \forall_{x_1,x_2}\,\bigr[(x_1=x_2)~~\to~~ (P(x_1) \leftrightarrow P(x_2))\bigr]. $$ Теория, в сигнатуре которой присутствует отношение равенства называется нормальной. В таких теориях аксиомы равенства не повторяют, но подразумевают их наличие.

◊ Простейший пример полной теории состоит из "пустой" сигнатуры, в которой есть только равенство $x=y$, аксиомы которого дополнены формулой $\forall_{x,y}\,(x=y)$. Единственной моделью этой теории является одноэлементное множество $\{a\}$ с $a=a$ равным $\T$. Любая формула эту модель либо включает (формула выводима), либо нет (формула невыводима).

Аксиоматический анализ Алисы и Боба

Вернёмся к теории об Алисе и Бобе и докажем непротиворечивость и независимость её аксиом. В сигнатуре теории есть только утверждения (константные предикаты) $A,B,L$. Для доказательства непротиворечивости достаточно предъявить пример значений высказываний, при которых все аксиомы истинны. В нормальной форме эти аксиомы имеют следующий вид: $$ (\mathbf{A_1}):~~~~\bar{L}\vee \bar{A}\vee \bar{B},~~~~~~~~~~~~~~(\mathbf{A_2}):~~~~~L\vee A,~~~~~~~~~~~~~(\mathbf{A_3}):~~~~~L\vee B. $$ Несложно видеть, что для $A=B=\T $ и $L=\F $ они истинны ($\T \vee Q \equiv \T $).

Чтобы показать независимость аксиом, необходимо построить интерпретацию в которой все аксиомы истинны, кроме одной. В этом простом мире легко описать всё множество интерпретаций в табличной форме. Каждый её элемент - это присваивание логическим высказываниям $A,B,L$ логических значений $\T $ или $\F $:

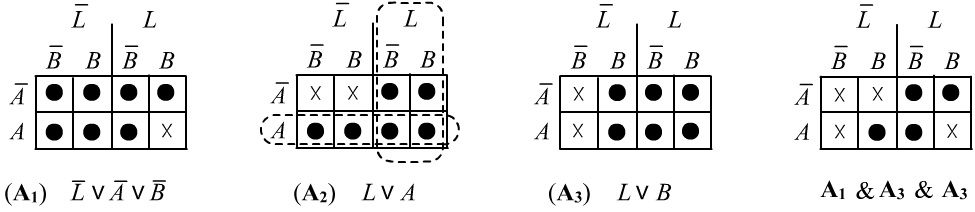
Точки в таблицах помечают истину ($\T $). Их совокупность - это множество истинности формулы. На оставшихся интерпретациях (крестик) - формула ложная ($\F $). Первая аксиома ложна в единственной модели $A=B=L=\T $ (правый нижний угол первой таблицы с крестиком). В этой же модели вторая и третья аксиомы истинны. Поэтому $A_1$ нельзя вывести из $A_2$ и $A_3$. Аналогично несложно найти интерпретации для доказательства независимости $A_2$ от $A_1,A_3$ и $A_3$ от $A_1,A_2$. Так как в нормальной форме высказывания связаны дизъюнкциями, области истинности - это просто объединение областей истинности высказываний (во второй таблице пунктирами выделены истинности $L$ и $A$).

В последней таблице приведена область истинности пересечения всех трёх аксиом конъюнкцией, что соответствует семантике нашей задачи. Заметим, что в истории про Алису и Боба существует очевидная связь $L \leftrightarrow \bar{A}\vee \bar{B}$, выполнение которой и определяет множество истинности задачи. Чтобы вывести эту формулу слева-направо $L\Rightarrow \bar{A}\vee \bar{B}$, необходима первая аксиома, а для вывода в обратном направлении $\bar{A}\vee \bar{B} \Rightarrow L$, необходимы оставшиеся две: $$ L,~\mathbf{A_1}~\Rightarrow~\bar{A}\vee\bar{B},~~~~~~~~~~~~~~~~~~~\bar{A}\vee\bar{B},~\mathbf{A_2},~\mathbf{A_3},~\Rightarrow~L. $$

Рассмотрим как выглядит вывод утверждения $\bar{B}$ из начала документа на языке множества интерпретаций:

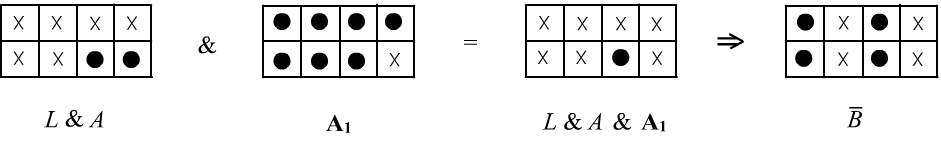
В первой таблице приведено множество истинности исходных посылок $L,A$, вторая таблица - это аксиома $\mathbf{A_1}$ и в третьей - их пересечение при помощи логического И. Эта область истинности (из одной точки) является подмножеством области истинности утверждения $\bar{B}$. Поэтому оно логически следует из посылок и аксиомы $\mathbf{A_1}$, что было продемонстрировано построением соответствующего вывода.

Теория моделей

Напомним, что теория $\mathcal{T}$ - это любое множество замкнутых формул. Теория непротиворечива, если существует интерпретация (модель $M$) в которой все формулы $\mathcal{T}$ истинны. Это обозначается следующим образом: $M\vDash \mathcal{T}$.

Элементарной теорией $\text{Th}(M)$ модели $M$ называется множество всех истинных в $M$ формул. В общем случае теория $\mathcal{T}$ с моделью $M\vDash \mathcal{T}$ может содержать "меньше" формул, чем элементарная теория: $\mathcal{T} \subseteq \text{Th}(M)$.

Все формулы, следующие (и выводимые) из данной теории $\mathcal{T}$ обозначаются как $[\mathcal{T}]$. Например, в качестве $\mathcal{T}$ можно взять аксиомы теории. Тогда множество $[\mathcal{T}]$ содержит как аксиомы, так и все выводимые из них теоремы.

◈ Для любой модели $M$ теория $\text{Th}(M)$ полна.

$\triangleleft$ Действительно, $\text{Th}(M)$ непротиворечива, так как у неё есть модель. Любая формула $P$ в модели $M$ или истинна: $M\vDash P$ или ложна: $M\vDash \neg P$, откуда, либо $P\in \text{Th}(M)$, либо $\neg P\in \text{Th}(M)$. $\square$

◈ Если теория $\mathcal{T}$ полна и $M$ её модель: $M\vDash \mathcal{T}$, то $[\mathcal{T}]=\text{Th}(M)$ и наоборот

$\triangleleft$ От противного. Пусть $P\in \text{Th}(M)$ и $\mathcal{T}\not\vdash P$ (множества $[\mathcal{T}]$ и $\text{Th}(M)$ не совпадают). Тогда, в силу полноты, $\mathcal{T}\vdash \neg P$. Поэтому $M\vDash \neg P$ и $M\not \vDash P$, что противоречит $P\in \text{Th}(M)$. В обратную сторону по предыдущему утверждению. $\square$

Пусть предметы теории принадлежат одному множеству. Интерпретации $M$ и $N$ называют изоморфными: $M\simeq N$, если между всеми элементами $m\in M$ и $n\in N$ есть взаимооднозначное соответствие: $n=\alpha(m)$, $m=\alpha^{-1}(n)$ и для всех констант $c_N=\alpha(c_M)$, всех предикатов $A_M(m_1,m_2,...) \leftrightarrow A_N(\alpha(m_1),\alpha(m_2),...)$ и функций $\alpha\bigr(f_M(m_1,m_2,...)\bigr)=f_N(\alpha(m_1),\alpha(m_2),...)$. Другими словами, в изоморфных интерпретациях все элементы сигнатуры определены одинаково с точностью до переобозначения элементов множеств. Для конечных множеств число элементов в $M$ и $N$ должны быть одинаковыми. Для бесконечных множеств ситуация может быть хитрее:

◊ Пусть есть сигнатура с функцией $f(x,y)$ и константой $c$. Определим две интерпретации. Первая интерпретация $M$ - это множество действительных чисел $\mathbb{R}$, с функцией в виде обычного сложения $f(x,y)=x+y$ и $c=0$. Во второй $N$ - множество неотрицательных действительных чисел $\mathbb{R}^+ \ge 0$ с функцией $f(x,y)=x\cdot y$ и константой $c=1$. Несложно видеть, что $M\simeq N$ с таким соответствием: $n=e^{m}$.

Изоморфизм $M\simeq N$ обладает свойствами эквивалентности (рефлексивно, симметрично и транзитивно), и все изоморфные интерпретации можно считать "одинаковыми".

Модели $M$ и $N$ называются элементарно эквивалентными: $M\leftrightarrow N$, если $\text{Th}(M)=\text{Th}(N)$, т.е. в них истины одни и те же формулы. Изоморфные модели элементарно эквивалентны: $M\simeq N~~\Rightarrow~~M\leftrightarrow N$, но не всегда наоборот.

◈ Если все модели теории $\mathcal{T}$ элементарно эквивалентны, то $\mathcal{T}$ - полная теория и наоборот.

$\triangleleft$ От противного. Пусть $\mathcal{T}$ неполна. Тогда существует формула $P$ для которой $\mathcal{T}\vDash P$ и $\mathcal{T}\vDash \neg P$. Тогда обе теории ${\mathcal{T},~P}$ и ${\mathcal{T},~\neg P}$ выполнимы, т.е. имеют не элементарно эквивалентные модели (теории разные).
Но тогда эти модели будут и моделями $\mathcal{T}$, что противоречит посылке. $\square$