ML: Метрики бинарной классификации

Введение

В этом документе рассмотрены различные метрики, характеризующие работу модели с машинным обучением в задаче бинарной классификации. Модель, получив вектор признаков примера, относит его к одному из двух классов (негативному или позитивному). Названия классов связаны с задачами медицинской диагностики, в которой "хороший" результат теста (нет болезни) называют негативным, а выявленную болезнь - позитивным результатом теста. В подобных задачах часто классы являются несбалансированными. Если следовать медицинской аналогии примеров позитивного класса в этом случае меньше чем негативного (как в обучающих, так и в тестовых данных).

Матрица ошибок

Пусть в обучающих данных есть $\mathrm{neg}$ негативных примеров и $\mathrm{pos}$ - позитивных. Они составляют множество из $N=\mathrm{neg}+\mathrm{pos}$ "истинных" (true) примеров (обучающий дататсет). Число предсказанных (pred) моделью примеров в негативном (neg') и позитивном (pos') классах могут оличаться от истинных. Достаточно полную информацию о работе модели отражает матрицы ошибок (confusion matrix). На её диагонали находятся количества правильных предсказаний:

В остальных двух ячейках матрицы находятся ошибки модели:

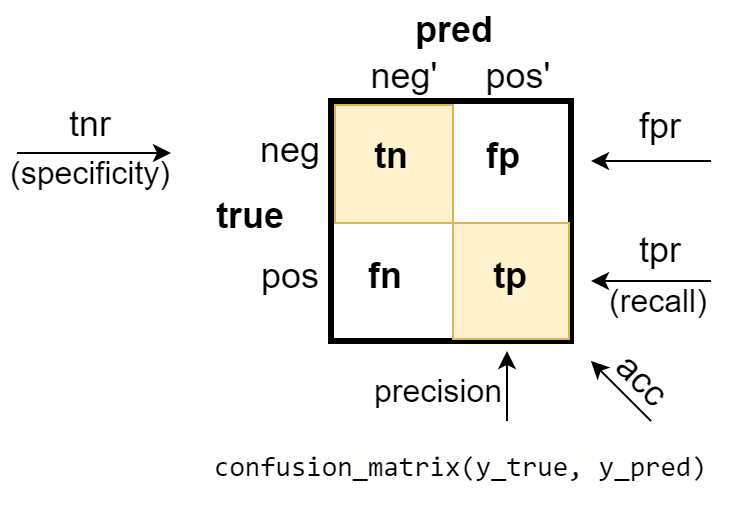
Сумма чисел по строчкам соответствует числу истинных негативных и позитивных примеров, а их отношение npr (negative-positive-rate) говорит о сбалансированности (если npr=1) классов в примерах:

$$ \mathrm{neg}=\mathrm{tn}+\mathrm{fp},~~~~~~~~~~ \mathrm{pos}=\mathrm{fn}+\mathrm{tp},~~~~~~~~~~ \mathrm{npr} = \frac{\mathrm{neg}}{\mathrm{pos}}. $$

Аналогично сумма чисел по колонкам соответствует числу предсказанных негативных и позитивных примеров:

$$ \mathrm{neg}'=\mathrm{tn}+\mathrm{fn},~~~~~~~~~~ \mathrm{pos}'=\mathrm{fp}+\mathrm{tp},~~~~~~~~~~ \mathrm{npr}' = \frac{\mathrm{neg}'}{\mathrm{pos}'}. $$ Понятно что общее число true и pred примеров равны: $N = \mathrm{neg}+\mathrm{pos}=\mathrm{neg}'+\mathrm{pos}'$. Доля негативных и позитивных примеров от их общего числа равны: $$ \frac{\mathrm{neg}}{N} = \frac{\mathrm{npr}}{\mathrm{1+npr}},~~~~~~~~~~~~~~~~~~\frac{\mathrm{pos}}{N} = \frac{1}{\mathrm{1+npr}}. $$ При сильном отличии $\mathrm{npr}$ от единицы, в функции ошибки примеры классов, обычно, взвешиваются с переставленными весами (например, негативные примеры с весом $1$, а позитивные - с весом $\mathrm{npr}$).

Основные метрики

Основными метриками модели являются accuracy (acc) - аккуратность по обоим классам и аккуратности каждого класса в отдельности: true negative rate (tnr) или specificity, или selectivity и true positive rate (tpr) или sensitivity, или recall:

$$ \mathrm{acc} = \frac{\mathrm{tn}+\mathrm{tp}}{\mathrm{neg}+\mathrm{pos}},~~~~~~~~~~~ \mathrm{tnr} = \frac{\mathrm{tn}}{\mathrm{neg}},~~~~~~~~~~~~ \mathrm{tpr} = \frac{\mathrm{tp}}{\mathrm{pos}}. $$

Аккуратность позитивного класса tpr называют также полнотой. В медицинской диагностики позитивный результат теста - это наличие болезни. Поэтому tpr характеризует на сколько полона модель ("нашли все болезни").

В связи с этой аналогией precision или positive predictive value (PPV) (верные предсказания pos-класса к числу всех предсказаний pos-класса) считается точностью (на сколько точно болезнь выявляется): $$ \mathrm{pre} = \frac{\mathrm{tp}}{\mathrm{tp}+\mathrm{fp}} = \frac{\mathrm{tp}}{\mathrm{pos}'}. $$

Иногда позитивный класс, с точки зрения данной предметной области, важнее негативного, а его примеры встречаются существенно реже, чем у негативного. В этом случае больше внимания обращают не на $\mathrm{tfr}$ (как аккуратность негативного класса), а на precision (точность позитивного). В частности баланс между полнотой и точностью характеризует метрика $F_1$, равная геометрическому среднему между этими величинами: $$ \frac{1}{F_1} = \frac{1}{2}\Bigr[\frac{1}{\mathrm{tpr}} + \frac{1}{\mathrm{pre}}\Bigr],~~~~~~~~~~~~~~~F_1 = \frac{2\,\mathrm{tpr}\,\mathrm{pre}}{\mathrm{tpr}+\mathrm{pre}}. $$ Чем ближе $F_1$ к единице (как впрочем и $\mathrm{tpr}$, $\mathrm{pre}$), тем лучше работает модель.

Аккуратность и точность несложно выразить через относительные величины:

$$ \mathrm{acc} = \frac{\mathrm{tpr} + \mathrm{tnr}\cdot \mathrm{npr}}{1 + \mathrm{npr}},~~~~~~~~~~~~~~~~~~~ \mathrm{pre} =\frac{\mathrm{tpr}} {\mathrm{tpr}+\mathrm{npr}\cdot(1-\mathrm{tnr})}. $$ Если классы сбалансированы (npr=1), то общая аккуратность равна среднему значению аккуратности каждого класса: acc=(tnr+tpr)/2 и независимо от npr, если tnr=tpr, то tnr=tpr=acc.

При заметном перекосе классов, можно получить хорошую аккуратность, но модель будет бесполезной (в скобках после аккуратности стоят tnr, tpr): 

                     acc  (tnr,   tpr)   pre   npr  npr'
       80 |  0
cm =  --------       0.90 (1.00, 0.50)  1.00    4    9
       10 | 10
       
       70 | 10
cm =  --------       0.80 (0.86, 0.50)  0.50    4    4
       10 | 10       

       60 | 20
cm =  --------       0.75 (0.75, 0.75)  0.43    4    1.9
        5 | 15

ROC - кривая tpr(fpr)

Обычно модель выдаёт не номера классов, а их вероятности или степень уверенности. В бинарной задачи с двумя классами можно считать, что это одно число, равное $p=0$ для в точности негативного класса и $p=1$ - в точности позитивного. Так как $p$ меняется в интервале $[0...1]$, для определения номера класса, необходимо выбрать пороговое значение вероятности $p_0$. При $p \ge p_0$ пример будет отнесен к позитивному классу, а при $p \lt p_0$ - к негативному. По умолчанию выбирается значение $p_0=0.5$, однако это не единственная и не всегда оптимальная возможность.

Для каждого значения $p_0$ получается своя матрица ошибок и вычисленные на её основе аккуратности классов $\mathrm{tnr},~\mathrm{tpr}$. Вместо $\mathrm{tnr}$ принято использовать дополнительную к нему величину $\mathrm{fpr}=1-\mathrm{tnr}$. Отложим для каждого $p_0$ по горизонтальной оси $\mathrm{fpr}$, а по вертикальной $\mathrm{tnr}$. Полученная линия называется receiver operating characteristic или ROC-кривая:

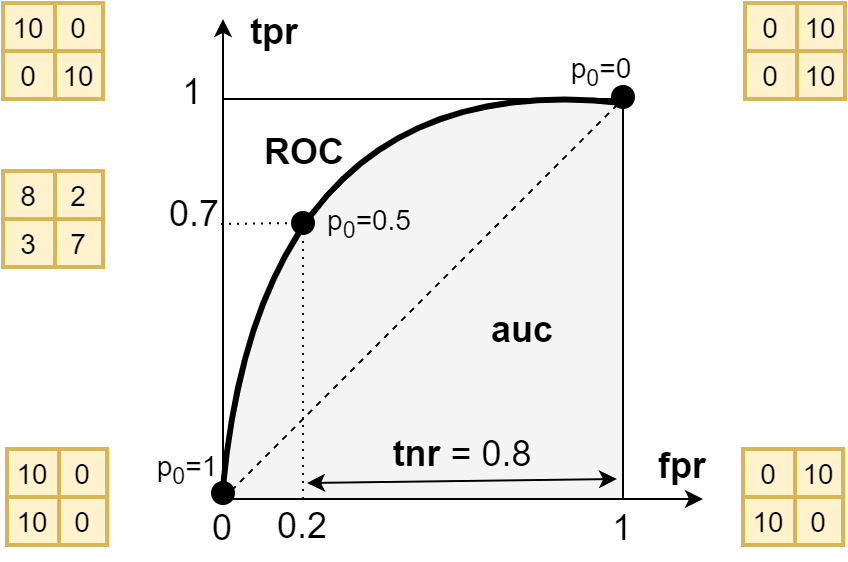
Если $p_0=0$ (верхний, правый угол), то все примеры будут относится к позитивному классу ($\mathrm{fpr}=\mathrm{tpr}=1$), а если $p_0=1$ (нижний, левый угол) - к негативному ($\mathrm{fpr}=\mathrm{tpr}=0$). Хорошая модель должна стремится к левому верхнему углу, (см. его матрицу ошибок). В примере на рисунке, при пороговом значении вероятности $p_0=0.5$ аккуратности негативного и позитивного классов равны $\mathrm{tnr}=0.8$, $\mathrm{tpr}=0.7$ (соответствующая матрица ошибок приведена слева). Уменьшением порога можно увеличить $\mathrm{tpr}$ за счёт снижения $\mathrm{tnr}$.

Метрика auc

Площадь под кривой называется auc-метрикой (Area Under Receiver Operating Characteristic). Чем ближе auc к единице, тем лучше модель.

Пусть $n_{0}(p) = N_0(p)/\mathrm{neg}$ - доля примеров от всех $\mathrm{neg}$ примеров, принадлежащих негативному классу для которых модель выдала вероятность $p$ (при этом $N_0(p)\,dp$ - число примеров негативного класса с вероятностями в интервале $[p,\,p+dp]$). Аналогично $n_{1}(p) = N_1(p)/\mathrm{pos}$ - доля примеров позитивного класса с вероятностями $p$:

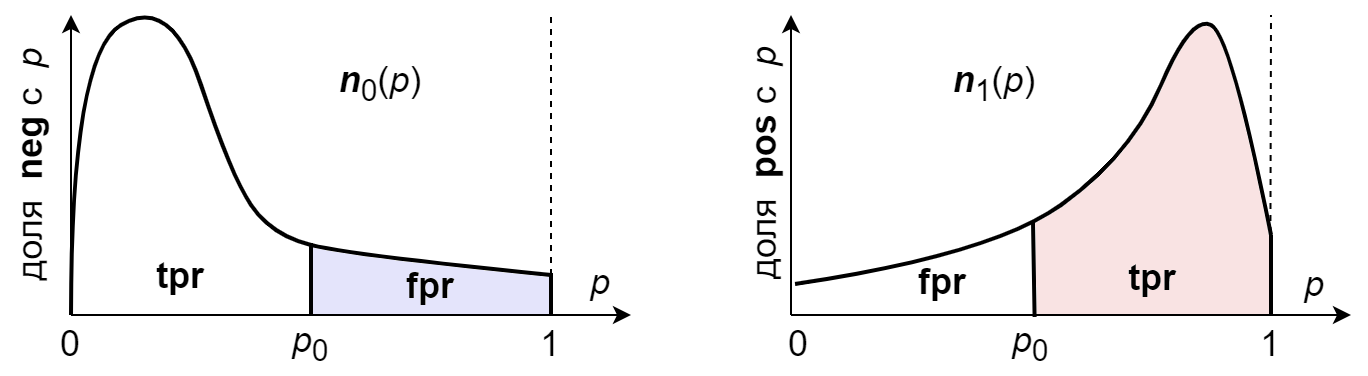
Величины $\mathrm{fpr}$ и $\mathrm{tpr}$ являются площадями под кривыми справа от пороговой вероятности $p_0$: $$ \mathrm{fpr}(p_0) = \int\limits^1_{p_0} n_0(p)\,dp,~~~~~~~~~~~~~~~\mathrm{tpr}(p_0) = \int\limits^1_{p_0} n_1(p)\,dp. $$

Если кривые одинаковые $n_0(p)=n_1(p)$ (т.е. предсказание не зависит от класса примера), то $\mathrm{fpr}=\mathrm{tpr}$, что на ROC-диаграмме соответствует пунктирной прямой, площадь под которой равна $\mathrm{auc}=1/2$.

Если $\mathrm{npr} \gt 1$ - простейшей моделью будет предсказание для любого примера негативного класса. В примере ниже при $\mathrm{npr} = 4$ такая модель будет иметь довольно высокую аккуратность, но auc будет всё равно равен 0.5 

                     acc  (tnr,   tpr)   pre   npr     auc
       80 |  0
cm =  --------       0.80 (0.80, 0.00)  0.00    4      0.5   
       20 |  0
Заметим, что для precision положено значение 0.0, хотя по определению имеем 0/0. Связано это с тем, что при вычислениях мы обычно добавляем малое число eps для устранения деления на ноль.

Чтобы для такого крайнего случая нарисовать ROC-кривую, следует считать, что вероятность негативного класса не строго равна нулю, а имеет узкий пик в окрестности нуля. Тогда следует, что tpr=fpt при любом $p_0$, т.е. ROC будет прямой, а auc=0.5

Пример на sklearn

Подключим библиотеки и сгенерим синтетический датасет "две луны" в котором есть два класса и два признака, характеризующих объекты (см. рисунок ниже): 

import numpy  as np
import matplotlib.pyplot as plt      

from sklearn.preprocessing  import StandardScaler 
from sklearn.utils          import compute_class_weight
from sklearn.metrics        import confusion_matrix, accuracy_score, 
from sklearn.metrics        import recall_score, precision_score
from sklearn.datasets       import make_moons

X, Y = make_moons(n_samples=1000, noise=0.2, random_state=42)
Вычислим отношение числа негативных и позитивных примеров (npr), выведем формы матриц и список классов (np.unique - список уникальных значений): 
npr = sum(Y==0)/sum(Y==1)                    
print(X.shape, Y.shape,  np.unique(Y), npr)  # (1000, 2) (1000,)  [0 1] 1.0
Нормируем данные таким образом, чтобы их среднее равнялось нулю, а дисперсия - единице. При помощи scaler в дальнейшем с теми же параметрами следует нормировать тестовые данные: 
scaler = StandardScaler().fit(X)    # затем используем и для теста
X = scaler.transform(X)             # (X-X.mean(0)) / X.std(0)
Затем, при помощи sklearn, получим веса классов для логистической регрессии и выполним собственно обучение: 
from sklearn.linear_model import LogisticRegression

w = compute_class_weight(classes=np.unique(Y), y=Y, class_weight ='balanced')

clf = LogisticRegression(C=1, class_weight={0:w[0],1:w[1]})
clf.fit(X,Y)
Вероятность в логистической регрессии достаточно условное понятие. Чем дальше точка от прямой в сторону позитивного класса, тем ближе "вероятность" к 1, а чем дальше в сторону негативного, тем ближе к 0. Значение предсказываемых классов вычисляем с порогом 0.5: 
probs = clf.predict_proba(X)[:,1]   # predict_proba [[P_neg=1-P_pos, P_pos]]
Y_pred = probs > 0.5                # номер класса

cm = confusion_matrix(Y, Y_pred)    #  [[435  65]
print(cm)                           #    [ 64 436]]

cm = confusion_matrix(Y, Y_pred, normalize='true') 
print(f"acc:{accuracy_score(Y,Y_pred):.3f} ({cm[0,0]:.3f},{cm[1,1]:.3f})")

Ниже на первой диаграмме выведены все обучающие примеры (красные точки - негативные, синие - позитивные). Прямая линия - разделяющая классы плоскость, полученная логистической регрессией. Заливка - степень уверенности модели. На второй диаграмме приведена ROC-диаграмма, значение auc и точка, соответствующая вероятности 0.5 На третей диаграмме приведено распределение вероятностей ($p=0$ - негативный класс, $p=1$ - позитивный):

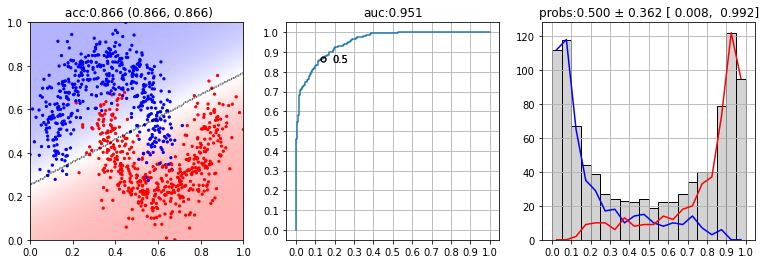
Для сравнения те-же данные в SVM-модели 
from sklearn.svm import SVC
clf = SVC(probability=True)

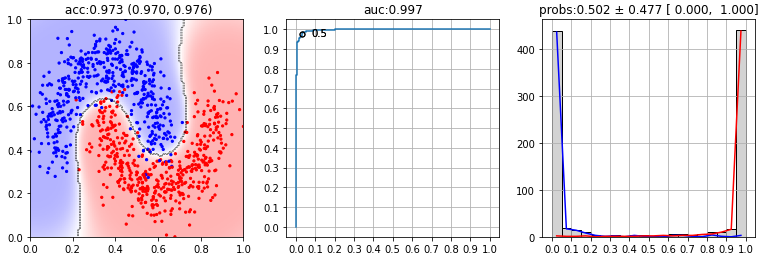
Вероятностный смысл auc

AUC равна вероятности того, что классификатор присвоит больший вес (вероятность) позитивному примеру, чем негативному (ранжирует случайный позитивный экземпляр выше, чем случайный негативный). Для доказательства этого важного утверждения, вычислим явным образом площадь под ROC-кривой (tpr как функция fpr):

$$ \mathrm{auc} = \int\limits^1_0 \mathrm{tpr}\,d\,\mathrm{fpr} = \int\limits^0_1 \mathrm{tpr}\,\frac{d\,\mathrm{fpr}}{dp}\, dp = -\int\limits^1_0 \mathrm{tpr}\,\frac{d\,\mathrm{fpr}}{dp}\, dp = \int\limits^1_0 \mathrm{tpr}(p)\,n_0(p)\, dp $$ В третьем равенстве изменён порядок интегрирования (со знаком минус). Затем учтено определение $\mathrm{fpr}(p_0)$, как интеграл от $n_0(p)$ c $p_0$ на нижнем пределе. Поэтому его производная по $p_0$ даст $n_0(p)$ со знаком минус. Далее подставим определение $\mathrm{npr}(p_0)$ через $n_1(p)$ и введём функцию $\Delta(x)$ равную 1, если логическое выражение $x$ истинно и 0 в противном случае: $$ \mathrm{auc} = \int\limits^1_0 \Bigr[ \int\limits^1_{p} n_1(p')\,dp'\Bigr]\,n_0(p)\, dp = \int\limits^1_0\int\limits^1_0 \Delta(p \lt p')~ n_0(p)\,n_1(p')\,\, dp\,dp'. $$

Множитель $n_0(p)\,n_1(p')\,\, dp\,dp'$ имеет смысл вероятности того, что случайно выбранный негативный пример имеет вес (вероятность) $p$, а случайно выбранный позитивный пример - вес $p'$. При помощи этого множителя усредняется $\Delta(p \lt p')$ что даёт среднее значение того что порядок весов негативного и позитивного примеров правильный ($p\lt p'$).

Процесс вычисления auc вероятностным методом можно представить следующим образом. Для наглядности, будем считать, что вероятности примеров негативного $p^{-}_i$ и позитивного $p^{+}_j$ классов упорядочены по возрастанию. В ячейке $(i,j)$ таблицы ставим $1$ если $p^{-}_i \lt p^{+}_j$ и 0, если $p^{-}_i \gt p^{+}_j$. Если ли же $p^{-}_i = p^{+}_j$, то будем ставить $0.5$ (можно считать что это не точное совпадение, а некоторые одинаковые узкие распределения вероятностей, правильный и неправильный порядки для которых равновероятны). Сумма чисел в ячейках, делённая на "площадь" $\mathrm{neg}\cdot\mathrm{pos}$ будет равняться $\mathrm{auc}$ (ниже первый рисунок):

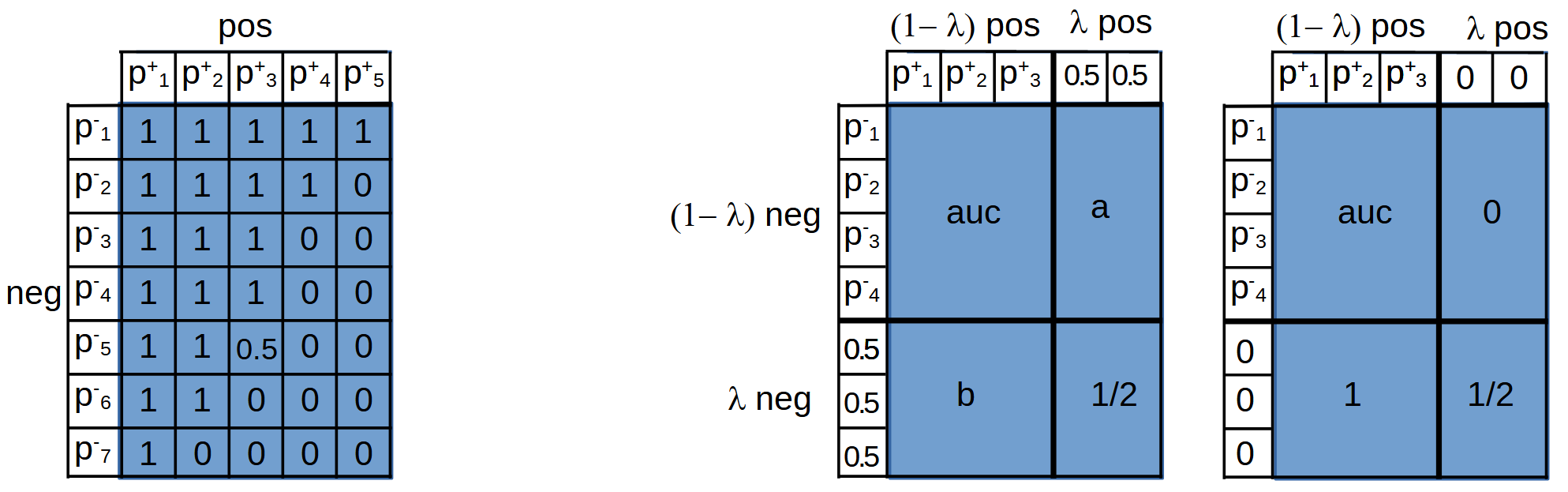
Рассмотрим случай, когда доля $\lambda$ всех примеров (как негативных, так и позитивных) в тестовых данных имеют свойства отличные от обучающих данных и по некоторому признаку мы можем их идентифицировать. Пусть на этих "плохих" данных модель работает заведомо неверно. Какие вероятности следует положить для плохих данных, чтобы максимизировать auc? Выше приведено два варианта: в первом - всем плохим данным присваивается вероятность $0.5$ и во втором вероятность $0$.

Если доля вероятностей негативных данных левее $p=0.5$ будет больше $0.5$, то auc между $1-\lambda$ хорошими негативными данными и плохими позитивными равен $a > 0.5$. Аналогично для $b > 0.5$. Поэтому выгоднее положить для вероятностей плохих данных значение $0.5$:

$$ \mathrm{auc}~~ \mapsto~~ (1-\lambda)^2\,\mathrm{auc} + \lambda\,(1-\lambda)\,(a+b) + \lambda^2/2 ~~>~~ (1-\lambda)^2\,\mathrm{auc} + \lambda\,(1-\lambda) + \lambda^2/2 $$

При помощи вероятностной интерпретации метрики auc, можно написать следующую функцию для её вычисления: 

def auc(y_true, probs):
    x = probs[y_true == 0]                 # negative class probabilities
    y = probs[y_true == 1]                 # positive class probabilities
    z = np.array([np.tile  (x, len(y)),    # x0,x1,...x0,x1,...    
                  np.repeat(y, len(x))])   # y0,y0,y0,...,y1,y1,,    
    z = z.T                                # [x0,y0], [x0,y1], ..., [xn,ym]
    
    a = np.zeros_like(z)
    a[z[:,0] <  z[:,1]] = 1.0
    a[z[:,0] == z[:,1]] = 0.5

    return a.mean()

Разное

Лосс-функция, максимизирующая непосредственно auc может выглядеть следующим образом: 

def loss(y_true, y_pred):
    """ 
    y_true: (N,) - номера классов {0,1}  
    y_pred: (N,) - выход моделе для каждого примера (вероятности)
    """
    y_t = torch.cartesian_prod(y_true, y_true)
    y_p = torch.cartesian_prod(y_pred, y_pred)              
    
    L   = (y_t[:,0]-y_t[:,1]) * (y_p[:,1]-y_p[:,0])
    
    return 0.5 + L.mean()