Метод главных компонент (PCA)

Введение

Часто n-мерное пространство признаков оказывается избыточным. Объекты (точки) концентрируются в нём на вложенных m-мерных поверхностях, где m существенно меньше n. Выявление таких поверхностей приводит к снижению размерности задачи и упрощению дальнейшего анализа данных (в задачах классификации и т.п.). Метод главных компонент (principal component analysis) является простейшим методом, в котором, в качестве m-мерной поверхности выступает m-плоскость.

Напомним, что $m$ векторов $\mathbf{e}_k=\{\mathbf{e}_1,...,\mathbf{e}_m\}$ задают уравнение $m$-плоскости в $n$-мерном пространстве: \begin{equation}\label{plane_eq} \mathbf{x}= \mathbf{x}_0 + \sum^m_{k=1} t_k\mathbf{e}_k. \end{equation} Параметры $\{t_1,...,t_m\}$ выступают декартовыми координатами в базисе $\{\mathbf{e}_1,...,\mathbf{e}_m\}$ (если он ортогонален). Вектор $\mathbf{x}_0$ задаёт положение начала координат (точка в которой все координаты на плоскости $t_k$ равны нулю). Если $m=1$, то (\ref{plane_eq}) будет уравнением прямой (одномерный объект). При $m=2$ мы имеем двумерную плоскость и т.д.

Квадрат кратчайшего евклидового расстояния $d^2=(\mathbf{X}-\mathbf{x})^2$ от произвольной точки $\mathbf{X}$ до $m$-плоскости (\ref{plane_eq}) равен: \begin{equation}\label{d2_to_plane} d^2 = \bigr(\mathbf{X}-\mathbf{x}_0\bigr)^2 - \sum^m_{k=1} \bigr[(\mathbf{X}-\mathbf{x}_0)\,\mathbf{e}_k \bigr]^2, \end{equation} а проекция точки $\mathbf{X}$ на $m$-плоскости имеет следующие координаты (в $n$- и $m$- пространствах): \begin{equation}\label{projec_coord} \mathbf{X} ~\mapsto~\mathbf{x}=\mathbf{x}_0 + \sum^m_{k=1} \bigr[(\mathbf{X}-\mathbf{x}_0)\,\mathbf{e}_k\bigr]\mathbf{e}_k, ~~~~~~~~~~~~~ t_k = (\mathbf{X}-\mathbf{x}_0)\,\mathbf{e}_k. \end{equation}

Центр тяжести

В методе главных компонент ищут $m$-плоскость, сумма квадратов расстояний от которой до множества точек (обучающий набор объектов) $\mathbf{X}_1,...,\mathbf{X}_N$ минимальна (нижний индекс - номер объекта). Будем в дальнейшем обозначать угловыми скобками усреднение по всем точкам. Например, среднее значение (центр тяжести $N$ объектов) равен: $$ \langle \mathbf{X} \rangle = \frac{1}{N}\sum^N_{i=1} \mathbf{X}_i. $$ Таким образом, мы требуем, чтобы $$ \langle d^2 \rangle = \langle\bigr(\mathbf{X}-\mathbf{x}_0\bigr)^2\bigr\rangle - \sum^m_{k=1} \bigr\langle\bigr[(\mathbf{X}-\mathbf{x}_0)\,\mathbf{e}_k \bigr]^2\bigr\rangle = \min. $$ Определим сначала $\mathbf{x}_0$. Беря производную по $\mathbf{x}_0$ и приравнивая её нулю, имеем: $$ \langle\mathbf{X}-\mathbf{x}_0\rangle - \sum^m_{k=1} \bigr[(\langle\mathbf{X}\rangle-\mathbf{x}_0)\,\mathbf{e}_k \bigr]\,\mathbf{e}_k = 0. $$ Это соотношение тождественно выполняется, если $\mathbf{x}_0=\langle\mathbf{X}\rangle$, т.е. плоскость проходит через центр тяжести. Поэтому вычтем его из каждой точки: $\mathbf{X}_i \mapsto \mathbf{X}_i - \langle \mathbf{X} \rangle$ и далее будем считать, что $\langle \mathbf{X} \rangle=0$ и $\mathbf{x}_0=0$.

Первый компонент

Для определения направляющих векторов $\mathbf{e}_1,...,\mathbf{e}_m$ (базис в плоскости) необходимо найти максимум (знак минус в (\ref{d2_to_plane})!) выражения: \begin{equation}\label{maxD} D = \sum^m_{k=1} \bigr\langle\bigr(\mathbf{X}\,\mathbf{e}_k \bigr)^2\bigr\rangle = \bigr\langle\bigr(\mathbf{X}\,\mathbf{e}_1 \bigr)^2\bigr\rangle+...+\bigr\langle\bigr(\mathbf{X}\,\mathbf{e}_m \bigr)^2\bigr\rangle = \max,~~~~~~~~~~~\mathbf{e}_k\mathbf{e}_p = \delta_{kp}, \end{equation} при сохранении ортонормированности векторов. Максимальным должно быть каждое слагаемое в сумме. Чем больше значение слагаемого, тем более значимым является $k$-й вектор. Пусть эти слагаемые отсортированы по убыванию значимости. Определим сначала $\mathbf{e}_1$, который называют первым компонентом. В плоскости он может иметь произвольное направление (произвол ориентации базиса в плоскости). Поэтому стоит задача поиска максимума $\bigr\langle\bigr(\mathbf{X}\,\mathbf{e}_1 \bigr)^2\bigr\rangle$ при условии, что $\mathbf{e}^2_1=1.$ Эту задачу можно решать методом множителей Лагранжа: \begin{equation}\label{max_eqX} \bigr\langle\bigr(\mathbf{X}\,\mathbf{e}_1 \bigr)^2\bigr\rangle + \lambda\,(1-\mathbf{e}^2_1) = \max. \end{equation} Беря производные по $\mathbf{e}_1$, $\lambda$ и приравнивая их нулю, имеем: \begin{equation}\label{e1} \bigr\langle\bigr(\mathbf{X}\,\mathbf{e}_1 \bigr)\mathbf{X}\bigr\rangle = \lambda\,\mathbf{e}_1,~~~~~~~~~~~~~\mathbf{e}^2_1 = 1. \end{equation} Обозначим в круглых скобках номер компоненты вектора в $n$-мерном пространстве: $\mathbf{e}_1=\{e^{(1)}_1,...,e^{(n)}_1\}$. Первое уравнение переписывается в форме уравнения на собственные значения: \begin{equation}\label{eq_Ce} \sum^n_{j=1}C_{ij}\,e^{(j)}_1 = \lambda\,e^{(i)}_1 \end{equation} ковариационной матрицы: \begin{equation}\label{eq_cov} C_{ij} = \langle X^{(i)}X^{(j)}\bigr\rangle = \frac{1}{N-1}\sum^N_{k=1} X^{(i)}_kX^{(j)}_k. \end{equation}

Из (\ref{e1}) следует (умножаем первое соотношение на $\mathbf{e}_1$), что $\lambda=\bigr\langle\bigr(\mathbf{X}\,\mathbf{e}_1 \bigr)^2\bigr\rangle$, поэтому из всех собственных значений необходимо выбрать максимальное. Впрочем, это не обязательно. Если будут найдены все собственные значения матрицы $C_{ij}$ (см. ниже), то их можно отсортировать в порядке убывания, оставив только $m$ самых больших. Соответствующие им собственные векторы ковариационной матрицы и являются искомыми направляющими векторами $m$-плоскости.

Второй компонент

Пусть первый компонент $\mathbf{e}_1$ и первое собственное значение $\lambda_1=\lambda$ матрицы $C_{ij}$ уже найдены. Изменим координаты точек следующущим образом: \begin{equation}\label{tranform} \mathbf{X}' = \mathbf{X} - (\mathbf{X}\mathbf{e}_1)\,\mathbf{e}_1,~~~~~~~~~\mathbf{X}'\mathbf{e}_1=0. \end{equation} Среднее значение останется нулевым $\langle\mathbf{X}'\rangle=0$. Остаток максимизируемой суммы (\ref{maxD}) также не поменяется: $$ D' =\bigr\langle\bigr(\mathbf{X}\,\mathbf{e}_2 \bigr)^2\bigr\rangle+...+\bigr\langle\bigr(\mathbf{X}\,\mathbf{e}_m \bigr)^2\bigr\rangle =\bigr\langle\bigr(\mathbf{X}'\,\mathbf{e}_2 \bigr)^2\bigr\rangle+...+\bigr\langle\bigr(\mathbf{X}'\,\mathbf{e}_m \bigr)^2\bigr\rangle =\max. $$ Его необходимо продолжать максимизировать. Заметим, что пересчитывать ковариационную матрицу (\ref{eq_cov}) по всем точкам $\mathbf{X}'$ не обязательно, так после преобразования (\ref{tranform}) она меняется следующим образом: $$ C'_{ij} = C_{ij} - \sum^{n}_{k=1} C_{ki}\, e^{(k)}_1e^{(j)}_1 - \sum^{n}_{k=1} C_{kj}\, e^{(k)}_1e^{(i)}_1 + \sum^{n}_{k=1} C_{kp}\, e^{(k)}_1e^{(p)}_1 \,e^{(i)}_1e^{(j)}_1. $$ Учитывая уравнение на собственные значения (\ref{eq_Ce}) это соотношение можно упростить: \begin{equation} C'_{ij} = C_{ij} - \lambda_1 \, e^{(i)}_1e^{(j)}_1. \end{equation} Теперь процесс поиска максимума можно повторять до тех пор, пока все векторы базиса плоскости не будут найдены. При этом, в силу построения по формуле (\ref{tranform}), все эти векторы окажутся ортогональными.

Несложно видеть, собственные значения матрицы $C'_{ij}$ одновременно являются собственными значениями исходной матрицы $C_{ij}$. Поэтому $m$-плоскость строиться по $m$ собственным векторами ковариационной матрицы, соответствующим максимальным собственным значениям.

Ещё одна интерпретация собственных векторов ковариационной матрицы - это оси эллипсоида характерного "разброса" точек в пространстве. Если эллипсоид вытянут вдоль одной из осей - это главная (наиболее значимая) компонента. Следующая по "вытянутости" ось - вторая компонента и т.д.

Пример 1: ирисы Фишера

Рассмотрим в качестве примера набор из 150 измерений длины и ширины лепестков цветков ириса (ирисы Фишера). В данном случае пространство признаков 4-мерно и в задаче классификации присутствуют 3 класса.

Статистики по всем признакам имеют вид: 

xi     aver    sigma    min     max
x1    5.843   0.828   4.30    7.90
x2    3.054   0.434   2.00    4.40
x3    3.759   1.764   1.00  6.90
x4    1.199   0.763   0.10  2.50
После нормировки $x_i \mapsto (x_i-\langle x_i\rangle)/\sigma_i$ ковариационная матрица $C_{ij}$ равна: 
 1.000  -0.109   0.872   0.818
-0.109   1.000  -0.421  -0.357
 0.872  -0.421   1.000   0.963
 0.818  -0.357   0.963   1.000
Её собственные значения и собственные векторы: 
λ1=2.911;   e1=(-0.522,  0.263, -0.581, -0.566)
λ2=0.921;   e2=(-0.372, -0.926, -0.021, -0.065)
λ3=0.147;   e3=( 0.721, -0.242, -0.141, -0.634)
λ4=0.021;   e4=(-0.262,  0.124,  0.801, -0.524)

Главная компонента (наибольшее собственное значение λ1=2.911) cущественно отличается от остальных. Это свидетельствует о том, что точки в 4-мерном пространстве в основном вытянуты вдоль прямой. Следующее по значимости собственное значение λ2=0.921 и соответствующий ему собственный вектор e2, вместе с вектором e1 образует двумерную плоскость. Справа на рисунке приведена проекция данных на эту плоскость в диапазоне [-4,..,4] по каждой координате. Вектор $\mathbf{e}_1$ направлен вправо, а $\mathbf{e}_2$ - вниз. Статистики координат на этой плоскости имеют вид: 

ti     aver   sigma      min    max
t1   0.000   1.706   -3.298  2.765
t2   0.000   0.960   -2.713  2.649
Синие круги - первый класс, красные - второй и зелёные - третий.

Пример 2: рукописные цифры MNIST

База рукописных цифр MNIST содержит содержит 60000 обучающих 10000 тестовых изображений 28x28 пикселей в градациях серого. Все картинки отцентрованы по центру тяжести и более или менее приведены к единому масштабу.

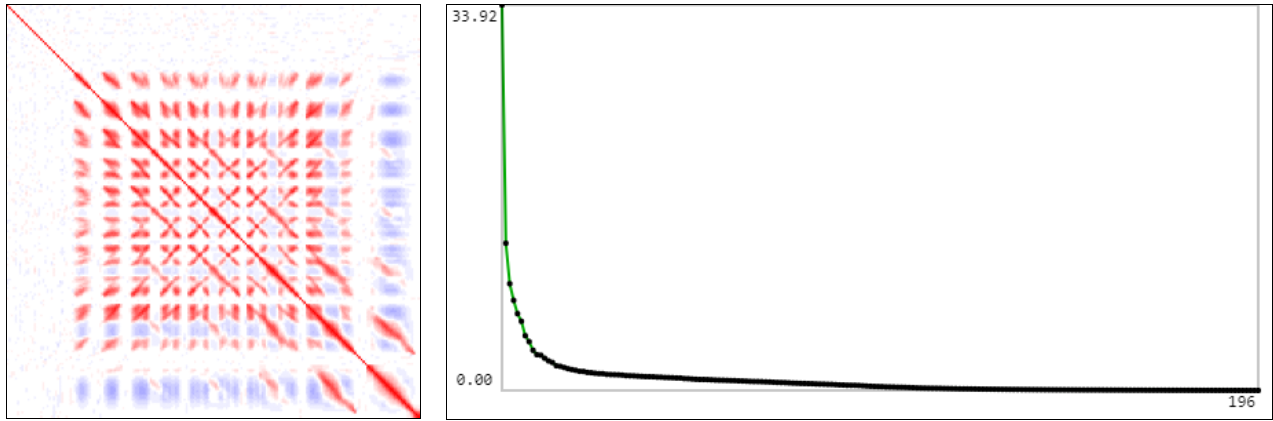
Уменьшим цифры в 2 раза (картинки 14×14) и посчитаем ковариационную матрицу (в её графическом представлении красный цвет +1, синий -1). Собственные значения ковариационной матрицы приведены справа от неё. Видно, что размерность пространства признаков существенно меньше чем 14·14=196

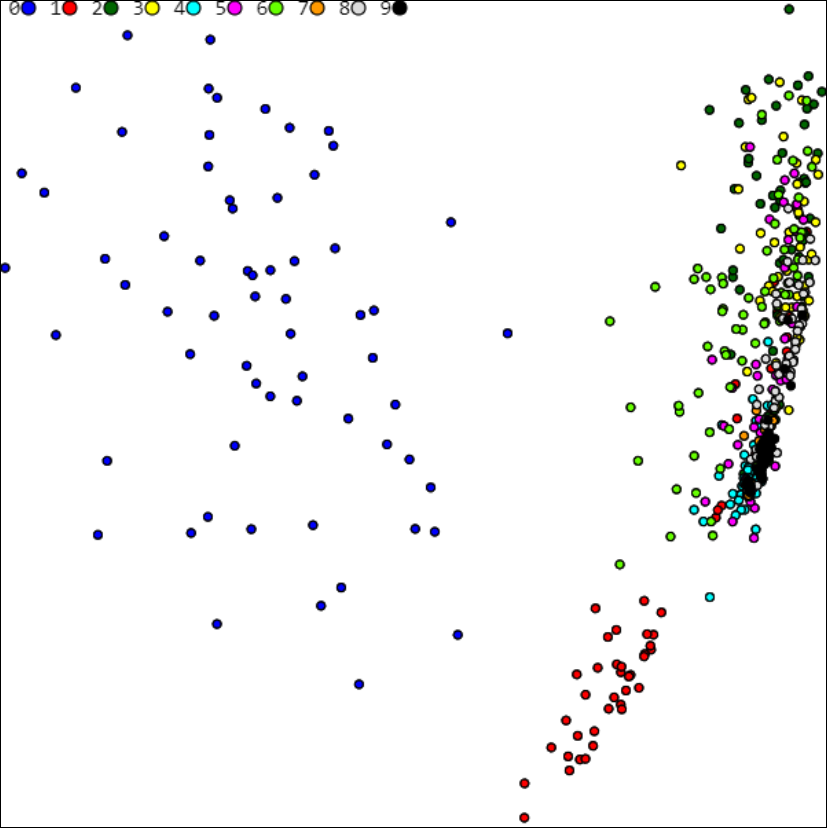
PCA 2-мерная ($m=2$) плоскость для MNIST имеет вид (цветом помечены различные классы=цифры, расшифровка которых приведена в верхней части рисунка):

Проблемы PCA в задачах классификации

Метод главных компонент позволяет выяснить характерную размерность данных, т.е. размерность поверхности, вложенной в пространство признаков. Однако, проектирование данных на эту $m$-мерную плоскость может существенно ухудшить классификацию классов. Справа на рисунке приведены два класса (круги и крестики). Они являются хорошо (линейно) разделимыми. Однако при проектировании на линию (одна главная компонента), объекты различных класов перемешаются и перестанут быть разделимыми.

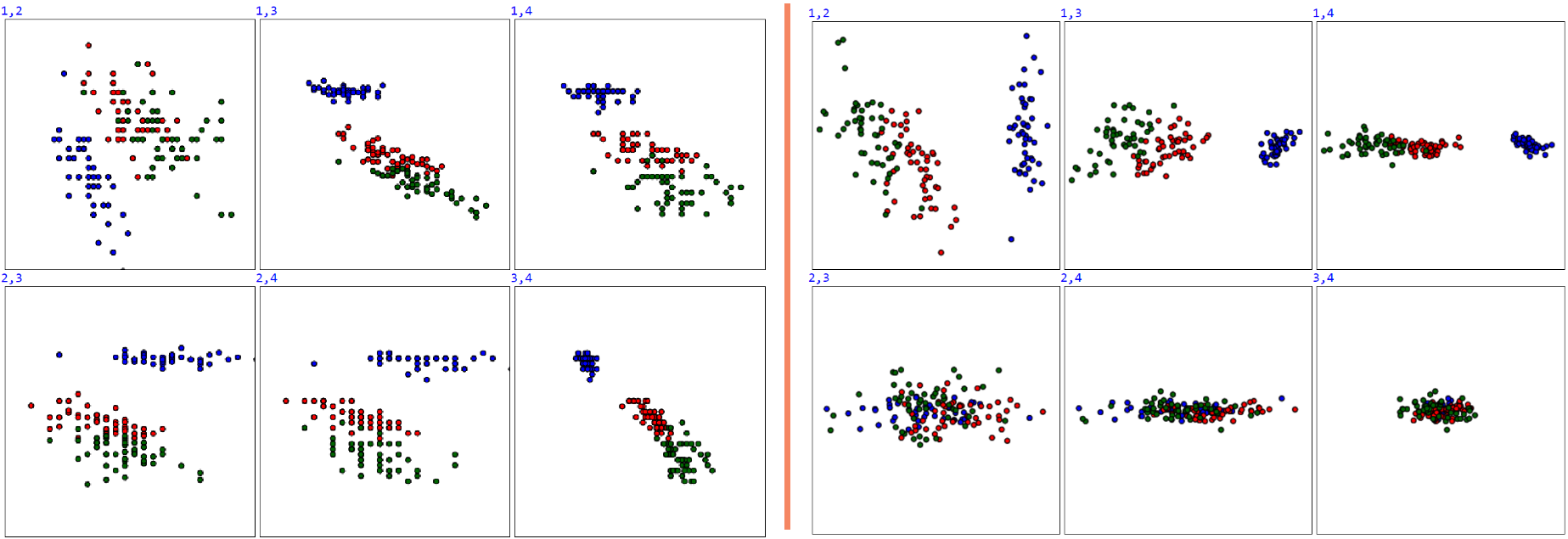
Например, в задаче ирисов Фишера метод главных компонент свидетельствует о "двумерности" исходных данных. Однако, первая главная компонента направлена не в направлении наиболее значимого (четвёртого) признака. Ниже, слева от вертикальной линии приведены исходные данные ирисов Фишера во всех парах координат. Справа те-же данные после устранения корреляции (т.е. PCA c $m=4$):

Ещё одна очевидная проблема связана с грубостью линейного приближения. Если объекты расположены не вдоль линии или плоскости, а вдоль некой изогнутой поверхности, метод главных компонент может вводить в заблуждение.