DemonScript: Работа с графами

Введение

Граф является одним из базовых типов DemonScript. Графы состоят из узлов. Любая пара узлов может быть соединена направленным ребром одного из заданных типов. С каждым ребром связывается нечёткое логическое значение.

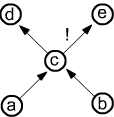
В задачах искусственного интеллекта узлы графа, обычно, являются конкретными объектами (Её_кот, Moя_подруга_Мия) или абстрактными классами объектов (животное, контейнер). Рёбро - это бинарное отношение между двумя объектами, имеющее то или иное логическое значение. Например, следующий граф:

является представлением фразы "Мия взяла ящик без крышки, в котором находился большой чёрный кот", дополненной "обыденными знаниями" (cat isa animal). Все рёбра здесь имеют истинное значение (True), кроме отношения box has lid, которое ложно (False), что помечается восклицательным знаком перед именем отношения. Если два узла не связаны ребром, то отношение между ними считается неопределённым (Undef).

Типы рёбер

Типы возможных рёбер объявляются при помощи оператора edges, который должен стоять до его использования. Объявленные типы рёбер доступны в любом графе скрипта. Имя ребра может начинаться с символа @:

edges in, @above, on

Существует ряд предопределённых рёбер, которые объявлять не надо:

X isa Y	: X - экземпляр класса Y или его подмножество (Барбос isa собака, собака isa животное)
X sub Y	: Y - субъект действия X (take sub Mia)
X obj Y	: Y - объект действия X (take obj box)
X has Y	: Y - часть объекта X (box has lid)
X attr Y	: Y - атрибут объекта X (cat attr black)

В DemonScript существует предопределённая переменная GRAPH. Она является текущим графом с которым работают функции добавления узлов, задания или чтения рёбер. Список всех доступных типов рёбер (отношений) в виде массива можно получить при помощи метода графа edges():

out GRAPH.edges()         //> [isa, sub, obj, has, attr, in, @above, on]

Именованные узлы

Узлы графа могут иметь имена или быть безымянными. Именованные узлы объявляются при помощи оператора nodes. Он может встречаться в любом месте скрипта произвольное число раз и объявляемые в нём узлы добавляются в текущий граф. Имя узла может начинаться с символа доллара $.

nodes a, b                         // в граф добавились два узла а и b
nodes c, $cat                      // в граф добавились ещё два узла

out GRAPH.type()                   //> graph (тип переменной)
out GRAPH.size()                   //> 4     (число узлов)
out $cat                           //> $cat
out GRAPH                          // выводим граф на экран

   GRAPH {
      a {}, b {}, c {}, $cat {}
   }

Безымянные узлы

При помощи методов графа .add_node() и .add_nodes(N) можно создавать безымянные узлы:

GRAPH.delete_nodes()               // удаляем все, созданные ранее узлы

GRAPH.add_nodes(9)                 // добавляем в граф 9 узлов
GRAPH.add_node()                   // добавляем ещё один узел

out GRAPH.size()                   //> 10 (в графе 10 узлов)

К безымянным узлам можно получить доступ по индексу, начиная с единицы. Например GRAPH[4] - это 4-й узел графа. К именованным узлам также можно обращаться по номеру, который присваивается в порядке их объявления оператором nodes:

nodes a                            // добавили ещё один узел
out a.id()                         //> 11 - индекс узла
out GRAPH[11]                      //> a (11-й узел графа именован)

При добавлении узла методом .add_node() можно сразу получить ссылку на этот узел. Кроме этого, можно задать его имя, которое появляется при выводе графа оператором out. Если узел с таким именем уже есть, к его имени добавится цифра:

var N = GRAPH.add_node("aa")
out N                              //> aa (12-й узел графа)

Задание отношений

С ребром между двумя узлами связывается логическое значение:

edges in, on                       
nodes a, b, c, d                   // граф с 4-я именованными узлами

a  in b;                           // ребро a in b - истинно
b !in a;                           // ребро b in a - ложно
a  in GRAPH[4]                     // ребро между "а" и 4-м узлом "d" 

Когда пишется выражение a in b; это означает создание ребра от узла "a" к узлу "b" и присваивание этому ребру истинного значения True. Запись b !in a; - это создание ребра с ложным значением False. Такой же результат можно получить следующим образом:

a in b = a in d = True             // a  in b; a in d; 
b in a = False                     // b !in a
a on c = (0.2, 0.8)                // нечёткое истинностное значение

a in [b, d];

a in [b, d, !c];

Если отношение вызывается в выражении, получается логическое значение ребра: а его чтение:

var V = a in b;                    //> V = True         
out V, b in a;                     //> True, False

Вывод структуры графа

Существует несколько различных форматов, в которых может быть выведена структура графа. Например, оператор out выводит граф в форме "json"-подобной структуры :

   GRAPH {
      a {  in: [b,4] },
      b {  in: [!a]  },
      c {},
      4 {}   
   }

При помощи метода GRAPH.dot("file.dot"), граф сохраняется в файле в dot-формате. Этот файл затем можно обработать утилитой из пакета GraphViz, чтобы получить графическое представление графа.

Циклы по узлам

Создадим граф c 5-ю узлами и единственным типом рёбер (отношением) @r:

edges @r
nodes a,b,c,d,e

[a, b] @r c;     c @r [d, !e] 

Для прохода по всем узлам графа используется цикл for (переменную X объявлять не надо):

for X :
   out X                           //> a b c d e

for X in X @r c:
   out X                           //> a,b

Аналогично получается список всех выходящих из узла "c" узлов по ребру @r с логическим значением False:

for X in  (с @r X) == False :
   out X                           //> e

Если необходимо вывести все объекты, связанные ребром @r, независимо от его логического значения (отличного от неопределённого Undef), то используется функция X.is_edge(E, Y):

for X in c.is_edge(@r, X) :
   out X, "(",, c @r X,, "),",     //> d (True), e (False)

Кванторы exists и forall

Функция exists (существует) даёт первый узел, удовлетворяющий условию:

if exists(X, X @r c):              // найти X который находится в b
   out X                           //> a 
else
   out "Not exists"

Можно указать число объектов, которых в должно в точности существовать. Для этого служит третий параметр функции exists. В этом случае в переменной X оказывается массив с перечнем узлов "которые существуют":

if exists(X, X @r c, 2):
   out X                           //> [a,b]

Аналогична функция forall(X, COND), которая возвращает True, если условие COND, зависящее от X, выполняется для всех узлов графа.

Если в кванторных функциях или циклах стоит значение ребра X E Y, то они работают достаточно быстро (как для входящих, так и для исходящих рёбер). Однако, для произвольного условия, чтобы выяснить его истинность, перебираются все узлы графа. Поэтому в случае больших графов это может занять некоторое время.

Непосредственно получить узлы, в которые из данного узла X следуют рёбра типа E, можно при помощи метода X.nodes(E). При этом логические значения рёбер роли не играют. Вторым аргументом этого метода можно указать конкретное логическое значение. Тогда будут получены узлы, соединённые ребром с этим значением:

out c.nodes(@r);                   // [d, e]
out c.nodes(@r, False);            // [e]

Путь на графе

При работе с графом доступны различные алгоритмы. Рассмотрим граф, описывающий несколько вложенных друг в друга ящиков:

edges in                            // типы рёбер       
nodes a, b, c, d                    // добавляем узлы

c in d;                             // с внутри d
[a, b] in c;                        // a и b внутри с

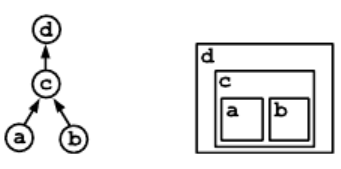
   GRAPH {
      a { in:[c] },
      b { in:[c] },
      c { in:[d] },
      d {}
   }

out a.path(in, d)                  // есть ли путь из a в d > True
out a.path(in, b)                  // есть ли путь из a в b > Undef

Аналогично, при помощи функции X.common(E, Y) можно выяснить, существует ли общий узел, в которой можно попасть, двигаясь из узлов X, Y по рёбрам типа E. На древесном графе, подобном приведенному выше, это означает, что X, Y имеют общего предка:

out a.common(in, d)                // есть ли предок у a и d > True
out a.common(in, b)                // есть ли предок у a и b > True

Создание графов

Создавать графы можно двумя способами: при помощи конструктора GRAPH() и метода .copy(). В первом случае создаётся пустой граф, а во втором создаётся граф, в который копируются все узлы и рёбра того объекта, у которого вызван метод .copy(). В качестве аргумента в конструктор и метод .copy() можно передавать строку (тестовое имя графа), которая будет появляться при выводе графа оператором out. Это имя можно получить методом A.name(). Этот же метод позволяет переименовать граф: A.name("new A").

edges in
nodes a, b                         // эти узлы попали в GRAPH

var A = GRAPH.copy("A")            // это копия, содержащая a,b
var B = GRAPH("B")                 // создаём пустой граф
var C = B.copy("C")                // это копия пустого графа B

out A,B,C

   A { a {}, b {} }
   B { }
   C { }

Каждому графу, который создаётся при помощи конструктора, присваивается уникальное целое число (номер класса). Копия графа, созданная по .copy(), унаследует номер класса родительского графа. Все графы одного класса имеют одинаковые узлы (но, возможно, различные рёбра). У графов разных классов имена узлов не должны пересекаться. Выше граф A принадлежит одному классу, а графы B,C к другому, т.к. B создан конструктором, а С - его копия.

Установим граф B в качестве текущего. Для этого его необходимо присвоить в переменную GRAPH:

GRAPH = B                          // текущим будет граф B
nodes c, d                         // в него добавляем два узла

C.nodes e                          // добавляем в граф С и все графы его класса узел e
e in d;                            // задаём ребро в графе B
C=>d in C=>e;                      // задаём ребро в графе С

   
   A { a {},   b {}        }
   B { c {},   d {},        e { in:[d] } }
   C { c {},   d { in:[e]}, e { } }

Граф A все эти манипуляции с графми B и С не заметил, так как принадлежит к другому классу. Номер класса можно получить при помощи функции class_id:

out A.class_id()                   //> 0
out B.class_id(), C.class_id()     //> 1,1

Таким образом, все графы разбиваются на классы, каждый из которых характеризуется уникальным номером. Графы одного класса имеют одинаковые узлы. Добавление в любой граф данного класса узлов приводит к добавлению этих же узлов во все графы этого класса. Модификация рёбер графов одного или разных классов происходит независимым образом.

Ссылки на графы

При присвоении переменных типа graph не происходит копирования данных, а передаётся лишь ссылка ("указатель") на эти данные. Это быстрая операция. Рассмотрим подробнее, что при этом происходит.

Создадим две переменные типа graph, которые будут хранить независимые копии графа GRAPH:

edges in
nodes a, b, c                      // эти узлы попали в GRAPH

var A = GRAPH.copy("A")            // одна   копия графа GRAPH
var B = GRAPH.copy("B")            // вторая копия графа GRAPH

GRAPH = B                          // текущий граф ссылается на B
b in c;                            // меняем ребро в графе B

out A, B

   A     { a{ },  b{},         c{} }
   B     { a{ },  b{ in:[c] }, c{} }

Если теперь сделать текущим граф A:

GRAPH = A
out GRAPH

  A     { a{ },  b{},         c{} }

Таким образом, при простом присваивании графов: G1=G2 происходит запоминание в переменной G1 ссылки на данные графа G2. Любые изменения с этими данными "почувствуют" обе переменные G1,G2. Если же присвоение делать при помощи метода copy(), то данные становятся независимыми, и их изменение в одном графе, другой не "почувствует" (за исключением добавления узлов, так как это графы одного класса).

Хранение значений в узлах

Любой узел графа может в себе сохранять данные одного из базовых типов. Для чтения и записи значения служит метод value. Задаваемое значение передаётся аргументом в этот метод, а вызов метода без аргумента - возвращает значение:

nodes a, b, c;

a.value(True)                      // узел "a" хранит логическое значение
b.value(3.14)                      // узел "b" хранит число
c.value([1,1,2,3,5])               // узел "c" хранит массив

out a.value(),b.value(),c.value()  // True, 3.14, [1,1,2,3,5]

Контроль значений рёбер

При смене логического значения уже существующего ребра, DemonScript выводит предупреждение. Чтобы его ликвидировать, необходимо вызвать метод графа verbose со значением 0:

nodes a,b
GRAPH.verbose(0)                   // подавляем предупреждения

a isa  b;                          // отношение истинно
a !isa b;                          // отношение ложно 

GRAPH.verbose(1)                   // включаем предупреждения

a isa  b;                          // ребро поменялось - будет предупреждение

GRAPH.locked(1)                    // запрет смены значения рёбер

При копировании графа методом .copy(), значения verbose и locked также копируются. Однако затем у копии их можно независимым образом поменять.