DemonScript: Города и дороги

Постановка задачи

Рассмотрим N городов. Любая пара городов может быть соединена дорогой с двухсторонним движением. Автомобильная карта описывается графом. Его узлами являются города, а ненаправленными рёбрами - дороги. Введём два отношения:

Как обычно, нас интересует логический вывод в условиях неполноты информации. Будем предполагать, что число узлов фиксировано, т.е. все города известны (замкнутость мира). Рёбра описываются трёхзначной логикой: True, False и Undef. Если ребро есть, то отношение X @r Y равно True. Если известно что ребра нет, отношение равно False. Наконец, если ребро не задано (Undef), это означает, что пока нет информации о его наличии или отсутствии (может оказаться как True, так и False).

Пусть есть следующие 4 карты (графа):

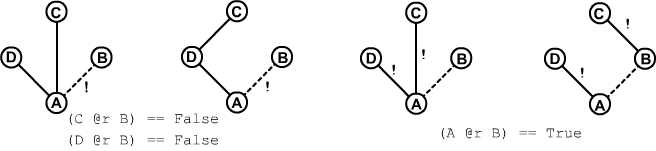
В первом примере известно, что есть прямые дороги A-D и A-C (отношение @r рисуем сплошной линией). Есть ли дороги С-D, С-B или D-B не известно (ребра не нарисованы). Но утверждается, что пути между A-B нет, что помечает восклицательный знак у пунктирного ребра (это отношение @p). Если ребро C-B типа @r есть, то появляется путь из A в B, через узел C. Отсюда делаем вывод, что (C @r B) == False. Аналогично (D @r B) == False и, конечно, (A @r B) == False. Подобным образом проводятся рассуждения в остальных примерах.

Аксиомы для X @r Y

Определим в DemonScript типы рёбер и зададим базовые аксиомы, описывающие отношение X @r Y: 

edges @r, @p                       // типы рёбер

Mind.add(
  !(X @r X),                       // (1) антирефлексивность
   (X @r Y) -> (Y @r X) )          // (2) симметричность
Первая аксиома антирефлексивности означает, что в узлах нет петель (рёбер @r начинающихся и заканчивающихся на одном и том же узле). Вторая аксиома требует симметричности рёбер: если из X идёт ребро в Y, то и из Y идёт ребро в X (граф с ненаправленными рёбрами).

C помощью этих аксиом можно посчитать число возможных графов с данным числом узлов. Напомним, что любой граф полностью определяется матрицей смежности. В ней, на пересечении i-й строки и j-той колонки стоит 1, если от узла i к узлу j ведёт ребро и 0, если его нет. Для ненаправленного графа без петель эта матрица симметрична и имеет нули на диагонали. Поэтому для n узлов матрица смежности имеет n(n-1)/2 независимых элементов. Отсюда следует, что существует 2n(n-1)/2 различных графов с пронумерованными узлами (это количество бинарных чисел с n(n-1)/2 разрядами). "Воспроизведём" этот результат численно на DemonScript: 

GRAPH.add_nodes(5)                 // создаём граф с 5 узлами

out Mind.count_models(GRAPH, @r)   // подсчитываем число моделей
Метод .count_models объекта Mind подсчитывает все возможные модели не противоречащие аксиомам. При этом, для каждого неопределённого (Undef) ребра типа @r (второй аргумент метода) порождается две копии графа GRAPH (первый аргумент метода). У одного графа ребро устанавливается в True, у второго - в False. С этими графами запускается логический вывод, который, в соответствии с новой информацией, по аксиомам устанавливает другие рёбра (фактически срабатывает только аксиома симметричности). Процедура повторяется для каждого графа (в глубину), пока не получится полностью определённый граф у которого заданы все рёбра @r. Выше оператор out на экран выведет 1024. Реализацию подобного алгоритма на DemonScript можно найти в документе размещения ящиков.

Функция path

Пусть у графа заданы только рёбра @r (в True или False). Тогда для выяснения истинности отношения X @p Y можно воспользоваться функцией X.path(@r, Y). Рассмотрим, например, граф из 9 узлов на левой картинке ниже. Три ребра (1-7, 7-6 и 6-8) имеют явный запрет (False). Ещё 7 рёбер истинные (True). Информации об остальных 26 дорогах нет (Undef):

Создадим этот граф при помощи DemonScript: 

var G = GRAPH()                       // создаём пустой граф конструктором
G.add_nodes(9)                        // добавляем 9 не именованных узлов

var EdgesF = [ [1,7], [6,7], [6,8] ]
var EdgesT = [ [1,2], [2,3], [3,4], [3,6], [4,5], [4,6], [4,8] ]

for E in EdgesT: G[E[0]] @r G[E[1]] = True
for E in EdgesF: G[E[0]] @r G[E[1]] = False

Mind.set_graph(G)                     // восстанавливаем все рёбра
G.dot("c.dot", [@r], False)           // выводим без петель в dot-формате

В массив EdgesF помещены номера узлов, соединенные ложными рёбрами (запретами), а в EdgesT - истинными. Затем в циклах эти массивы используются для задания графа. При этом G[I] - это I-тый узел (начиная с единицы). Логический вывод Mind.set_graph(G) приводит к установлению двухстороннего движения по аксиоме симметричности (2) и запрету петель в узлах по антирефлексивности (1).

Теперь можно вывести информацию о наличии пути X.path(E, Y, loop, back) от узла X к узлу Y. В аргументах функции E - это ребро или массив типов рёбер по которым необходимо перемещаться по графу. Последние два параметра необязательны и по умолчанию имеют значение True. Если установить loop=False, то при поиске пути не будут учитываться петли в узле, а если back=False - перемещение между узлами будет происходить в одну сторону (что уместно для симметричных отношений, см. выше правый рисунок).

Функция path возвращает True, если существует путь и он проходит по истинным рёбрам. В противном случае, если пусть есть, но в нём присутствует хотя бы одно ложное ребро, функция вернёт False. Если же при данной информации нет пути по рёбрам с любым значением истинности (кроме Undef), то возвращается Undef: 

out "1-2:", (G[1]).path(@r, G[2], False, False)   //> 1-2: True   
out "1-4:", (G[1]).path(@r, G[4], False, False)   //> 1-4: True   
out "1-5:", (G[1]).path(@r, G[5], False, False)   //> 1-5: True   
out "1-8:", (G[1]).path(@r, G[8], False, False)   //> 1-8: True   
out "3-3:", (G[3]).path(@r, G[3], False, False)   //> 3-3: True   

out "1-7:", (G[1]).path(@r, G[7], False, False)   //> 1-7: False  
out "1-1:", (G[1]).path(@r, G[1], False, False)   //> 1-1: False  
out "7-7:", (G[7]).path(@r, G[7], False, False)   //> 7-7: False
out "8-8:", (G[8]).path(@r, G[8], False, False)   //> 8-8: False  

out "1-9:", (G[1]).path(@r, G[9], False, False)   //> 1-9: Undef  
out "9-9:", (G[9]).path(@r, G[9], False, False)   //> 9-9: Undef
Значение True для path 3-3 связано с наличием замкнутого цикла: 3-4-6-3. В тоже время path 1-1: False, так как такого цикла нет, хотя можно переместиться по 1-2-3-6-7-1, но два ребра в цикле ложные. Аналогично для 8-8.

Когда у графа заданы все рёбра @r (в True или False), то функция path всегда возвращает определённое значение. Если граф связный (по True-рёбрам @r), то это значение равно True. Для несвязных графов (распадающихся на подграфы не связанные True-рёбрами), получится True между узлами, принадлежащими одному подграфу и False между узлами различных подграфов.

Подчеркнём, что в не полностью определённом графе функция path позволяет выяснить только истинность отношения @p, но не его ложность. Когда есть не определённые рёбра, то в них может оказаться дорога, благодаря которой появится путь между узлами, который до этого по функции path считается равным False.

Полный код этого скрипта можно найти в файле cities1.ds.

Аксиомы для X @p Y

Задача становится интереснее, когда мы добавляем отношение X @p Y, истинное, если между узлами X и Y есть путь. В этом случае неполное описание графа может быть дано в терминах обоих отношений (из А в B есть дорога, но пути из A в C нет, и т.п.). Сформулируем свойства этого отношения.

Когда между X и Y есть ребро @r, то есть и путь @p. Это будет аксиомой (3). Несложно видеть, что отношение X @p Y, как и X @r Y, симметрично (4). Кроме этого, оно слабо транзитивно (5): 

Mind.add(
   (X @r Y) -> (X @p Y),                          // (3)  связь @r и @p
   (X @p Y) -> (Y @p X),                          // (4)  симметричность
   (X @p Z) & (Z @p Y) & X!=Y -> (X @p Y) )       // (5)  слабая транзитивность
Антирефлексивность !(X @p X) для отношения @p в общем случае не выполняется, так как на графе могут быть замкнутые пути (циклы).

Аксиома (5) означает, что если из X есть путь в Z и из Z есть путь в Y, то должен быть путь и из X в Y. В отличии от "обычной" транзитивности, в посылке добавлено условие X!=Y. Если бы его не было, то при X==Y, мы бы имели (X @p Z) & (Z @p X) -> (X @p X) или, в силу симметричности, (X @p Z) -> (X @p X). Это означает, что, если из X есть путь в некоторый узел Z, то есть и замкнутый пусть из X в X. Понятно, что в общем случае, это не верно.

Отметим также, что, в отличии от антисимметричных отношений, определение (3) не позволяет из симметричности @r вывести симметричность @p. Поэтому свойство симметричности должно указываться для обоих отношений.

Протестируем введенные в систему знания. Создадим при помощи конструктора GRAPH() пустой граф G и оператором nodes добавим в него 4 узла A,B,C,D: 

var G = GRAPH("G")                 // пустой граф
GRAPH = G                          // делаем его текущим
nodes $A, $B, $C, $D               // добавляем 4 узла

$A @r [$C,$D] = True               // задаём рёбра A-C, A-D
$A @p $B      = False              // нет пути A-B

Mind.verbose(1)                    // включена отладочная информация
Mind.set_graph(G)                  // запускаем логический вывод

Заданные рёбра соответствуют первому графу на рисунке ниже. Второй граф получился в процессе логического вывода: Mind.set_graph(G), где нарисованы только рёбра @r (сплошные линии). Справа приведен ещё один пример вывода:

Так была включён режим отладочной информации: Mind.verbose(1), на экране появится ход "рассуждений" объекта Mind для графа G: 
[1] ($A @r $A)? => False :  -> !($A @r $A)?
[1] ($B @r $B)? => False :  -> !($B @r $B)?
[4] ($B @p $A)? => False : !($A @p $B) -> !($B @p $A)?
[1] ($C @r $C)? => False :  -> !($C @r $C)?
[1] ($D @r $D)? => False :  -> !($D @r $D)?
[3] ($A @r $B)? => False : !($A @p $B) -> !($A @r $B)?
[2] ($C @r $A)? => True  :  ($A @r $C)  -> ($C @r $A)?
[3] ($A @p $C)? => True  :  ($A @r $C)  -> ($A @p $C)?
[4] ($C @p $A)? => True  :  ($A @p $C)  -> ($C @p $A)?
[5] ($B @p $C)? => False :  ($C @p $A)  ($B != $A) !($B @p $A) -> !($B @p $C)?
[2] ($D @r $A)? => True  :  ($A @r $D)  -> ($D @r $A)?
[3] ($A @p $D)? => True  :  ($A @r $D)  -> ($A @p $D)?
[4] ($D @p $A)? => True  :  ($A @p $D)  -> ($D @p $A)?
[5] ($B @p $D)? => False :  ($D @p $A)  ($B != $A) !($B @p $A) -> !($B @p $D)?
[5] ($C @p $B)? => False :  ($A @p $C)  ($A != $B) !($A @p $B) -> !($C @p $B)?
[5] ($D @p $B)? => False :  ($A @p $D)  ($A != $B) !($A @p $B) -> !($D @p $B)?
[5] ($D @p $C)? => True  :  ($D @p $A)  ($A @p $C)  ($D != $C)  -> ($D @p $C)?
[5] ($C @p $D)? => True  :  ($C @p $A)  ($A @p $D)  ($C != $D)  -> ($C @p $D)?
[2] ($B @r $A)? => False : !($A @r $B) -> !($B @r $A)?
[3] ($C @r $B)? => False : !($C @p $B) -> !($C @r $B)?
[3] ($D @r $B)? => False : !($D @p $B) -> !($D @r $B)?
[2] ($B @r $C)? => False : !($C @r $B) -> !($B @r $C)?
[2] ($B @r $D)? => False : !($D @r $B) -> !($B @r $D)?

Полный код этого скрипта можно найти в файле cities2.ds.

Изолированный и листовой узлы

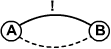К сожалению, заданные выше аксиомы не способны решить все возможные задачи. Например, они не справляются с третей и четвёртой задачей из начала документа. Проще всего это увидеть на простом графе из двух узлов, который приведен на рисунке справа. Очевидно, что он запрещён (дороги нет, а путь есть). Однако ни какой из введенных выше аксиом такая ситуация не противоречит.

В модели замкнутого мира, когда число узлов известно, можно добавить ещё аксиомы изолированного и листового узла.

Для этих двух случаев должны выполняться логические выводы, приведенные графически на рисунках ниже:

В первом случае делается вывод, что, если X изолирован, то из него не ведёт путь ни в какую вершину Y. Число ложных исходящих рёбер равно числу узлов графа n (одно из них - это петля, запрещённая антирефлексивностью). Во втором случае, если по единственно возможному пути из потенциального листа есть ребро @p, то должно быть и ребро @r

Для реализации этих аксиом определим двух демонов: 

def count(X, N):
   return X.count_out(@r, False) == X.graph().size() - N
   
def undef(X, Y) :
   return (X @r Y) == Undef

Демон count, при помощи метода .count_out узла X, вычисляет число исходящих из него рёбер @r (первый аргумент) с ложными значениями (второй аргумент) и сравнивает его с числом узлов графа, вычитая из него число N (для изолированного узла N=0, а для листа N=1). Так как аксиомы используются в различных методах, информации о текущем графе иногда нет, поэтому он запрашивается у узла X методом graph() и уже у него выясняется число узлов nodes().

Демон undef проверяет, что между узлами X и Y нет ребра @r. В аксиомах могут использоваться значения отношений типа X @r Y или сравнение узлов X!=Y. Более сложные сравнения и вычисления должны быть "упрятаны" внутрь демонов. Они используются в аксиомах только по значению, поставляя дополнительную информацию.

Теперь можно добавить аксиомы изолированного и листового узлов: 

Mind.add(
   count(X,0) -> !(X @p Y),                         // (6) изолированный никуда не ведёт
   count(X,1) & undef(X, Y) & (X @p Y) -> (X @r Y)) // (7) из листа есть одно ребро @r
Аксиома (6) в первой модели из начала раздела дополнительно позволяет установить, что замкнутого пути выходящего из узла B нет (это изолированный узел). Аксиома (7) позволила справиться с третей моделью, установив наличие дороги A-B (по-прежнему рисуем только рёбра @r):

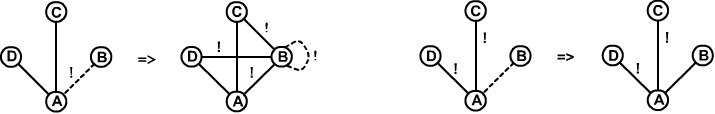
Как часто в логическом выводе используется та или иная аксиома (поле used), можно увидеть при выводе списка аксиом методом Mind.out(), вызванного после Mind.set_graph(G). Естественно, это также видно при включении режима Mind.verbose(1). Полный код этого примера находится в файле cities3.ds.

Транзитивное замыкание

Добавленные аксиомы, позволяют решать многие задачи. Однако,всё же не все. Например, для четвёртой задачи из начала раздела логический вывод по-прежнему не приводит к желаемому результату. Можно, конечно, добавлять ещё аксиомы, но проблема по-видимому связана с фундаментальными свойствами логики предикатов первого порядка. Существует теорема об ограниченности логики первого порядка, а именно: транзитивное замыкание нельзя выразить замкнутой формулой при помощи стандартных логических связок и кванторов.

Напомним понятие транзитивного замыкания. Пусть задано отношение не обладающее транзитивностью (выше это X @r Y). Всегда можно ввести отношение X @p Y, которое будет истинным всегда, когда истинно X @r Y и при этом обладать транзитивностью. Так, когда есть дорога X @r Y, то есть и путь X @p Y. Добавив дополнительно минимальное множество истинных рёбер X @p Y, всегда можно сделать отношение пути транзитивным.

В общем случае дополнить данное отношение рёбрами до транзитивного можно несколькими способами. Например, если граф состоит из двух несвязных подграфов, устанавливая @p в True между каждой парой узлов данного подграфа, мы получаем транзитивное замыкание. Однако рёбрами @p можно связать все узлы графа и это также будет транзитивное отношение. Однако, в отличии от транзитивного замыкания, оно не будет минимальным.

Для построения транзитивного замыкания существует простой алгоритм Уоршалла. Однако в виде замкнутой формулы его задать нельзя. В нашем случае ситуация осложняется трёхзначной логикой (рассуждения в условиях неполноты информации).

Заметим, что в последних двух аксиомах мы уже отошли от логики первого порядка, введя демона count. Так как нас интересует результат, получим его также не вполне аксиоматическими методами.

Корректность моделей

Объект Mind не только умеет подсчитывать разрешённые модели (.count_models), но их порождать их явным образом. В этих моделях все рёбра @r определены (заданы в значение True или False). Поэтому, при помощи функции .path можно проверить соответствие отношений @r и полученных при логическом выводе отношений @p. Те, которые не выдержали проверки, необходимо отбросить. Если во всех оставшихся моделях некоторое ребро (@r или @p) всегда принимает одно и тоже значение, значит это и есть "решение задачи". Если же в одних моделях ребро равно True, а в других - False, значит исходная информация слишком неполна и соответствующее отношение следует считать Undef.

Рассмотрим реализацию этого метода. Введём демона, который проверяет валидность полностью определённой модели (в которой заданы все рёбра @r): 

def correct(G) 
{
   for I in range(1, G.size()+1) :
      for J in range(I, G.size()+1) {  
         var V = G[I].path(@r, G[J], False, False)
         if (G[I] @p G[J]) == Undef & V != Undef {// аксиома не задала путь @p
            G[I] @p G[J]  = V                     // path умнее аксиом - меняем граф
            continue                              // и продолжаем
         }
         if V != (G[I] @p G[J]) :                 // явное задание @p противоречит path
            return False                          // значит эта модель невалидна
      }
   return True                                    // всё нормально
}
В демоне происходит поиск пути по рёбрам @r между каждой парой узлов G[I] и G[J]. Если результат path не совпадает с определённым (например, условиями задачи) значением отношения @p, модель считается неверной. Этого демона передадим методу validator объекта Mind перед вызовом генератора моделей .get_models. Теперь все сгенерённые модели с полностью определёнными рёбрами @r будут проверяться на самосогласованность: 
Mind.validator(correct(G))
var Models = Mind.get_models(G, @r, 0)           // 0 означает, что нет ограничения по числу моделей
out "num models: ", Models.size()
Для четвёртой задачи будет получено 4 модели, так как исходная информация не фиксирует значения рёбер A-C и D-B. Теперь можно вызвать функцию value, которая определит значение ребра A @r B. Если во всех моделях его значение одно и тоже, то оно и будет возвращено функцией. Иначе, получится Undef: 
out "$A @r $B = ", Mind.value(Models, $A @r $B)
Это даёт True, что и ожидается для данных начальных условий. Заметим, что при таком подходе достаточно использовать только базовые аксиомы (без аксиом изолированного и листового узла).

Полный код этого примера находится в файле cities4.ds.

Аксиома с алгоритмом

Рассмотренный выше метод оценки по моделям универсален и может применяться в различных приложениях. Однако, для задачи с городами возможно ещё одно решение, которое для больших графов оказывается более эффективным. В нём используется аксиома с демоном, внутри которого реализован достаточно сложный алгоритм. Но сначала приведём соответствующий список аксиом: 

Mind.add(
  !(X @r X),                                      // (1) антирефлексивность
   (X @r Y) -> (Y @r X),                          // (2) симметричность
   
   (X @r Y) -> (X @p Y),                          // (3) связь @r и @p
   (X @p Y) -> (Y @p X),                          // (4) симметричность
   (X @p Z) & (Z @p Y) & X!=Y -> (X @p Y),        // (5) слабая транзитивность
   
  !alternative(X,Y) & (X @p Y) -> (X @r Y))       // (6) нет альтернативного пути
Как видно, к базовым аксиомам добавлена аксиома (6), устанавливающая ребро @r в True, если от X к Y идёт путь @p и нет потенциальных альтернативных путей между этими узлами. Такой путь следует понимать как потенциальную возможность непрямого пути между двумя узлами. Поясним это на примерах:

На первых трёх картинках приведены графы из трёх узлов, для которых известно, что путь @p из A в B есть, но неизвестно есть ли прямая дорога @r. В первом случае она может отсутствовать так как есть явный путь A-C-B. Во втором случае ребро A @r B также может быть ложным, так как рёбра A @r C и C @r B неопределены, а, следовательно, в них может оказаться дорога. Поэтому в этих двух случаях следует считать A @r B неопределённым (есть потенциальный альтернативный путь). В третьем примере есть явный запрет для альтернативного пути A-C-B, поэтому следует сделать логический вывод, что дорога A-B есть.

Ещё одна аксиома в форме !alternative(X,Y) & !(X @r Y) -> !(X @p Y) делает аналогичный вывод: если ребро @r запрещено и нет альтернативных путей, то и пути @p нет. Но дополнительно задавать её не нужно, так как в конъюнктивной нормальной форме она совпадает с (6).

Поиск альтернативного пути

Напишем теперь демона, который реализует алгоритм поиска потенциального альтернативного пути (этого демона надо объявить выше вызова Mind.add) По определению, альтернативный путь от узла X к узлу Y проходит через один и более узлов (т.е. это непрямой путь X-Y). При этом он должен проходить, либо по истинным True-рёбрам @r, либо между узлами, которые не связанны рёбрами @r, т.е. по @r-"рёбрам", имеющим значение Undef. Так как связи нет (она не известна) такой путь потенциально может появиться, оказавшись альтернативным путём. 

def alternative(X,Y)
{
   if X == Y : return False
   var Open  = []                                 // очередь узлов из которых ищем путь
   var Close = []                                 // список узлов в которых уже были
   Open.push(X)                                   // помещаем в Open стартовый узел X
   Close.push(X)
   while !Open.empty()                            // пока очередь Open не пустая
   {
      var P = Open.pop()                          // извлекаем узел из конца очереди
      for Q in !(X==P & Q==Y) & (P @r Q) != False & (X @p Q) != False {
         if Q == Y:                               // если это Y, то 
            return True                           // путь найден 
      
         if Close.find(Q) < 0 {                   // ещё в Q не были
            Open.push(Q)                          // помещаем для дальнейшего поиска
            Close.push(Q)                         // запоминаем, что в нём были
         }
      }
   }
   return False
}

Алгоритм alternative реализует поиск в глубину. Для этого вводится две очереди. Очередь Open содержит узлы подлежащие дальнейшему анализу и Close - узлы, где мы уже были. Очередной узел P извлечённый из Open порождает следующих кандидатов Q куда из P можно перейти. При этом эти кандидаты должны удовлетворять определению альтернативного пути: он не должен быт прямым !(X==P & Q==Y) и должен проходить по неопределённым Undef или истинным True рёбрам (P @r Q) != False. Кроме этого, если из X есть явный запрет пути в Q (он может присутствовать в условиях задачи), то этот путь также не является альтернативным: (X @p Q) != False.