Алгебра логики
Основные связки
В двоичной логике каждому утверждению приписывается одно из двух значений: истина (\(\T\)) или ложь (\(\F\)). Константное утверждение (\(A\) : "сейчас идет дождь") называется высказыванием. Утверждение может зависеть от переменных \(P(x):~ x>0\). Такие переменные утверждения (\(=\) предикаты) истинны при одних \(x\) и ложны при других.
Это очень ограниченная модель "человеческой логики". Высказывание "сейчас идёт дождь" истинно или ложно, и третьего не дано. Хотя для многих "одна дождинка — ещё не дождь". Тем не менее, в формальных теориях, таких как математика, двоичной логики вполне достаточно.
Простые утверждения (высказывания, предикаты) объединяют в более сложные при помощи логических связок (=операций) \(\neg\), \(\&\),\(\vee\), \(\equiv\). Эти связки являются функциями, аргументы и значения которых принадлежат множеству \(\{\T,\F\}.\)
Логическое "ИЛИ" \(A\vee B\) истинно, если истинно или \(A\) или \(B\) или оба (хотя бы одно). Представим это утверждение при помощи таблицы истинности, где в колонках \(A\) и \(B\) перечисленны все варианты значений истинности высказываний \(A\) и \(B\), а под символом \(\vee\) находится результат логической операции \(A\vee B\) (она называется также дизъюнкцией):
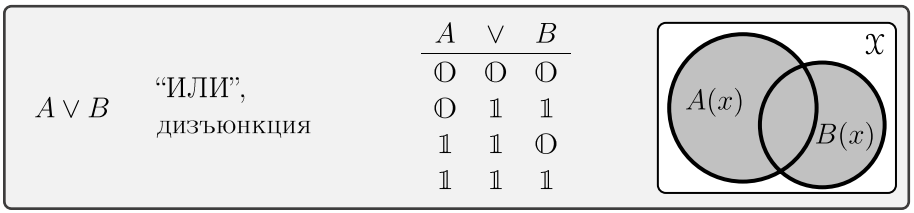
Так \(\F\vee \F\) — это \(\F\), а \(\F \vee \T\) — это \(\T\). Справа кругами изображены области истинности предикатов \(A(x)\) и \(B(x)\) на плоскости всех значений \(x\in\mathbb X\). Заштрихованная область — это результирующий предикат \(A(x)\vee B(x)\).
Логическое "И" или конъюнкция истинно, только если истинны оба высказывания:
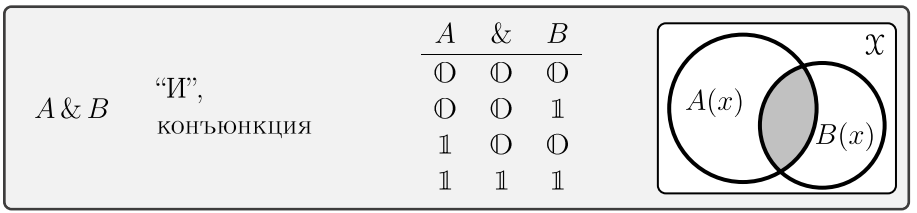
Предикат конъюнкции \(A(x)\,\&\,B(x)\) истинен в области пересечения множеств истинности \(A(x)\) и \(B(x)\).
Операция логического отрицания меняет истину на ложь и наоборот, т.е. \(\neg \T \) это \(\F\), а \(\neg \F \) — это \(\T\). Кроме символа \(\neg\), используется также черта сверху (\(\bar{A}\) — тоже, что и \(\neg A\)):

Если два логических выражения имеют одинаковые значения истинности или лжи, то говорят, что они эквивалентны. Этот факт выражается ещё одной логической связкой:
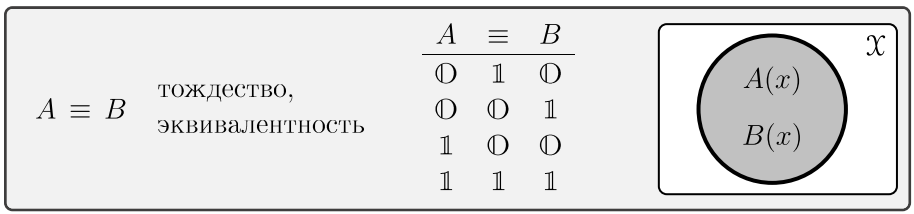
Эквивалентность \(A\equiv B\) похожа на равенство \(x=y\), однако мы будем их различать. Например, в арифметике \((x=y) ~\equiv~ (y=x)\), где \(x,y\in\mathbb{N}\), а \(x=y\) — это предикат равенства (истинный или ложный). Для логических формул \(P,Q\) будет использоваться запись \(P=Q\), когда формулы полностью совпадают.
Логическая функция двух аргументов определяется последовательностью из \(4=2^2\) символов \(\T\) или \(\F\). Для логического ИЛИ эта последовательность имеет вид \(\F\T\T\T\), а для эквивалентности \(\T\F\F\T\). Возможно \(16=2^4\) подобных последовательностей (двоичных чисел с 4-мя разрядами). Как мы увидим дальше, любую логическую функцию можно выразить через связки \(\&,\vee,\neg\).
Исключающее ИЛИ
В качестве примера рассмотрим разделительное "ИЛИ" \(A\oplus B\): "она любит или Колю или Васю" (но не обоих). Оно отлично от объединяющего "ИЛИ" \(A\,\vee\,B\), которое истинно и когда истинны оба высказывания. Разделительное "ИЛИ" описывается следующей таблицей истинности и двумя эквивалентными логическими выражениями:
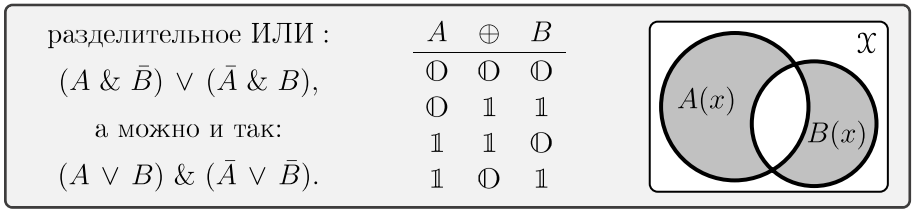
Так, подстановка последней строки в таблице истинности во вторую формулу даёт: \[(\T\vee \T)\,\&\,(\bar{\T}\vee\bar{\T})\equiv \T\,\&\,(\F\vee\F)\equiv\T\,\&\,\F \equiv \F.\] Отметим, что: \[ A\vee B \equiv A\oplus B\oplus (A\,\&\, B),~~~~~ \neg A \equiv A\oplus \T, \] т.е. все связки выражаются через \(\oplus\), \(\&\) и \(\T\) (т.н. полиномы Жегалкина).
Дерево формулы
Любую логическую формулу (=выражение) можно представить в виде дерева, задающего последовательность вычислений:
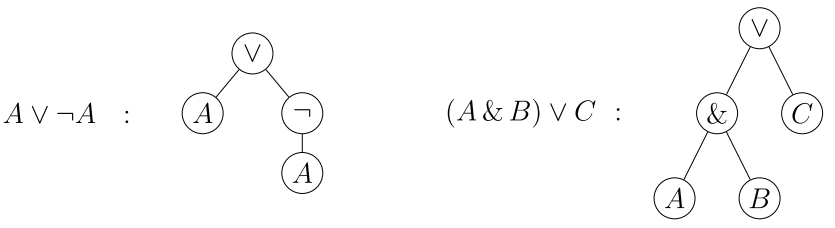
В вершине дерева стоит последняя вычисляющаяся функция, а внизу, на "листьях" — высказывания. Вычисление выражения идёт снизу-вверх. Если на "листьях" стоят одни и те-же высказывания их можно объединить, получив ориентированный ациклический граф.
Введём соглашение о приоритетах логических функций: самый высокий приоритет у отрицания "\(\neg\)", чуть ниже у "\(\&\)" и ещё ниже у "\(\vee\)"; самый низкий приоритет у эквивалентности "\(\equiv\)". Если на приоритеты не полагаются, то используют скобки. Например, формула \(A\,\&\, B \vee \neg C \, \& \, D\) — это тоже, что и \((A\,\&\, B ) \vee ((\neg C) \, \& \, D),\) а формула \(A\vee B\equiv C\,\&\,D\) — это \((A\vee B)\equiv(C\,\&\,D)\).
Тавтологии
Логическое выражение, истинное при любых значениях входящих в него высказываний, называется общезначимым или тавтологией. Докажем, например, общезначимость следующей формулы: \[ A \,\&\, (A\vee B) ~ \equiv~ A . \] Для этого запишем её таблицу истинности. Высказывания принимают значение \(\F\) и \(\T\). Если \(A\equiv \F\), то \(B\) может быть равно \(\F\) или \(\T\). Аналогично для \(A\equiv \T\). Это даёт четыре варианта, которые подпишем под высказываниями, входящими в формулу. Затем под каждой логической связкой (сначала \(\vee\), затем \(\&\) ) будем подписывать её результат: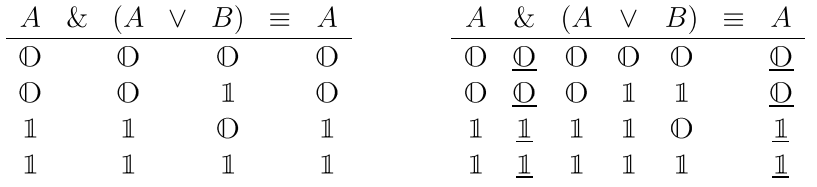
Осталось сравнить подчёркнутые значения. Так как они совпадают, в колонке \(\equiv\) везде необходимо поставить \(\T\), т.е. это тавтология.
В качестве простого упражнения предлагается доказать, что формула \(A\vee \neg A\) также является тавтологией. Она имеет смысл закона исключения третьего ("или \(A\) или не \(A\)"). На месте \(A\) может стоять как константное высказывание "сейчас идет дождь", так и предикат. Например: \((x=y)\,\vee\,\neg (x=y)\), т.е. \(x\) или равно или не равно \(y\).
Булева алгебра
Существует множество формул, имеющих одинаковые таблицы истинности. Соединение их символом эквивалентности "\(\equiv\)" приводит к тавтологиям. Часть из них составляет булеву алгебру.
Так, логические "И", "ИЛИ" — симметричны и ассоциативны: \[ \begin{array}{llcllcll} ~ &A\, \&\,B & ~\equiv~ & B \,\&\, A , & ~~~~& A \,\&\,(B \,\&\, C) & ~\equiv~ & (A \,\&\, B) \,\&\, C , \\[2mm] &A \vee B & ~\equiv~ & B \vee A , &~~~~~& A \vee (B \vee C) & ~\equiv~ & (A \vee B) \vee C. \end{array} \] Для них выполняются законы дистрибутивности: \[ \begin{array}{llcl} ~~~~~~~~~~~~~~ &A \, \& \, (B \vee C) & ~\equiv~ & (A \,\&\, B)\, \vee \, (A \,\&\, C), \\[2mm] &A \vee (B \,\&\, C) & ~\equiv~ & (A \vee B) ~\&~ (A \vee C) \end{array} \] и более специфические свойства поглощения: \[ \begin{array}{llcllcll} ~~~~~~~~~~ &A \,\&\, A & ~\equiv~ & A , & ~~~~~~~~~~~~& A\,\&\,(A\vee B) & ~\equiv~ & A , \\[2mm] &A \vee A & ~\equiv~ & A , & ~~~~~~~~~~~~& A\vee(A\,\&\,B) & ~\equiv~ & A. \end{array} \] Справедлив закон двойного отрицания и правила де-Моргана: \[ \begin{array}{llcllcll} &\neg(\neg A) & ~\equiv~ & A ,&~~~~~~~~& \neg(A \,\&\, B) &~\equiv~ & \neg A \vee \neg B ,\\[2mm] & & & &~~~~~~~~& \neg(A \vee B) & ~\equiv~ & \neg A \,\&\, \neg B. \end{array} \] В алгебру можно ввести константы: "\(\T\)" (истина), "\(\F\)" (ложь) и записать закон исключения третьего в двух формах: \[ ~~~~~~~~~~~~~~~A\,\&\, \neg A ~\equiv~ \F,~~~~~~~~~~~~~~~~~~~~~~ A \vee \neg A ~\equiv~ \T, \] а также следующие очевидные соотношения: \[ ~~~A\,\&\, \F ~\equiv~ \F,~~~~~~~ A\,\&\,\T ~\equiv~ A,~~~~~~~~ A \vee \T ~\equiv~ \T,~~~~~~~ A \vee \F ~\equiv~ A. \] Стоит обратить внимание на симметричность всех формул относительно перестановки \(\&\) и \(\vee\), с одновременной заменой \(\F\) на \(\T\) и наоборот.
\(\diamond\) Проведём при помощи этих тождеств упрощение следующего логического выражения: \[ A ~ \& ~ (\bar{A}\,\vee\,B) ~\equiv~ (A\,\&\, \bar{A})\,\vee\,(A\,\&\, B) ~\equiv~ \F\,\vee\,(A\,\&\, B) ~\equiv~ A ~\&~ B, \] где сначала использовано свойство дистрибутивности конъюнкции (\(\&\)), затем закон исключения третьего и тождество \(\F\vee A\equiv A\). Непрерывная цепочка эквивалентностей основана на свойстве транзитивности: если \(A\equiv B\) и \(B\equiv C\), то \(A\equiv C\), что записывается как \(A\equiv B \equiv C\). Аналогично стоит доказать, что \(A \, \vee \, (\bar{A}~\&~B) ~~\equiv~ A \,\vee\, B\). \(\square\)