Множества
Определения
Размышления о совокупностях объектов создало математику и стало её основой. Множество — это фундаментальное понятие, обобщающее интуитивное представление об объединении объектов по некоторому признаку. Множества состоят из элементов. Все элементы данного множества различны и порядок их перечисления не важен.
\(\diamond\) Примеры: множество целых чисел, множество прямых, множество симпатичных девушек, множество этих трёх множеств. \(\square\)
Множество определено, когда задан способ, позволяющий выяснить содержит ли оно данный элемент. Если элемент \(a\) принадлежит множеству \(\mathbb A\) (содержится в нём), то это обозначается следующим образом: \(a\in \mathbb A\) (предикат с двумя аргументами \(a\), \(\mathbb A\), который истинен, если \(a\) принадлежит \(\mathbb A\) и ложен, в противном случае). Если элемент \(a\) не принадлежит множеству \(\mathbb A\), то это обозначается так: \(a\not\in \mathbb A\) или \(\neg(a\in\mathbb A)\). Два множества \(\mathbb A\) и \(\mathbb B\), состоящие из одних и тех же элементов, равны: \(\mathbb A= \mathbb B\) (предикат равенства).
Конечные множества можно описать, перечислив их элементы. В общем случае множество задаётся при помощи условия: \(\mathbb A =\{x|~условие\}\):
\(\diamond\)
\(\mathbb A=\{3,2,1,5,4\}\)
— множество натуральных чисел \(\mathbb N\) от 1 до 5.
\(\diamond\) \( \mathbb A=\{x|x\in \mathbb N,~0 < x < 6\}\)
— это снова натуральные числа от 1 до 5. \(\square\)
Если каждый \(a\in\mathbb A\) (принадлежащий множеству \(\mathbb A\)) также \(a\in\mathbb B\) (принадлежит и множеству \(\mathbb B\)), то говорят, что \(\mathbb A\) является подмножеством (частью) множества \(\mathbb B\). Для выражения этого вводится третий предикат: \(\mathbb A\subseteq \mathbb B\) со свойствами:
 \[
\begin{array}{lcllll}
\mathbb A\subseteq \mathbb A,~~~само~себе~подмножество,\\[2mm]
Если (\mathbb A\subseteq \mathbb B)\,\&\,(\mathbb B\subseteq \mathbb A)
~то~\mathbb A= \mathbb B,\\[2mm]
Если (\mathbb A\subseteq \mathbb B)\,\&\,(\mathbb B\subseteq \mathbb C)
~\,то~\mathbb A\subseteq \mathbb C
.
\end{array}
\]
\[
\begin{array}{lcllll}
\mathbb A\subseteq \mathbb A,~~~само~себе~подмножество,\\[2mm]
Если (\mathbb A\subseteq \mathbb B)\,\&\,(\mathbb B\subseteq \mathbb A)
~то~\mathbb A= \mathbb B,\\[2mm]
Если (\mathbb A\subseteq \mathbb B)\,\&\,(\mathbb B\subseteq \mathbb C)
~\,то~\mathbb A\subseteq \mathbb C
.
\end{array}
\]
Элементами множества могут выступать другие множества. Для избежания противоречий считают, что множество не может быть своим элементом: \(\mathbb A \not\in \mathbb A\).
\(\diamond\) Элементами множества \(\mathbb{Z}=\{\,\{a,b\},~\{a\}\,\}\) выступают два множества \(\mathbb{X}=\{a,b\}\) и \(\mathbb{Y}=\{a\}\). \(\square\)
где \(\{\{a\}\}\) — множество из одного элемента \(\{a\}\), который есть множество с элементом \(a\).
Множество \(\varnothing=\{\}\), не содержащее элементов, называется пустым. Пустое множество является подмножеством любого множества: \(\varnothing \subseteq \mathbb{A}\). У множества \(\mathbb{A}\) с \(n\) элементами \(2^n\) подмножеств включая \(\mathbb{A}\) и \(\varnothing\).
Операции с множествами
Для образования новых множеств вводится три функции (операции), ставящие в соответствие двум множествам, третье: \[ \begin{array}{llll} &объединение: & \mathbb A\cup \mathbb B ~~= & \{ x | ~~ (x\in \mathbb A) \,\vee\, (x\in \mathbb B)\}, \\ &пересечение: & \mathbb A\cap \mathbb B ~~= & \{ x | ~~ (x\in \mathbb A) ~\&~ (x\in \mathbb B)\}, \\ &дополнение: & \mathbb A - \mathbb B ~~= & \{ x | ~~ (x\in \mathbb A)~\&~ (x\not\in \mathbb B)\}, \\ &симметричная~разность: & \mathbb A \,\Delta\, \mathbb B ~~= & (\mathbb{A}-\mathbb{B})\cup(\mathbb{B}-\mathbb{A}). \end{array} \]
В объединённое множество попадают все элементы из обоих множеств. В пересечение — только общие для множеств элементы, а в дополнение \(\mathbb A - \mathbb B\) только те элементы \(\mathbb A\), которые не принадлежат \(\mathbb B\). Эти базовые функции наглядно представляются при помощи диаграмм Эйлера-Венна, в которых замкнутая область обозначает некоторое множество. Область геометрического пересечения двух множеств будет множественным пересечением \(\mathbb A\cap \mathbb B\) (она закрашена), и т.д.:
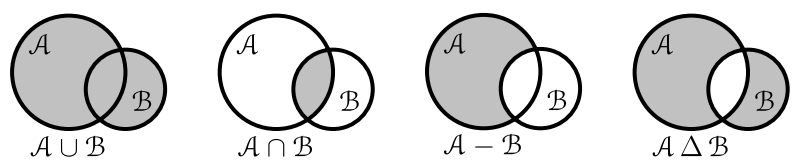
Ясно, что \(\mathbb{A}\cup\mathbb{A}=\mathbb{A}\), \(\mathbb{A}\cap\mathbb{A}=\mathbb{A}\) и если \(\mathbb{A}\subseteq\mathbb{B}\), то \(\mathbb{A}\cap\mathbb{B}=\mathbb{A}\). Результатом действия функций может быть пустое множество. Например: \((\mathbb A- \mathbb B)\cap \mathbb B = \varnothing\). Отметим мнемонику: значок \(\cup\) — это чашка в которую "сливаются" (объединяясь) оба множества.
При помощи диаграмм Эйлера-Венна, несложно мотивировать различные тождества для введенных операций. Например, в качестве простого упражнения, предлагается проверить свойства коммутативности и ассоциативности для объединения множеств: \[ \mathbb{A}\cup\mathbb{B}=\mathbb{B}\cup\mathbb{A},~~~~~~~~~~~~~(\mathbb{A}\cup\mathbb{B})\cup\mathbb{C}=\mathbb{A}\cup(\mathbb{B}\cup\mathbb{C}). \] и такое же для пересечения \(\cap\). Затем доказать их дистрибутивность, которая также верна, если заменить \(\cup\) на \(\cap\) и наоборот (поменять объединение и пересечение местами): \[ (\mathbb{A}\cup\mathbb{B})\cap\mathbb{C} = (\mathbb{A}\cap\mathbb{C})\cup(\mathbb{B}\cap\mathbb{C}). \] Ещё два тождества с операцией дополнения: \[ \mathbb{A}\cap (\mathbb{B}-\mathbb{C}) = (\mathbb{A}\cap\mathbb{B}) - (\mathbb{A}\cap\mathbb{C}), \] \[ (\mathbb{A}-\mathbb{B})\cup(\mathbb{B}-\mathbb{A}) = (\mathbb{A}\cup \mathbb{B}) - (\mathbb{A}\cap \mathbb{B}) \] также несложно доказать, пользуясь этими диаграммами.
Предикаты
 При помощи теории множеств можно определять предикаты.
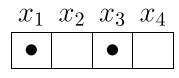
Например, на множестве \(\mathbb X=\{x_1,x_2,x_3,x_4\}\)
из четырёх элементов, зададим предикат \(A(x)\)
с одним аргументом.
Пусть \(A(x_1)=\T\), \(A(x_2)=\F\), \(A(x_3)=\T\), \(A(x_4)=\F\), где \(\T\) — это истина, а \(\F\) — ложь.
Эквивалентно, его можно считать равным
подмножеству элементов \(\mathbb A \subseteq \mathbb X\), для которых \(A(x)\) истинно:
При помощи теории множеств можно определять предикаты.
Например, на множестве \(\mathbb X=\{x_1,x_2,x_3,x_4\}\)
из четырёх элементов, зададим предикат \(A(x)\)
с одним аргументом.
Пусть \(A(x_1)=\T\), \(A(x_2)=\F\), \(A(x_3)=\T\), \(A(x_4)=\F\), где \(\T\) — это истина, а \(\F\) — ложь.
Эквивалентно, его можно считать равным
подмножеству элементов \(\mathbb A \subseteq \mathbb X\), для которых \(A(x)\) истинно:
\[ \mathbb A = \{x_1, x_3\} \]
Определим теперь предикат \(B(x,y)\) с первым аргументом из множества \(\mathbb X = \{x_1,x_2,x_3\}\),
а со вторым — из множества \(\mathbb Y = \{y_1,y_2,y_3,y_4,y_5,y_6\}\).
Они могут иметь разный смысл (\(\mathbb X\) — это точки, \(\mathbb Y\) — прямые),
или одинаковый (и \({\mathbb X}\), и \({\mathbb Y}\)
— натуральные числа).
Составим множество всех упорядоченных пар которое называют прямым произведением:
\[
\mathbb X \times \mathbb Y = \{(x_1,y_1),...,(x_1,y_6),\,(x_2,y_1),...,(x_2,y_6),\,(x_3,y_6),...,(x_3,y_6)\}.
\]
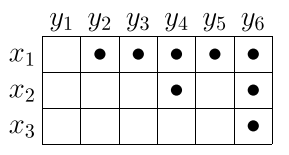 Предикат зададим подмножеством \(\mathbb B\subseteq\mathbb X \times \mathbb Y\)
на котором он истинный:
\[
\begin{array}{ll}
\mathbb B:\{
&(x_1,y_2),(x_1,y_3),(x_1,y_4),(x_1,y_5),(x_1,y_6),\\
&(x_2,y_4),(x_2,y_6),\\
&(x_3,y_6)~\}\\
\end{array}
\]
Предикат зададим подмножеством \(\mathbb B\subseteq\mathbb X \times \mathbb Y\)
на котором он истинный:
\[
\begin{array}{ll}
\mathbb B:\{
&(x_1,y_2),(x_1,y_3),(x_1,y_4),(x_1,y_5),(x_1,y_6),\\
&(x_2,y_4),(x_2,y_6),\\
&(x_3,y_6)~\}\\
\end{array}
\]
Таблица соответствует всем \(18=3\cdot 6\) упорядоченным парами 8 точек стоит там, где \(B(x,y)\) истинен. Предикат \(B(x,y)\) может обозначать "число \(x\) — собственный делитель \(y\)" (\(x\neq y\) ), если \(\mathbb X=\{1,2,3\}\), а \(\mathbb Y=\{1,...,6\}\). Например \(B(2,4)\) истинно, а \(B(3,4)\) — ложно.
Точно также определяются предикаты с тремя аргументами (между тремя объектами): \(C(x,y,z):~ \mathbb{C}\subseteq \mathbb{X}\times\mathbb{Y}\times\mathbb{Z}\) и т.д.
Функции
Если бинарный (с двумя аргументами) предикат \(F(x,y)\)
для каждого \(x\in\mathbb X\) истинен для не более одного \(y\in \mathbb Y\),
его называют функциональным. Он определяет функцию \(y=f(x)\), которая элементу
\(x\) ставит в соответствие единственный элемент \(y\):
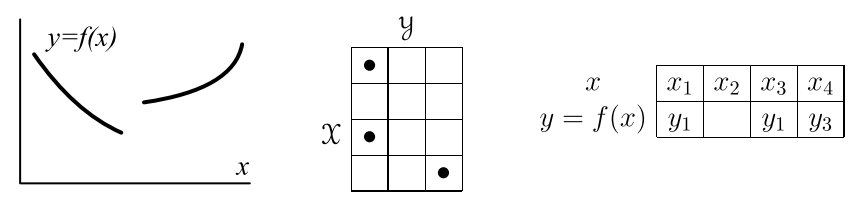
Значения \(x\) для которых определено отношение (непустые строки) называется областью определения функции. Если в таблице предиката есть пустые строчки, то это частично определённая (не при всех значениях \(x\)) функция. Аналогично, предикат \(F(x,y,z)\) может определять функцию \(z=f(x,y)\) и т.д.
Бесконечные множества
Конечные множества (имеющие конечное число элементов) являются очень конструктивными математическими объектами. Их можно (по крайней мере в принципе) "изобразить" на бумаге или в памяти компьютера. Иначе обстоит дело с бесконечными множествами. Например, не существует "самого большого" натурального числа и множество \(\mathbb N = \{0,1,2,...\}\) бесконечно.
Различают потенциальную и актуальную бесконечности. Первая подразумевает, что конкретное число \(x\in\mathbb N\) может быть сколь угодно большим. Актуальная бесконечность представляет совокупность всех натуральных чисел или всех точек отрезка \([0...1]\), как самостоятельный математический объект (законченную совокупность). С актуальными бесконечностями связаны определённые проблемы, однако сейчас мы их обсуждать не будем, а введём понятие счётного множества. Множество называется счётным, если все его элементы можно пронумеровать, т.е. каждому элементу поставить в соответствие уникальное натуральное число.
\(\diamond\) Любое подмножество натуральных чисел \(\mathbb N = \{0,1,2,...\}\) счётно. Например, упорядоченные по возрастанию чётные числа можно пронумеровать, перечислив их как \(\{0,2,4,...\}\) или при помощи функции соответствия \(f(n)=2n\) такой, что \(f(0)=0\), \(f(1)=2\), \(f(2)=4\),....
\(\diamond\) Счётны целые числа, которых кажется "больше", чем натуральных. Их перечисление такое: \(\{0,-1,1,-2,2,-3,3,...\}\) или при помощи функции \(f(n)\), равной \(n/2\) при чётных \(n\) и \(-(n+1)/2\) — при нечётных.
\(\diamond\) Множество рациональных чисел \(\mathbb Q\) — это все несократимые дроби \(p/q\), где \(p,q \in \mathbb N\) и \(q\neq 0\). Каждому числу \(p/q\) можно присвоить уникальный номер \(n=2^p\cdot 3^q\), поэтому множество \(\mathbb Q\) счётно. Так как любое число единственным образом раскладывается на множители, то по данному \(n\) можно получить \(p\), \(q\) и наоборот. Заметим, что рациональные числа (как и целые) нельзя перечислить по возрастанию и введенная нумерация даёт последовательность \(\{0,\,1,\,2,\,1/2,\,3,\,4,\,1/3,\,3/2,\,...\}\).
\(\diamond\) Счётно множество всех строк конечной длины, состоящих из букв конечного алфавита. Такие строки можно упорядочить сначала по длине (строки из одного символа, строки из двух символов и т.д.), а строки одинаковой длины отсортировать по алфавиту ( лексографический порядок). Каждая строка в таком списке имеет свой порядковый номер.
\(\diamond\) Любые определения, формулы, доказательства и алгоритмы счётны, т.к. являются конечными строками из букв конечного алфавита. \(\square\)