Силлогизмы
Сократ и блондинки
Кванторы в логике очень древнее изобретение. Достаточно вспомнить аристотелевское:
Все люди бессмертны. Сократ — человек.Введем предметное множество различных существ и предметную константу "\(s\)" для идентификации Сократа. Потребуется также два предиката \(M(x)\): "\(x\) является человеком" и \(I(x)\): "\(x\) — бессмертен". Тогда в рамках формальной теории этот силлогизм (логическое следствие) можно записать так: \[ \forall_x\, \bigl(M(x)\to I(x)\bigr),~~~~~M(s)~~~~~~~~\Rightarrow~~~~~~~~I(s). \] Из двух посылок (логических утверждений) вводится третья. В такой формальной записи содержательный смысл предикатов не играет роли и этот вывод общезначим (справедлив в любой теории).
Следовательно, Сократ бессмертен.
Приведём ещё один пример силлогизма:
Всякая блондинка умна. Мэри не умна.Введём предикаты \(B(x)\): "\(x\) — блондинка" и \(W(x)\): "\(x\) — умна", а также константу \(m\) для обозначения бедной Мэри. Формализация рассуждения тогда будет иметь следующую запись: \[ \forall_x ( B(x)\to W(x)),~~~~~\neg W(m)~~~~~~\Rightarrow~~~~~~\neg B(m). \] Оба вывода обосновываются следующим образом. Квантор всеобщности говорит о всех сущностях и, в частности, о Сократе или Мэри. Поэтому, по правилу \(({\bf Ex})\), его можно опустить, заменив \(x\) на константу: \(\forall_x\,A(x)\Rightarrow A(a)\). В результате получатся обычные формулы из алгебры высказываний, например, \(B(m)\to W(m)\). Соответствующие заключения теперь не сложно сделать по резолюции: \[ \neg B(m)\vee \underline{W(m)},~~~\neg \underline{W(m)}~~~~~\Rightarrow~~~~~\neg B(m). \]
Следовательно, Мэри не является блондинкой.
Важно понимать, что истинность или ложность каждой посылки в силлогизме может быть различной в различных интерпретациях. Понятно, что существует мир (к сожалению, по-видимому наш), в котором утверждение \(\forall_x\, \bigl(M(x)\to I(x)\bigr)\) ложно, в прочем, к счастью, также как и утверждение \(\forall_x\, ( B(x)\to W(x))\). Однако, если посылки истинны, то и следствие будет обязательно истинным. Поэтому из исходных истинных утверждений (аксиом) всегда будут следовать истинные результаты (теоремы).
Типы утверждений по Аристотелю
Аристотель выделял четыре типа утверждений \({\bf A}\), \({\bf E}\), \({\bf O}\), \({\bf I}\) о двух предикатах \(P(x)\), \(Q(x)\): \[ \begin{array}{cllll} {\bf A}(P,Q) &: &все~P~ есть~Q & ~: & \forall_x\, [P(x)\to \phantom{\neg}Q(x)],\\ {\bf E}(P,Q) &: &все~P~ не~Q & ~: & \forall_x\, [P(x)\to \neg Q(x)] \end{array} \] Примеры: "все квадраты — прямоугольники", "все млекопитающие — живородящие"; "нет ни одного летающего крокодила", "нет круглых квадратов" (любой \(x\), если он квадрат, то он не круглый). В этих утверждениях важна импликация. Так, мы не говорим "любой является квадратом и прямоугольником", а именно "любой, если он квадрат, то он будет прямоугольником". К тому же \(\forall_x\,[P(x)\,\&\,Q(x)]\) эквивалентно двум утверждениям \(\forall_x\,P(x)\) и \(\forall_x\,Q(x)\), которые обычно ложны. \[ \begin{array}{cllll} {\bf O}(P,Q) &: &некоторые ~P~ не~ Q & : & \exists_x\, [P(x)\,\&\, \neg Q(x)],\\ {\bf I}(P,Q) &: &некоторые~P~есть~Q & : & \exists_x\, [P(x)\,\&\, \phantom{\neg} Q(x)]. \end{array} \] Примеры: "некоторые блондинки умны", "некоторые эллипсы — это окружности", "некоторые грибы не съедобны". В данных случах не уместна импликация. Мы не скажем "нечто является эллипсом, следовательно это окружность", а именно "бывает нечто являющееся и эллипсом и окружностью". Заметим, что \(\neg {\bf O} ~\equiv~ {\bf A}\), а \(\neg {\bf I} ~\equiv~ {\bf E}\).
Диаграммы Эйлера-Венна
Утверждения \({\bf A}\), \({\bf E}\), \({\bf O}\), \({\bf I}\) можно представить, как и множества, при помощи диаграмм Эйлера-Венна на плоскости возможных значений \(x\):
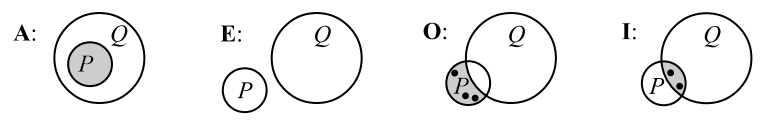
Два утверждения относительно трёх свойств могут логически влечь третье утверждение:
\[{\bf A}(P,Q), {\bf A}(Q,S) \Rightarrow {\bf A}(P,S)\]
("если \(P\) суть \(Q\), а \(Q\) суть \(S\), то \(P\) суть \(S\)").
Подобный вывод и называется силлогизмом.
Аристотель установил, что логически приемлемыми является 19 таких комбинаций.
Правда в последствии оказалось, что 4 из них неявно подразумевают
обязательную истинность одного из свойств.
Например, т.н. силлогизм Darapti: \({\bf A}(P,Q),~~{\bf A}(P,S) \Rightarrow {\bf I}(Q,S)\) или:
\[
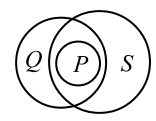\forall_x\, [P(x)\to Q(x)],~~\forall_x\, [P(x)\to S(x)] ~\Rightarrow~ \exists_x\, [Q(x)\,\&\, S(x)]
\]
корректен, если дополнительно \(\exists_x\, P(x)\). В противном случае, если \(P\)
пустое множество, то оно принадлежит \(Q\) и \(S\), но они могут не пересекаться.
Это приводит к тому, что из \(\forall_x\, [P(x)\to Q(x)]\),
\(\forall_x\, [P(x)\to S(x)]\) следует \(\exists_x\, [Q(x)\,\&\, S(x)]\),
только если добавить ещё и \(\exists_x\, P(x)\),
что стоит формально доказать при помощи резолюции.