ML: Логика и вероятность: Примеры теорий
Введение
Этот документ является факультативным приложением к введению
в математическую логику.
Мы рассмотрим несколько формальных теорий,
анализируя их аксиоматику и примеры логических выводов.
Кванторы и число объектов
✒ Фраза "существуют различные объекты находящиеся в отношении $R$" записывается следующим образом: $$ \exists_{x,y}\,\bigr[x\neq y~\,\&\,~R(x,y)\bigr]. $$ Кванторы $\exists_{x,y}$ c $x,y\in \{a_1,a_2,...\}$ "перебирают" соединения дизъюнкциями формулы $\bigr[a_i\neq a_j~\,\&\,~R(a_i,a_j)\bigr]$ для пар предметов. Члены с $i=j$ будут ложными: $(a_i\neq a_i) ~\equiv~\F $ и не влияют на результат $\F \vee Q ~\leftrightarrow~ Q$. Так, для трёх предметов $\{a_1,a_2,a_3\}$ получим: $ R(a_1,a_2)\vee R(a_1,a_3)\vee R(a_2,a_1)\vee R(a_2,a_3)\vee R(a_3,a_1)\vee R(a_3,a_2), $ что и означает утверждаемое в фразе.
✒ Фраза "любые различные объекты находятся в отношении $R$", требует импликации (если $x\neq y$, то ...): $$ \forall_{x,y}\,\bigr[x\neq y~\to~R(x,y)\bigr]. $$ Квантор общности - это цепочка формул, соединённых конъюнкцией. Для одинаковых предметов члены типа $a_1\neq a_1 ~\to~R(a_1,a_1)$ истинны и их можно опустить ($\T \,\&\,Q~\equiv~ Q$). Остаются только пары различных элементов.
Вообще, переводя с естественного языка на формальный,
нельзя путать импликацию и конъюнкцию.
Фраза "для любого положительного $x$
справедливо свойство $P$" записывается так: $\forall_x\,[(0 \lt x)\, \to\,P(x)]$.
Если поставить конъюнкцию, то
$\,\forall_x\,[(0 \lt x)~\,\&\,~P(x)]$ в арифметике будет ложным
(из-за $\forall_x$ при $x=0$).
Формула $\forall_x\,[(0 \lt x)~\vee~ P(x)]$ для $x\in \mathbb{N}=\{0,1,2,...\}$ эквивалентна $P(0)$,
что, также очевидно не о том.
Если же мы говорим, что "существует положительное $x$ со свойством $P$",
надо писать $\exists_x\,[(0\lt x)~\&~P(x)]$.
✒ Квантор существования $\exists_x P(x)$ сообщает, что есть один или несколько объектов, удовлетворяющих свойству $P$. Часто требуется фиксировать конкретное число объектов, фигурирующих в утверждении.
Фраза "не более одного объекта ($0$ или $1$) удовлетворяет свойству $P$",
записывается следующим образом:
$$
\forall_{x,y}\,\bigr[P(x)\,\&\,P(y)~\to~x=y\bigr].
$$
Соответственно можно определить квантор "существует в точности один объект обладающий свойством $P$":
$$
\exists^1_x\, P(x)~~~~~~~~\Leftrightarrow~~~~~~~~\exists_z\,P(z)~~\&~~\forall_{x,y}\,\bigr[P(x)\,\&\,P(y)~\to~x=y\bigr].
$$
Теперь символ $\exists^1_x$ можно использовать в формулах наравне с другими кванторами.
Аналогично, "по меньшей мере два объекта $(2,3,...)$ обладают свойством $P$" имеет вид:
$$
\exists_{x,y}\,\bigr[P(x)~\&~P(y)~\&~x\neq y\bigr],
$$
а "не более двух объектов $(0,1,2)$ обладают свойством $P$":
$$
\forall_{x,y,z}\,\bigr[P(x)~\&~P(y)~\&~P(z)~\to~(x=y~\vee~x=z~\vee~ y=z)\bigr].
$$
Конъюнкция двух последних формул даёт фразу
"в точности два объекта обладают свойством $P$", т.е. $\exists^2_x\,P(x)$.
Натуральные числа
Множество предметов со свойствами натуральных чисел $\mathbb{N}=\{0,1,2,...\}$
можно определить в сигнатуре с константой $0$ и
унарной (один аргумент) функцией, имеющей смысл следующего за числом $x$ числа $n(x)$.
Считаем, что в сигнатуре также есть отношение $x=y$ со стандартными свойствами (теория с равенством).
Пусть $n(x)$ - всюду определённая функция, т.е. для неё выполняется "нулевая аксиома":
$~~~\forall_x\,\exists^1_y\,[\,n(x)=y\,]$.
Для упрощения формул, кванторы общности, действие которых охватывает всю формулу, далее будут опускаться (но подразумеваться). Первые две аксиомы Пеано (PA), определяющие функцию $n(x)$, имеют вид:
$$ \begin{array}{llll} (\mathbf{N_1})& n(x) \neq 0 & ~~~~~ &-&\text{перед 0 нет числа} \\ (\mathbf{N_2})& n(x)=n(y) \to x=y & &-&\text{если числа совпадают, то предшествующие им числа равны} \\ \end{array} $$
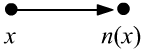 Аксиомы могут выполняться для различных
интерпретаций (в том числе, построенных на конечных множествах).
На рисунках предметные объекты ("числа") будем обозначать точками,
Аксиомы могут выполняться для различных
интерпретаций (в том числе, построенных на конечных множествах).
На рисунках предметные объекты ("числа") будем обозначать точками,
а функцию $n(x)$ - стрелкой,
соединяющей $x$ и значение $n(x)$. Так как $n(x)$ определена для всех $x$,
из каждой точки всегда должна выходить одна стрелка (всюду определённая функция).
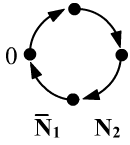 Аксиома ${\mathbf N_1}$ не выполняется на интерпретациях
в которых конечное число элементов, включающих $0$, соединены в кольцо,
т.к. в $0$ "попасть" нельзя
(черта над ${\mathbf N_1}$ означает, что она не выполняется). Аксиома ${\mathbf N_2}$
на этой интерпретации истинна.
Таким образом, ${\mathbf N_1}$ невыводима из ${\mathbf N_2}$.
Аксиома ${\mathbf N_1}$ не выполняется на интерпретациях
в которых конечное число элементов, включающих $0$, соединены в кольцо,
т.к. в $0$ "попасть" нельзя
(черта над ${\mathbf N_1}$ означает, что она не выполняется). Аксиома ${\mathbf N_2}$
на этой интерпретации истинна.
Таким образом, ${\mathbf N_1}$ невыводима из ${\mathbf N_2}$.
Аксиома ${\mathbf N_2}$ запрещает двум или более стрелкам скодиться в одной точке.
Справа аксиома ${\mathbf N_1}$ выполняется, а ${\mathbf N_2}$ - нет, поэтому
они взаимонезависимы.
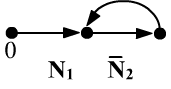 Одновременно аксиомы ${\mathbf N_1}$ и ${\mathbf N_2}$ выполняются только на бесконечных множествах.
Ниже приведено счётное множество предметов, образующих модель для ${\mathbf N_1}$ и ${\mathbf N_2}$.
Это множество разбивается на четыре несвязных подмножества $\mathbb{N}_0\cup\mathbb{N}_1\cup\mathbb{Z}_1\cup\mathbb{C}_1$:
Одновременно аксиомы ${\mathbf N_1}$ и ${\mathbf N_2}$ выполняются только на бесконечных множествах.
Ниже приведено счётное множество предметов, образующих модель для ${\mathbf N_1}$ и ${\mathbf N_2}$.
Это множество разбивается на четыре несвязных подмножества $\mathbb{N}_0\cup\mathbb{N}_1\cup\mathbb{Z}_1\cup\mathbb{C}_1$:
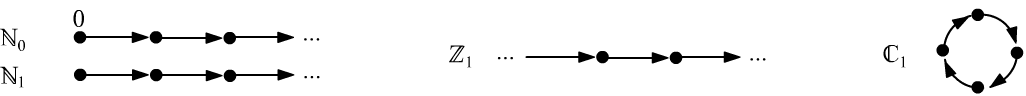
Множества $\mathbb{N}_0,\,\mathbb{N}_1$ являются "однонаправленными" бесконечными "последовательностями", причём $\mathbb{N}_0$ начинается с нуля, а $\mathbb{N}_1$ нуля не содержит. Их можно "сконструировать" при помощи рациональных чисел: $\mathbb{N}_0=\{0,\,1/2,...,\,n/(n+1),...\}$, $\mathbb{N}_1=\{1,\,1+1/2,...,\,1+n/(n+1),...\}$. Множество $\mathbb{Z}_1$ без начала и конца: $\mathbb{Z}_1=\{...,\,3-2/3,\,3-1/2,\,3,\,3+1/2,\,3+2/3,...\}$. Четвёртое множество $\mathbb{C}_1$ - это кольцо из любого конечного числа элементов.
Чтобы рассуждать о бесконечных последовательностях, необходима ещё одна аксиома, называемая аксиомой математической индукции. Она зависит от произвольного предиката $P(x)$: $$ (\mathbf{I})~~~~~~~~~~~~~P(0)~\to~\bigr(\,\forall_x\,\bigr[P(x)\to P(n(x))\bigr]~~\to~~ \forall_x\,P(x)\,\bigr). $$ На самом деле это "схема аксиом", т.е. бесконечное множество формул, c любыми мыслимыми свойствами $P(x)$. В силу правила modus ponens (MP): $P,~P\to Q~\Rightarrow~Q$, эта аксиома эквивалентна правилу вывода: $$ (\mathbf{Ind})~~~~~~~P(0),~~~~~\forall_x\,\bigr[P(x)\to P(n(x))\bigr]~~~~~\Rightarrow~~~~~ \forall_x\,P(x). $$ Оно означает, что если $0$ обладает свойством $P$ (база индукции) и для любого $x$, обладающего $P$ следует, что этим свойством обладает и следующее за ним число $n(x)$, то можно заключить, что свойством $P$ обладают все числа.
Покажем, что аксиома индукции запрещает модель типа $\mathbb{N}_0\cup\mathbb{N}_1$ с предыдущего рисунка, а, следовательно, независима от аксиом $\mathbf{N_1},\,\mathbf{N_2}$. Точнее докажем, что запрещены множества типа $\mathbb{N}_1$, в которых есть ненулевой элемент, не имеющий предыдущего:
Для любого ненулевого $x$ существует предшествующее ему число $y$.
$(1)$ В базе $P(0)$ посылка $0\neq 0$ ложна, поэтому, независимо от следствия, база $P(0)$ истинна $(\F\to A\equiv \T)$.
$(2)$ $P(n(x))$ равно $n(x)\neq 0~\to~\exists_y\,[\,n(y)=n(x)\,]$. Каков бы ни был $x$, следствие $\exists_y\,[\,n(y)=n(x)\,]$ истинно, т.к. существующий $y=x$. Поэтому $P(n(x))$ истинно и в силу $A\to \T\equiv \T$ истинно $P(x)\to P(n(x))$ при любом $x$. $\square$
Отметим, что в доказательстве аксиомы $\mathbf{N_1},~\mathbf{N_2}$ не участвовали.
Запретить последовательности $\mathbb{Z}_1$ или $\mathbb{С}_1$, не содержащих нуля, сложнее. Более того, можно доказать, что, какую бы аксиоматику мы не выбрали, всегда существуют интерпретации неизоморфные ряду натуральных чисел (т.н. нестандартные модели арифметики).
Сложение и умножение
Добавим в сигнатуру натуральных чисел бинарные (два аргумента) функции сложения $x+y$ и умножения $x\cdot y$. Пусть при любых $x,y$ свойства сложения индуктивно определяют следующие две аксиомы: $$ (\mathbf{A_1})~~~~~~~~~x+0 ~=~ x,~~~~~~~~~~~~~~~~~~~(\mathbf{A_2})~~~~~~~~~ n(x+y) ~=~ x+n(y). $$ Если в $\mathbf{A}_2$ положить $y=0$ и учесть $\mathbf{A}_1$, то получается $n(x)=x+1$, где $1=n(0)$ - новая предметная константа, отличная по $\mathbf{N}_1$ от $0$. Добавим её в сигнатуру. В результате, аксиомы для сложения и умножения можно записать в более "привычном" виде:
$$ \begin{array}{llll} (\mathbf{A_1})~~~ & x+0 ~=~ x,\\ (\mathbf{A_2})~~~& (x+y)+1 ~=~ x+(y+1),\\ \end{array} ~~~~~~~~~~~~~~~~~~~~~~~~ \begin{array}{llll} (\mathbf{M_1})~~~& x\cdot 0 ~=~ 0,\\ (\mathbf{M_2})~~~& x\cdot (y+1)~=~x+(x\cdot y).\\ \end{array} $$
Совокупность семи формул $\mathbf{N_1},\mathbf{N_2},\mathbf{I},\mathbf{A_1},\mathbf{A_2},\mathbf{M_1},\mathbf{M_2}$
составляют систему аксиом Пеано (PA) арифметики.
В качестве примера, выведем из этих аксиом коммутативность и ассоциативность функции сложения.
Пусть верно $P(x)$. Докажем истинность $P(x+1)$, записывая над равенством используемую при выводе формулу: $$ (x+1)+0 ~~\overset{\bf A_1}{=}~~x+1 ~~\overset{\bf A_1}{=}~~(x+0)+1 ~~\overset{P(x)}{=}~~(0+x)+1 ~~\overset{\bf A_2}{=}~~0+(x+1). $$ Равенство первого $(x+1)+0$ и последнего $0+(x+1)$ термов и есть формула $P(x+1)$. В результате из аксиом $\mathbf{A_1},~\mathbf{A_2}$ следует $P(x)\to P(x+1)$, поэтому выводима формула $\forall_x\,[\,P(x)\to P(x+1)\,]$, а по индукции $\mathbf{I}$ выводима $\forall_x\,P(x)$. $\square$
🔥 Это доказательство для краткости приведено в алгебраическом стиле. Запись $t_1=t_2=t_3$ - это сокращение, эквивалентное: $~~t_1=t_2,~~t_2=t_3~~~\Rightarrow~~~t_1=t_3$ (транзитивность). Первое равенство - это следствие аксиомы $\mathbf{A}_1$ (сейчас пишем квантор $\forall$, если он есть): $$ \forall_x\, (x+0=x)~~~~~\Rightarrow~~~~~x+0=x~~~~~\Rightarrow~~~~~(x+1)+0 = x+1, $$ где применены правила вывода $\forall_x\,Q(x)~~\Rightarrow~~Q(x)~~\Rightarrow~~Q(t)$ для терма $t=x+1$ (подстановка). Таким образом, мы имеем $\mathbf{A_1},~\mathbf{A_2},~P(x)~~\Rightarrow~~P(x+1)$, поэтому $\mathbf{A_1},~\mathbf{A_2}~~\Rightarrow~~P(x)\to P(x+1)$. Если только из аксиом теории следует некоторая формула с параметром, то на него можно навесить квантор общности (правило обобщения): $\text{Axioms}~~\Rightarrow~~~Q(x)~~\Rightarrow~~\forall_x\,Q(x)$. Действительно, если из $\text{Axioms}$ следует формула $Q(x)$ с параметром $x$, то она должна быть истинна всегда, когда истинны аксиомы, при любом значении $x$.
Докажем что из $P(x)$ следует $P(x+1)$: $$ (y+(x+1))+1 ~~\overset{\bf A_2}{=}~~ ((y+x)+1)+1 ~~\overset{ P(x)}{=}~~ ((y+1)+x)+1 ~~\overset{\bf A_2}{=}~~ (y+1)+(x+1). $$ Равенство первого и последнего термов, это формула $P(x+1)$, поэтому $P(x)\to P(x+1)$. $\square$
$$ x+(y+1)~~\overset{\bf A_2}{=}~~(x+y)+1~~\overset{P(y)}{=}~~(y+x)+1 ~~\overset{\bf AC_1}{=}~~(y+1)+x.~~~\square $$
Обратим внимание, что в $({\bf N_1,N_2,I,A_1,A_2})$ нет непосредственного утверждения о коммутативности сложения. По-видимому этому стоит удивиться.
Докажем в заключение ассоциативность сложения:
Геометрия
Рассмотрим в качестве второго примера часть аксиом Гильберта для планиметрии (двумерной геометрии).
Пусть есть два вида объектов - точки $x,y,...\in\mathcal{P}$ и прямые $\alpha,\beta...\in\mathcal{L}$.
Мы не наделяем их никакими образными свойствами.
Это элементы двух абстрактных множеств $\mathcal{P}$ и $\mathcal{L}$.
Констант и функций в теории не будет.
В качестве первого предиката возьмем предикат равенства объектов одного множества $x=y$ или $\alpha=\beta$.
Неравенство определяется при помощи логического отрицания: запись $x\neq y$ это сокращение для $\neg(x=y)$.
Второй предикат $(x\in\alpha)$ в "неформальной геометрии" соответствует
фразам: "точка $x$ принадлежит прямой $\alpha$" или
"прямая $\alpha$ проходит через точку $x$".
Для сокращения мы будем также использовать производные предикаты
$(x,y\in\alpha)$ - это $~(x\in\alpha)\,\&\,(y\in\alpha)$ (точки $x,\,y$ лежат на прямой $\alpha$)
или $(x\in \alpha,\beta)$ - это $~(x\in\alpha)\,\&\,(x\in\beta)$ (прямые $\alpha$ и $\beta$
пересекаются в точке $x$).
Так как в формальной теории не должно быть "очевидных", неявно подразумеваемых утверждений, свойства предиката $(x\in\alpha)$ следует однозначно задавать при помощи предметных аксиом.
Через любые две точки $x,y$ проходит прямая $\alpha$ (возможно не одна).
Отсюда следует, что через любую точку проходит хотя бы одна прямая: $\forall_x \,\exists_\alpha \,(x\in\alpha)$ т.к, в парах $(x,y)$ для $\forall_{x,y}$ есть диагональные $(x,x)$, которые также должны быть истинными. Это правило $\forall_{x,y}\,A(x,y)~\Rightarrow\forall_x \,A(x,x)$.
Через любые две различные точки $x,y$ проходит не более одной прямой ($0$ или $1$).
Вместе $\mathbf{A_1}\,\&\,\mathbf{A_2}$ означают, что "через две различные точки должна проходить одна и только одна прямая".
На любой прямой $\alpha$ находится по меньшей мере две различные точки $x,y$.
Существует по меньшей мере три различные точки $x,y,z$ не принадлежащие одной прямой $\alpha$.
Сокращённая запись $x\neq y\neq z$ означает конъюнкцию трёх предикатов: $(x\neq y)\,\&\,(x\neq z)\,\&\,(y\neq z)$
и, как и в предыдущей аксиоме, под квантором существования оставляет только различные $x,y,z$.
Эта аксиома требует уже не менее трёх точек и "двух измерений" ($\mathbf{A_1}$-$\mathbf{A_3}$
выполняются и для точек, лежащих на единственной прямой).
При этом не обязательно существование таких точек для каждой прямой. Достаточно хотя бы одной тройки.
Из $\mathbf{A_4}$ следует, что для любой прямой есть хотя бы одна точка которая не ней не находится:
$\forall_\alpha\,\exists_x\,\neg(x\in \alpha)$.
Действительно, те три, существующие по $\mathbf{A_4}$ точки, либо не находятся на данной прямой $\alpha$,
либо на ней находится не более двух из них $\square$.
В принципе, вместо аксиомы $\mathbf{A_4}$ можно взять формулу $\forall_\alpha\,\exists_x\,\neg(x\in \alpha)$,
так как вместе с $\mathbf{A_3}$ она даёт сильную версию $\mathbf{A_4}$.
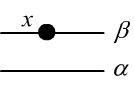 Для записи пятой аксиомы о параллельных, определим предикат от трёх аргументов:
$$
\text{Par}(x,\alpha,\beta):~~~~~~(x\in\beta)~\,\&~\neg \exists_y (y\in\alpha,\beta),
$$
означающий: "через точку $x$ проходит прямая $\beta$, параллельная к прямой $\alpha$".
Параллельность понимается в смысле отсутствия общих точек у прямых ("не существует общей точки $y$ для прямых $\alpha$ и $\beta$").
Как и любой предикат, при одних значениях аргументов, он может быть истинным, а при других - ложным.
Для записи пятой аксиомы о параллельных, определим предикат от трёх аргументов:
$$
\text{Par}(x,\alpha,\beta):~~~~~~(x\in\beta)~\,\&~\neg \exists_y (y\in\alpha,\beta),
$$
означающий: "через точку $x$ проходит прямая $\beta$, параллельная к прямой $\alpha$".
Параллельность понимается в смысле отсутствия общих точек у прямых ("не существует общей точки $y$ для прямых $\alpha$ и $\beta$").
Как и любой предикат, при одних значениях аргументов, он может быть истинным, а при других - ложным.
Для любой точки $x$ и прямой $\alpha$, которой $x$ не принадлежит, проходит не более одной ($0$ или $1$) прямой, параллельной $\alpha$.
Для полного описания планиметрии необходимы также отношение "между" $B(x,y,z)$: "точка $y$ находится между точками $x$ и $y$" и отношение конгруэнтности (геометрическое равенство отрезков и углов). Их свойства также задаются соответствующими группами аксиом. Из этих аксиом можно вывести теорему:
Параллельных прямых должно быть не менее одной.
Поэтому, вместе с $\mathbf{A_5}$ имеем евклидово утверждение $\mathbf{E}=\mathbf{A_5}\,\&\,\mathbf{T_5}$ о том, что параллельная к $\alpha$ прямая $\beta$, проходящая через точку $x$, не лежащую на $\alpha$, всегда одна и только одна.
Анализ аксиом геометрии
Покажем непротиворечивость сформулированных выше пяти аксиом геометрии для отношения $(x\in\alpha)$:

На первом рисунке (модели) все пять аксиом истинны. Подчеркнём, что рисунок не несёт никакой геометрической нагрузки и играет лишь роль перечисления объектов и истинностных значений предиката $(x\in\alpha)$. Так, для точек и прямых выбраны множества из трёх элементов: $\mathcal{P}=\{a,b,c\}$ и $\mathcal{L}=\{\alpha,\beta,\gamma\}$. На этих множествах заданы значения истинности предиката так, что $(b\in\alpha)\equiv (c\in\alpha)\equiv \T $, а $(a\in\alpha)\equiv \F $ и т.д. Так как $\mathbf{A_5}$ разрешает отсутствие параллельных прямых ("не более одной"), то она на этой интерпретации также истинна. А вот теорема Евклида $\mathbf{E}$ ложна (нет параллельных прямых), что помечено чертой над $\mathbf{E}$. Аналогична вторая модель.
В третей модели есть четырые точки и шесть прямых: $\mathcal{L}=\{\alpha,\beta,\gamma,\delta,\sigma,\epsilon\}$. На этой интерпретации истинны как $(\mathbf{A_1}-\mathbf{A_5})$, так и $\mathbf{E}$. Параллельными прямыми являются: $(\alpha,\epsilon)$, $(\beta,\delta)$ и $(\gamma,\sigma)$. Обратим внимание, что в центре прямые не пересекаются (точками являются только чёрные кружки). Четвёртая модель изоморфна третей.
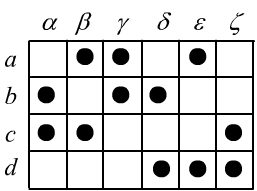 Изоморфизм двух моделей в данном случае означает, что существуют перестановки точек $x'=f(x)$ и прямых $\alpha'=g(\alpha)$
при которых $(x\in\alpha)~\leftrightarrow~(x'\in\alpha')$ для всех $x$ и $\alpha$.
Например, интерпретация на последней картинке описывается таблицей, приведенной справа (точка - отношение истинно).
В данном случае возможно $720$ неэквивалентных перестановок строк и колонок этой таблицы,
а, следовательно, $720$ изоморфных интерпретаций.
Изоморфизм двух моделей в данном случае означает, что существуют перестановки точек $x'=f(x)$ и прямых $\alpha'=g(\alpha)$
при которых $(x\in\alpha)~\leftrightarrow~(x'\in\alpha')$ для всех $x$ и $\alpha$.
Например, интерпретация на последней картинке описывается таблицей, приведенной справа (точка - отношение истинно).
В данном случае возможно $720$ неэквивалентных перестановок строк и колонок этой таблицы,
а, следовательно, $720$ изоморфных интерпретаций.
Приведём интерпретации, доказывающие независимость аксиом $(\mathbf{A_1}-\mathbf{A_5})$ (чертой помечаем ложную в данной интерпретации аксиому):

Естественно в последнем случае прямые пересекаются только на "жирных точках", т.е. в этой интерпретации есть пять точек и десять прямых. В частности, к прямой $\alpha$ параллельны две прямые $\beta$ и $\gamma$.
Иногда теоремы геометрии имеют очень похожие формулировки, но при этом являются
логически независимыми утверждениями.
Например:
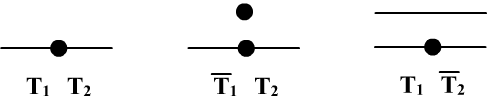
- $(\mathbf{T_1})~~~$ "Каждая точка лежит на некоторой прямой" $~~~~~\forall_x\,\exists_\alpha\,(x\in \alpha)$
- $(\mathbf{T_2})~~~$ "На каждой прямой лежит некоторая точка" $~~~~~\forall_\alpha\,\exists_x\,(x\in \alpha)$
Приведенные выше аксиомы не образуют полной теории, хотя в целом геометрия на плоскости полна. Для получения полной теории, необходимо добавить ещё два отношения и соответствующие им аксиомы. Неполнота аксиом $(\mathbf{A}_1-\mathbf{A}_5)$ в частности следует из существования конечных неизоморфных моделей этой теории.
При построении геометрии можно выбирать другие сигнатуры и аксиомы. Например, в аксиоматике Тарского существуют только точки. Их свойства задают три базовых предиката: равенства $x=y$, конгруэнтности $(x,y \cong u,v)$ и нахождения между $B(x,y,z)$. Прямая (точнее отрезок) определяется двумя точками $\alpha=(x,y)$, а квантор принадлежности это $z\in\alpha ~~\Leftrightarrow~~B(x,z,y)$. Семантически конгруэнтность $(x,y \cong u,v)$ означает равенство длин отрезков $(x,y)$ и $(u,v)$. Аксиомы Тарского определяют свойства этих предикатов. Например, для любых точек конгруэнтность "рефлексивна" $(x,y \cong y,x)$, транзитивна $(x,y \cong u,v)\,\&\,(x,y \cong s,t)~\to~(u,v \cong s,t)$ и "идентична" $(x,y \cong z,z)~\to~x=y$ (нулевой отрезок).
Немного философии
Теория множеств в некотором смысле особенная теория. Ранее, рассматривая формальные теории, мы ссылались на множества предметов по которым "пробегались" кванторы $\forall_x$ и $\exists_x$. Очевидно, что при построении аксиоматики теории множеств такой подход не годится.
Теория множеств должна строиться как игра в слова в чистом виде.
Нет истинных или ложных утверждений.
Нет причин сомневаться в существование любых
объектов, коль эти объекты определены в виде слов. Произнесенное слово уже существует.
Можно считать, что некоторые слова (объекты) недопустимы (не существуют).
Но это будет уже другая (вполне возможно также допустимая) игра в слова.
Впрочем, если в процессе порождения слов возникают противоречия,
правила игры или исходные слова (аксиомы) необходимо, конечно, менять.
Например, пусть есть сигнатура c отношением $B(x,y)$, свойства которого определяет единственная аксиома: $\exists_b\,\forall_x\,\bigr[\,B(b,x)~\leftrightarrow~\neg B(x,x)\,\bigr]$. Она утверждает существование некоторого объекта $b$. Содержательно эта теория соответствует истории про брадобрея $b$ который бреет всех таких и только таких $x$ которые не бреются сами. Несложно видеть, что эта теория противоречива (когда любой $x$ равен $b$). Поэтому она бессмысленна и такого брадобрея не существует, хоть его определение и написано. Заметим, что если убрать оборот " и только таких" (заменив $\leftrightarrow$ на $\to$), теория сразу станет осмысленной, а брадобрей существующим и не бреющимся $~~\Rightarrow~\neg B(b,b)$. А при фразе "каждого, который не бреется, бреет брадобрей": $\neg B(x,x)~\to~B(b,x)$, брадобрей бреется $\Rightarrow~~ B(b,b)$.
Большинство математиков являются платонистами и верят в объективное существование математических конструкций и априорную истинность или ложность математических утверждений. Как и любая философия, она выглядит подозрительной, однако сомневающийся в существовании написанного слова становится ещё большим платонистом, чем тот, кто его написал. Поэтому будем считать, что "существуют" актуально бесконечные множества и множества всех их подмножеств, коль определения этих объектов записаны на бумаге. При этом к неприятностям необходимо всегда быть готовым.
Множества
Будем иметь дело с объектами $x,y,z,...$, которые в семантическом подходе интерпретируются как множества. Ничего кроме множеств не существует. Все математические конструкции (числа, точки и т.п.) определяются как множества специального вида. Множества могут совпадать $x=y$ и одно множество может принадлежать другому: $x\in y$, что бы это не означало (в сигнатуре теории есть два отношения).
Часть идущих далее аксиом не являются независимыми и это будет помечаться штрихом. Тем не менее декларируемые в них утверждения являются концептуально важными. Несмотря на то, что все рассуждения о множествах можно проделывать чисто синтаксически (игра в слова), мы будем упрощать себе жизнь, используя семантику. В наших полуформальных рассуждениях будут использованы понятия истины и лжи, а также обычная булева и кванторная алгебры.
Если два множества $x,y$ содержат одни и те же элементы, то они равны.
Эта аксиома объёмности в "наивной теории множеств" означает, что совокупность $\{a,b,a,a,a\}$ тоже самое, что множество $\{a,b\}$. Другими словами множество - это объединение попарно различимых элементов, каждый из которых находится в единственном числе и порядок перечисления элементов в множестве роли не играет.
Так как $A\leftrightarrow B$ эквивалентно $(A\to B)\,\&\,(B\to A)$, при помощи правила объединения, посылку аксиомы можно переписать следующим образом: $\forall_z(z\in x~\to~z\in y)~~\&~~\forall_z(z\in y~\to~z\in x)$. Импликация под квантором общности из "всех возможных" $z$ "отбирает" только те, которые принадлежат $x$ (тогда они принадлежат и $y$) и наоборот. Это и означает, что $x,y$ "содержат" одинаковые элементы. Используя базовый символ сигнатуры, определим отношения "$x$ подмножество $y$" и "$x$ строгое подмножество $y$": $$ x \subseteq y~~~~~\Leftrightarrow~~~~~\forall_z\,(z\in x ~~\to~~z\in y),~~~~~~~~~~~~~~~~~~~~~~ x\subset y~~~~~\Leftrightarrow~~~~~x\subseteq y~\&~x\neq y. $$ Теперь первую аксиому можно переписать в следующем виде: $x\subseteq y~\,\&\,~y\subseteq x~~\to~~x=y$. Очевидно, что $x\subseteq x$.
В "наивной теории множеств" например $\{a,b\} \subset \{a,b,c\}$. При этом $a\in \{a,b\}$, но $a\not\subset \{a,b\}$, а вот $\{a\}\subset\{a,b\}$. Другими словами внутри $\{...\}$ перечисляются элементы множества. Часть из них снова в фигурных скобках образуют подмножество. При этом важно отличать $a$ и $\{a\}$ (множество из одного элемента $a$).
Строгое подмножество обладает свойствами строгого порядка. Для любых $x,y,z$ оно антирефлексивно, транзитивно и асимметрично (последнее выводится из первых двух свойств): $$ \neg(x\subset y),~~~~~~~~~~~x\subset z~\to~(z \subset y ~\to~x\subset y),~~~~~~~~~~~~~x\subset y ~\to~\neg(y\subset x). $$
Аксиомы Цермело-Френкеля
Последующие аксиомы утверждают факт "существования" тех или иных множеств. При этом важно, что каждое новое множество получается из уже построенных (ранее определённых) множеств. Это позволяет избежать ряда "парадоксов" наивной теории множеств.
Любые два множества $x,y$ и только они могут быть элементами множества $s$.
Существующее по аксиоме пары множество из двух элементов обозначается как $s=\{x,y\}$. Фигурные скобки в данном случае играют роль предметных функций с произвольным числом аргументов. В частности, эта же аксиома "разрешает" существование и одноэлементных множеств $\{x\}$ (когда $x$ и $y$ совпадают).
Впрочем, существование хотя бы одного множества следует из рефлексивности равенства: $\forall_x\,(x=x)$ и общезначимой формулы $\forall_x P~\to~\exists_x\,P$, дающих $\exists_x\,(x=x)$.
Два элемента множества $\{x,y\}$ неупорядочены: $\{y,x\}$ это тоже, что и $\{x,y\}$. Однако при помощи пары можно определить упорядоченную пару $(x,y)$ следующим образом: $(x,y)~=~\{~\{x\},~\{x,y\}~\}.$ При этом $(y,x)\neq (x,y)$.
Для любого множества $x$ существует его подмножество $s$, все элементы которого обладают свойством $P$.
Ключевым в этой аксиоме выделения является использование уже существующего множества $x$ для построения (выделения из $x$) множества $s$. В "наивной теории множеств" эта аксиома выглядела так: $\exists_s\,\forall_z\,\bigr[\,P(z) ~\leftrightarrow~z\in s\,\bigr]$. Если в ней вместо $P(z)$ положить $z\not\in z$, эквивалентное $\neg(z\in z)$ , то получится $\exists_s\,\forall_z\,\bigr[\,z\not\in z ~\leftrightarrow~z\in s\,\bigr]$, или при $z=s$ (т.к. $z$ любое) - противоречие, называемое парадоксом Рассела. В $\mathbf{ZF_P}$ такого противоречия не возникает.
Подмножество элементов с данным свойством обозначается следующим образом: $y=\{z\mid z\in x~\&~P(z)\}$.
Естественно, аксиома $\mathbf{ZF_P}$ является схемой аксиом, т.е. бесконечным набором формул с различными $P(z)$.
Докажем при помощи $(\mathbf{ZF_P})$ следующее важное утверждение:
Существует пустое множество $s$, не содержащее других множеств.
Для этого положим вместо $P(z)$ формулу $z\neq z$. Так как она тождественно ложна, то по $\mathbf{ZF_P}$ ложным должно быть и $z\in s$ или истинным $z\not\in s$.
Существующее множество $s=\varnothing=\{\}=\{z\mid \F\}$ со свойством $\forall_z\,(z\not\in\varnothing )$ единственно и его можно включить в сигнатуру. Единственность непосредственно следует из аксиомы $\mathbf{ZF_=}$: два $\varnothing$ и $\varnothing'$ состоят из одинаковых, хоть и отсутствующих элементов, следовательно совпадают. Покажем это чуть более формально. Отношение $\varnothing \subseteq \varnothing'$, равное $\forall_z(z\in \varnothing~\to~z\in \varnothing')$, истинно (т.к. посылка ложна). Аналогично истинно $\varnothing' \subseteq \varnothing$. Поэтому по $(\mathbf{ZF_=})$ эти множества совпадают: $\varnothing = \varnothing'$.
Напомним, что $\varnothing=\{\}$ и $\{\varnothing\}=\{\{\}\}$ разные множества ("пустая коробка и коробка в которой пустая коробка"). Пустое множество является подмножеством любого множества: $\varnothing\subseteq y$ т.к. посылка в $\forall_z\,(z\in \varnothing ~\to~z\in y)$ ложна.
Существует множество $s$ равное объединению всех множеств содержащихся в данном множестве $x$.
Семантически аксиома объединения означает, что если есть, например, двухэлементное множество $\{\{a\},~\{b,c\}\}$, мы можем построить трёхэлементное множество: $\{a,~b,~c\}$ и т.д. Такое множество, получаемое "вытряхиванием" множеств из элементов $x$, обозначают как $\cup x = \{z\mid \exists_w\,(~z\in w\,\&\,~w\in x)\}$. С его помощью можно определить: $$ x\cup y ~~~~\Leftrightarrow~~~~\cup\{x,y\}~~~~\Leftrightarrow~~~~\{z\mid z\in x \vee z\in y\}. $$ В частности $\{a\}\cup \{b,c\} ~=~\{a,b,c\}$ и т.д.
Для любого множества $x$ существует множество $s$, состоящее из всех подмножеств $x$ и только из них.
Эта аксиома степени для данного $x$ разрешает множество $s=\{z\mid z\subseteq x\}$. Такое множество обозначают как $2^x$.
Обратим внимание, что во всех аксиомах "существования" множества $s$ стоит символ эквивалентности $\leftrightarrow$ ("тогда и только тогда"), а не импликации $\to$ ("если, то"). Поясним это на последней аксиоме. Формула $z\subseteq x ~\to~z\in s$ означает, что "любое подмножество $z$ множества $x$ является элементом $s$". Но если $z$ не подмножество $x$, то $z\in s$ может быть как истинным, так и ложным. Другими словами эта формула говорит, что множество $s$ состоит из всех подмножеств $x$ и возможно ещё из каких-то других элементов. Обратная импликация $z\in s ~\to~z\subseteq x$ утверждает, что все элементы $s$ являются подмножествами $x$, но при этом не обязательно всеми подмножествами. Только объединение этих двух формул $(A \to B)\,\&\,(B\to A)$ в $A \leftrightarrow B$ приводит к "$s$ состоит из всех подмножеств $x$ и только из них". В принципе, можно использовать и ослабленную версию этой аксиомы (без "и только из них").
Предыдущие шесть утверждений декларировали существование конечных множеств с любым числом элементов. Следующая аксиома разрешает существовать бесконечным множествам.
Существует множество $s$ с бесконечным числом элементов.
Аксиома бесконечности индуктивно вводит актуальную бесконечность,
как законченную совокупность $s$.
Сначала утверждается, что множеству $s$ принадлежит некоторый произвольный
элемент $x$ (например, $\varnothing$).
Затем, что любой элемент $z$ множества $s$ принадлежит хотя бы одному элементу $w$ того же множества $s$.
Например, если есть $\varnothing$, то должен быть и $\{\,\varnothing\,\}$,
но тогда должен быть и
$\{\,\{\,\{\varnothing\}\,\}\,\}$ и т.д. сколько угодно долго.
Каждое непустое множество $x$ содержит элемент $z$ который не имеет общих с $x$ элементов.
Аксиому регулярности (фундирования) при помощи функции пересечения множеств $x\cap y = \{\,z\mid z\in x~\&~z\in y\,\}$
можно записать в виде: $x\neq \varnothing ~\to~\exists_z\,(z\in x ~\&~z\cap x=\varnothing)$.
Смысл её в том, что в любом непустом множестве $x$ найдётся элемент $z$
"минимальный" относительно отношения $\in$
(т.е. нет $w$ с таким же свойством $w\in x$).
В множестве $x=\{\{a,b\},~a\}$ такой $z=a$. При этом $a$ не может зависеть от себя же (см. ниже).
Она также запрещает более хитрые рекурсивные связи. Если $x=\{a,\,b\}$, то $(a\not\in b~\vee~b\not\in a)$.
Из аксиом регулярности и пары
следует что ни какое множество
не может быть своим элементом: $z\not\in z$.
От противного: пусть $z\in z$.
По аксиоме пары есть множество $x=\{z\}$.
Оно не пустое и поэтому $z\cap x=\varnothing$.
Но это не так, поскольку $z\in z$ и $z\in x$, т.е. $z$ принадлежит пересечению.
Из этой же аксиомы следует, что не существует бесконечной цепочки вложенных множеств: $ ... \in x_2 \in x_1$, т.е. число парных фигурных скобок всегда конечно.
Пусть конечное множество $x$, состоит из $n$ непустых, непересекающихся множеств $w$. "Очевидно", что взяв из каждого множества $w$ по элементу $z$, можно построить новое множество $s$ с $n$ элементами. Это множество будет пересекать каждое исходное множество ровно на одном элементе. Для бесконечного числа множеств такой способ построения нового множества не вполне "самоочевиден" и должен регламентироваться аксиомой выбора.
Натуральные числа как множества
В платоновском мире математических идей нет ничего кроме множеств. Любые сущности, которые в наивной теории множеств были элементами множеств, но сами множествами не являлись, теперь должны определяться через множества. Таким образом вся математика далее строится при помощи слов о множествах. Определим, например, множество натуральных чисел $\mathbb{N}=\{0,1,2,...\}$, используя идею фон-Неймана.
Пусть множество $\varnothing$ эквивалентно числу $0$. Введём множество из одного элемента: $\{0\}$ или $\{\, \varnothing \,\}$. Все остальные натуральные числа будем строить по схеме: если $x\in \mathbb{N}$, то $n(x)=x+1~=~x\cup \{x\}$ также принадлежит $\mathbb{N}$: $$ 0:=\varnothing,~~~~~~~1:=\{0\}=\{\, \varnothing \,\},~~~~~~~~~2:=\{0,1\}=\{\, \varnothing,~ \{\, \varnothing \,\} \,\}, ~~~~~~~~ 3:=\{0,1,2\} = \{\, \varnothing,~ \{\, \varnothing \,\},~\{\, \varnothing,~ \{\, \varnothing \,\} \,\} \,\}. $$ Их объединение образует $\mathbb{N}$. Естественно, необходимо далее показать, что введенные подобным образом слова обладают привычными арифметическими свойствами. Например, сразу видно, что они линейно упорядочены, где в качестве отношения порядка выступает отношение строго подмножества: $x\lt y~~\Leftrightarrow~~x\subset y$ (пустое множество является подмножеством любого множества): $$ 0 ~\lt~1~~~\Leftrightarrow~~~ \varnothing \subset \{\,\varnothing\,\},~~~~~~~~~~~~ 1 ~\lt~2~~~\Leftrightarrow~~~ \{\varnothing\} \subset \{\varnothing,~\{\varnothing\}\},~~~~~~~~~~~~ 0 ~\lt~2~~~\Leftrightarrow~~~ \varnothing \subset \{\varnothing,~\{\varnothing\}\},... $$ Линейный порядок означает, что для любых $x,y$ справедливо $(x\lt y) \vee (y\lt x) \vee (x=y)$. Отметим, что для данной совокупности множеств линейный порядок задаёт и отношение $x\in y$ (хотя в общем случае для него транзитивность $x\in y~\&~y\in z~\to x\in z$ не выполняется).
Если бы мы определили числа как множества
$0:=\varnothing,~~1:=\{\varnothing\},~~2:=\{\{\varnothing\} \},~~
~~3:=\{\{\{\varnothing\}\}\}$, то линейный порядок нельзя было бы ввести,
ни при помощи подмножеств, ни при помощи принадлежности ($0\not\in 2$).
Другой способ
$~~~0:=\varnothing,~~1:=\{\varnothing\},~~2:=\{\varnothing,~\{\varnothing\} \},
~~3:=\{\varnothing,~\{\varnothing\},~\{\{\varnothing\}\}\}, ....$,
линейно упорядочен по $x\subset y$, но в нём сложно компактно выразить $n+1$ через $n$.
Упорядоченные множества
Отношения in и on