ML: Теория Демпстера-Шафера

Введение

В теории Демпстера-Шафера (ТДШ) для меры истинности утверждения $A$ используется интервальная оценка $[a,~1-\bar{a}]$, где нижняя граница $a$ называется доверием и равна сумме фактов поддерживающих утверждение, а верхняя граница, называемая правдоподобием, равна $1-$ сумме фактов противоречащих утверждению $A$, т.е.поддерживающих его отрицание $\bar{A}$. Если нет поддерживающих утверждение фактов, то нижняя граница (доверие) равна нулю, а если нет и противоречащих утверждению фактов, то верхняя граница (правдоподобие) равна единице. Такая ситуация $[0,1]$ соответствует полной неопределённости ("или встречу динозавра, или не встречу").

Возможность различать неопределённость $[0,1]$ и равновероятность $[0.5,~0.5]$ важна при проведении рассуждений. Например, в методе Байеса, если априорная вероятность события $A$ неизвестна, обычно считают, что $P(A)=1/2$. Этот же выбор мы вынуждены делать для "истинно равновероятного" события (подбрасывания монеты). Теория Демпстера-Шафера позволяет различать эти две ситуации.

Интервал истинности события

Рассмотрим в качестве примера утверждение о том, что "внутри сундука находится шкатулка" (сундук закрыт).
Есть две взаимоисключающие гипотезы: $A$:"находится" и $\bar{A}$: "не находится". Интервалы этих истинности этих гипотез могут пересекаться или не пересекаться:

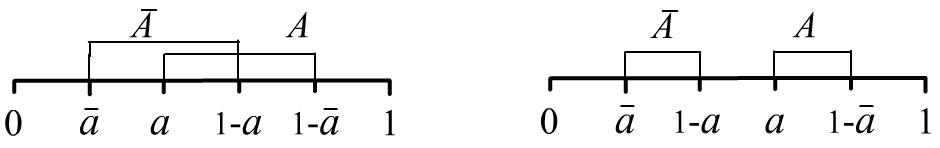
На первом рисунке $a\lt 1/2$, а на втором $a\gt 1/2$ и в обоих случаях $\bar{a}\lt a$. Ещё два варианта соответствуют перестановке $A$ и $\bar{A}$. Когда интервалы не пересекаются и $a=1-\bar{a}$, мы получаем обычные точечные вероятности $P(A)=a$ и $P(\bar{A})=\bar{a}$.

Так как в интервале $A:~[\text{Bel}(A),~1-\text{Bel}(\bar{A})]=[a,\,1-\bar{a}]$ верхняя граница интервала должна быть не ниже нижней, то необходимо соблюдать следующее ограничение: $$ \text{Bel}(A) + \text{Bel}(\bar{A}) \le 1. $$

Для большого числа взаимоисключающих утверждений $\{H_1,...,H_n\}$, отслеживать подобные неравенства для поддержания непротиворечивости теории уже непросто. Собственно задачей ТДШ является построение способа согласования границ интервалов оценки истинности различных утверждений.

Массовые функции

Пусть есть множество взаимоисключающих утверждений (гипотез): $\mathbb{H}=\{H_1,...,H_n\}$, так что $H_i\,\&\,H_j = \mathbb{F}$ (ложь) для всех $i\neq j$. В ТДШ такое множество называется фреймом различений (frame of discernment) или универсальным множеством. В частности, множество $\mathbb{H}$ может состоять из элементарных событий.

Рассмотрим все подмножества множества $\mathbb{H}$. Их можно нумеровать $n$-значными бинарными числами $101...1$ (в данное подмножество гипотеза $H_1$ включена, гипотеза $H_2$ не включена и т.д.). Таких чисел будет $2^{|\mathbb{H}|}$, где $|\mathbb{H}|=n$ - число элементов множества $\mathbb{H}$. Множество всех подмножеств принято обозначать как $2^{\mathbb{H}}=\{\,A\mid A\subseteq \mathbb{H}\,\}$, где перед чертой стоит элемент, а после черты условие которому он удовлетворяет.

◊ Для $\mathbb{H}=\{H_1,H_2,H_3\}$ существует восемь подмножеств (включая пустое множество $\varnothing$ и само $\mathbb{H}$): $$ 2^{\mathbb{H}} ~=~ \{~ \varnothing,~\{H_1\},~\{H_2\},~\{H_3\},~\{H_1,H_2\},~\{H_1,H_3\},~\{H_2,H_3\},~\mathbb{H}~ \}. $$

Подмножества трактуются как объединение гипотез при помощи логического исключающего или: $H_1\oplus H_2$, т.е. $\{H_1,H_2\}$ означает, что верно или $H_1$, или $H_2$ (что-то одно). Отрицание гипотезы $\bar{H}_1$ означает, что истинно всё что угодно кроме неё, т.е. $\{~\{H_2\},~\{H_3\},~\{H_2,H_3\}~\}$ (всё, не содержащее $H_1$).

Предполагается, что существуют эксперты, каждый из которых может выбрать одно из подмножеств как верное. Долю экспертов "проголосовавших" за данное подмножество $A\in 2^{\mathbb{H}}$ назовём массой его поддержки $m(A)$. Считаем, что каждый эксперт выбор сделал, поэтому: $$ m(\varnothing)=0,~~~~~~~~m(A) \ge 0,~~~~~~~~\sum_{A\,|\,A\,\in \,2^{\mathbb{H}}} m(A) = 1. $$ Вместо экспертов часто говорят о сумме (массе) свидетельств в поддержку данного подмножества. Подмножества для которых $m(A) \gt 0$ называют фокальными элементами (focal elements), а их объединение - ядром.

◊ Пусть в примере с тремя гипотезами распределение голосов экспертов по подмножествам имеет вид: $$ \begin{array}{r|l|l|l|l|l|l|l|l|} A: & \varnothing & \{H_1\} & \{H_2\} & \{H_3\} & \{H_1,H_2\} & \{H_1,H_3\} & \{H_2,H_3\} & \mathbb{H}\\ \hline m(A): & 0 & 0.1 & 0.4 & 0 & 0.2 & 0 & 0.3 & 0 \end{array} $$ Так, не нашлось ни одного голоса за $H_3$, но при этом $30\%$ экспертов считают, что верно или $H_2$, или $H_3$.
Кроме этого, $\mathbb{H}=\{H_1,H_2,H_3\}$ не получило ни одного голоса в поддержку. Фокальными элементами являются $\{H_1\}$, $\{H_2\}$, $\{H_1,H_2\}$, $\{H_2,H_3\}$, а ядро (их объединение) совпадает с $\mathbb{H}$.

Доверие

Ключевым для TДШ понятием является функция доверия подмножества $A$ (belief function). Она обозначается как $\text{Bel}(A)$ и равна суммарной массе всех подмножеств гипотез, входящих в $A$: $$ \text{Bel}(A) ~=~ \sum_{S\,\mid\, S\subseteq A} m(S) ~=~ m(A)~+~\sum_{S\,\mid\, S\subset A} m(S). $$

◊ Вычислим в примере с тремя гипотезами значения доверия некоторых множеств: $$ \begin{array}{lcll} \text{Bel}(H_1) &=& m(H_1) = 0.1,\\ \text{Bel}(H_1,H_2) &=& m(H_1) + m(H_2) + m(H_1,H_2) = 0.1+0.4 + 0.2 = 0.7, \\ \text{Bel}(H_1,H_3) &=& m(H_1) + m(H_3) + m(H_1,H_3) = 0.1+0 + 0 = 0.1, \\ \text{Bel}(H_1,H_2,H_3) &=& 1 \text{ (что то одно истинно)}. \end{array} $$

Функция доверия всех гипотез всегда равна единице: $\text{Bel}(\mathbb{H})=1$, а доверие к гипотезе равно её массе $\text{Bel}(H_i)=m(H_i)$. Несложно видеть, что зная доверия всех подмножеств, можно восстановить их массы: $$ m(\varnothing)=0,~~~~~~~~~m(A)~=~\text{Bel}(A) - \sum_{S\,\mid\, S\subset A} m(S) ~=~ \sum_{S\,\mid\, S\subseteq A} (-1)^{|A-S|}\,\text{Bel}(S). $$

Отметим, что, любое подмножество $B\subset A$ представляет более сильное утверждение (более конкретное), чем $A$. Обычно, оно требует более веских доказательств для его поддержки. Тем не менее, даже если $m(B)\gt m(A)$, доверие к $A$ всегда будет не ниже: $\text{Bel}(B)\le \text{Bel}(A)$.

Правдоподобие

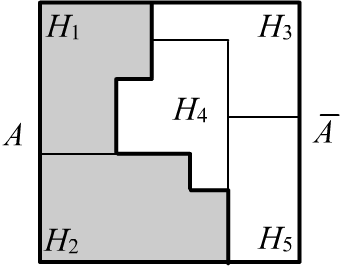Пусть множество $\mathbb{H}$ состоит из пяти гипотез, а событие (утверждение) $A=\{H_1,H_2\}$.
Тогда отрицание $\bar{A}=\{H_3,H_4,H_5\}$. В результате событие $A$ и его отрицание $\bar{A}$ разбивают пространство гипотез $\mathbb{H}$ на две непересекающиеся части. Понятно, что доверие отрицания $\bar{A}$ равно сумме масс всех подмножеств $2^{\mathbb{H}}$, которые не пересекаются с $A$: $$ \text{Bel}(\bar{A}) = \sum_{S\,\mid\,S\cap A = \varnothing} m(S). $$

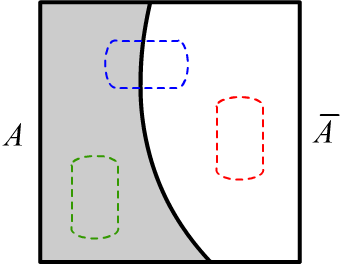Множество $2^\mathbb{H}$ разбивается на три части: все подмножества $A$ (на рисунке - зелёный цвет): $\{S\,\mid\, S\subseteq A\}$; все подмножества его отрицания $\bar{A}$ (красный цвет): $\{S\,\mid\, S\subseteq \bar{A}\}$; и все подмножества, которые пересекаются и с $A$, и c $\bar{A}$ (синий): $\{S\,\mid\,S\cap A\neq\varnothing \,\&\,S\cap \bar{A}\neq\varnothing \,\}$. Сумма их масс (как масса всего $2^\mathbb{H}$) равна единице. Поэтому правдоподобие (degree of plausibility), равное единице, уменьшенной на доверие истинности отрицания $A$ можно записать следующим образом: $$ \text{Pl}(A) ~=~ 1-\text{Bel}(\bar{A}) ~=~\sum_{S\,\mid\, S \cap A \neq \varnothing}m(S), $$ где сумма идёт по "синим" и "зелённым" подмножествам, а $\text{Bel}(\bar{A})$ - это суммарная масса "красных".

Так как в $\text{Bel}(A)$ и $\text{Bel}(\bar{A})$ не попадают "синие" подмножества, массы которых в общем случае отличны от нуля, приходим к выводу, что сумма доверия утверждения и его отрицания не превышает единицы: $$ \text{Bel}(A)+\text{Bel}(\bar{A}) \le 1. $$ Собственно именно это и требуется для любого утверждения. К примеру для примера с тремя гипотезами из предыдущего раздела, если $A=\{H_2\}$, тогда $\text{Bel}(\bar{A})=\text{Bel}(H_1,H_3)$ и $\text{Bel}(A)+\text{Bel}(\bar{A}) = 0.5$.

◊ Вычислим в примере с тремя гипотезами значения доверия некоторых множеств: $$ \begin{array}{lcll} \text{Pl}(H_1) &=& m(H_1)+m(H_1,H_2)+m(H_1,H_3)+m(H_1,H_2,H_3) = 0.3,\\ \text{Pl}(H_1,H_2) &=& m(H_1) + m(H_2) + m(H_1,H_2) + m(H_1,H_3)+ m(H_2,H_3)+ m(H_1,H_2,H_3) = 1, \\ \text{Pl}(H_1,H_3) &=& m(H_1) + m(H_3) + m(H_1,H_2)+ m(H_1,H_3)+ m(H_2,H_3)+ m(H_1,H_2,H_3) = 0.6, \\ \text{Pl}(H_1,H_2,H_3) &=& 1. \end{array} $$

Вероятность $P(A)$ истинности утверждения $A$ находится в интервале: $ m(A)~\le~\text{Bel}(A)~\le~P(A)~\le~ \text{Pl}(A). $

Правило Демпстера

Часто информация о поддержке (массе) подмножеств поступает из различных независимых источников и может быть противоречивой. Правило Демпстера согласует между собой такую информацию. Пусть есть два набора масс $m_1(S)$ и $m_2(S)$ для всех $S\subseteq \mathbb{H}$. В единую систему масс они объединяются следующим образом: $$ m(A) = \frac{1}{\mathcal{N}}\,\sum_{S_1\cap S_2=A} m_1(S_1)\cdot m_2(S_2). $$ Выше перебираются все пары подмножеств $S_1,S_2 \subseteq \mathbb{H}$, пересечение которых даёт $A\neq\varnothing$. Объединенная масса $m(A)$ пропорциональна сумме произведений масс таких подмножеств. Это соотношение инспирировано обычной теорией вероятности, в которой вероятность совместного наступления независимых событий равна произведению их вероятностей.

Нормировочный коэффициент $\mathcal{N}$ вычисляется таким образом, чтобы сумма $m(A)$ по всем подмножествам $\mathbb{H}$ равнялась единице: $$ \mathcal{N} ~=~ \sum_{S\subseteq \mathbb{H}}\sum_{S_1\cap S_2=S} m_1(S_1)\cdot m_2(S_2) ~=~ \sum_{S_1\cap S_2\neq \varnothing} m_1(S_1)\cdot m_2(S_2). $$ Наборы масс $m_1$, $m_2$ предполагаются нормированными на единицу, поэтому: $$ 1 = \sum_{S_1\subseteq \mathbb{H}}m_1(S_1) ~\sum_{S_2\subseteq \mathbb{H}}m_2(S_2) = \sum_{S_1,S_2\subseteq \mathbb{H}} m_1(S_1)m_2(S_2) = \sum_{S_1\cap S_2\neq \varnothing} m_1(S_1)\cdot m_2(S_2) ~~+ \sum_{S_1\cap S_2 = \varnothing} m_1(S_1)\cdot m_2(S_2), $$ где в последнем равенстве все пары подмножеств $(S_1,S_2)$ разбиты на пересекающиеся и непересекающиеся. В результате нормировочный коэффициент можно записать в более удобном для практических вычислений виде: $$ \mathcal{N} ~=~ 1~~-\sum_{S_1\cap S_2 = \varnothing} m_1(S_1)\cdot m_2(S_2). $$ Величина $\mathcal{N}$ является мерой конфликта наборов $m_1(S)$ и $m_2(S)$, так как суммирует все непересекающиеся подмножества $S_1\cap S_2=\varnothing$, которые тем не менее в каждом наборе получили ненулевые массы (есть "голоса" в их пользу).

Поиск преступника

Рассмотрим пример, позаимствованный из Yager, Liu (2008). Пусть есть трое подозреваемых в ограблении банка: Тони ($T$), Смит ($S$) и Дик ($D$). Пожилая свидетельница миссис Джонсон видела высокого человека возле банка в момент ограбления. Зрение у неё не очень хорошее, поэтому будем считать достоверность её показаний как $60\%$. Так как высокий рост имеют Тони и Дик, то $m_1(T,\,D) = 0.6$. В тоже время, других преступников в городе нет, миссис Джонсон больше ничего не видела, поэтому $m_1(T,\,S,\,D) = 0.4$.

Другой набор свидетельств основан на видеонаблюдении. Хотя преступник был в маске, камера зафиксировала нечеткое изображение его глаз, которые в $4$ раза чаще были черными, чем серыми. Так как у Смита черные глаза, считаем, что $m_2(S)=0.8$ и $m_2 (T,\,D) = 0.2$.

$$ m(S) = \frac{1}{\mathcal{N}}\,m_1(T,\,S,\,D)\,m_2(S)=\frac{0.32}{\mathcal{N}},~~~~~~~~~\mathcal{N}=1-m_1(T,\,D)\,m_2(S)=1-0.48~~~~~~\Rightarrow~~~~~m(S)=0.62. $$ Аналогично: $$ m(T,D) = \frac{0.12+0.08}{1-0.48}=0.38. $$

Приведём интервалы виновности подозреваемых отдельно по каждому источнику свидетельств и их объединение: $$ \begin{array}{ccccc} ~ & \text{миссис Джонсон} & \text{видеонаблюдение} & \text{объединение} \\ \hline T & [0.0,\,1.0] & [0.0,\,0.2] & [0.00,\,0.62] \\ S & [0.0,\,0.4] & [0.8,\,0.8] & [0.62,\,0.62] \\ D & [0.0,\,1.0] & [0.0,\,0.2] & [0.00,\,0.62] \end{array} $$

Отметим, что правило Демпстера в сильно конфликтующих ситуациях может приводить к странным результатам. Пусть, например, есть три подозреваемых $Т,D,S$ и два свидетеля $W_1$ и $W_2$, которые высказывают следующие суждения: $$ \begin{array}{lll} W1:& m(T)=0.9 & m(D)=0.1\\ W2:& m(S)=0.9 & m(D)=0.1\\ \end{array} $$ Применение правила Демпстера даёт $\mathcal{N}=0.99$ и $m(D)=1$, хотя оба свидетеля приписали гипотезе $m(D)$ малые массы.

Алгоритм классификации

В работе Chena et.,al. (2014) был предложен алгоритм классификации, построенный на основе правила Демпстера. В качестве фрейма различений $\mathbb{H}$ берутся гипотезы $H_k$ о принадлежности объекта к $k$-тому классу.

В простейшем случае двух классов $\mathbb{H}=\{H_1,H_2\}$ алгоритм работает следующим образом. Для каждого признака (по отдельности) строятся массовые функции в виде сигмоид $m_i(H_1)=1/(1+e^{v_i-t_i})$, $m(H_2)=1-m(H_1)$, где $v_i$ - значение $i$-того признака, а $t_i$ - порог (параметр обучения). Затем массовые функции параметров перемножаются (правило Демпстера) и нормируются. Полученная массовая функция используется в качестве классификатора: если $m(H_1) \gt m(H_2)$, то выбираем класс $H_1$.

Существует реализация этого алгоритма на Python.

Литература