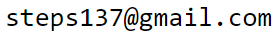ML: Интервальная логика
Введение
При рассмотрении вероятностной и нечёткой логик мы видели, что при логическом выводе для истинности высказывания или предиката может получаться не фиксированное значение, а некоторое ограничение в виде неравенства. Поэтому, в общем случае, истинность $A$ лучше характеризовать не одним вещественным числом, a парой чисел $[a_0,a_1]$. В этом документе мы рассмотрим вариант такой нечёткой логики.
Вероятностные и нечёткие истинности
Напомним, что следует различать два типа логических утверждений. Первый тип называется вероятностным. Такие утверждения относятся к будущим событиям или уже свершившимся событиям, детали которых не известны (и следовательно неизвестна их истинность): "Монета упадёт гербом вверх", "Графа убил дворецкий", "В закрытом ящике находится кот".
Второй тип истинности традиционно называется нечётким. Такие утверждения, основаны на степени принадлежности к нечётким множествам. Они носят сравнительный, относительный характер: $B$: "Маша красивая", $H$: "Кофе горячий". Если $B=0.7$, это означает, что "Маша красавица, но бывают красавицы и красивее".
Для вероятностной логики характерно выполнение закона исключения третьего (событие или происходит, или нет и третьего не дано). В нечёткой логике этот закон, обычно, не выполняется.
Иногда грань между этими двумя типами утверждений достаточно тонкая. Так, $I$: "карандаш находится в пенале" может рассматриваться в вероятностном смысле. (так, $I=1$, если он там действительно находится). Однако, это утверждение может иметь нечёткую истинность, если карандаш выглядывает из пенала. Если он выглядывает немного, то к примеру $I=0.9$, а если почти полностью высунут, то $I=0.1$. В общем случае эти типы истинности могут быть совмещены (вероятность того, что карандаш немного выглядывает).
Ниже мы будем рассматривать второй тип истинности.
Интервальная истинность
Истинность высказывания или предиката будем характеризовать парой чисел $[a_0,\,a_1]$. Будем считать, что $a_0$ равно степени уверенности в ложности высказывания $A$, а $a_1$ - уверенности в истинности. Это означает, что есть аргументы суммарной "силы" $a_1$, что $A$ истинно и доводы "силы" $a_0$, что оно ложно. Всегда $a_0+a_1 \le 1$. Случай равенства означает полностью определённую ситуацию: $a_1 = 1-a_0= T_A$, совпадающую с рассмотренной ранее нечёткой логикой. В этом случае $T_A$ - это обычная (в смысле нечёткой логики) степень истинности.
Абсолютно истинное высказывание равно $\mathbb{T}=[0,\,1]$, а полностью ложное - $\mathbb{F}=[1,\,0]$. Когда $\mathbb{U}=[0,\,0]$ ситуация полностью не определена (высказывание может быть как истинным, так и ложным и нам не известно это значение). Мера неопределённости $1-a_0-a_1$ максимальна и равна $1$ для полностью неопределённого утверждения и минимальна ($0$) для полностью определённого.
Например, мы не знаем на сколько сильно карандаш выглядывает из пенала (и находится ли он там). Тогда истинность утверждения "Карандаш в пенале" будет равна $[0,\,0]$.
На самом деле, обычно, истинность большинства утверждений будет определённой. Однако в процессе логического вывода может появляться неопределённость, которая может уменьшаться по мере поступления новой информации.
Логические связки
Отрицание интервальной истинности переставляет местами значения $a_0$ и $a_1$: $$ A=[a_0,\,a_1],~~~~~~~~~~~\neg A = [a_1,\,a_0]. $$ Это означает, что, если мы имели степень уверенности $a_1$ в истинности $A$, то с такой же степени уверенности считаем, что $\neg A$ ложно. Логические связки для интервальных истинностей определим следующим образом: $$ \begin{array}{lclcl} [a_0\,a_1] & \,\&\, & [b_0\,b_1] &~~~=~~~& \bigr[\max(a_0,b_0),~\min(a_0,b_0)\bigr]\\ [a_0\,a_1] & \vee & [b_0\,b_1] &~~~=~~~& \bigr[\min(a_0,b_0),~\max(a_0,b_0)\bigr]\\ \end{array} $$ Несложно видеть, что введенные операции сохраняют свойство $0 \le a_0+a_1 \le 1$ и для составных высказываний.
Интервальные логические И,ИЛИ, как и в булевой алгебре симметричны, ассоциативны и дистрибутивны.
Для них выполняются правила де-Моргана и двойного отрицания:
$$
\neg(A\,\&\,B) = \neg A\vee \neg B,~~~~~~~~~~~\neg(A\vee B) = \neg A\,\&\, \neg B,~~~~~~~~~~~~\neg(\neg A) = A.
$$
Кроме этого справедливы законы поглощения:
$$
A\vee A=A,~~~~~~A\,\&\,A = A,~~~~~~~A\vee (A\,\&\,B)=A,~~~~~~~A\,\&\, (A\vee B)=A.
$$
Однако, нарушаются законы исключения третьего:
$$
\begin{array}{llll}
A\vee \neg A = \bigr[\min(a_0,a_1),\,\max(a_0,\,a_1)\bigr] ~~~~\neq~~~ \mathbb{T}=[0,1].\\
A\,\&\, \neg A = \bigr[\max(a_0,a_1),\,\min(a_0,\,a_1)\bigr] ~~~~\neq~~~ \mathbb{F}=[1,0],
\end{array}
$$
что типично для многозначных логик. Чем мера истинности $a_1$ или ложности $a_0$ ближе к единице
(почти истинное или почти ложное утверждение), тем "лучше выполняются" законы исключения третьего.
Таблицы истинности
Для достоверно ложного $\mathbb{F}=[1,\,0]$ и достоверно истинного $\mathbb{T}=[0,\,1]$ высказываний и произвольного высказывания $A=[a_0,\,a_1]$ имеем: $$ \mathbb{F}\,\&\, A = \mathbb{F},~~~~~~~~~~~\mathbb{T}\,\&\,A = A,~~~~~~~~~~~\mathbb{F}\vee A = A,~~~~~~~~~~~\mathbb{T}\vee A = \mathbb{T}. $$ Неопределённое высказывание $\mathbb{U}=[0,0]$ c $\neg \mathbb{U}= \mathbb{U}$ добавляет к ним: $$ \mathbb{U}\,\&\, \mathbb{F} = \mathbb{F},~~~~~~~~~~~\mathbb{U}\,\&\,\mathbb{T} = \mathbb{U},~~~~~~~~~~~ \mathbb{U}\vee \mathbb{F} = \mathbb{U},~~~~~~~~~~~\mathbb{U}\vee \mathbb{T} = \mathbb{T}, $$ что эквивалентно таблицам истинности в трёхзначной логике Лукасевича.Приведём интерпретацию этой таблицы, если ограничиться только трёхзначнной логикой. Неопределённое высказывание $\mathbb{U}$ может оказаться как истинным, так и ложным, но нам "пока" неизвестно это значение. Поэтому, например $\mathbb{U}\vee \mathbb{F}$ будет истинным, если $\mathbb{U}$ истинным и ложным, если $\mathbb{U}$ окажется ложным. Поэтому результат операции не определён: $\mathbb{U}$. В тоже время $\mathbb{U}\vee \mathbb{T}$ будет истинным, в не зависимости от того, каким окажется $\mathbb{U}$.
Отметим проекционные свойства для произвольного высказывания $A=[a_0,\,a_1]$: $$ \mathbb{U}\,\&\, A = [a_0,\,0],~~~~~~~~~~~\mathbb{U}\vee A = [0,\,a_1]. $$
Геометрическое представление
Так как истинность высказываний определяется двумя числами, их можно изобразить точками на плоскости внутри треугольника с вершинами $\mathbb{F},\,\mathbb{U},\,\mathbb{T}$: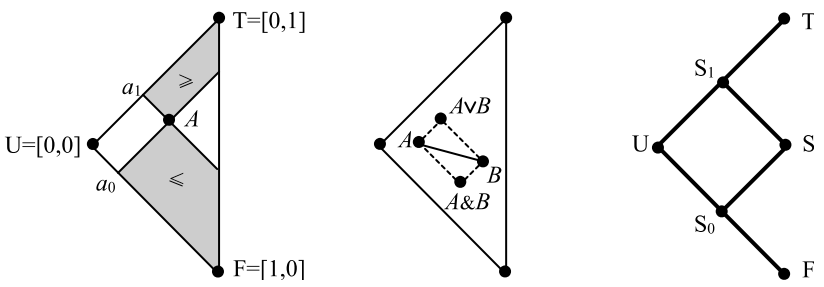
По оси $\mathbb{U}-\mathbb{F}$ откладывается значение $a_0$, а по оси $\mathbb{U}-\mathbb{T}$ значение $a_1$ (выше первый рисунок). На линии $\mathbb{F}-\mathbb{T}$ находятся полностью определённые вероятности для которых $a_0+a_1=1$.
Если отрезок $A-B$ между двумя высказываниями образует меньший угол с осью $\mathbb{U}-\mathbb{F}$, то геометрически точки дизъюнкции (ИЛИ) и коньюнкции (И) находятся в вершинах прямоугольника, как это изображено на втором рисунке. Если же у отрезка $A-B$ меньше угол с осью $\mathbb{U}-\mathbb{T}$, то $A\vee B$ равно тому высказыванию, который на диаграмме находится выше, а $A\,\&\, B$, тому который ниже.
На множестве высказываний можно ввести частичный порядок при помощи следующего определения: $$ A\leq B ~:~~~ (a_0 \geq b_0)\,\&\,(a_1 \leq b_1). $$ Выше на первом рисунке в верхней заштрихованной области находятся все высказывания большие $A$, а в нижней области -- все высказывания меньшие $A$.
Так как порядок имеет верхнюю $\mathbb{T}$ и нижнюю $\mathbb{F}$ границы, он образует дистрибутивную решётку. В качестве примера, такая решётка представлена на третьем рисунке для шести высказываний, где $S=[1/2,1/2]$, $S_1=[1/2,0]$, $S_1=[0,1/2]$. Напомним, что на подобных диаграммах если, двигаясь от узла $B$ вверх по рёбрам можно попасть в узел $A$, то $A\geq B$, а $B \leq A$. Если такого пути нет, то узлы не связаны порядком (выше таковы $\mathbb{U}$ и $\mathbb{S}$). Рёбра рисуются минимальным образом (если существует такой $X$, что $A\leq X\leq B$, то между $A$ и $B$ ребро не проводится).