ML: N-граммы
Введение
Этот документ является продолжением обсуждения вероятностных методов в машинном обучении. Мы рассмотрим классический и не утративший своего значения метод n-грамм для прогнозирования последовательностей. В качестве примера таких последовательностей будут рассмотрены буквы и слова текстов на ествественном языке. Однако, этот же подход с небольшими модификациями можно использовать при анализе временных рядов и в других задачах.
Приведенные далее примеры на Python используют библиотеку nltk (Natural Language Toolkit) и могут быть найдены в файле ML_NGrams.ipynb. Рассмотрен также существенно более быстрый модуль my_ngrams.py, основанный на древесном представлении n-грамм.
nltk: Словарь
Пусть произведена токенизация последовательности (она разбита на элементарные символы). В качестве токенов могут выступать буквы, слова естественного языка или номера интервалов изменения вещественной величины (при анализе временных рядов). Чтобы создать словарь всех возможных токенов, в nltk их список text передаётся экземпляру класса Vocabulary:
from nltk.lm import Vocabulary text = ['a', 'b', 'r', 'a', 'c', 'a', 'd', 'a', 'b', 'r', 'a'] vocab = Vocabulary(text, unk_cutoff=2)Класс Vocabulary является надстройкой над стандартным классом Counter(), экземпляр которого находится в vocab.counts. Он составляет частотный словарь. Параметр unk_cutoff задаёт порог для редких слов. Если слово в списке встречается менее unk_cutoff раз, то оно заменяется на служебное слово '<UNK>' (неизвестное).
Словарь помнит все токены (vocab[t] возвращает число появлений токена t в списке).
При этом конструкция
t in vocab возвращает True только для токенов
с частотой выше или равных порогу unk_cutoff:
print(vocab['a'], 'a' in vocab) # 5 True встретился 5 раз, попал в словарь print(vocab['c'], 'c' in vocab) # 1 False не попал в словарь (1 < unk_cutoff=2) print(vocab['Z'], 'Z' in vocab) # 0 False такого вообще не былоТекст для словаря можно добавлять произвольное число раз:
vocab.update(['c', 'c']) # добавили слов print(vocab['c'], 'c' in vocab) # 3 True превосходит порог cutoffИнформацию о словаре, список слов (включая <UNK>) и список токенов без учёта порога, можно получить следующим образом:
print(vocab) # Vocabulary cutoff=2 unk_label='<UNK>' and 5 items
len(vocab) # 5 число слов включая токен '<UNK>'
sorted(vocab) # ['<UNK>', 'a', 'b', 'c', 'r'] что считает словарём
sorted(vocab.counts) # ['a', 'b', 'c', 'd', 'r'] всё, что получил
[ (v, vocab[v]) for v in vocab] # [('a',5), ('b',2), ('r',2), ('c',3), ('<UNK>',2)]
При помощи метода lookup в любом списке (включая вложенные списки)
можно проверить слова на наличие их в словаре и незнакомые (или редкие) заменить на '<UNK>'
vocab.lookup('a') # 'a'
vocab.lookup(['a', 'aliens']) # ('a', '<UNK>')
vocab.lookup(['a', 'b', ['Z', 'b']]) # ('a', 'b', ('<UNK>', 'b'))
nltk: N-граммы
Последовательность n токенов в тексте называется n-граммой. В nltk функция ngrams возвращает генератор на список всех n-грамм. Для случая n=2 служит функция bigrams. Так, для списка целых чисел [1...5] получим все 3-граммы и 2-граммы:
from nltk.util import ngrams, bigrams list( ngrams ([1,2,3,4,5], 3) ) # [(1, 2, 3), (2, 3, 4), (3, 4, 5)] list( bigrams([1,2,3,4,5]) ) # [(1, 2), (2, 3), (3, 4), (4, 5)]Подчеркнём, что функции воозвращают генераторы. Поэтому, если написать bg = bigrams([1,2,3,4,5]), а потом дважды вызвать list(bg), то второй вызов вернёт пустой список (генератор отработает в первом вызове).
При обработке естественного языка, тексты разбиваются на предложения. В nltk принято окружать предложения токенами <s> ...</s>. Для выполнения этой процедуры существует набор функций препроцессинга. Они также возвращают генераторы, поэтому являются "одноразовыми":
from nltk.lm.preprocessing import pad_both_ends, padded_everygram_pipeline list( pad_both_ends(['a','b'], n=2) ) ) # ['<s>', 'a', 'b', '</s>'] list( pad_both_ends(['a','b'], n=3) ) ) # ['<s>', '<s>', 'a', 'b', '</s>', '</s>']Параметр n указывает для каких n-грамм "требуется" такая "забивка":
list( bigrams( pad_both_ends(['a','b'], n=2) ) ) # [('<s>','a'), ('a','b'), ('b','</s>')]
Использовать значение n > 2 или вообще отказаться от падинга (n=1) зависит от конкретной задачи.
При помощи функции padded_everygram_pipeline можно подготовить список предложений для работы с n-граммами:
sents = [['a', 'b'], ['b', 'a'] ] # 2 "предложения" train, vocab = padded_everygram_pipeline(2, sents) print( list(vocab) ) # ['<s>', 'a', 'b', '</s>', '<s>', 'b', 'a', '</s>']В зависимости от задачи, "предложения" могут быть как реальными предложениями текста, так и отдельными документами. Следует помнить, что при вычислении условных вероятностй (см. ниже) n-граммы будут составляться внутри каждого "предложения" без их пересечения между "предложениями".
Смысл использования забивок состоит в возможности получения вероятности первого, второго и т.д. слова в предложении. Например для триграмм, если "<s> <s> мама мыла раму </s> </s>", то вероятность первого слова равна P(<s> <s> => мама).
Отметим также, что, как и ранее, padded_everygram_pipeline возвращает "одноразовые" генераторы, поэтому на практике они сразу передаются в следующее звено обработки текста. Кроме этого, первый аргумент padded_everygram_pipeline должен, не зависимо от паддинга, быть равен числу n-грамм, иначе будет получен неверный генератор train.
nltk: Условные вероятности
Напомним, что вероятностная языковая модель для данного слова $w$, по его контексту $\{\mathcal{T} - w\}$ (текст $\mathcal{T}$ без слова $w$) предсказывает вероятность этого слова: $P(w|\mathcal{T} - w)$. Обычно, в качестве контекста используются идущие перед $w$ слова. Если известна условная вероятность $ P( w_n\,|\, w_1...w_{n-1})\equiv P(w_1...w_{n-1}\Rightarrow w_n)$ того, что после цепочки слов (токенов) $w_1...w_{n-1}$ идёт слово $w_n$, то выбрав наибольшую вероятность, можно предсказать это слово. Оценка таких условных вероятностей проводится при помощи частотного анализа появления в тексте n-грамм $(w_1,...,w_{n})$.
Соответствующие подсчёты в nltk производятся семейством языковых моделей. Рассмотрим сначала класс MLE (Maximum Likelihood Estimator):
from nltk.lm import MLE sents = [['a','b','c'], ['b', 'a'] ] # 2 "предложения" train, vocab = padded_everygram_pipeline(n, sents) n = 2 lm = MLE(n) # работаем с биграммами lm.fit(train, vocab) # обучаемся (считаем вероятности)Генератор vocab содержит весь текст с объединёнными предложениями (окруженные символами <s>, </s>). Он используется для составления словаря. В train находится генераторы n-грамм для каждого предложения. Составление n-грамм производится отдельно для каждого предложения. Поэтому, независимо от наличия забивок <s>, </s>, n-граммы для 1,2,...,n между предложениями не пересекаются.
Так как для больших текстов функция fit работает достаточно медленно, желательно выводить процесс её работы. Например, пусть есть одно предложение из списка слов: words и нас интересуют вероятности n-грамм (для n=1,...,n). Тогда модель можно обучить следующим образом:
lm = MLE(n)
lm.fit( [ ngrams(words,1) ], words) # юниграммы и словарь
for i in range(2, n+1):
lm.fit( [ ngrams(words, i) ] ) # следующие n-граммы
print(f"n:{i:2d}> ngrams:{lm.counts.N():10d}")
После обучения (метод fit) можно вывести число запомненных n-грамм и словарь (предыдущий пример):
print(lm.counts.N()) # 16 число n-грамм, n=1,2 print(sorted(lm.vocab) ) # ['</s>', '<UNK>', '<s>', 'a', 'b', 'c']Число появлений в тексте и вероятность одиночного символа возвращает объект counts и метод score:
print(lm.counts['a'], lm.score('a')) # 2 0.222 = 2/9 (с учётом символов '</s>''<s>')
Число 2-грамм и условную вероятность P(a => b)
получаем так:
print(lm.counts[['a']]['b'], lm.score('b', ['a'])) # 1 0.5
Действительно, в тексте есть две биграммы, начинающихся с 'a':
('a','b') и ('a','</s>'), где вторая - в конце второго предложения.
Поэтому P(a => b) = 1/2.
В общем случае, если contex=$[w_1,...,w_{n-1}]$,
то число n-грамм равно lm.counts[context][$w_n$],
а условная вероятность $P(w_1...w_{n-1}\Rightarrow w_n)$ равна
lm.score($w_n$, context).
nltk: Энтропия и перплексия
Зная условные вероятности, можно вычислить перплексию тестового текста, который необходимо предварительно разбить на n-граммы:
test = [('a', 'b'), ('b', 'a'), ('a', 'b')]
print("e=", lm.entropy(test) ) # 1.0
print("p=", lm.perplexity(test), 2**lm.entropy(test) ) # 2.0 2.0
print( [ lm.score(b[-1], b[:-1] ) for b in test] ) # [0.5, 0.5, 0.5]
Энтропия $H$ (с логарифмом по основанию 2), а затем перплексия $\mathcal=2^H$
вычисляется следующим образом:
sum( [ -lm.logscore(ng[-1], ng[:-1]) for ng in test] )/len(test)где lm.logscore равен двоичному логарифму от lm.score.
Проблемы больших словарей
Если в в марковских моделях языка, качестве элементарных символов выступают слова, то размер словаря становится очень большим. Это приводит к следующим проблемам:
- Словарь естественного языка открыт и при тестировании модели могут появляться слова, которых не было в обучающем корпусе (проблема OOV - out of vocabulary).
- Число условных вероятностей достаточно быстро растёт и требует заметных затрат памяти.
Так, число уникальных (1...10)-грамм русских букв на тексте длиной 6'678'346
букв равно:
[33, 898, 10'651, 68'794, 278'183, 794'837, 1'633'700, 2'609'627, 3'540'927, 4'338'087].
Чем длиннее обучающий текст, тем больше потребуется памяти. - Большинство слов в словаре имеют малую вероятность (закон Ципфа) и для вычисления условных вероятностей с их участием, необходимы очень большие корпусы текстов. В любом случае, некоторые n-граммы, из тестовом корпусе окажутся отсутствующими в тренировочном. Соответствующие им условные вероятности будут равны нулю.
С проблемой OOV можно бороться следующим образом. Редкие слова в обучающем корпусе сразу заменяются на одно слово UNK (unknown). Соответственно, условные вероятности будут содержать это служебное слово и более или менее справляться с незнакомыми словами (также заменяемыми на UNK) при тестировании модели. Приведём пример:
sents = [['a', 'b', 'c'], ['b', 'a'] ] # 2 "предложения"
vocab = Vocabulary(unk_cutoff=2)
for s in sents:
vocab.update(s)
sents = vocab.lookup(sents) # (('a', 'b', '<UNK>'), ('b', 'a'))
train, vocab = padded_everygram_pipeline(2, sents)
lm = MLE(2)
lm.fit(train, vocab)
print( lm.score('<UNK>')) # 0.11111 = 1/9
print( lm.score('<UNK>', ['b'] ) ) # 0.5 = P(b => <UNK>)
Появление нулевых вероятностей, не позволяющих вычислить энтропию и перплексию,
рассмотрим на следующем тренировочном корпусе:
('a', 'b', 'c', 'b', 'a').
Биграммы ('a','c') в этом корпусе нет.
Если считать, что P('a' => 'c') = 0, то при тестировании получим нулевую
вероятность и бесконечные энтропию и преплексию:
test = [('a', 'b'), ('a', 'c')]
print(lm.score('c', ['a'])) # 0.0 P( a => c)
print(lm.entropy(test) ) # inf
Вообще, если оценивать условную вероятность по формуле:
$$
P(w_1...w_{n-1}\Rightarrow w_n) = \frac{N(w_1...w_n)}{N(w_1...w_{n-1})},
$$
то для длинных n-грамм нулю может равняться, как числитель $N(w_1...w_n)$,
так и знаменатель $N(w_1...w_{n-1})$.
Кроме этого, при малых значениях $N(w_1...w_{n-1})$ оценка эмпирической условной
вероятность становится очень ненадёжной.
Сглаживание, откат и интерполяция
Проблему нулевых условных вероятностей можно решать различными способами. Самый простой и грубый - это сделать нулевые вероятности маленькими, но ненулевыми. Для этого используют сглаживание Lidstone, частный случай которого ($\gamma=1$) называется сглаживанием Лапласа $$ \tilde{P}(w_1,...,w_{n-1}\Rightarrow w_n) = \frac{ N(w_1...w_n) + \gamma}{N(w_1...w_{n-1})+|\mathcal{V}|\cdot\gamma}, $$ где $N(...)$ - число появления последовательностей слов в тексте, а $+|\mathcal{V}|$ - число слов в словаре. Несложно видеть, что сумма $\tilde{P}$ по всем $w_n\in \mathcal{V}$ равна единице. Заметим, что, если в обучающем корпусе нет n-граммы $(w_1...w_{n-1})$, то вероятности всех слов словаря будет равна $1/|\mathcal{V}|$.
Другой способ - это откат (backoff). Так, если, например, $P(w_1,w_2 \Rightarrow w_3)$ равна нулю (3-грамма $w_1w_2w_3$ не встретилась в обучающем корпусе), то берут вероятность $P(w_2 \Rightarrow w_3)$. Если и она равна нулю, то просто $P(w_3)$. Такой метод требует дополнительной нормировки, т.к. сумма получающихся вероятностей по всем словам словаря, вообще говоря, не равна 1. Соответственно, перплексия будет вычислена неверно. Существуют различные вариации backoff-стратегии устраняющие эту проблему.
Достаточно простой способ борьбы с нулевыми вероятностями - это интерполяция, при помощи которой условную вероятность вычисляют следущим образом: $$ \tilde{P}(w_1...w_{n-1}\Rightarrow w_n) = \frac{ P(w_1...w_n\Rightarrow w) +\lambda_1\, P(w_2...w_{n-1}\Rightarrow w) +... + \lambda_n\,P(w) } { 1+\lambda_1+...+\lambda_n }. $$ Коэффициенты $\lambda_1,...\lambda_n$ должны убывать (больший вес дают более "длинные" условные вероятности). Однако, если они равны нулю, информация о вероятности символа $w_n$ будет получена из более короткой условной вероятности и $\tilde{P}$ никогда не будет нулевой. Например, можно выбрать $\lambda_k=\beta^k$, где $\beta \in [0...1]$ - параметр модели. Формально, сумма этого выражения по всем $w$ из словаря равна единице (благодаря знаменателю). Однако, это будет так, только, если $P(w_{n-k}...w_{n-1} \Rightarrow w_n)$ отлично от нуля хотя бы для одного $w_n$. Поэтому, и в числителе, и в знаменателе следует убирать первые слагаемые для $P(w_{1}...w_{k} \Rightarrow w)$ у которых $N(w_{1}...w_{k})=0$ (т.е. $P=0$ для всех слов словаря).
Можно также ликвидировать слагаемые с малым значение $N(w_{1}...w_{k})$ (т.к. они дают ненадёжное значение вероятности) или учитывать в весах ошибку измерения вероятности.
nltk: Языковые модели
Методы борьбы с нулевыми условными вероятностями реализованы в nltk как различные языковые модели. Они имеют однотипный интерфейс, но различные алгоритмы вычисления функции score. Рассмотренная выше модель MLE для условной вероятности просто возвращает N(w_1...w_n)/N(w_1...w_{n-1}) Другие модели имеют следующие названия:
- nltk.lm.Laplace - Laplace (add one) smoothing
- nltk.lm.Lidstone - Lidstone-smoothed scores
- nltk.lm.KneserNeyInterpolated - Kneser-Ney smoothing
- nltk.lm.WittenBellInterpolated - Witten-Bell smoothing
class Interpolated(LanguageModel):
def __init__(self, beta, *args, **kwargs):
super().__init__(*args, **kwargs)
self.beta = beta
def unmasked_score(self, word, context=None):
if not context:
counts = self.context_counts(context)
return counts[word] / counts.N() if counts.N() > 0 else 0
prob, norm, coef = 0, 0, 1;
for i in range(len(context)+1):
counts = self.context_counts(context[i:])
if counts.N() > 0:
prob += coef * ( counts[word] / counts.N() )
norm += coef
coef *= self.beta
return prob/norm
Метод unmasked_score вызывается в методе score
после замены незнакомых токенов на <UNK> (при помощи функции lookup).
Приведём примеры вычисления биграмных условных вероятностей и их суммы при помощи различных
методов:
MLE(2) [0.0, 0.0, 0.5, 0.0, 0.5 ] 1.0 Laplace(2) [0.125, 0.125, 0.25, 0.125, 0.25 ] 0.875 Lidstone(0.5, 2) [0.1, 0.1, 0.3, 0.1, 0.3 ] 0.900 KneserNey(2) [0.016, 0.016, 0.466, 0.016, 0.466] 0.983 WittenBell(2) [0.049, 0.049, 0.438, 0.024, 0.438] 1.0 Smooth(0.5, 2) [0.074, 0.074, 0.407, 0.037, 0.407] 1.0 Backoff(2) [0.222, 0.222, 0.5, 0.111, 0.5 ] 1.555Обратим внимание, на последнюю строчку в которой представлен результат наивного отката backoff, который приводит к завышенным вероятностям, сумма которых больше единицы.
nltk: Генерация текста
Данную языковую модель можно использовать для генерации текста. Для этого служит метод generate, который может начать генерацию с случайного слова или затравочного текста text_seed (списка начальных слов):lm.generate(5, random_seed=3) # ['<s>', 'b', 'a', 'b', 'c'] lm.generate(4, text_seed=['<s>'], random_seed=3) # ['a', 'b', 'a', 'b']
Метод generate для получения очередного слова берёт список text_seed (или накопившийся при генерации текст), отрезает от него последние (n = lm.order) - 1 символов (контекст). Затем ищет слова, которые в тестовой последовательности могли следовать за этим контекстом. Если таких слов нет, контекст укорачиваться. Вероятности таких слов далее вычисляются "честно" в рамках данной языковой модели.
Статистические свойства русского языка
Рассмотрим 33 буквы в текстах русского языка с алфавитом: "_абвгдежзийклмнопрстуфхцчшщъыьэюя", переводя текст в нижний регистр, заменяя 'ё' на 'e' и "не алфавитные" символы на пробелы (подчёркивание _ - это пробел). Затем устраним несколько идущих подряд пробелов. Вероятности отдельных букв по тексту длины N=8'343'164 равны:
'_': 0.1641, 'с': 0.0437, 'у': 0.0238, 'б': 0.0143, 'э': 0.0030, 'о': 0.0948, 'л': 0.0407, 'п': 0.0234, 'ч': 0.0126, 'ц': 0.0030, 'е': 0.0701, 'р': 0.0371, 'я': 0.0182, 'й': 0.0093, 'щ': 0.0029, 'а': 0.0685, 'в': 0.0368, 'ь': 0.0159, 'ж': 0.0084, 'ф': 0.0017, 'и': 0.0554, 'к': 0.0290, 'ы': 0.0155, 'ш': 0.0071, 'ъ': 0.0003 'н': 0.0551, 'м': 0.0264, 'г': 0.0152, 'х': 0.0070, 'т': 0.0516, 'д': 0.0259, 'з': 0.0144, 'ю': 0.0049,
Перплексия $e^H$ русского текста по вероятностям одиночных букв равна: 20.7 ($\ln H=3.03$, $\log_2H = 4.37$).
Условные и совместные вероятности глубины два, отсортированные по убыванию условных вероятностей (первая цифра $P(\mathbf{э}\Rightarrow\mathbf{т})=0.83$, вторая - $P(\mathbf{э},\mathbf{т})=0.0025$):
эт,0.83, 0.0025 ще,0.52, 0.0015 ъя,0.41, 0.0001 ы_,0.29, 0.0045 пр,0.27, 0.0064 й_,0.79, 0.0074 го,0.50, 0.0076 по,0.40, 0.0093 м_,0.29, 0.0076 щи,0.27, 0.0008 я_,0.63, 0.0114 ъе,0.45, 0.0001 за,0.36, 0.0052 че,0.28, 0.0035 ко,0.27, 0.0078 ь_,0.62, 0.0098 х_,0.45, 0.0031 и_,0.32, 0.0176 ше,0.28, 0.0020 то,0.27, 0.0138 ю_,0.53, 0.0026 же,0.41, 0.0035 хо,0.30, 0.0021 у_,0.28, 0.0066 е_,0.26, 0.0180
Для 3-грамм аналогично, но с фильтром по совместным вероятностям $P(x_1,x_2,x_3) > 0.001$:
ые_, 0.98, 0.0011 ся_, 0.91, 0.0032 ее_, 0.84, 0.0011 их_, 0.79, 0.0012 ый_, 0.98, 0.0015 ий_, 0.89, 0.0011 ть_, 0.83, 0.0046 ия_, 0.78, 0.0011 лся, 0.97, 0.0014 я_, 0.86, 0.0022 ой_, 0.83, 0.0030 му_, 0.77, 0.0016 что, 0.95, 0.0030 эт, 0.85, 0.0024 его, 0.83, 0.0025 ие_, 0.75, 0.0016 сь_, 0.95, 0.0025 ая_, 0.84, 0.0017 это, 0.81, 0.0020 ей_, 0.71, 0.0014 ет_, 0.46, 0.0021Для 4-грамм с фильтром $P(x_1,x_2,x_3,x_4) > 0.0001$
огда, 1.00, 0.0006 рый_, 1.00, 0.0002 _ее_, 1.00, 0.0004 ные_, 1.00, 0.0006 оей_, 1.00, 0.0002 рые_, 1.00, 0.0002 _ей_, 1.00, 0.0001 ный_, 1.00, 0.0007 оего, 1.00, 0.0001 сех_, 1.00, 0.0001 ках_, 1.00, 0.0001 оих_, 1.00, 0.0001 _кто, 1.00, 0.0003 ных_, 1.00, 0.0004Перплексия достаточно быстро насыщается и перестаёт уменьшаться (len(text_trn)=6'678'346, len(text_tst)=1'664'818, методы см. в приложении и my_ngrams.py):
Laplas(1,order) Interpolated(beta, minN=1) Interpolated(beta, minN=3)
order 0.1 0.5 0.8 0.2 0.5 0.8
----------------------------------------------------------------------------------------
1 20.74 20.74 20.74 20.74 20.74 20.74 20.74
2 12.04 12.25 13.27 13.92 12.51 13.27 13.92
3 8.25 8.33 9.24 10.11 8.50 9.24 10.11
4 5.85 5.79 6.52 7.43 5.91 6.52 7.44
5 5.00 4.59 5.01 5.83 4.62 5.02 5.84
6 5.49 4.39 4.34 4.98 4.23 4.35 5.01
7 7.17 4.95 4.12 4.53 4.31 4.11 4.58
8 9.94 6.20 4.16 4.30 4.61 4.07 4.35
9 4.33 4.19 4.99 4.11 4.25
10 4.56 4.16 5.36 4.18 4.20
11 4.81 4.16 4.26 4.18
12 5.04 4.17 4.32 4.18
------------------------------------------------------------------------------------------
best 5.00 4.39 4.12 4.16 4.23 4.07 4.18
Генерация текста по затравочной фразе "три девицы под окном пряли поздно вечерко" (ниже повторяем "вечерко" и используем интерполяцию с $\beta=0.5$):
1 вечеркоелшыго сво гшо ддлтготуэут ттм уи е т ьгевокбт кы жслиотепяниэ дпжевткк нотго вдат на кытен ауьд 2 вечеркогогл ауек кинуге дис уко т номотме виешеызл пряь анй верилере альо овокалиср блччл фричридаелю 3 вечеркообойыхоложе жал с илсяузна эти сти тсково кахопнодто слыекеть наня мот сквексар ни о внылсяарус 4 вечеркокончистоотвалиамекам отается дерсталовом пе я назы и ги сел такогдая что полегкомордиямоглазавшна 5 вечерконечноговя потоненным что стало человам по как что мая тичесили глу приваннытные готовый фарее 6 вечерком состоинственно он не круглой не было и правительно бы чепухую зервы отдадоставая разбогат я 7 вечерком по возвращаясь ко торчащегося обратом городаряла креслу отправятся сказала анна мира а о с 8 вечерком спасибо комов ну и что на паука одуванчик способно расправах вот загременно перемену на часы 9 вечерком главная самое не будет но если согласится а помогать ими и очень и очень доволен и наобороны
- пробел, гласные, глухие, звонкие, ьъ, как насыщается преплексия
- разбитие слов на "слоги", минимизация энтропии
Для 28 английских букв _'abcdefghijklmnopqrstuvwxyz (плюс пробел и апостроф)
_ 0.1957, i 0.0498, u 0.0189, k 0.0100, e 0.1055, s 0.0486, m 0.0188, v 0.0072, t 0.0725, r 0.0451, g 0.0179, j 0.0025, a 0.0679, d 0.0415, y 0.0163, ' 0.0022, o 0.0592, l 0.0311, f 0.0157, x 0.0012, h 0.0533, w 0.0215, p 0.0140, z 0.0008, n 0.0501, c 0.0196, b 0.0124, q 0.0004перплексия равна 17.07. Для MarkovInterpolated(beta=0.5, minN = 3) при order = 9 перплексия снижается до 2.97 (c len(text_trn)=17'246'125 и len(text_tst)=4'696'973).
Уровень слов
Наиболее популярные слова в ipm (instances per million words для "корпуса" длиной 1'097'544 слов).
и: 40571 за: 4516 мы: 2458 теперь: 1542 раз: 1148 этом: 922 в: 23556 из: 4439 для: 2205 была: 1457 во: 1138 вам: 910 не: 23270 же: 3894 нет: 2193 ничего: 1453 тоже: 1115 всех: 910 что: 16062 она: 3835 уже: 2184 чем: 1446 один: 1098 тем: 892 на: 15092 сказал: 3828 ну: 2183 были: 1445 здесь: 1096 ей: 885 я: 13387 от: 3565 когда: 2023 того: 1442 том: 1083 сам: 885 он: 11503 еще: 3417 если: 1977 быть: 1433 после: 1070 которые: 872 с: 11490 мне: 3396 до: 1944 будет: 1419 потому: 1066 тогда: 872 то: 8884 бы: 3343 или: 1908 этого: 1416 тебе: 1061 про: 867 а: 8884 ты: 3277 него: 1828 тут: 1353 вас: 1055 больше: 867 как: 7987 меня: 3231 ни: 1776 время: 1316 со: 1050 сказала: 857 это: 7628 да: 3210 есть: 1776 где: 1305 чего: 1035 нам: 844 все: 6730 только: 3164 даже: 1720 себя: 1298 тебя: 1021 ним: 840 но: 6510 о: 3048 их: 1714 потом: 1297 дело: 1014 через: 836 его: 5999 был: 2874 там: 1709 ли: 1284 человек: 1009 спросил: 834 к: 5932 вот: 2717 кто: 1707 под: 1263 который: 993 тот: 817 по: 5455 вы: 2632 очень: 1698 себе: 1235 сейчас: 985 можно: 816 у: 4948 они: 2552 чтобы: 1690 нас: 1234 просто: 971 глаза: 796 так: 4815 ее: 2508 надо: 1599 этот: 1226 при: 951 нибудь: 785 было: 4580 ему: 2507 может: 1552 без: 1172 них: 939 знаю: 782
3-граммы, отсортированы по убыванию условной вероятности:
о том что, 0.54, 0.00030 по крайней мере, 0.99, 0.00010 в том что, 0.45, 0.00020 несмотря на то, 0.41, 0.00010 для того чтобы, 0.84, 0.00018 так и не, 0.22, 0.00009 на то что, 0.58, 0.00015 в конце концов, 0.62, 0.00009 в то время, 0.56, 0.00013 в первый раз, 0.80, 0.00009 я не знаю, 0.12, 0.00011 в это время, 0.57, 0.00009 так же как, 0.34, 0.00011 в самом деле, 0.59, 0.00009 на самом деле, 0.85, 0.00011 не может быть, 0.35, 0.00009 то время как, 0.70, 0.00010 после того как, 0.88, 0.00009 то что он, 0.11, 0.00010 до сих пор, 1.00, 0.00009
Если ограничится достаточно коротким корпусом длиной 1'097'544 слов и слова встречающиеся менее 10 раз заменить на <UNK>, то получится словарь в 10'598 слов. В этом случае, в отличии от букв, существенного уменьшения перплексии достичь нельзя. Так для MarkovInterpolated(beta=1, minN = 3) имеем:
order: 1 2 3 4 5 perplexity: 454.94 250.91 236.91 239.85 241.06Число уникальных n-грамм: [10'598, 331'262, 757'821, 990'097, 1'068'222] достаточно велико и для качественной работы марковской модели требуется существенно больший корпус текстов.
В национальном корпусе русского языка www.ruscorpora.ru длиной около 200 млн слов. Там же доступны для загрузки 2,3,4,5 - граммы словоформ c их частотами.
Для английских слов на корпусе 3'825'715 слов (ROCStories) и словаре 10'180 (см. файл 100KStories.zip), имеем:
order: 1 2 3 4 5 6 perplexity: 479.75 156.73 117.26 112.24 112.22 112.30Результаты можно улучшить, если вычислять n-граммы и перплексию по предложениям (в ROCStories они выделены).
Общие проблемы марковских моделей
Кроме указанных выше проблем больших словарей, существует ряд концептуальных ограничений марковских моделей.
- Язык, хотя и является линейной последовательностью слов, по своей природе имеет древесную, иерархическую структуру (как в рамках одного предложения, так и в логике всего текста). Например, в предложении "она быстро повернулась и радостно ему улыбнулась" окончания "ась" определяются словом "она" и слабо зависят от расстояния к нему.
- Марковские модели являются символьными. На уровне слов, в них изначально не учитыватеся морфологическая и семантическая близость слов. Например "любил" и "любила" (морфология) или "яблоко" и "груша" (семантика) независимые объекты, характеризующиеся только номером слова в словаре. Эти проблемы частично преодолевает векторное представление слов.
Приложение
Древесное представление n-грамм
Напишем на Python код, который вычисляет совместные и условные вероятности, для последовательности букв или слов. При анализе текста будем строить дерево встречаемых последовательностей и запоминать число таких встреч. Рассмотрим такое дерева на примере текста "мама_мыла_раму" (уровень символов).
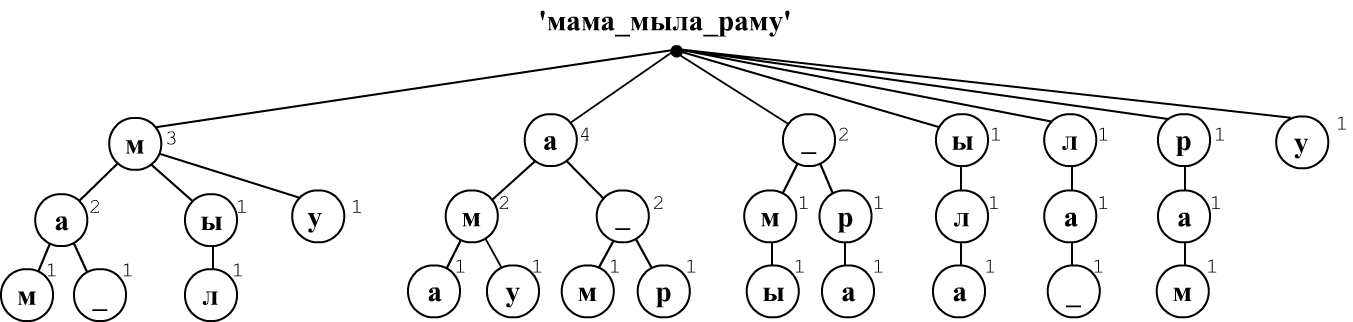
Пусть мы ограничились триграммами (необходимыми для вычисления совместных $P(x_1,x_2,x_3)$ и условных $P(x_1,x_2\Rightarrow x_3)$ вероятностей). Будем скользить по тексту окном в три символа, сдвигаясь на один символ. Первая последовательность "мам" даёт первую ветку дерева root -> м -> а -> м. В каждом узле записываем единицу. Следующая последовательность "ама" породит ещё одну ветку, выходящую из корня. Третья последовательность "ма_" начинается как первая ветка, поэтому первые два её узла увеличат счётчки в "м" и "а", а второй узел "а" расщепиться на две ветки (для символов "м", "_").
Несложно видеть, что условная вероятность $P(\mathbf{ма}\Rightarrow \mathbf{м})$ равна отношению числа в нижнем узле "м" к числу в предшествующем ему узле "a", т.е. 1/2=0.5. Совместная вероятность $P(\mathbf{мам})$ равна отношению числа в последнем узле к общему числу последовательностей длины 3. Это же дерево даёт более короткие условные или совместные вероятности: $P(\mathbf{м} \Rightarrow \mathbf{а}) = P(\mathbf{ма})/P(\mathbf{а})=2/3$.
На Python будем хранить каждый узел в форме словаря всех выходящих из него веток с указанием числа count попадания в эту ветку от корня: words = { word: [count, words], ...}. Словарь word имеет такую же структуру. Например, дерево выше начинается следующим образом:
{'м': [3, {'а': [2, {'м': [1, {}],
'_': [1, {}] }],
'ы': [1, {'л': [1, {}]} ]]
}
],
...
}
Класс NGramsCounter
Приведём класс NGramsCounter, который подсчитывает условные и совместные вероятности максимальной глубины order. Словами могут быть символы, строки или числа (индексы слов).
class NGramsCounter:
def __init__(self, order = 1):
self.order = order # глубина дерева (макс. длина n-grams)
self.root = {} # корень дерева (наш словарь)
self.ngrams= [0]*(order+1) # число n-grams диной n=1,2,...,order
Метод add добавляет новые примеры из списка слов lst. Если словами являются символы, то lst может быть строкой, иначе это обязательно спиcок.
def add(self, lst):
for n in range(self.order): # сколько каких n-grams добавилось
self.ngrams[n+1] += max(len(lst) - n , 0)
for i in range( len(lst) ): # бежим по тексту
node = self.root
for n, w in enumerate(lst[i: i+self.order]):
if w in node: node[w][0] += 1 # это слово уже было
else: node[w] = [1, {}] # новое слово
node = node[w][1] # на следующий узел дерева
Метод prob получает на вход список слов lst и возвращает условную вероятность P(lst[0],...,lst[len-2] => lst[len-1]), при len==1: P(lst[0]), если cond = True или безусловную вероятность при cond = False Если слова это символы, то lst может быть строкой, иначе это список.
def prob(self, lst, cond=True):
n_cur, n_prv, _ = self.counts(lst)
if n_cur == 0:
return 0 # слово не нашли - вероятность 0
return n_cur/(n_prv if cond else self.ngrams[len(lst)])
Полный код класса (с дополнительными проверками и другими методами) можно найти в my_ngrams.py.
Примеры использования NGramsCounter
counter = NGramsCounter(3) # будет 1,2,3 - грамм
counter.add('мама мыла раму') # подсчитываем n-граммы букв
print("размер словаря:", len(counter.root)) # 7
print("слова словаря:", counter.branches()) # [('м', 4), ('а', 4), ...]
print(counter.ngrams[1:]) # [14, 13, 12] число n-грамм n=1,2,3
print(counter.unique() ) # [7, 10, 12] уникальных n-грамм
N1, N2, _ = counter.counts('м') # N1 раз была 'м', N2 - длина текста
print("N('м'), N = ", N1, N2) # 4, 14
print("P('м') = ", counter.prob('м')) # 0.2857 = 4/14 = N1/N2
N1, N2, _ = counter.counts('ма') # N1 раз было 'ма', N2 - было 'м'
print("N('ма'),N('м') = ", N1, N2) # 2, 4
print("P('м=>а') = ", counter.prob('ма')) # 0.5 = 2/4 = N1/N2
print("P(ма=>м) = ", counter.prob('мам')) # 0.5 = 2/4 условная
print("P(мам) = ", counter.prob('мам', False))# 0.083 = 1/12 совместная
print(counter.branches('ма')) # [('м', 1), (' ', 1)] что после ма
counter.all_branches()
# [(['м', 'а', 'м'], 1), (['м', 'а', ' '], 1),... все ветки
Вероятности в класса NGramsCounter вычисляются как простое отношение N1/N2. Для более продвинутых способов следует использовать наследников от класса Markov.
Языковые модели содержат в себе counter, который наполняется в функциях add. Но можно им передать и внешний counter, что удобно при использовании нескольких моделей:
lm = MarkovLaplas(beta=1, order=3, counter=counter)
print(lm.counter.prob("ру")) # 0
print(lm.prob("ру")) # 0.125 = (0+1)/(1+7)
print(lm.perplexity("мама умыла раму")) # 4.886
Доступны следующие языковые модели:
- Markov
- MarkovLaplas
- MarkovInterpolated
- MarkovLaplasInterpolated
- MarkovBackoff
