ML: Комбинаторика и вероятности
Введение
При вычислении вероятностей элементарных событий часто требуется посчитать число возможных вариантов. Подобной деятельностью занимается комбинаторика. Это довольно своеобразный раздел математики. Решаемые им задачи выглядят очень сложными, до тех пор, пока не предъявлено их решение. Сразу после этого они кажутся абсолютно элементарными. Этот документ продолжает введение в теорию вероятностей и посвящён элементам комбинаторики и некоторым важным распределениям вероятностей.
Число перестановок
Число возможных перестановок $n$ пронумерованных объектов равно
факториалу от числа объектов:
$$
n!=n\cdot(n-1)\cdot....\cdot 1.
$$
Действительно, первый объект (справа шары) можно поставить
на одну из $n$ позиций. Для каждого из этих вариантов второй объект можно поставить
на одно из $n-1$ оставшихся свободных позиций.
Это делается $n\cdot(n-1)$ способами. Для каждого из них, третьему объекту остаётся $n-2$ позиций,
и т.д.
Удобно считать, что $0!=1!=1$. При больших $n$ факториал $n!$ растёт очень быстро и справедлива приближённая формула Стирлинга: $$ \ln n! \approx n\ln n - n + \ln\sqrt{2\pi n} + \frac{1}{12 n}, $$ которая хорошо работает даже при малых $n$. Например, $\ln 5! = 4.78749$, а формула Стирлинга даёт $4.7875\underline{1}$.
◊ Сколькими способами можно рассадить $n$ человек за столом?
Число перестановок людей равно $n!$. При этом не играет роли,
сидят они вдоль прямоугольного стола или вокруг круглого.
Число размещений
Пусть в закрытой урне есть $n$ пронумерованных шаров.
Из урны случайным образом, последовательно достают $m \le n$ шаров (без возврата).
Найдём число различных результатов такой процедуры.
Первым может быть вытащен шар с любым номером $1,...,n$. Для каждого из них,
вторым может быть один из $n-1$ оставшихся шаров и т.д.
Полученную величину называют размещениями $m$ по $n$:
$$
A^m_n = n\cdot (n-1)\cdot\,...\cdot (n-m+1) = \frac{n!}{(n-m)!},
$$
где произведение умножено и разделено на $(n-m)!$. На рисунке справа $n=3$, $m=2$ и $A^2_3=6$.
Обратим внимание, что результаты вытаскивания можно представить в виде $A^m_n$ различных $m$-ок
несовпадающих целых чисел
$(x_1,...,x_m)$, $x_i\neq x_j$, значения которых лежат в диапазоне $1\le x_i\le n$.
Число сочетаний
Пусть в урне есть $n$ пронумерованных шаров. Мы вытаскиваем (без возврата) $m$ шаров, не интересуясь их порядком.
Для однозначности, будем считать, что в конце шары упорядочиваются по возрастанию номера:
$(x_1 \lt x_2 \lt ....\lt x_m)$, где $1 \le x_1\le n$.
Число таких $m$-ок называется сочетаниями $m$ по $n$.
Так как $m$ пронумерованных объектов можно переставить $m!$ способами, то теперь величины $A^m_n$ необходимо уменьшить в $m!$ раз (все их перестановки не важны). В результате получаются биномиальные коэффициенты: $$ C^m_n = \frac{n!}{m!\,(n-m)!}. $$ Несложно видеть, что $C^n_n=1$ (просто достали все шары), а $C^1_n=n$ (вытащили один из $n$ шаров).
Бином Ньютона является производящей функцией для $C^m_n$ (коэффициенты её разложения в ряд по $x$ дают $C^m_n$): $$ (1+x)^n ~=~ 1 +\frac{n}{1!}\,x+\frac{n\,(n-1)}{2!}\,x^2 +...+ x^n ~=~\sum^n_{m=0} C^m_n\, x^m. $$ Приведём также несколько полезных тождеств: $$ C^m_n=C^{n-m}_n,~~~~~~~~~~~~C^{m+1}_{\,n\,+1} - C^{m+1}_{\,n} = C^m_n,~~~~~~~~~~~~~ \sum^n_{m=0} C^m_n = 2^n,~~~~~~~~~~~~~ \sum^n_{m=0} (C^m_n)^2 = C^n_{2n}. $$ Первые два следуют из определения, а последний - из производящей функции.
◊ Сколько существует последовательностей нулей и единиц длины $n$ с ровно $m$ единицами?
Таких последовательностей будет $C^m_n$. Так, для $n=4$, $m=2$, $C^2_4=6$ это: $1100$, $1010$, $1001$, $0110$, $0101$, $0011$.
Действительно, сделаем единицы различимыми (пронумеруем их). Первую единицу можно поставить на одно из $n$ мест.
Вторую, на одно из $n-1$ оставшихся мест и т.д., т.е. всего $~~~n\cdot (n-1)\cdot...\cdot (n+m-1)$ способами,
которые следует разделить на $m!$ (единицы неразличимы - все их перестановки эквивалентны).
Возможно также следующее рассуждение. Возьмём некоторую последовательность (выше, например, $1100$).
Все её вариации - это $n!$ перестановок $n$ цифр, из которых неразличимы $m!$ перестановок $m$ единиц
и $(n-m)!$ перестановок $n-m$ нулей. Поэтому имеем $n!/m!(n-m)!=C^m_n$ вариантов.
Бинарные последовательности
возникают в биномиальном распределении и при выводе распределения Ферми
(размещения по $n$ состояниям $m$ фермионов, которые не могут иметь одинакового состояния).
Число композиций
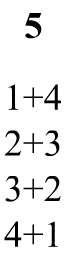✒ Полезным соотношением является количество возможных разложений (композиций)
числа $n$ на $k$ слагаемых: $n_1+...+n_k = n$. Пусть $n_i \gt 0$.
Представим число $n$ как $n$ единиц, разделённых пустыми местами: $1\square 1\square 1$.
На этих $n-1$ местах должны стоять $k-1$ запятых, разделяющих слагаемые, а в оставшихся - знаки плюс,
которые формируют эти слагаемые Например $3 = 1+2$ это $1\,,\,1+1$. Так как запятые неразличимы,
число
сочетаний (способов расстановки) запятых равно $C^{k-1}_{n-1}$. Если некоторые из $k$ слагаемых $n_i$ могут быть нулями, то сумму следует переписать так:
$(\tilde{n}_1-1)+...+(\tilde{n}_k-1)=n$ или $\tilde{n}_1+...+\tilde{n}_k=n+k$, где все $\tilde{n}_i \gt 0 $.
Таким образом:
$$
\text{Число композиций}~~~~
n_1+...+n_k = n~~~\text{равно}~~~~~~~~~
\left\{
\begin{array}{lll}
C^{k-1}_{n-1}, & если & n_i \gt 0\\
C^{k-1}_{n+k-1},& если & n_i \ge 0\\
\end{array}
\right..
$$
◊ Сколькими способами можно разложить $m$ неразличимых шаров по $n$ пронумерованным ящикам?
Обозначим через $N_i$ число шаров в $i$-м ящике. Тогда $N_1+...+N_n=m$, где $N_i\ge 0$ (в ящике шаров может не быть).
Поэтому число вариантов размещения равно $C^{n-1}_{m+n-1}$.
Эта задача лежит в основе вывода квантового распределения Бозе-Эйнштейна
(размещения $m$ тождественных бозонов по $n$ состояниям).
◊ Пусть сессия длится $d$ дней и состоит из $x$ экзаменов. По правилам,
после экзамена должен быть хотя бы один день на отдых. Какова вероятность
того, что какой-то экзамен выпадет на первый день сессии (при случайном формировании расписания)?
Добавим к сессии один день, который всегда будет выходным. Пары дней ($x$ штук) экзамен плюс выходной: $(э,в)$ разместим
внутри сессии, разделив их $d_i\ge 0$ днями: $d_1(э,в)d_2(э,в)d_3....(э,в)d_k,~$ где
$k=x+1$ и $d_1+...+d_k=n=d+1-2\,x$. Так как $d_i\ge 0$,
число возможных расписаний равно $N = C^{k-1}_{n+k-1}\cdot x! = A^{x}_{d+1-x}$.
Аналогично вычисляется число расписаний
с экзаменом в первый день: $(э,в)d_1(э,в)d_2....(э,в)d_k$. Теперь $k=x$ и $N_1 = C^{x-1}_{d-x}\cdot x! = x\, A^{x-1}_{d-x}$.
Поэтому искомая вероятность $P=N_1/N = x \, A^{x-1}_{d-x}/A^{x}_{d-x+1} = x/(d-x+1).$
Вытаскивание с возвратом
Будем вытаскивать $m$ шаров из урны, считая, что номер шара записывается, после чего он опять возвращается в урну. В отличии от вытаскиваний без возврата, номера в списке могут повторяться. Если мы отслеживаем порядок вытащенных шаров, каждая комбинация является числом с $m$ разрядами в $n$-ричной системе исчисления: $(x_1x_2...x_m)$, где $n$ - число шаров в урне. Количество таких чисел равно $n^m$. Действительно, возможно $n$ "цифр" в первом разряде. Для каждой такой возможности во втором разряде снова может быть $n$ "цифр" и т.д.: $n\cdot n\cdot ...$ ($m$ раз). Можно также представлять дерево, из корня которого выходят $n$ веток (первая "цифра"), из каждой ветки снова выходит $n$ веток (вторая "цифра") и т.д.
Сложнее ситуация когда порядок вытащенных шаров не отслеживают, перемешав и упорядочив их в конце. Таким образом, необходимо найти число всех возможных $m$-ок вида $(x_1\le x_2 \le ...\le x_m)$, где $1 \le x_i \le n$. Разделить $n^m$ на $m!$, как в ситуации с сочетаниями, нельзя, т.к. в последовательностях могут встречаться одинаковые номера (вместо $\lt$ стоят $\le$).
Обозначим число искомых комбинаций как $(m,n)$.
Очевидно, что $(1,n)=n$. Докажем по индукции, что
$$
(m,n) = C^m_{n+m-1}.
$$
Найдём число $(m+1,n)$ последовательностей $(x_1\le ...\le x_{m+1})$.
Для $x_1=1$ будет $(m,n)$ вариантов $(x_2\le ...\le x_{m+1})$.
Число последовательностей с $x_1=2$ равно $(m,n-1)$, т.к. номера в списке
$(x_1\le ...\le x_{m+1})$, $2\le x_i\le n$ можно
уменьшить на $1$, получив $1\le x_i\le n-1$.
Аналогично далее до $(m,1)$ при $x_1=n$:
$$
(m+1,n) ~=~ (m,1)+\sum^n_{k=2} (m,k) ~=~ C^{m}_{m}+\sum^n_{k=2} C^m_{k+m-1} ~=~
C^{m}_{m} + \sum^n_{k=2} (C^{m+1}_{k+m}-C^{m+1}_{k+m-1}) = C^{m}_{m} - C^{m+1}_{m+1}+ C^{m+1}_{n+1},
$$
где во втором равенстве подставлены $(m,n) = C^m_{n+m-1}$, а в третьем
учтено второе тождество для биномиальных коэффициентов.
В полученной сумме разностей сокращаются все слагаемые, кроме части первого и последнего. Так как $C^m_m = C^{m+1}_{m+1}$,
получаем $C^{m+1}_{n+m}$.
Таким образом, из $(1,n)$ и $(m,n)$, мы вывели выражение для $(m+1,n)$.
Поэтому $(m,n) = C^m_{n+m-1}$ для любого $m$. □
Гипергеометрическое распределение
Пусть урне есть $M$ белых неразичимых шаров и $N-M$ черных (также неразличимых) шаров. Из урны достают $n$ шаров без возврата. Найдём вероятность того, что $m$ из них окажутся белыми. Выбрать $n$ шаров из урны с $N$ шарами можно $C^n_N$ способами (игнорируя их цвет). Число способов выбрать $m$ шаров из $M$ белых равна $C^{m}_{M}$. Для каждого такого способа есть $C^{n-m}_{N-M}$ возможностей выбрать $n-m$ шаров из $N-M$ черных. Поэтому искомая вероятность равна гипергеометрическому распределению: $$ P(N,M,n\to m)=\frac{C^{m}_{M}\,C^{n-m}_{N-M}}{C^n_N}. $$ Минимальное значение $m$ будет когда из урны достанут все чёрные шары, а максимальное - когда все белые. Поэтому $m$ лежит в интервале $[\max(0,\,n-(N-M)),~\min(n,\,M)]$.
◊ Найти вероятность угадать $m=0...5$ цифр розыгрыша в лотерею $M=5$ из $N=36$.
Можно считать, что выпавшие $M$ шаров на розыгрыше уже известны (но нам их номера не сообщили).
Эти шары красят в белый цвет, а остальные $N-M$ в чёрный и кладут в урну.
Мы случайно достаём $n=M=5$ шаров. Из них $m=0,...,n$ будет белыми (выигрышными)
с вероятностью $P(36,5,5\to m)=C^{m}_{5}\,C^{5-m}_{31}/C^5_{32}$.
Биномиальное распределение
Пусть вероятность события равна $p$. Найдём вероятность $P_n(m)$ наблюдать это событие $m$ раз в $n$ испытаниях. Вероятность конкретной последовательности наблюдений (0010011 - нет,нет,да,...) равна $p^m \,(1-p)^{n-m}$. Таких последовательностей будет $C^m_n$ штук, что приводит к биномиальному распределению или распределению Бернули: $$ P_n(m)=C^m_n\,p^m \,q^{n-m},~~~~~~~~~~~q=1-p,~~~~~~~~~~~\sum^n_{m=0} P_n(m) = (p+q)^n = 1. $$
Учитывая бином Ньютона, несложно получить производящую функцию для средних:
$$
\langle m^k \rangle = \sum^n_{m=0} m^k\,P_n(m),~~~~~~~~~~~(p\,e^t + q)^n = \sum^n_{m=0} C^m_n\, e^{tm}\,p^m\,q^{n-m} = \sum^\infty_{k=0} \langle m^k \rangle \,\frac{t^k}{k!},
$$
где последнее равенство получено разложением экспоненты в ряд Тейлора. Беря производные по $t$
от $(p\,e^t + q)^n$ в точке $t=0$, получаем следующие выражения для среднего, дисперсии,
и скоса (асимметрии):
$$
m_{ср}=\langle m \rangle = np,~~~~~~~~~~
D=\langle (m-m_{ср})^2 \rangle=npq,~~~~~~~~~~
\frac{\langle (m-m_{ср})^3 \rangle}{D^{3/2}}=\frac{1-2p}{\sqrt{npq}}.
$$
Чем ближе скос к нулю, тем симметричнее распределение относительно среднего значения.
Для $p=1/2$ распределение симметрично (биномиальные коэффициенты симметричны, а $p^m q^{n-m}=1/2^n$).
Отметим, что урна гипергеометрического распределения, при $M,N\to \infty$ и $N/M \to p$ может рассматриваться как генератор случайного события, имеющего вероятность $p$. В этом пределе гипергеометрическое распределение стремится к биномиальному. В свою очередь, биномиальное распределение в двух важных предельных случаях переходит в распределение Пуассона и Гаусса (нормальное распределение). Рассмотрим их подробнее.
Распределение Пуассона
Пусть $n\to \infty$ и $p\to 0$ так, что $np=\lambda=\text{const}$.
Подобный предел возникает, например, при радиоактивном распаде (много атомов $n$,
а вероятность распада $p$ каждого из них мала) или при отказах на обслуживание (много запросов $n$
и мала вероятность отказа $p$ в каждом из них).
Запишем биномиальное распределение:
$$
P_n(m)=\frac{n\,(n-1)\,...\,(n-m+1)}{m!}\,p^m \,q^{n-m} =
\frac{(np)^m \,q^{n-m}}{m!}\,\Bigr(1-\frac{1}{n}\Bigr)\,...\,\Bigr(1-\frac{m-1}{n}\Bigr)
$$
и устремим $n\to \infty$ и $p\to 0$. Тогда $q^{n-m}\to q^n = (1-\lambda/n)^{n}\to e^{-\lambda}$ (замечательный предел) и
мы приходим к распределению Пуассона:
$$
P(m) = \frac{\lambda^m}{m!}\,e^{-\lambda},~~~~~~~~~~~~~~~~~~~~~\sum^\infty_{m=0} P(m) =e^\lambda\, e^{-\lambda}= 1.
$$
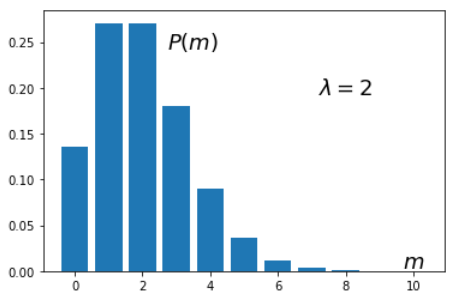Параметр распределения $\lambda$, обычно, находится из анализа данных.
Он имеет смысл среднего значения $m_{ср}=\lambda$ и дисперсии $D=\langle (m-m_{ср})^2 \rangle =\lambda$
(это следует при $n\to \infty$, $p\to 0$ из статистик для биномиального распределения). Скос равен $\lambda^{-1/2}$
Чем больше $\lambda$, тем распределение будет симметричнее относительно $m_{ср}$. При малых $\lambda$,
максимум распределения прижимается к нулю и имеет длинный "хвост" вправо (большая ассиметрия).
При использовании пуассоновского распределения, события обычно наблюдают в течении некоторого времени $t$. Поэтому удобно перейти к числу событий в единицу времени: $\lambda = np = \mu t$ (чем больше $t$, тем больше наблюдений $n$). Вероятность того, что за время $t$ произойдёт $m$ событий в этом случае равна: $$ P(m) = \frac{(\mu t)^m}{m!}\,e^{-\mu t}. $$ С вероятностью $e^{-\mu t}$ за время $t$ не произойдёт ни одного события и с вероятностью $1-e^{-\mu t}$ произойдёт хотя бы одно событие.
Так как $\langle m \rangle = \mu t$, за малый интервал времени $dt$ произойдёт $d\langle m \rangle = \mu \,dt$ событий. Поэтому параметр распределения $\mu = d\langle m \rangle \,/ \,dt$ называют интенсивностью пуассоновского потока.
Нормальное распределение
✒ Рассмотрим теперь предел больших $n$ и конечных $p$ при $m\sim \,np=\langle m \rangle$ ($m$ находится около своего среднего значения). Найдём сначала разложение в ряд по $x$ факториала $(N+x)!$ при $N \gg x$. По определению: $$ \ln(N+x)! = \ln[N!(N+1)...(N+x)] = \ln N! + \sum^x_{k=1}\,\ln(N+k) = \ln N! + x\ln N + \sum^x_{k=1}\,\ln\Bigr(1+\frac{k}{N}\Bigr). $$ Учитывая разложение $\ln(1+x)=x+...$ при малых $x$ и сумму $1+2+...+x=x(x+1)/2$ (арифметическая прогрессия), окончательно получаем: $$ \ln(N+x)! = \ln N! + x\ln N + \frac{x(x+1)}{2N} + O\Bigr(\frac{1}{N^2}\Bigr). $$ Отметим, что положив $x=dN$ несложно получить уравнение $d\ln(N!)/dN = \ln N + 1/2N$, откуда следуют первые три слагаемых формулы Стирлинга (с точностью до постоянного множителя).
Введём теперь $x$, равное отклонению $m$ от среднего значения $np$. При этом $m=pn + x$ и $n-m = qn - x$: $$ \ln P_n(m) = \ln n! - \ln(pn+x)! - \ln(qn-x)! + (pn+x)\,\ln p + (qn - x)\,\ln q. $$ Используя формулу для $\ln(N+x)!$, получаем: $$ \ln P_n(m) = \ln P_n(np) -\frac{x^2+(1-2p)\,x}{2D}, $$ где первое слагаемое соответствует постоянным членам разложения при $x=0$ и $D=n\,p\,q$ - дисперсия биномиального распределения. Множитель $1-2p$ при линейном по $x$ члене меняется в интервале $(-1,...,1)$ и характеризует асимметрию биномиального распределения. Это слагаемое даёт небольшой вклад (и при $p=1/2$ пропадает). Действительно, так как $x=1,2,3,...$, имеем $x^2\gg (1-2p)\,x$ уже для $x=2$ (например, для $p=1/4$ будет $4 \gg 1$). Чем больше $x$, тем меньше вклад этого слагаемого.
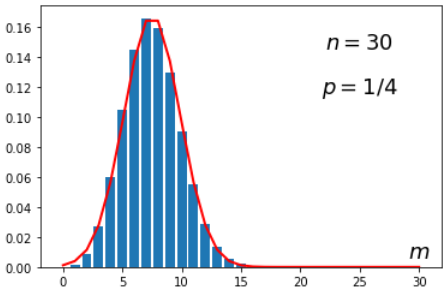Таким образом, хорошим приближением к биномиальному распределению при больших $n$ и $p\sim 1/2$
является нормальное распределение:
$$
P_n(m)\approx \frac{1}{\sqrt{2\pi D}}\,e^{-(m-np)^2/2D},
$$
где нормировочный множитель $1/\sqrt{2\pi D}$ получен интегрированием по $x$ от $-\infty$, до $\infty$
(экспонента быстро убывает). Такое распределение названо "нормальным",
потому, что оно часто возникает в различных практических задачах. Например,
если измеряются значения некоторой величины $X$, которая подвержена большому числу
случайных и независимых внешних воздействий, она становится случайной с нормальным распределением.
Полезные интегралы
При работе с нормальным распределением часто возникает интеграл следующего вида:
$$
I = \int\limits^\infty_{-\infty} e^{-x^2} \,dx.
$$
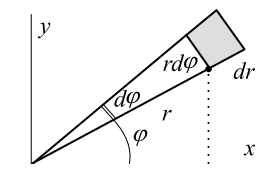Он вычисляется в полярных координатах $(r,~\phi):~x=r\cos \phi,~~y=r\sin \phi$, как двойной интеграл:
$$
I^2 = \int\limits^\infty_{-\infty} \int\limits^\infty_{-\infty} e^{-x^2-y^2} dx dy
= \int\limits_0^{2\pi} \int\limits^\infty_{0} e^{-r^2} r dr d\phi
= 2\pi \int\limits^\infty_{0} e^{-r^2} d\frac{r^2}{2} = \pi,
$$
где мы воспользовались тем, что в координатах $(r,~\phi)$ элемент площади равен произведению дуги $rd\phi$
на изменение радиуса $dr:~dxdy=rd\phi \, dr$.
Извлекая квадратный корень и делая замену $x \to x\sqrt{\alpha}$, получаем:
$$
~I(\alpha) = \int\limits^\infty_{-\infty} e^{-\alpha x^2} dx = \sqrt{\frac{\pi}{\alpha}}.
$$
Полезный приём - взятие производных правой и левой частей по параметру $\alpha$ для получения интегралов от чётных степеней $x^{2n}$.
Интеграл от нечетных степеней $x$, в силу антисимметричности подынтегральной функции, равен нулю.
Если выделить полный квадрат в выражении $-\alpha x^2+\beta x$, получается
следующий интеграл (при помощи замены $x'=x-\beta/2\alpha$ он сводится к $I(\alpha)$ ):
$$
~\int\limits^\infty_{-\infty} e^{-\alpha x^2+\beta x} ~dx = \sqrt{\frac{\pi}{\alpha}}~ ~e^{\beta^2/4\alpha}.
$$
Вычислим ещё один интеграл, взяв от него $n$ раз производную по $\alpha$:
$$
I(\alpha) = \int\limits^\infty_{0} e^{-\alpha x} dx = -\frac{1}{\alpha}~e^{-\alpha x}\biggr|^{\infty}_0 = \frac{1}{\alpha}
~~~~~~~~~~~
\Rightarrow~~~~~~~~~~~~~\int\limits^\infty_{0} x^n e^{-\alpha x} dx = \frac{n!}{\alpha^{n+1}}.
$$
Интегралы такого типа встречаются часто и для них введено специальное
обозначение в виде гамма-функции:
$$
~\Gamma(z) = \int\limits^\infty_{0} x^{z-1} e^{-x} dx.
$$
Интегрируя по частям, убеждаемся, что $\Gamma(z+1)=z\,\Gamma(z)$.
В частности, для целых аргументов: $\Gamma(n+1)=n!$.
Для полуцелых аргументов гамма-функция сводится к гауссовому интегралу. Так, $\Gamma(1/2)=\sqrt{\pi}$.
Из интегрального определения гамма-функции следует формула Стирлинга. Представим $x^ne^{-x}$ как $e^{f(x)}$. Функция $f(x)=-x+n \ln x$ имеет максимум в точке $x_0=n$, так как $f'(x_0)=-1+n/x_0=0$. Запишем её ряд в окрестности этой точки: $$ f(x)=f(n)+\frac{1}{2}\,f''(n)(x-n)^2+...~=~ -n + n\ln n - \frac{(x-n)^2}{2n}+... $$ Поэтому $$ n! \approx e^{-n + n \ln n} \int\limits^\infty_{0} e^{-\frac{(x-n)^2}{2n}} dx \approx e^{-n + n \ln n} \int\limits^\infty_{-\infty} e^{-\frac{(x-n)^2}{2n}} dx =e^{-n + n \ln n} \sqrt{2\pi n}. $$ Во втором интеграле нижний предел заменён на $-\infty$, так как при большом $n$ максимум экспоненты уходит далеко вправо и становится всё более узким, поэтому интеграл от $-\infty$ до $0$ практически равен нулю. Отсюда следуют первые три слагаемых формулы Стирлинга.
