Объяснение работы CNN

Введение

В этом документе анализируется как свёрточные нейронные сети формируют признаки при классификации изображений. Чтобы "интерпретируемость модели" была максимально ясной, будут рассмотрены очень простые датасеты:

Однако начнём мы с напоминания того, как старые, добрые полносвязные нейронные сети преобразуют пространство признаков.

Преобразование пространства признаков

Для наглядности рассмотрим объекты двух видов (синие и красные) с двумя признаками (ниже первый рисунок):

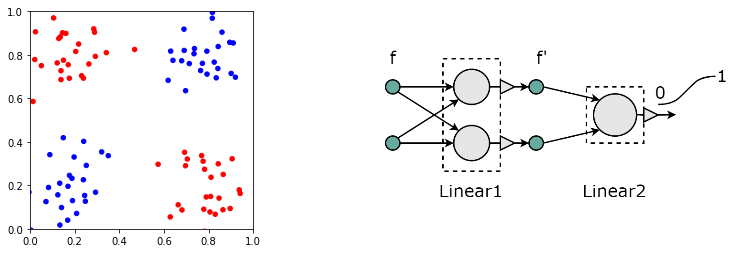
Этот "датасет" ни что иное как классический "xor". Напомним, что любая, даже самая сложная нейронная сеть, занимающаяся классификацией, в конце имеет линейный слой с числом выходов равных числу классов. В нашем примере два класса, поэтому достаточно одного выхода (с сигмоидом после него). Если на выходе получается 0, то это первый класс, а если 1, то второй. Подобный линейный классификатор является гиперплоскостью. Значение его выхода равно расстоянию от точек (примеров) до плоскости со знаком плюс, если точки находятся по направлению вектора нормали плоскости и со знаком минус, если против. Эта плоскость должна отделить примеры одного класса от примеров второго класса в финальном пространстве признаков.

Понятно, что в задаче "xor" сети с одним слоем недостаточно. Одной гиперплоскостью (в двумерии прямой) нельзя отделить синие объекты от красных. Поэтому нужен хотя бы один скрытый слой, занимающийся преобразованием пространства признаков: 

 Sequential:
    (0): Linear(in_features=2, out_features=2, bias=True)
    (1): Sigmoid()
    (2): Linear(in_features=2, out_features=1, bias=True)
    (3): Sigmoid()
В данной архитектуре скрытый (нулевой) слой имеет два нейрона. Поэтому, полученное на его выходе преобразованное пространство признаков снова будет двумерным. Обучим эту сеть и выведем "координаты" объектов (их новые признаки) на выходе первого сигмоида. Результат представлен ниже на первом рисунке:

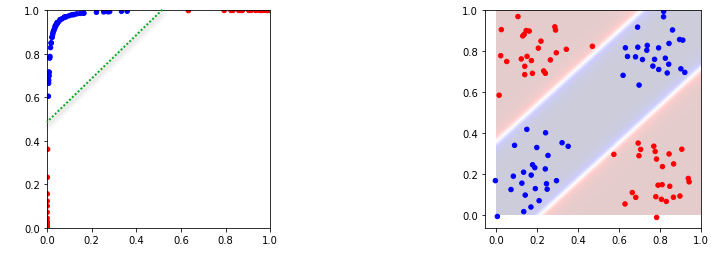
Как видно, сеть так деформировала пространство признаков, чтобы объекты разных классов стали линейно разделяемые. Соответствующую гиперплоскость (пунктирная линия) легко строит выходной слой. В конечном итоге исходное пространство признаков разбивается на три области (выше второй рисунок).

Преобразованное пространство признаков может иметь (и обычно имеет) большую размерность, по сравнению с исходным. Например, для датасета "xor" можно взять три нейрона в скрытом (первом) слое. В результате получаются три координаты объектов в новом пространстве признаков. Нарисуем их на 3D графике:

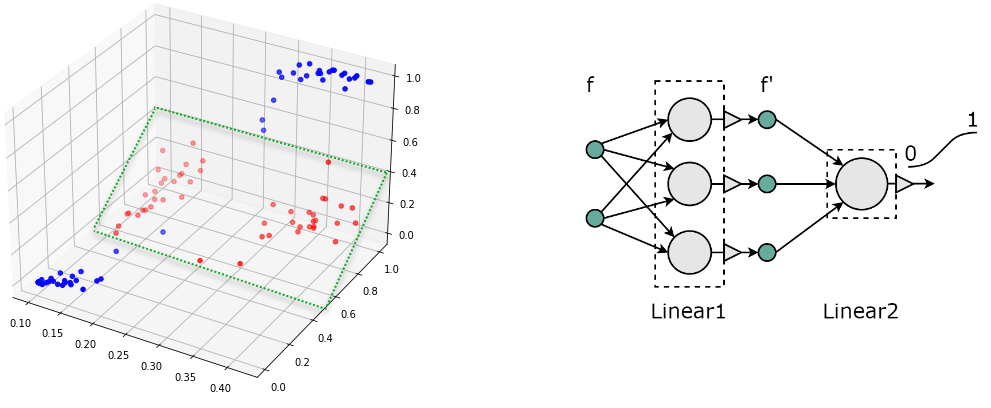
Как видно, все объекты (кроме одного) снова оказались линейно разделяемыми. Соответствующая 2D плоскость в 3D пространстве нарисована зелеными пунктирными линиями.

Наша трёхмерная интуиция не очень хорошо приспособлена к многомерным пространствам. Такие пространства очень большие :). Именно это приводит к возможности линейного разделения классов в сложных задачах. Обычно, чем больше признаков, тем лучше. Хотя, конечно, если какой-то признак является просто шумом, это может помешать классификации.

Ну и наконец, совсем тривиальное замечание. Если в исходных данных упущены какие-то важные признаки, то никакая нейронная сеть не построит линейно разделимое пространство признаков. А для "правильных признаков" архитектура сети может быть очень простой. Например, если бы в исходном датасете по-мимо координат точек $(x_1,x_2)$ был третий признак $x_3$, который "поднимает" все синие точки вверх, а красные опускает вниз по оси $x_3$, то для классификации достаточно было бы и линейной модели с плоскостью, описываемой уравненем $x_3=0$.
Но это уже другая история...

Фигуры без вращения

Перейдём к классификации изображений. Нарисуем три типа геометрических фигур (треугольник, квадрат, окружность). Каждую фигуру будем делать контурной или залитой. В результате получим 6 классов, которые должна научиться распознавать нейронная сеть. Размеры и положения фигур будут варьироваться:

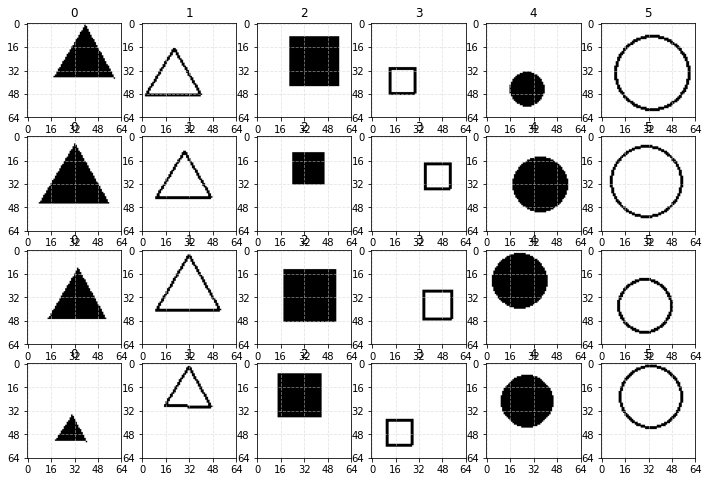
Всего датасет состоит из 12000 примеров (по 2000 на каждый класс). Из них 80% будут обучающими, а 20% тестовыми. Изображения имеют размер 64x64 = 4096 пикселей. Радиус фигур (в который они вписываются) случайно изменяется в диапазоне [12..28] пикселей. Положение фигуры на изображении также случайно. Для удобства интерпретации, фигуры полностью помещаются на изображении (хотя их небольшой заход "за край" изображения не сильно усложняет обучение). Фон имеет нулевое значение (но на рисунках обозначается белым цветом), а линии и заливка имеют единичное значение (на рисунках чёрный цвет).

Полносвязная сеть

Как известно, изображения можно классифицировать при помощи простых полносвязных сетей. Проверим это на нашем датаете. Оказывается, что линейная модель для этих геометрических фигур не учится вообще. Поэтому возьмём один скрытый слой с 1024 нейронами, что при 4096 признаках (пикселях = 64*64) порождает более четырёх миллионов параметров:

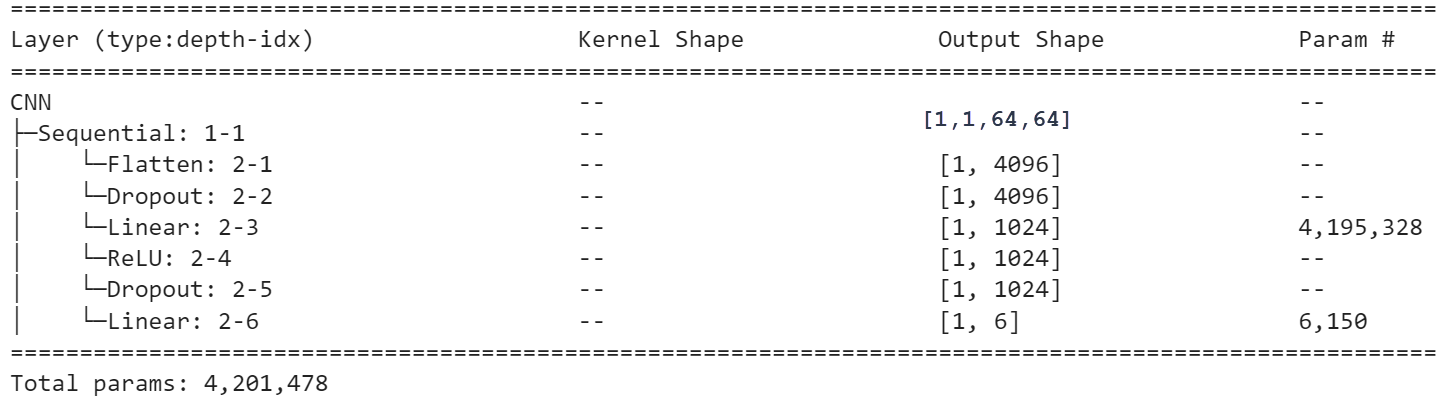
При классификации, на выходе сети необходимо поставить функцию softmax, но так как используется ошибка nn.CrossEntropyLoss() - при обучении softmax не нужен. Обучение теперь идёт более или менее успешно:

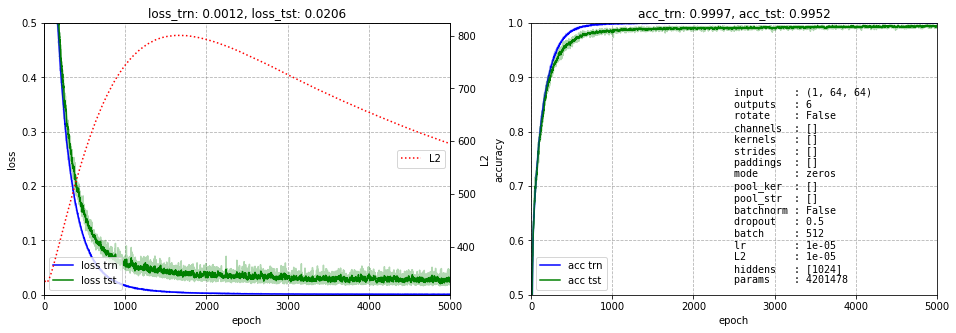
Здесь и далее на левом графике приведено значение ошибки обучения (синий - тренировочные данные, зелёный - тестовые). Тонкая красная линия - сумма квадратов весов сети (для контроля перевозбудимости нейронов и для её подавления L2-регуляризацией). На правом графике приведена точность (accuracy) на тренировочных данных (синий) и на тестовых (зелёный). Соответствующие цифры на последней эпохе обучения указаны над графиками.

На правом графике также выводятся гиперпараметры, определяющие архитектуру сети и параметры обучения. Пока значащими являются последние шесть. Отметим значение dropout=0.5 (обнуление с вероятностью 0.5 весов нейронов при обучении). Без этого гиперпараметра данная сеть сильно переобучается.

Интерпретация работы сети в 1024-мерном пространстве признаков проблематична. К тому же, с таким числом параметров может возникать эффект скрытого переобучения (хотя тестовые данные генерятся независимо от тренировочных, они, на самом деле, могут сильно пересекаться, в силу небольшого разрешения изображения и простоты геометрических форм). Таким образом, лучше воспользуемся свёрточными сетями.

Свёрточные сети

Вкратце напомним основные понятия. Свёрточный или конволюционный слой Conv2d является небольшим фильтром, который скользит по изображению, преобразуя его в новое изображение (того же или меньшего размера). Ниже приведены результаты работы чётырёх фильтров 3x3 над верхним изображением:

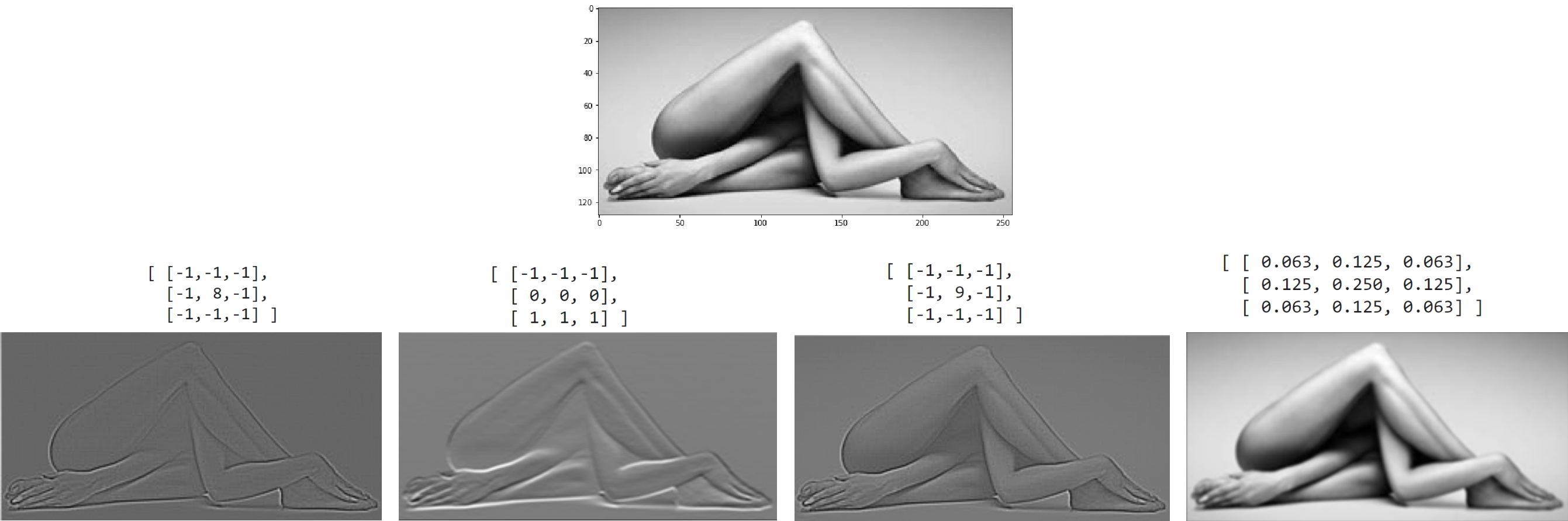
В общем случае фильтр - это 3-мерная матрица. На вход сети поступает изображение, которое обычно имеет один (градации серого) или три (RGB цвета) канала. Конволюционый слой на выходе может иметь произвольное число каналов. Ниже приведен пример, когда на вход слоя поступает два канала, а на выходе получается три:

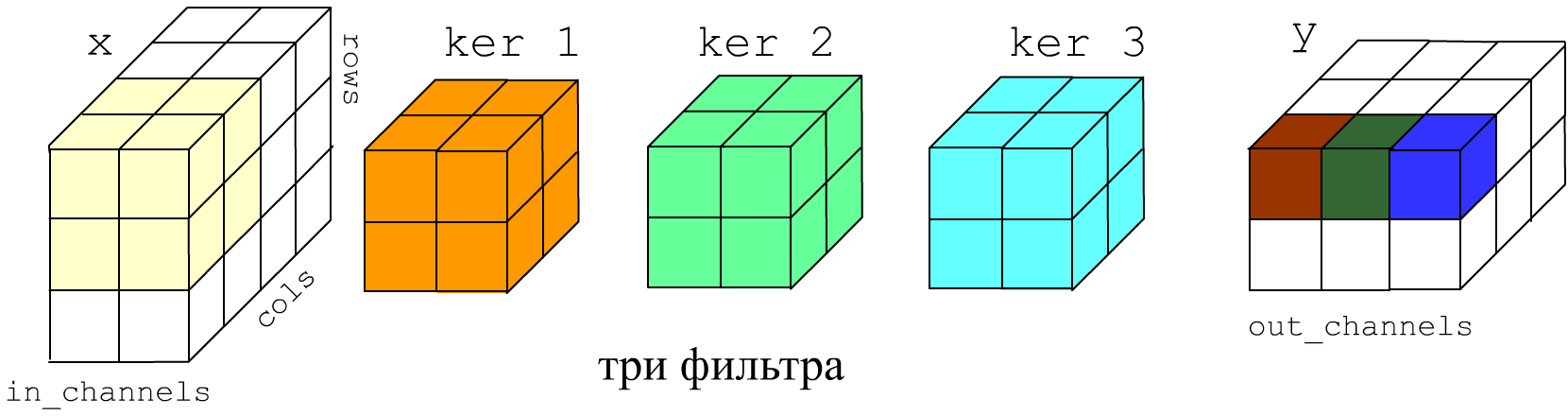
Для каждого выходного канала формируется обучаемая 3D матрица параметров (плюс смещение). Каждая из них независимо и на всю глубину производит вычисление результаты работы такого 3D фильтра.

Таким образом, при создании свёрточного слоя ключевыми параметрами являются число входных каналов (глубина фильтров), число выходных каналов (количество фильтров), размер ядра (ширина и высота фильтров) и шаг stride с которым фильтр скользит по стопке изображений (входных каналов): 

torch.nn.Conv2d(in_channels = 2, out_channels = 3, kernel_size = 2, stride=1, 
                padding = 0, padding_mode='zeros', dilation=1)

Технически важными являются параметр заполнения padding и параметр расширения dilation:

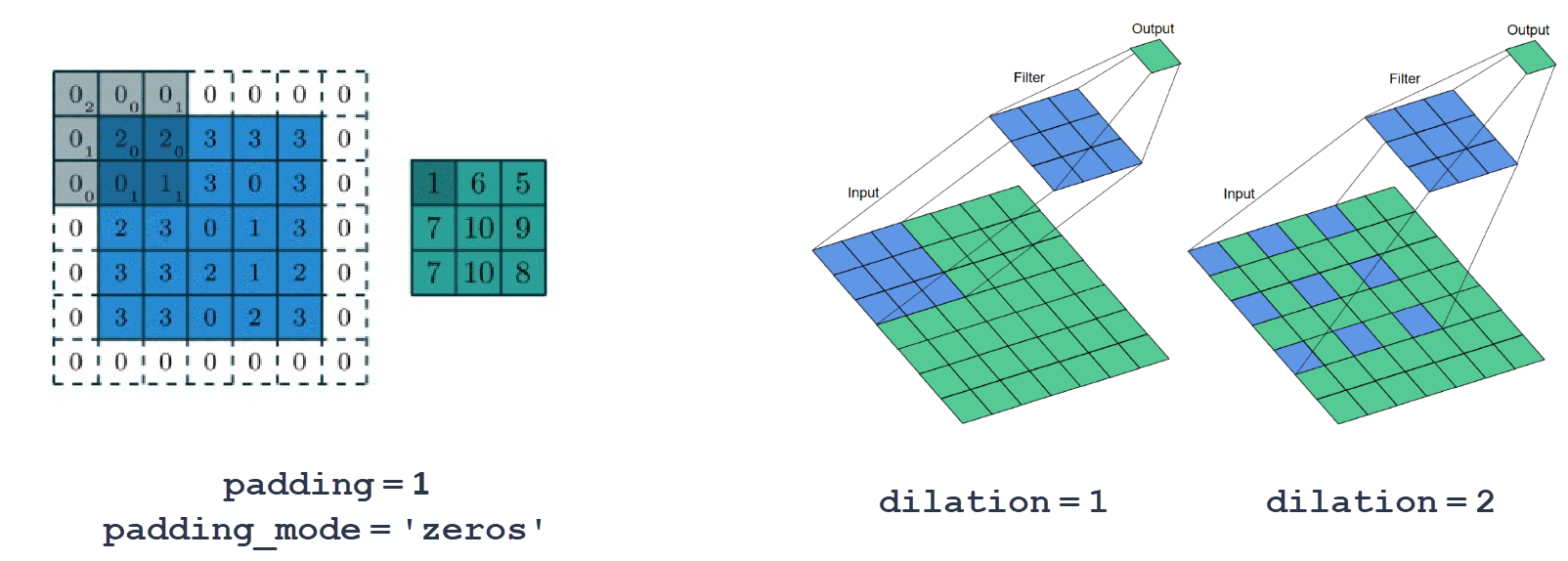
Если мы хотим, чтобы при конволюции размер изображения не менялся, следует окружить его рамкой из "фейковых" пикселей. Для ядра 3 следует взять padding = 1, для ядра 5 - padding = 2 и т.д.

Расширение (dilation) позволяет при том же ядре (и следовательно числе параметров) охватывать большую область изображения. Несмотря на "дырки", если фильтр скользит по изображению с единичным шагом (stride=1), в выходные каналы попадёт информация от всех пикселей входных каналов.

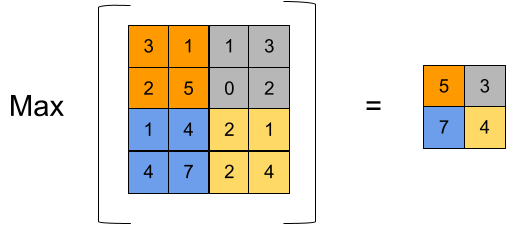Второй ключевой составляющей является слой max pooling. Он вычисляет максимальное значение пикселя на входном канале внутри своего ядра: 

torch.nn.MaxPool2d(kernel_size, stride=None, 
                   padding = 0, dilation = 1)
Как и конволюционный слой он имеет размер ядра и шаг. Число каналов на выходе всегда совпадает с числом каналов на входе. При этом максимальное значение вычисляется внутри каждого входного канала независимо. Таким образом, если Conv2d перемешивает все входные каналы, то MaxPool2d этого не делает. Понятно, что этот слой не содержит обучаемых параметров.

Кроме задачи уменьшения размера карты признаков (ширины и высоты стопки каналов), слой MaxPool2d также занимется выделением важных признаков (с максимальным значением). К тому же он делает сеть более устойчивой к небольшим сдвигам изображения (в пределах ядра MaxPool2d).

Обычно архитектура свёрточной сети содержит цепочку из блоков, состоящих из Conv2d (порождение фильтром новых признаков), ReLU (нелинейность), MaxPool2d (сужение карты признаков). Отметим, что сужение не обязательно делать при помощи слоя MaxPool2d. Если stride фильтра в Conv2d, например, равно 2, то выходные изображения будут в 2 раза меньше, а если не использовать заполнение (padding), то на каждой конволюции будет "откусываться" периметр карты.

Первая CNN-архитектура

Вернёмся к нашему датасету с геометрическими фигурами. Так как мы хотим увидеть что происходит на различных каналах во всех слоях, архитектуру сети максимально упростим:

При помощи паддинга конволюция сохраняет размер изображения. Пулинг (если он есть) всегда будет иметь размер ядра 2 и такой же шаг (stride), чтобы изображение уменьшалось в два раза по каждой оси. На графиках обучения это параметры pool_ker и pool_str. Шаг конволюции (в гиперпараметрах это strides) обычно будет единичным.

Ниже представлено обучение этой сети. Несмотря на небольшое число параметров (3168) она быстро учится и имеет ошибку менее 0.5%:

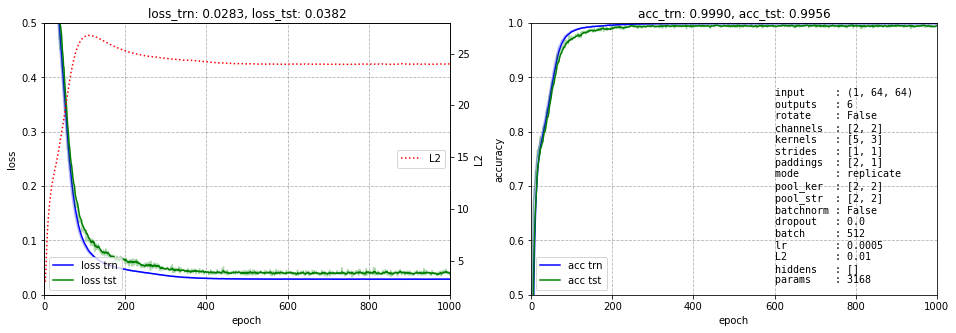
Интерпретируем слои CNN

У нас есть два слоя со структурой Conv2d - ReLU - MaxPool2d. Каждый слой содержит по два канала. Подадим на вход сети 12 изображений (по два от каждого класса) и нарисуем их "проекцию" на выходе слоя MaxPool2d:

Последние две строки картинок - это два канала выходного слоя (финальная карата признаков). Именно эти изображения далее превращаются (Flatten) в один линейный вектор 16*16*2 = 512 признаков, которые подаются на линейный классификатор (шесть гиперплоскостей в 512-мерном пространстве). Основное вклад в число параметров модели, как обычно, даёт именно этот классификатор (3078 параметров).

Как видно, первый канал финального CNN-слоя (предпоследний ряд картинок), просто повторяет исходные изображения (в более низком разрешении). Второй канал (последний ряд) уже выделяет некие признаки: для квадратов (как залитых, так и контурных) это горизонтальные линии, для треугольников - основание, а у окружностей их верхняя и нижняя части.

Можно также заметить, что эти же признаки (ещё не столь явно выраженные) независимо формируют два канала первого слоя.

Уменьшим размерность финальных признаков

Представить себе 512-мерное пространство непросто. Поэтому добавим ещё один слой с конволюцией и пулингом, так чтобы на нём было два канала размером 8x8 Углубление улуччшает обучаемость:

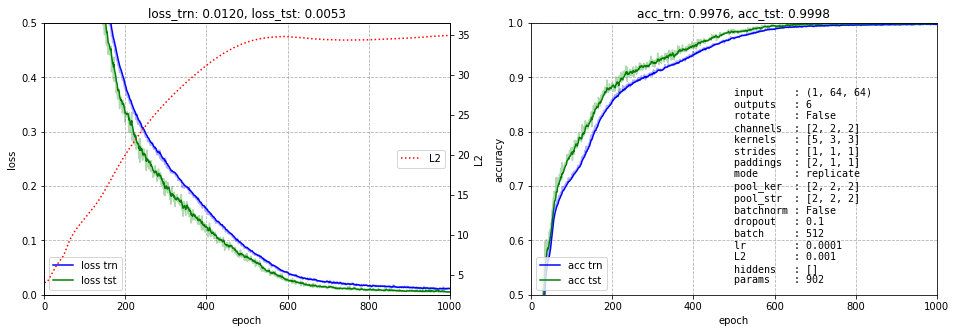
Выведем только результирующие каналы (на последнем пулинге):

Представить 8x8x2 = 128-мерное пространство стало безусловно проще. Как получается вектор координат точки конкретного примера в этом пространстве? Возмём первый пример (залитый треугольник). Первый пиксель первой карты признаков имеет нулевое значение (цвета инвертированны). Далее снова идут два нуля потом три не нулевых значения и снова нули. В результате получается что-то типа: $\mathbf{x} = (0,\, 0,\, 0,\, 0.2,\, 0.5,\, 0.3,\, 0,\, 0,\, 0,\, ...)$.

Углубим сеть

Чтобы нас не заподозрили в дипфобии, возьмём ещё более глубокую архитектуру с четырьмя свёрточными слоями. Чтобы картинки были красивыми (размера 16x16) мы, аналогично VGG будем ставить пулинг после пары слоёв. Число параметров увеличилось в четыре раза. Но это связано не с большим числом слоёв, а с большим числом каналов в них (на последнем слое после пулинга теперь 8 каналов, а не 2 как ранее:

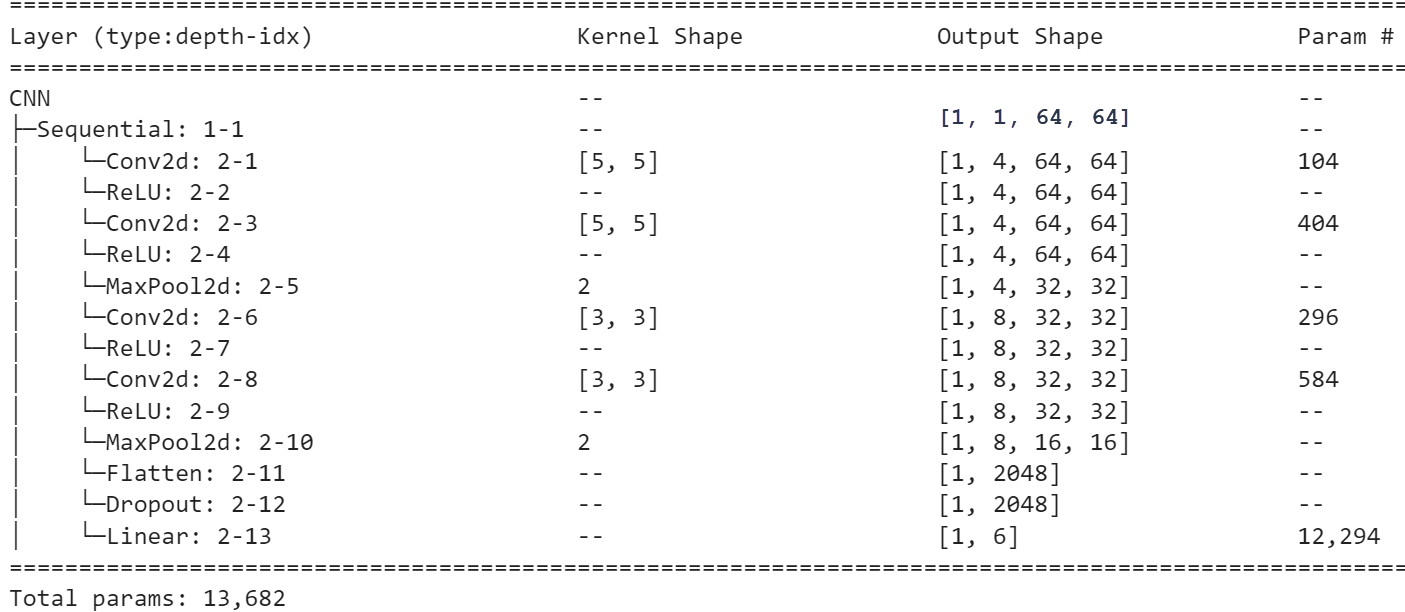
Сеть отлично обучается:

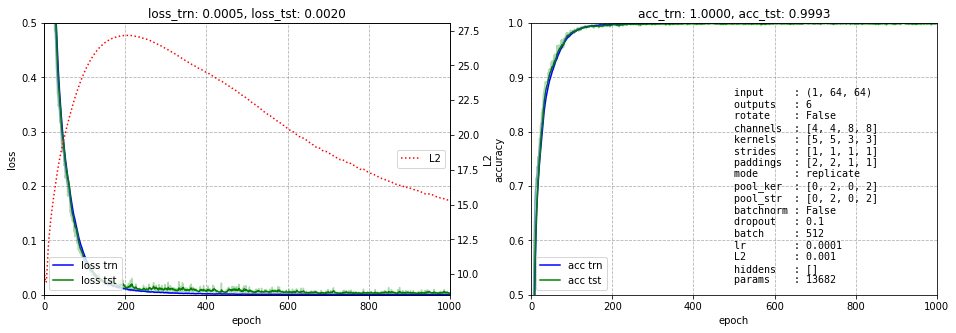
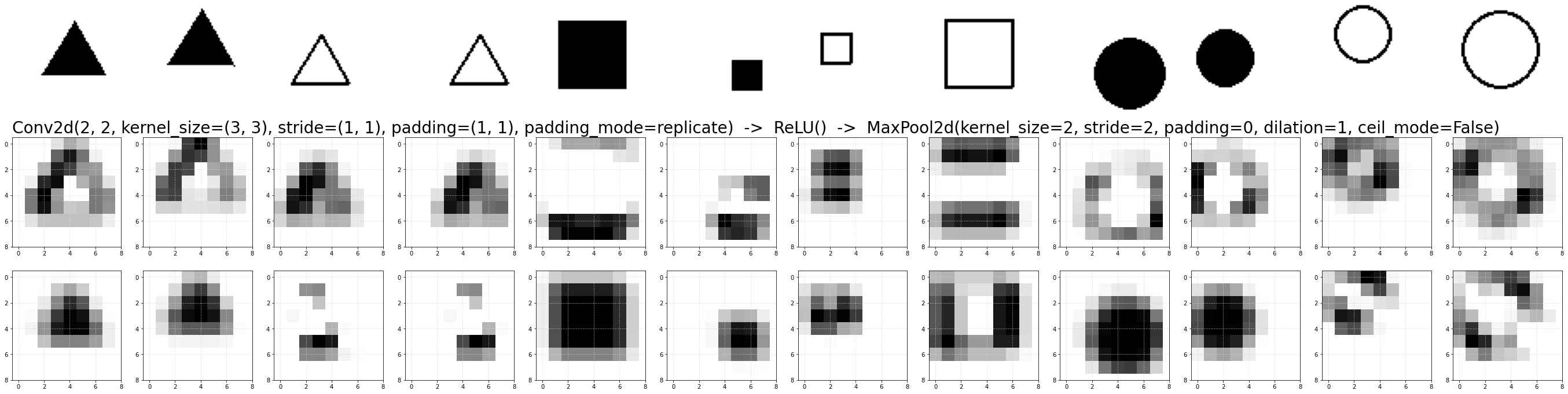
Так как слоёв теперь много, кроме входных изображений, выведем только результат на финальных восьми карт признаков (на последнем пулинге):

Первое, что бросается в глаза - это дублирование признаков (первые два канала дают практически совпадающие изображения, очень похожи и третий с чётвёртым каналом). Хотя некоторые каналы начали формировать новые признаки (углы квадратов и разные точки на окружности) Таким образом, 8 каналов в финале работы сети для этого датасета избыточны, а 2 чуть маловато.

Интерпретировать работу нейронной сети для конкретного примера можно при помощи SHAP диаграмм (SHAPley Additive exPlanations). С их помощью можно анализировать какие пиксели исходного изображения привели к повышению вероятности данного класса (крастные точки), а какие - к её уменьшению (синие точки).

Стоит понимать, что SHAP отмечает именно те области, которые были выбраны данной моделью в качестве финальных признаков. Естественно, то что для окружности нужны её дуги под 45 градусов, не означает, что для окружности они важны :) Другая модель может выделить другие признаки и картинки SHAP поменяются.

Минимизируем архитектуру

Вернёмся к исходной архитектуре с двумя слоями и двумя каналами в каждом из них. Если уменьшить число каналов во втором слое до одного, результат обучения уже получается не очень хорошим. Это ещё раз подчёркивает, что признаков мало не бывает (до разумных пределов). Однако можно до одного уменьшить число каналов в первом слое:

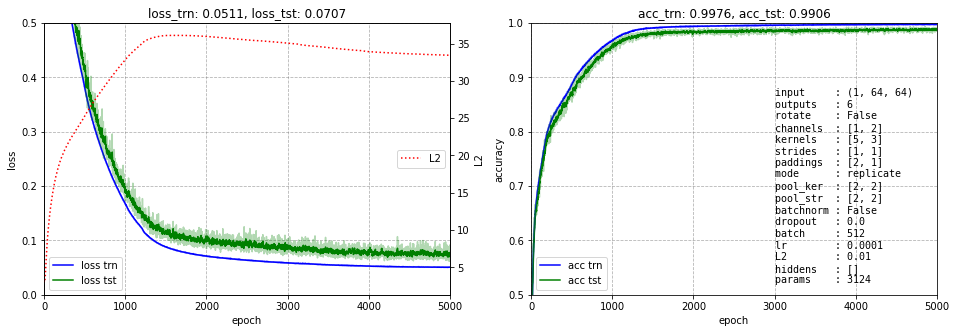
Карта признаков для этой сети выглядит следующим образом:

Заметим, что сеть начинает ошибаться на маленьких фигурах. Ниже приведены все 29 ошибок которые она сделала на 2400 тестовых данных:

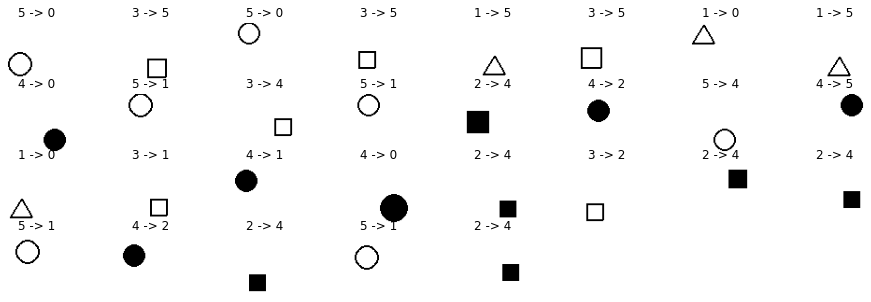
Дополнительную информацию несёт и матрица ошибок (confusion matrix). Сеть почти не путает между собой контурные и залитые фигуры. Больше всего ошибается, принимая залитый квадрат (маленький) за залитый круг (что и не удивительно): 

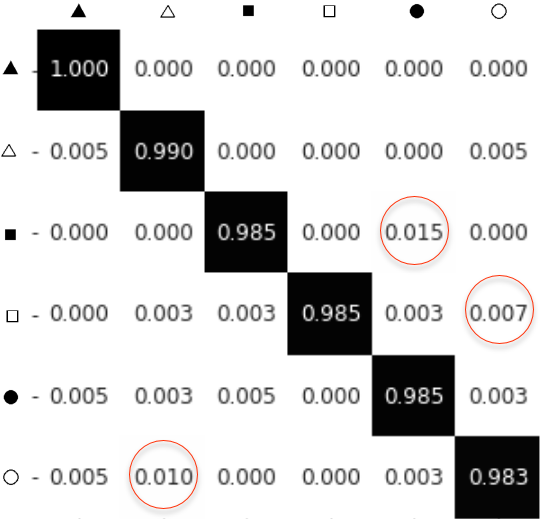
    total accuracy:    0.988
    classes accuracy: [1. 0.99  0.985 0.985 0.985 0.9825]

Ниже приведены также диаграммы SHAP важности пикселей. По вертикали расположены анализируемые примеры, а по горизонтали влияние пикселей на выход каждого из 6 классов:

Добавим вращения

CNN инвариантна относительно небольших сдвигов благодаря слою MaxPool (в пределах ядра пулинга выбирается максимальное значение, положение которого может быть любым). Однако она не инвариантна отсносительно вращений. Поэтому для получения устойчивых к варщению результатов необходимо применять аугментацию (случайно вращать датасет при обучении).

В нашем случае аугментация не потребуется и мы сразу сгененим датасет со случайно повёрнутыми фигурами (и для обучения и для тестирования). Ниже прведены некоторые примеры (размер датасета не изменился):

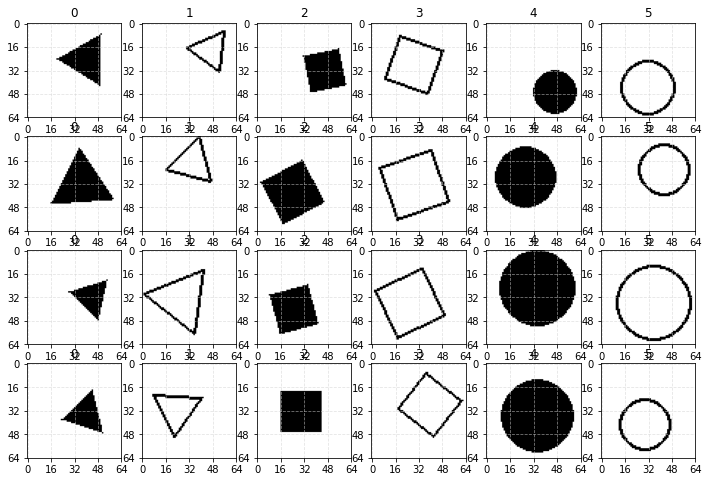
Возьмём варинат "глубокой" сети с четырьмя слоями, но уменьшим число каналов с 8 до 5 для избежания дублирующих карт признаков. Результаты обучения имеют вид (до стабилизации ошибки пришлось учить чуть больше эпох):

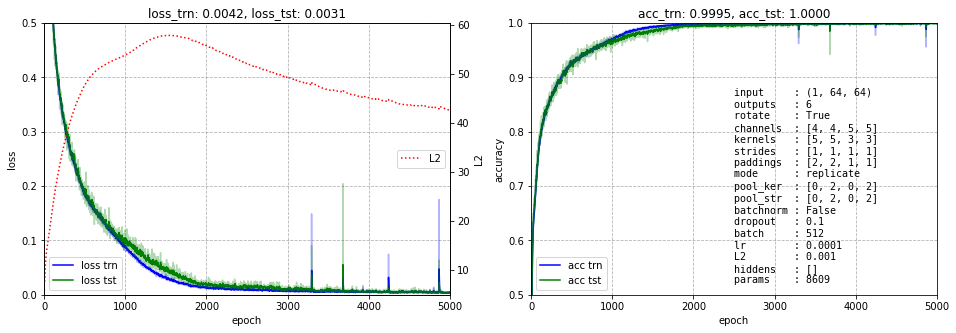
Соответственно пять каналов выходного слоя (на последнем пулинге) имеют такие проекции исходных изображений:

И наконец, SHAP диаграммы:

MNSIT

Перейдём теперь к датасету MNSIT. Он содержит 60k тренировочных и 10k тестовых изображений рукописных цифр от 0 до 9. Изображения имеют 28x28=784 пикселей. Все цифры отцентрированы и яркость изображений нормированная. Ниже приведены некоторые примеры из датасета (белый цвет, как и раньше, имеет нулевое значение):

Линейная модель имеет ошибку порядка 7%, что на самом деле достаточно удивительно:

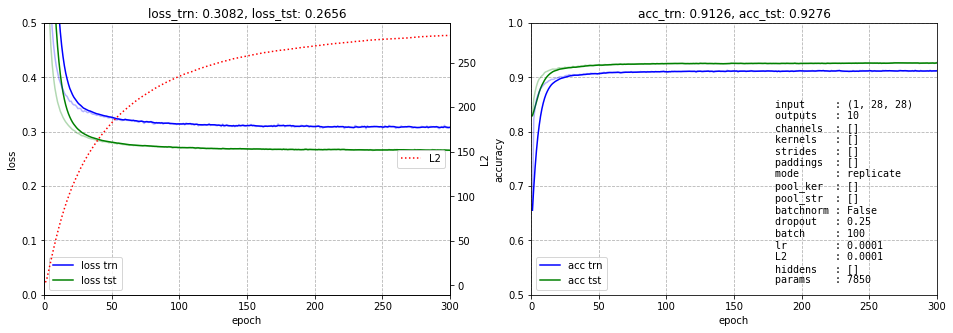
Один скрытый слой её уменьшает до 1.3%, однако ценой 800k параметров:

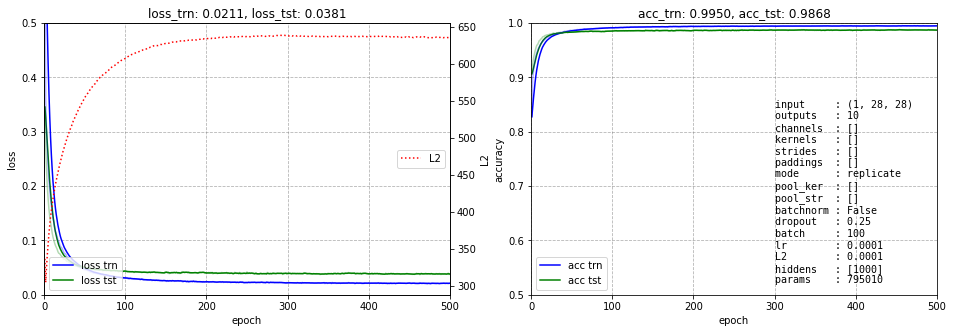
Заметим, что для качественного обучения этой сети не нужно сильно бороться с перевозбуждением нейронов и лучше ослабить L2-регуляризацию. Слой dropout также будет не лишним. Естественно, когда классов много, метрика суммарной аккуратности может оказаться ни о чём. Поэтому приведём аккуратность каждого класса: 

classes:   0     1      2     3     4     5      6     7      8     9
accuracy: [0.993 0.994  0.986 0.986 0.987 0.989  0.989 0.984  0.987 0.980 ]
total accuracy: 0.988

Как видно, нули и единицы распознаются лучше всего. Наибольшие проблемы у девятки.

Заметим, что соревнование за самую низкую ошибку в данном датасете занятие не очень почтенное. Во-первых в нём есть примеры над которыми иногда пасует естественный интеллект (особенно девятки американцам трудно даются, которые они рисуют как четвёрки :). Ниже приведены некоторые примеры ошибок полносвязной нейронной сети (первая цифра класс в дастасете, а вторая - класс к которому этот пример отнесла нейронная сеть):

Во-вторых, сеть с большим числом параметров норовит заняться скрытым переобучением. С одной стороны у нас есть датасет с большим числом различных примеров (70000), который "честно" разбит на тренировочное и тестовое множества (можно и валидационное выделить). Однако различны ли эти примеры в обоих множествах? На одну цифру приходится 7000 вариантов. Попробуйте столько раз различным образом написать, например, единицу :) Можно конечно уменьшить число данных и заняться их агументацией, но уже снова другая история...

Впрочем люди изобретательны. Текущий рекорд ошибки равен 0.17%. Кроме свёрточных нейронных сетей, при этом используются различные методы предобработки изображений, ансамбли моделей и прочие приёмы. Мы не будем всем этим заниматься.

Наша цель иная - посмотреть как нейронная сеть занимается выделением признаков. Сначала убедимся, что свёрточная сеть позволяет получить приемлемую ошибку (ниже эта ошибка равна 0.6%). При этом используется два свёрточных слоя, затем пулинг и ещё два свёрточных слоя. Число каналов достаточно велико (на финальном слое 64). Конечная карта признаков имеет размерность 64x14x14:

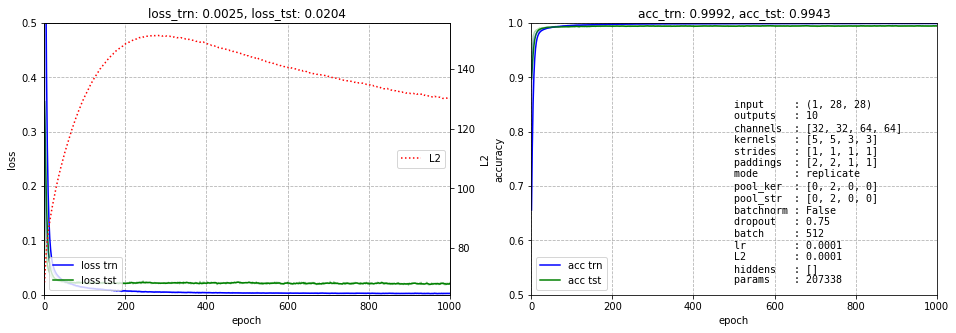
Так как хочется понять как свёрочная нейронная сеть выделяет признаки, чуть пожертвуем точностью, но уменьшим число выходных каналов карт признаков (к слову с двумя каналами сеть не учится, три - минимальное количество):

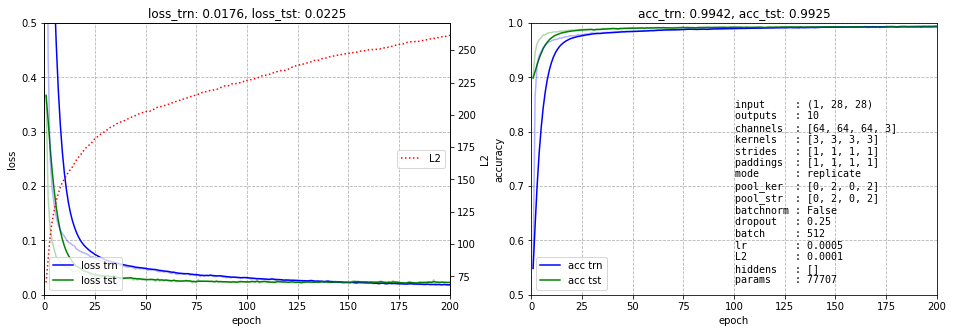
Методы интерпретации CNN

Анализ чувствительности

Анализ чувствительности (sensitivity analysis) вычисляет наиболее значимые градиенты по исходным пикселям от выхода модели: $$ R_i(\mathbf{x})=\left(\frac{\partial f}{\partial x_i}\right)^2 $$ Чем чувствительнее выход модели к конкретным пискелям, тем краснее они на тепловой карте:

Разложение в ряд Тейлора

Разложение в ряд Тейлора (Simple Taylor decomposition):

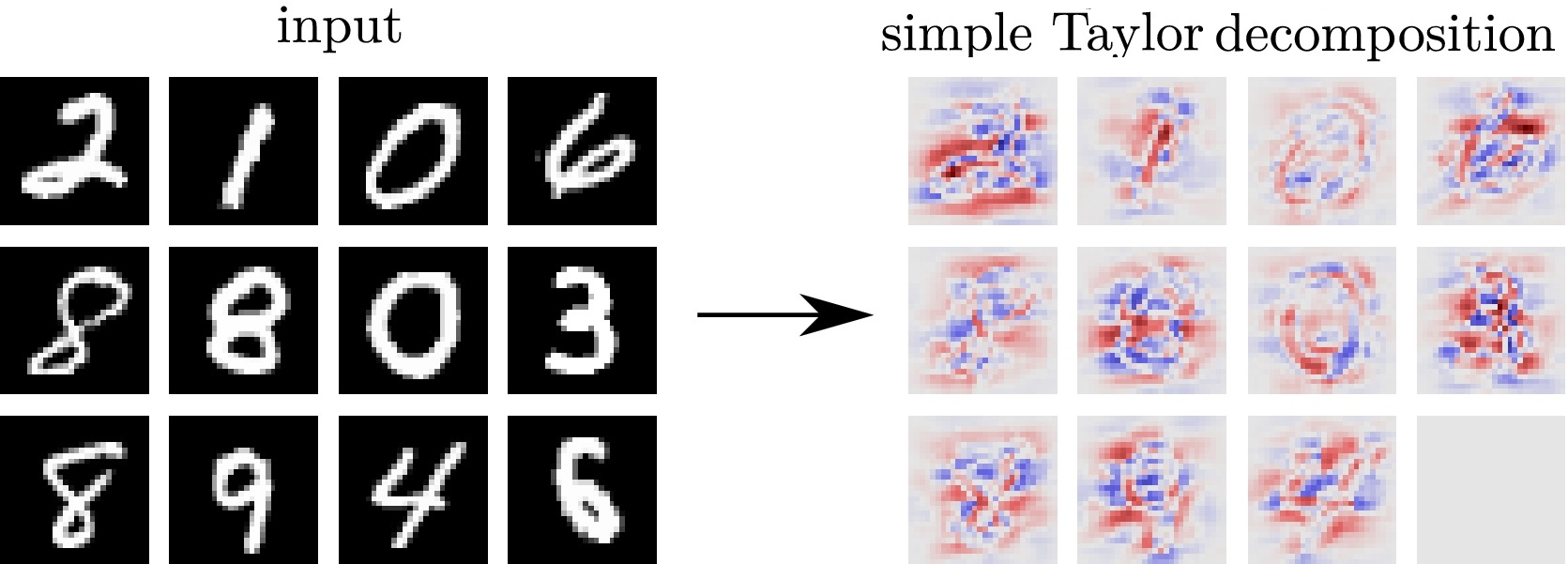
Послойное распространение релевантности (LRP)

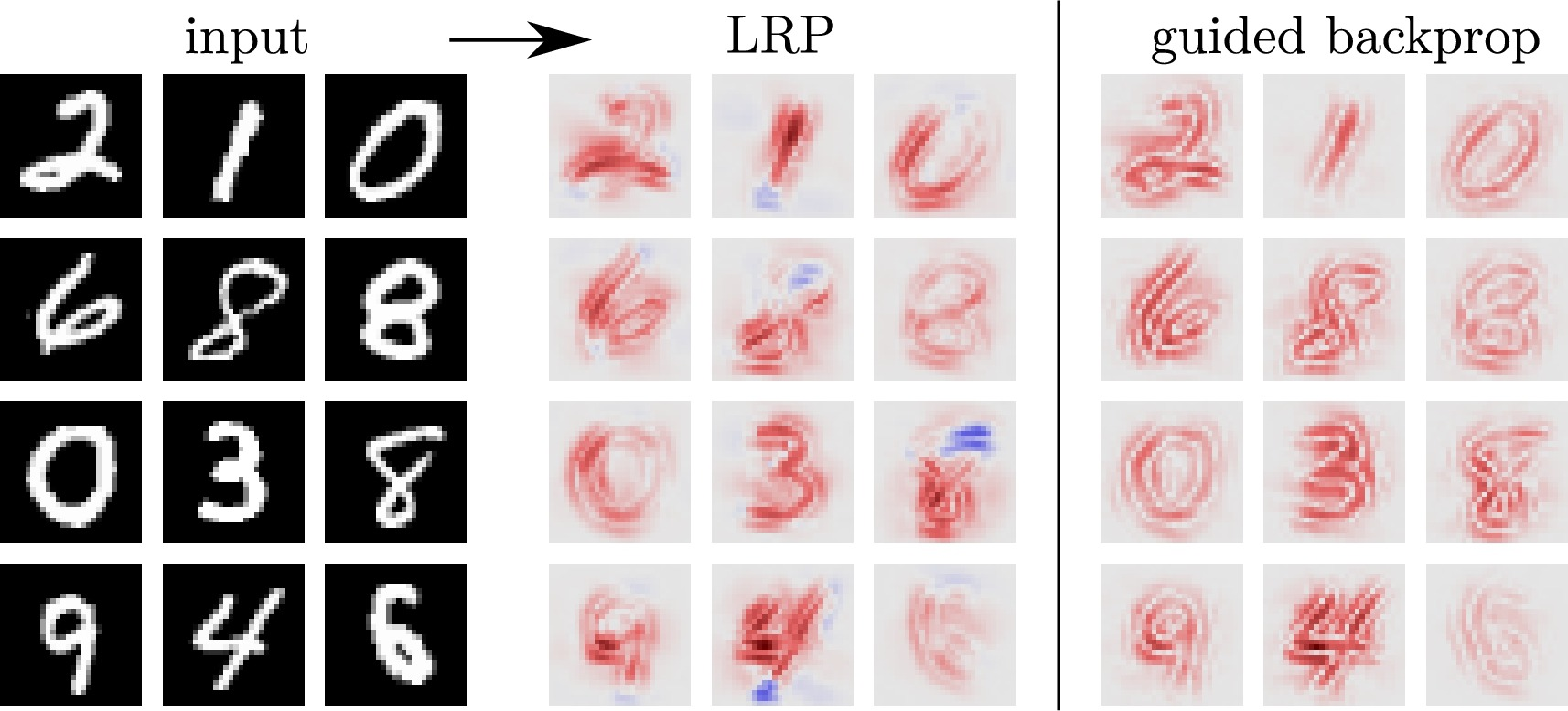
К сожалению, эти подходы (как и SHAP диаграмма) указывают, какие пиксели делают цифру более или менее принадлежащей целевому классу, а не то, что делает цифру принадлежащей этому классу (какие высокоуровневые признаки строит сеть).

Литература