Введение в CNN сети

Введение

В этом документе рассмотрены основные принципы работы свёрточных (коволюционных) сетей. Обычно их применяют для классификации и сегментации изображений. Однако возможны и другие применения, например, при обработке сигналов или текстов.

Фильтры изображений

Свёрточный или конволюционный слой Conv2d является небольшим фильтром, который скользит по изображению, преобразуя его в новое изображение (того же или меньшего размера). Ниже приведены результаты работы чётырёх фильтров 3x3 над верхним изображением:

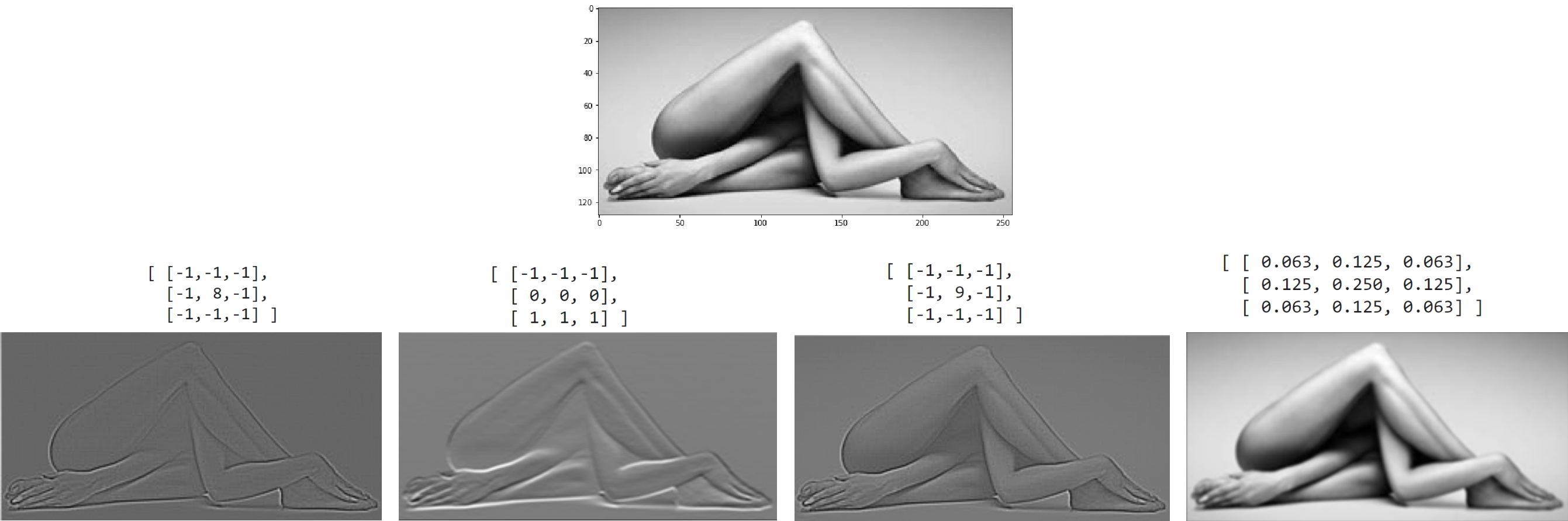
Справа представлена анимация работы фильтра. Пиксели исходного изображения нарисованы синим цветом. Элементы матрицы фильтра - жёлтыми. Чтобы результирующее изображение получилось того же размера, что и исходное, последнее окружается рамкой пикселей (серый цвет), например с нулевыми значениями (это называется паддинг, детали см. ниже).

При получении нового изображения происходит умножение чисел фильтра на значения яркости пикселей которые находятся под ним. Все эти произведения суммируются и результат помещается в первый пиксель нового изображения. Затем фильтр смещается вправо и получается следующий пиксель и т.д.

Приведём численный пример работы фильтра, выделяющего вертикальные границы. Пусть исходное изображение представленно в виде четырёх клеток шахматной доски. Окружать изображение рамкой из нулевых пикселей (паддинг) не будем, поэтому результат свёртки с фильтром 3x3 будет на 2 пискселя меньше: $$ \begin{vmatrix} 1 & 1 & \color{blue}{\bf 1} & \color{blue}{\bf 1} & \color{blue}{\bf 0} & 0 & 0 & 0\\ 1 & 1 & \color{blue}{\bf 1} & \color{blue}{\bf 1} & \color{blue}{\bf 0} & 0 & 0 & 0\\ 1 & 1 & \color{blue}{\bf 1} & \color{blue}{\bf 1} & \color{blue}{\bf 0} & 0 & 0 & 0\\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1\\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1\\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1\\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1\\ \end{vmatrix} ~ \otimes ~ \begin{vmatrix} \color{red}{\bf 1} & \color{red}{\bf 0} & \color{red}{\bf -1} \\ \color{red}{\bf 1} & \color{red}{\bf 0} & \color{red}{\bf -1} \\ \color{red}{\bf 1} & \color{red}{\bf 0} & \color{red}{\bf -1} \\ \end{vmatrix} ~ = ~ \begin{vmatrix} 0 & 0 & \color{green}{\bf +3} & +3 & 0 & 0 \\ 0 & 0 & +3 & +3 & 0 & 0 \\ 0 & 0 & +1 & +1 & 0 & 0 \\ 0 & 0 & -1 & -1 & 0 & 0 \\ 0 & 0 & -3 & -3 & 0 & 0 \\ 0 & 0 & -3 & -3 & 0 & 0 \\ \end{vmatrix} $$ Например, третий пиксель в первой строке результирующей картинке равен (скобками выделены вычисления в каждой строчке фильтра): $(1\cdot 1+1\cdot 0+0\cdot (-1))+(1\cdot 1+1\cdot 0+0\cdot (-1))+(1\cdot 1+1\cdot 0+0\cdot (-1)) = 3$.

Из простых геометрических соображений несложно получить следующую формулу для ширины (и аналогичную для высоты) результирующего изображения: 

width' = int((width + 2*padding - kernel)/stride + 1),

где padding - ширина в пикселях "фейковой" рамки слева и справа от изображения, kernel - ширина ядра и stride шаг с которым он скользит по изображению (на верхнем рисунке stride=1, padding=0, а нижнем stride=2, padding=1 и в обоих случаях kernel=3).

Если stride=1, то чтобы размеры изображения не изменилось для kernel = 3, 5, 7, ..., нужен padding = 1, 2, 3,...

Приведём код на numpy, вычисляющий свёртку (для простоты без падига и с единичным страйдом): 

h, w, k = 8, 8, 3                      # ширина и высота изображения, ядро

img = np.zeros((h, w))                 # image
img[: h//2, : w//2] = 1                # 4 шахматных клетки
img[h//2:,  w//2 :] = 1
res = np.empty((h-k+1, w-k+1))         # результирующее изображение

weight = np.array( [ [1,0,-1], [1,0,-1], [1,0,-1] ] )  # фильтр границы

for i in range(h-k+1):
    for j in range(w-k+1):
        res[i, j] = (weight * img[i: i+k, j: j+k]).sum()

Реализация фильтров на PyTorch

Рассмотрим как вычислять подобные фильтры при помощи библиотеки PyTorch. Импортируем в Python следующие модули: 

import numpy as np
import matplotlib.pyplot as plt
import imageio as imageio
import torch
import torch.nn as nn

Загрузим изображение из файла при помощи библиотеки imageio (получается numpy массив), преобразуем его из трёхканального в одноканальное (при помощи усреднения по всем "цветовым" каналам) и выведем на экран: 

m = imageio.imread("images/yoga.jpg")         # загружаем изображение из файла
print(im.shape)                               # (128, 256, 3) = (высота,ширина,каналов)
im = im.mean(axis=2)                          # усредняем "цветовые" каналы
print(im.shape)                               # (128, 256)

plt.imshow(im, cmap="gray")                   # выводим изображение
plt.show()

Создадим теперь экземпляр свёрточного слоя с одним каналом на входе и одним на выходе (первые два аргумента) и размером фильтра (ядра) 3x3 (третий аргумент): 

conv = nn.Conv2d(1, 1, kernel_size=3, bias=False, padding=1)

Обратим внимание на аргумент bias=False. В общем случае, к сумме произведений элементов ядра на яркости пикселей изображения добавляется смещение (при обчении сети - это параметр). Сейчас мы указываем, что смещения (bias) нам не нужно. Параметр padding=1 означает, что изображение окружается рамкой шириной в один пиксель с нулевыми (по умолчанию) значениями. В результате после применения конволюции, размер изображения не изменится.

Зададим теперь ядро фильтра и поместим его в веса конволюционного слоя. Затем пропустим через него изображение и нарисуем результат: 

kernel = [[-1.,-1.,-1.],                      # фильтр выделения границ
          [-1.,+8.,-1.],
          [-1.,-1.,-1.]] 

im_tensor = torch.tensor(im.reshape( (1,)+im.shape)).float()

with torch.no_grad():       
    conv.weight.copy_( torch.tensor(kernel) ) # задаём веса   
    im1 = conv(im_tensor)                     # пропускаем через слой изображение

plt.imshow(im1.numpy().reshape(im.shape), cmap="gray")
plt.show()

Так как обучения пока нет, при помощи окружения torch.no_grad() мы указываем, что вычислительный граф создавать при прохождении изображения через слой не нужно.

Фильтрация многоканальных изображений

В общем случае фильтр - это 3-мерная матрица. На вход сети поступает изображение, которое обычно имеет один (градации серого) или три (RGB цвета) канала. Конволюционый слой на выходе может иметь произвольное число каналов. Ниже приведен пример, когда на вход слоя поступает два канала, а на выходе получается три:

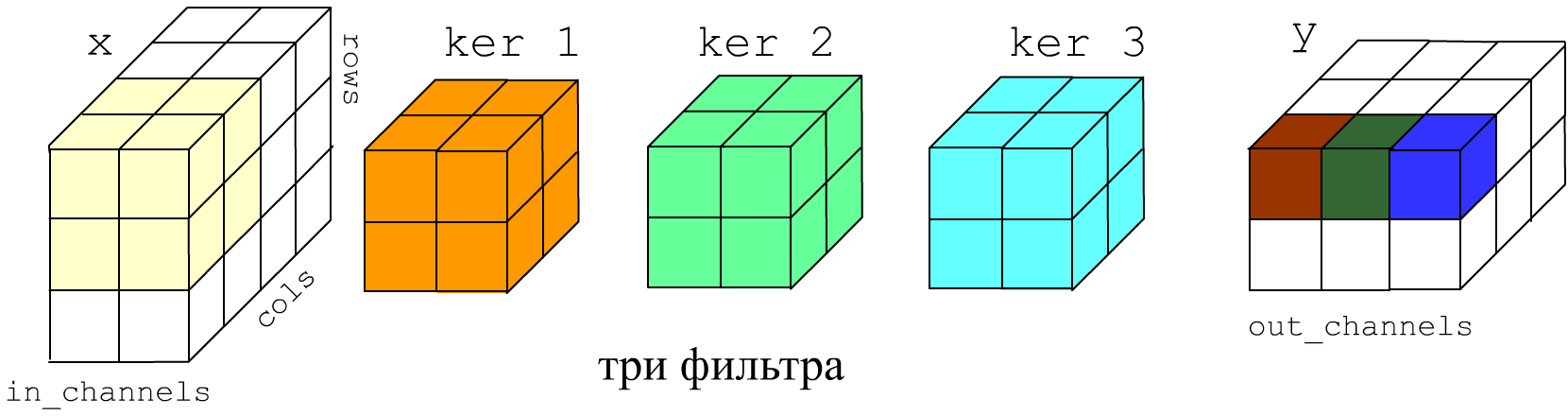
Для каждого выходного канала формируется обучаемая 3D матрица параметров (плюс смещение). Каждая из них независимо и на всю глубину производит вычисление результаты работы такого 3D фильтра.

Таким образом, при создании свёрточного слоя ключевыми параметрами являются число входных каналов (глубина фильтров), число выходных каналов (количество фильтров), размер ядра (ширина и высота фильтров) и шаг stride с которым фильтр скользит по стопке изображений (входных каналов): 

torch.nn.Conv2d(in_channels = 2, out_channels = 3, kernel_size = 2, stride=1, 
                padding = 0, padding_mode='zeros', dilation=1)

Технически важными являются параметр заполнения padding и параметр расширения dilation:

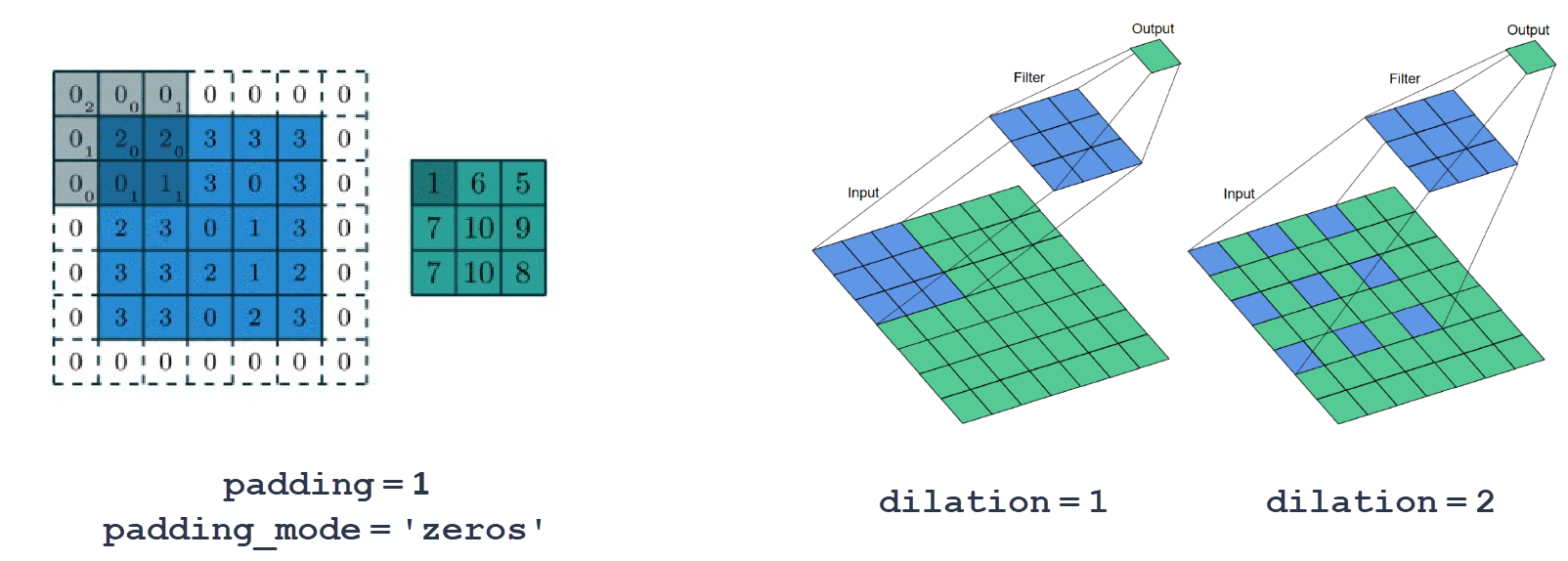
Если мы хотим, чтобы при конволюции размер изображения не менялся, следует окружить его рамкой из "фейковых" пикселей. Для ядра 3 следует взять padding = 1, для ядра 5 - padding = 2 и т.д.

Расширение (dilation) позволяет при том же ядре (и следовательно числе параметров) охватывать большую область изображения. Несмотря на "дырки", если фильтр скользит по изображению с единичным шагом (stride=1), в выходные каналы попадёт информация от всех пикселей входных каналов.

Пулинг

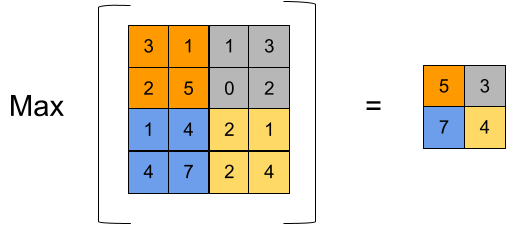Второй ключевой составляющей конволюционных сетей является слой max pooling. Он вычисляет максимальное значение пикселя на входном канале внутри своего ядра: 

torch.nn.MaxPool2d(kernel_size, stride=None, 
                   padding = 0, dilation = 1)
Как и конволюционный слой он имеет размер ядра и шаг. Число каналов на выходе всегда совпадает с числом каналов на входе. При этом максимальное значение вычисляется внутри каждого входного канала независимо. Таким образом, если Conv2d перемешивает все входные каналы, то MaxPool2d этого не делает. Понятно, что этот слой не содержит обучаемых параметров.

Кроме задачи уменьшения размера карты признаков (ширины и высоты стопки каналов), слой MaxPool2d также занимется выделением важных признаков (с максимальным значением). К тому же он делает сеть более устойчивой к небольшим сдвигам изображения (в пределах ядра MaxPool2d).

Реже используется AvgPool2d, который работает аналогично MaxPool2d, но при этом вычисляет среднее значение пикселей данного канала, которые попадают в ядро.

Отметим также AdaptiveAvgPool2d. Он полностью эквиваленте AvgPool2d, но, вместо указания размера ядра, принимает форму желаемого выхода. По полученному входу, он автоматически подбирает необходимое ядро: 

pool = nn.AdaptiveAvgPool2d( (2,3) )
input  = torch.randn(1, 16, 32, 64)
output = pool(input)                    # shape: (1, 16, 2, 3)

Обычно архитектура свёрточной сети содержит цепочку из блоков, состоящих из Conv2d (порождение фильтром новых признаков), ReLU (нелинейность), MaxPool2d (сужение карты признаков). Отметим, что сужение не обязательно делать при помощи слоя MaxPool2d. Если stride фильтра в Conv2d, например, равно 2, то выходные изображения будут в 2 раза меньше, а если не использовать заполнение (padding), то на каждой конволюции будет "откусываться" периметр карты.

Пакетная нормализация

Слой пакетной нормализации BatchNorm2d часто используется в свёрточных сетях (и не только в них). Он вычисляет среднее значение mean и среднеквадратичное отклонение var для каждого канала по батчу данных $x$ и на выходе $y$ нормирует их следующим образом: $$ y = \frac{x-\mathrm{mean}}{\sqrt{\mathrm{var}}}\cdot \mathrm{weight} + \mathrm{bias}. $$ Таким образом, если вход $x$ имеет форму (N,C,H,W), то среднее вычисляется как x.mean((0,2,3)), что даёт C средних для каждого канала (аналогично для var). Обучаемые параметры weight и bias вначале имеют единичное и нулевое значение (для каждого канала). В процессе обучении они меняются, что позволяет сдвигать "нужным образом" среднее значение распространяющихся по сети данных (bias) и их разброс (weight).

Полученные mean и var после каждого батча усредняются скользящим средним и запоминаются (но в обучении не участвуют): 

    running_mean = (1−momentum)*running_mean + momentum*mean,
где по умолчанию momentum = 0.1. Эти средние (как и обученные коэффициенты weight, bias) используются для нормировки данных на этапе тестировании, когда мы указываем model.train(False). Таким образом, даже если через сеть при тестировании проходит батч из одного примера, он будет этой четвёркой отнормирован и в формуле выше вместо mean будет стоять running_mean и аналогично для var.

Выведем параметры слоя BatchNorm2d. Напомним, что в pytorch существует три метода получения информации о параметрах модели. Метод parameters() - это генератор только по обучаемым параметрам (его мы передаём оптимизатору). Метод named_parameters() - аналогичный генератор, но дополнительно содержащий имена параметров. Эти два метода позволяют, в т.ч., достучаться до градиентов параметров. Кроме этого, есть словарь state_dict(), который обычно используется, когда модель сохраняется в файле для последующей загрузки. В нём присутствуют только данные и нет информации о градиентах, однако параметры есть все, включая не обучаемые (в нашем случае running_mean и running_var): 

bn = nn.BatchNorm2d(num_features=3) 

for n, p in bn.state_dict().items():   
    print(f'{n:20s} : {p.numel()} = {tuple(p.shape)}  {p}')
    
for n, p in bn.named_parameters():    
    print(f"{n:10s} : {p.requires_grad}")    

                                 shape   requires_grad   p
    weight               : 3  =  (3,)    True            [1., 1., 1.]
    bias                 : 3  =  (3,)    True            [0., 0., 0.]
    running_mean         : 3  =  (3,)    False           [0., 0., 0.]
    running_var          : 3  =  (3,)    False           [1., 1., 1.]
    num_batches_tracked  : 1  =  ()      False            0

Где встраивать пакетную нормализацию - вопрос интуиции и экспериментов. В полносвязных сетях с несимметричной активационной функцией (ReLU, Sigmoid) её стоит ставить после неё (для устранения смещения). С симметричными функциями (Tanh) - перед (чтобы данные не сильно "срезались" активацией при большой var).

В свёрточных сетях BatchNorm2d, обычно, вставляют сразу после Conv2d, перед несимметричной активацией типа ReLU. В результате, после ReLU, среднее значение будет сдвинуто вверх. Такую же нормировку на положительное среднее значение яркости пикселей делают для входных изображений. Классические значения для RGB каналов: mean=(0.485, 0.456, 0.406), std=(0.229, 0.224, 0.225). Соображения при этом примерноследующие: при использовании паддинга с нулевыми значениями, значимый сигнал нужно приподнять вверх, чтобы снизить влияние границ.

VGG

Приведем пример простой, но достаточно глубокой архитектуры VGG16 которая обучена распознаванию на цветных изображениях 224x224 тысячи классов (машины, кошечки и прочий зоопарк из датасета ImageNet):

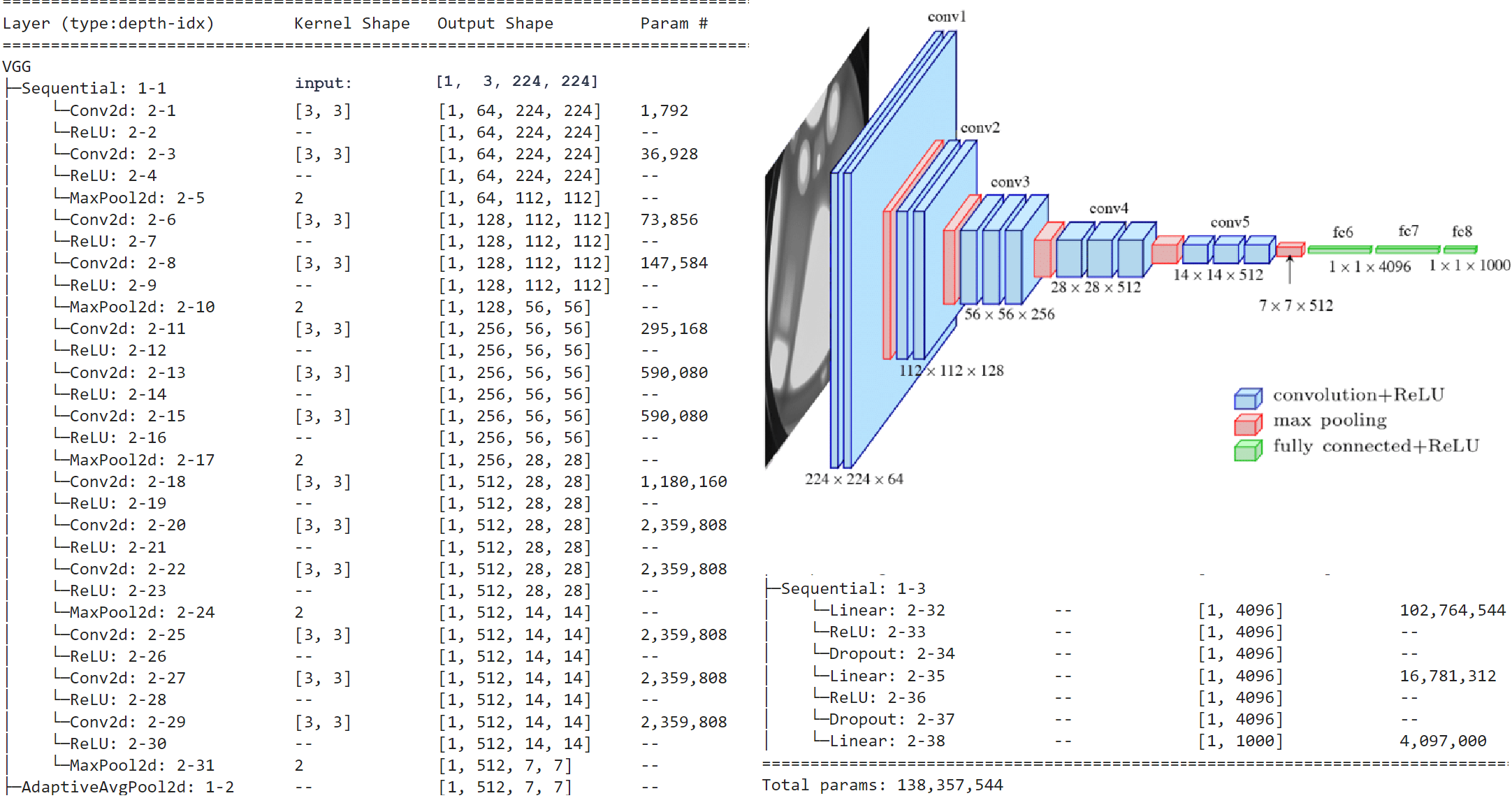
Обратим внимание на сужение и углубление карт признаков по мере удаления от входного изображения. На вход финальной полносвязной решающей сети (которая содержит два дополнительных скрытых слоя), поступает стопка из 512 каналов размера 7x7. Это типичное свойство всех CNN-архитектур (сужаем и углубляем).

Отличительной чертой VGG-архитектуры было введение нескольких, идущих подряд свёрточных слоёв с одинаковым ядром без MaxPool2d между ними (но, конечно, с нелинейностью ReLU). Этим достигается два эффекта. Во-первых две последовательных конволюции расширяют область информации, которая преобразуется фильтром (впрочем этом занимается вся CNN). Так, две 3x3 свёртки по охвату аналогичны одной конволюции 5x5, но содержат меньше параметров. Если C - число каналов, то: 

    (Сin*3*3+1)*Сout + (Сout*3*3+1)*Сout   <   (Сin*5*5+1)*Сout
Но, если Сin << Сout разница небольшая. К тому же основные параметры "наигрываются" на полносвязых слоях (см. выше последнюю колонку в архитектуре VGG), поэтому этот аспект не столь важен.

Важнее то, что между Conv2d стоит нелинейность ReLU. В результате получается аналог двух небольших полносвязных слоёв, которые эффективнее деформируют пространство признаков, чем один больший слой.

ResNet

Сеть ResNet от Microsoft Labs в 2015 году заняла первое место в конкурсе ImageNet. Авторы отмечают, что глубокие стопки свёрточных слоёв приводят к сильному затуханию градиента, а как следствие, к плохой обучаемости. Чтобы решить эту проблему, они ввели "остаточные" (residual) пути по которым градиенту при обратном распространении легче проходить. В результате, даже сети с 1000 слоями достаточно успешно учатся, приводя к дополнительному улучшению точности модели.

Разберём эту архитектуру на примере самой "мелкой" сети ResNet18 из обширного зоопарка сетей ResNet. Исходная ResNet18 работает с изображениями большого разрешения, поэтому на первом конволюционном слое использует ядро 7x7 с шагом 2 и последующим пуллингом с ядром 3 и шагом 2: 

ResNet(
  (conv1):   Conv2d(3, 64, kernel_size=(7,7), stride=(2,2), padding=(3,3), bias=False)
  (bn1):     BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (relu):    ReLU(inplace=True)
  (maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
  ...

В результате, изображение уменьшается в 4 раза по высоте и ширине. Для изображений небольших разрешений эти слои стоит поменять: 

from torchvision import models

model = models.resnet18(pretrained=False, num_classes=10)
model.conv1 = nn.Conv2d(3, 64, kernel_size=(3,3), stride=(1,1), padding=(1,1), bias=False)
model.maxpool = nn.Identity()

Ниже приведена результирующая архитектура ResNet18 (18 слоёв, включая входную конволюцию и классификационный полносвязный слой). Она оптимизирована для входных изображений 32x32 пикселей (например, датасет CIFAR-10):

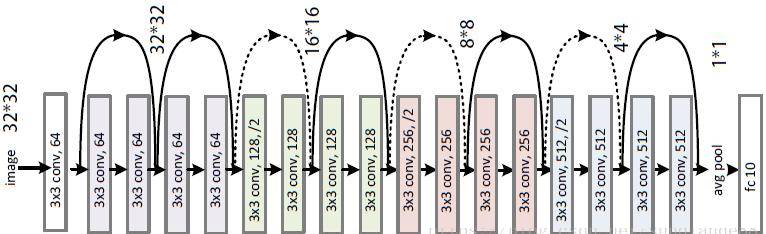
Там, где в блоках стоит 128,/2 и т.д. шаг ядра равен stride=2 (при kernel_size=3, padding=1), т.е. ширина и высота изображения после этого уменьшаются в 2 раза. Обратим внимание, что после уменьшения в два раза размеров карт признаков (каналов) их количество удваивается

Петли на диаграмме отражают структуру двух строительных блоков сети:

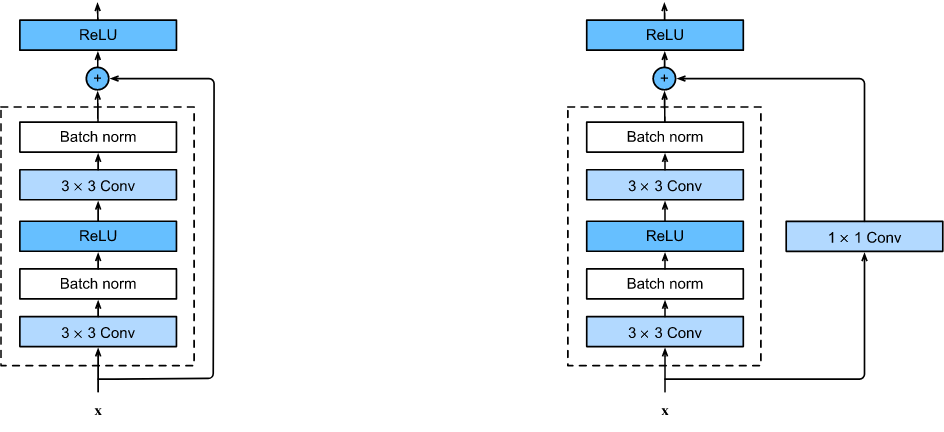
Первый соответствует на архитектурной диаграмме сплошным линиям. К выходу блока, состоящего из двух конволюций, просто подмешивается (суммой) значение входа. Во втором блоке (на диаграмме пунктирные линии) перед смешиванием, вход проходит через конволюцию с kernel_size=1, stride=1. Она умножает вход на обучаемые веса (и перемешивает каналы).

Отметим несколько важных технических моментов:

Google Inception

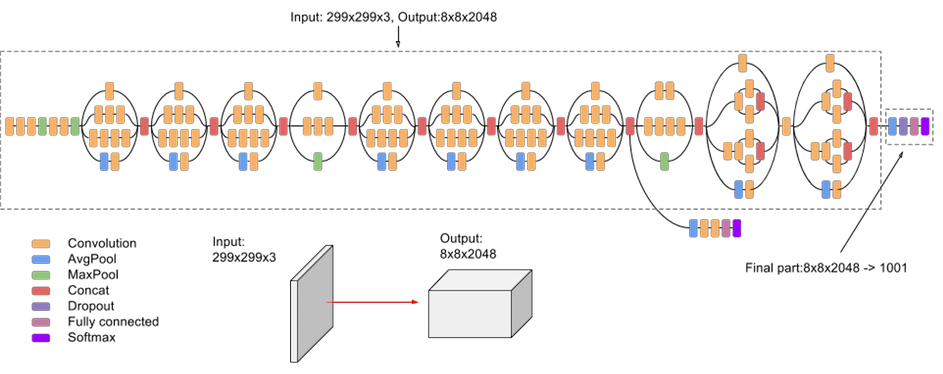
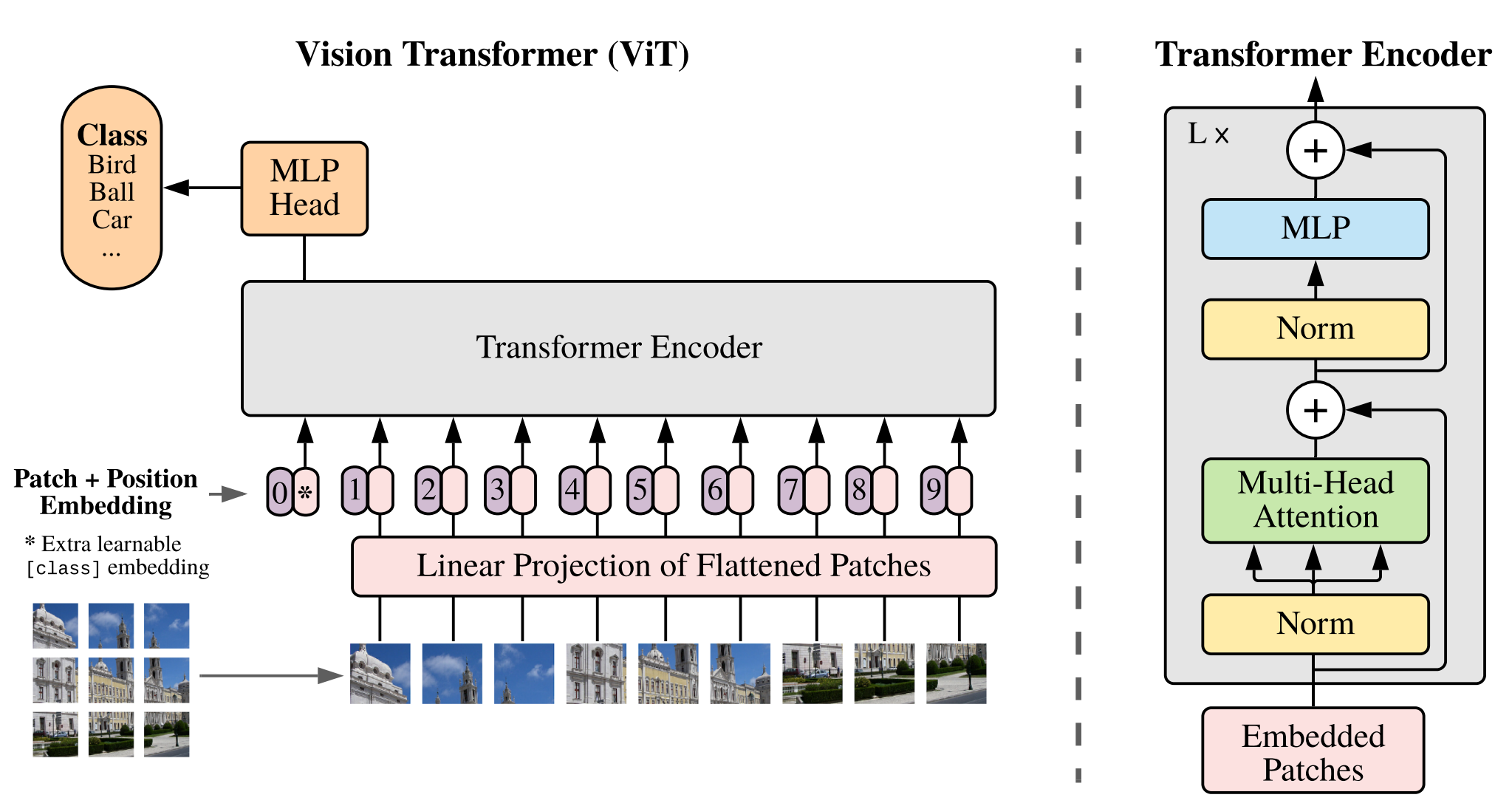
Vision Transformer (ViT)

We split an image into fixed-size patches, linearly embed each of them, add position embeddings, and feed the resulting sequence of vectors to a standard Transformer encoder. In order to perform classification, we use the standard approach of adding an extra learnable “classification token” to the sequence.

CLIP

Contrastive Language-Image Pre-training. В батче находится N пар картинка-текст, которые проходят через ImageEncoder и TextEncoder. Строим матрицу косинусной близости (cosine similarity) между векторами i-й картинки и j-того текста. На диагонали - правильные пары (image, text) - их максимизируем, а остальные минимзируем.

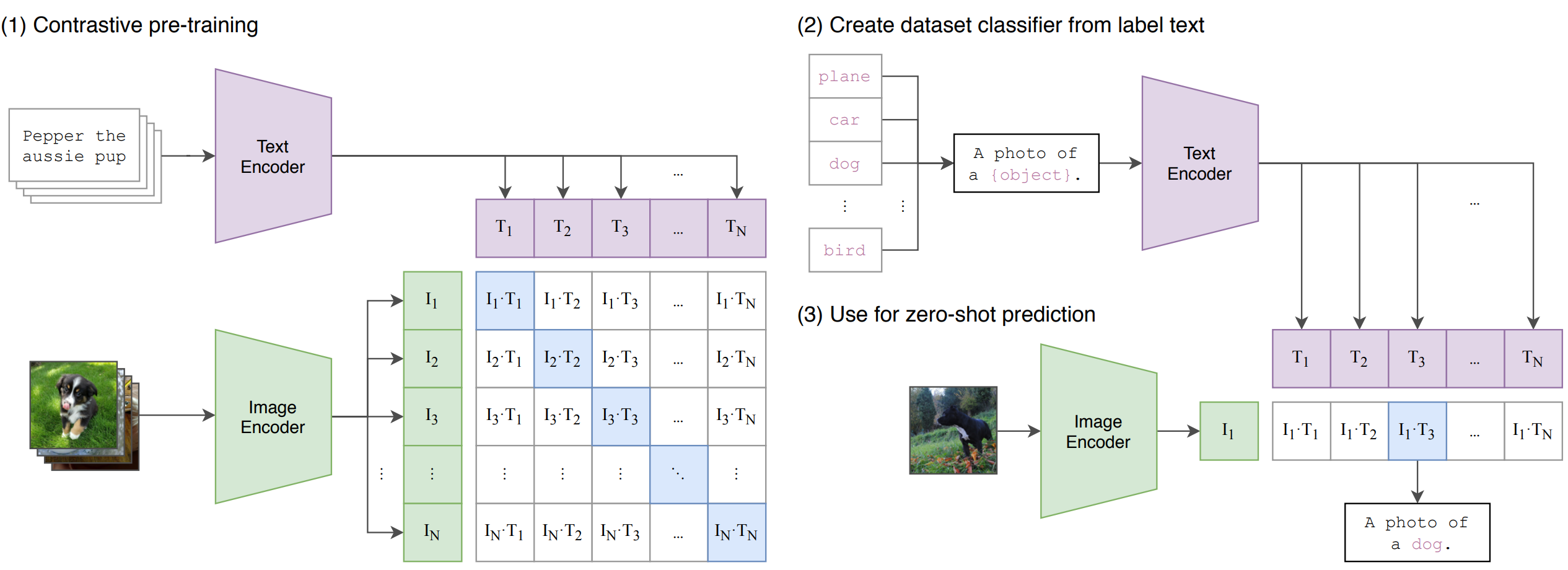
Варианты применения:

Цитаты из статьи (2021):

Литература