ML: Embedding слов

Слой Embedding

Методы эмбединга, основанные на контекстных частотах и PCA-снижении размерности, затруднительно использовать при словарях в несколько сотен тысяч слов. Кроме этого они не позволяют улучшать качество векторизации путём усложения модели. На помощь, как обычно, приходят нейронные сети.

В фреймворках по работе с нейронными сетями существует специальный слой Embedding. Этот слой на вход получает номера слов, а на выходе выдаёт их векторные представления (до начала обучения они случайные):

Выше E = 2 и у слоя три входа (nX = 3). У первого слова номер 0, у второго 2, а у третьего 1. Слой Embedding хранит матрицу формы (V, E), из которой, при подаче на вход числа i, выдаёт i-ю строку.

Векторизацию (= эмбединг = Word2Vec) слов словаря получают разными способами. Например, можно сразу обучать матрицу слоя Embedding непосредственно на своей задаче. Можно также предварительно получить "грубые" значения компонент векторов на упрощённой модели, а затем дообучать на более сложной задаче. Обычно, термины векторизация (или эмбединг) используют в общем случае. Термин Word2Vec более узкий и чаще относится к описываемым ниже методам Skip-gram и CBOW.

Skip-gram и CBOW

Пусть есть длинная последовательность слов (например, естественного языка): $w_0,w_1,...$. Слова близкие по смыслу должны находится в похожем окружении и векторы таких слов должны быть близки.

В Skip-gram в качестве обучающих данных используются пары: данное слово $w_t$ и одно слово из его окружения. Для составления таких упорядоченных пар формируются $(n=2m+1)$-граммы, где $m$ равно числу слов до $w_t$ и после него: $$ \{w_{t-m},...,w_{t-1},\,\underline{w_{t}}\,,w_{t+1},...,w_{t+m}\} ~~~~~~\Rightarrow~~~~~~ \{~ (w_t, w_{t\pm i}),~~~~~i=1...m~\}. $$

Это метод существует в двух вариантах. В варианте Skip-gram Softmax по слову $\mathbf{X} = w_t$ предсказывают одно из слов окружения $w_{t\pm i}$. На выходе сети с V нейронами располагают softmax слой, дающий "условные вероятности": $\mathbf{Y} ~=~ p(w_i| w_t),~~~i=0...V-1$ всех слов в словаре. Функция $\text{argmax}_{i}\,p(w_i|w_t)$ даёт номер $i$ наиболее вероятного слова.

В Skip-gram Negative Sampling оба слова пары $\mathbf{X}=(w_t, w_{t\pm i})$ поступают на вход и относятся к позитивному классу ($Y=1$). Пары $X=(w_t, w')$, где $w'$ - случайное слово текста, относят к негативному классу ($Y=0$). Если словарь достаточно большой, то случайное слово $w'$ скорее всего окажется не из окружения $w_t$. Выбор случайного слова из текста, а не словаря имитирует его правильную частотность. На выходе сети находится единственный нейрон с сигмоидной функцией = [0...1] (бинарная классификация).

CBOW (Continuous Bag of Words) - альтернативный метод Word2Vec, в котором по всем векторам слов, окружающих слово $w_t$, предсказывается его "вероятность" (на выходе размерности V находится функция softmax): $$ \mathbf{X} = [w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m}],~~~~~~~~~~Y = w_{t}. $$

Ниже мы рассмотрим примеры архитектур этих методов. Считается, что Skip-gram лучше работает для редких слов (т.к. они не "прячутся" при усреднении SBOW). Хотя при этом SBOW лучше использует контекст для предсказания слова.

Как и в случае с вероятностным методом, рассмотренным выше, эти методы группируют вместе семантически схожие понятия. Рассмотрим, например, названия дней недели ("Monday", "Tuesday",..., "Sunday"). Они редко встречаются рядом в одном предложении, однако находятся в схожих контекстах: "on Monday morning", "every Monday", "It was a Monday", "one Monday", где на месте Monday может находиться любой день недели. В результате, все дни недели, поворачивая свои векторы в сторону векторов контекста, стремятся притянуться к общей области векторного пространства, куда "ведет суммарная сила" от контексных слов.

Пары слов для Skip-gram метода

Пары pairs для метода Skip-gram будем составлять из слов, попавших в симметричное окно WIN вокруг центрального слова в списке words внутри предложения: 
def get_pairs(words, WIN, pairs):
    for i1, w1 in enumerate(words):               
        if not w1 in word_to_id: continue
    
        i2_beg = max(0, i1-WIN)
        for i2 in range(i2_beg, min(len(words), i1+WIN+1) ):  # вокруг  w1            
            if i2 != i1 and words[i2] in word_to_id:
               pairs.append((w1, words[i2]))
Например после предложения "['the', 'cat', 'likes', 'the', 'mat']" для окна WIN=2 получится такой набор пар: 
('the',   'cat'), ('the',   'likes'), 
('cat',   'the'), ('cat',   'likes'), ('cat',   'the'), 
('likes', 'the'), ('likes', 'cat'),   ('likes', 'the'), ('likes', 'mat'), ...

Так как предложения в используемом корпусе достаточно короткие, мы возьмём окно WIN большим, считая, что все слова предложения образуют контекст для любого его слова: 

pairs = []                                     # список пар
for doc in docs:                               # по документам
    for sent in doc:                           # по предложениям документа
        get_pairs(sent.split(), 100,  pairs)

Перед построением обучающих примеров, как обычно, пары стоит перемешать: 
import random
random.shuffle(pairs)                          # случайно перемешиваем
В корпусе ROCStories (см. файл 100KStories.zip), при составлении пар внутри предложения для WIN = 100, получается 45'671'880 пар (при словаре в 10'393 слова).

Skip-gram Softmax

В паре $(\mathbf{u},\mathbf{w}_i)$ вектор "центрального" слова $\mathbf{u}$ и вектор контекста $\mathbf{w}_i$ будем считать принадлежащими к различным эмбедингам (т.е. отличаем "центральное" слово от слов из его окружения). Это означает, что $\mathbf{u}$ и $\mathbf{w}$ являются строками различных матриц одинаковой формы (V, E). Степень близости слов характеризуется скалярным произведением векторов $\mathbf{u}\mathbf{w}_i$ (параллельные векторы семантически близкими). Получая на вход модели вектор центрального слова $\mathbf{u}$, на выходе будем предсказывать распределение вероятностей слов его окружения. Для этого используется функция softmax (в знаменателе сумма по всем словам словаря $\mathbf{w}_j$): $$ p_i = \frac{e^{\mathbf{u}\mathbf{w}_i}}{\sum_j e^{\mathbf{u}\mathbf{w}_j}}. $$ Если пара состоит из слов с номерами (i,j), то на вход $\mathbf{X}$ модели будем подавать целое число i (номер слова), а на выходе $\mathbf{Y}$ ожидать вектор p=[0,0,...,0,1,0,..,0], где 1 стоит на j-том месте. С целью экономии памяти, для выхода $Y$ указывается только номер j слова (sparse-кодирование для CrossEntropyLoss в PyTorch): 

X = np.zeros((len(pairs), 1),   dtype=np.int64)
Y = np.zeros((len(pairs)),      dtype=np.int64)    

for i, (u,w) in enumerate(pairs):        
    X[i,0] = wordID[u]["id"]          # индекс входного (центрального) слова
    Y[i]   = wordID[w]["id"]          # индекс предсказываемого слова

Простейшая реализация Skip-gram метода в PyTorch имеет вид: 

E_DIM   =  100                                               # размерность векторов

model = nn.Sequential(                                       # (N,1)   input X
        nn.Embedding(V_DIM, E_DIM, scale_grad_by_freq=True), # (N,1,E)
        nn.Flatten(),                                        # (N,E)
        nn.Linear   (E_DIM, V_DIM, bias=False))              # (N,V)   CrossEntropyLoss

Слой Embedding хранит векторы "центрального" слова и имеет V*E параметров.
Вход $\mathbf{X}$ имеет в форму (N,1), где N - число примеров в батче. После Embedding получится тензор $\mathbf{X}_e:$ (N,1,E). Слой Flatten меняет его размерность на $\mathbf{X}_f:$ (N,E). Параметр scale_grad_by_freq сообщает, что при обучении векторы редких слов в батче надо сдвигать сильнее, чем частых слов. Естественно, при этом размер батча стоит увеличить (например N=512).

Полносвязный слой Linear (без смещения bias) содержит матрицу $\mathbf{W}$ весов формы (V, E) с таким же числом параметров, что и в Embedding. Эта матрица является списком векторов $\mathbf{w}_i$. В линейном слое происходит умножение $\mathbf{X}_f\cdot\mathbf{W}^\top,$ где $\mathbf{W}^\top$ - транспонированная матрица. Так как в каждой строке обучающих данных находится вектор входного слова $\mathbf{u}$, он сворачивается с векторами $\mathbf{w}_i$ и после прохождения через softmax получаются вероятности $p_i$. В PyTorch функция softmax вычисляется внутри ошибки CrossEntropyLoss, поэтому на выходе сети её ставить не надо.

$$ \text{N} \left\{ \phantom{ \begin{array}{} \\ \\ \\ \\ \end{array} } \right. \overbrace{ \underbrace{ \begin{array}{|c|c|c|} \hline u_1 & u_2 & u_3 \\ \hline ~ & ~ & ~ \\ \hline ~ & ~ & ~ \\ \hline ~ & ~ & ~ \\ \hline \end{array} }_ {\mathbf{u}} }^ {\displaystyle\mathrm{E}} ~~~ \cdot ~~~ \text{E}\left\{ \phantom{ \begin{array}{} \\ \\ \\ \end{array} } \right. \overbrace{ \underbrace{ \begin{array}{|c|c|c|c|c|} \hline ~ & ~ & w_{i1} & ~ & ~ \\ \hline ~ & ~ & w_{i2} & ~ & ~ \\ \hline ~ & ~ & w_{i3} & ~ & ~ \\ \hline \end{array} }_ {\mathbf{W}^\top} }^ {\displaystyle\mathrm{V}} ~~~~~~=~~~~~~ \text{N} \left\{ \phantom{ \begin{array}{} \\ \\ \\ \\ \end{array} } \right. \overbrace{ \underbrace{ \begin{array}{|c|c|c|c|c|} \hline ~ & ~ & \mathbf{u}\mathbf{w}_i & ~ & ~\\ \hline ~ & ~ & ~ & ~ & ~\\ \hline ~ & ~ & ~ & ~ & ~\\ \hline ~ & ~ & ~ & ~ & ~\\ \hline \end{array} }_{\mathrm{softmax}~~ \Rightarrow~~ p_i} }^ {\displaystyle\mathrm{V}} $$

Матрица векторов находится в model[0].weight, а матрица выходного слоя в model[2].weight. После окончания обучения, чтобы не потерять информацию, находящуюся в матрице $\mathbf{W}$, можно усреднить векторы из Embedding и матрицы Linear: 

E = model[0].weight                 
W = model[2].weight                 
new_E = 0.5*(E+W)                   # (V, E)

Ошибка для Skip-gram Softmax

Выходом модели должны быть вероятности слов. Поэтому при обучении используется nn.CrossEntropyLoss, которая в PyTorch вычислят от полученных выходов модели функцию softmax. Так, если для $i$-того примера необходимо максимизировать вероятность слова с номером $\hat{y}_i=c$, а выходы модели равны $y_{i\alpha}$, то ошибка (усредняемая по всем примерам батча) равна:

$$ L(y, c) = -\,w_c\,\log\left( \frac{e^{y_{ic}}}{ \sum_\alpha e^{y_{i\alpha}}}\right). $$ Веса $w_\alpha$ (по числу слов) могут усиливать вклад отдельных слов. В нашем случае будем повышать вес более редких слов и понижать вес частых слов.

В качестве весов можно, например, взять отрицательный логарифм вероятности слова $w_\alpha=-\log p(w_\alpha)$ в тексте. Однако, так как у нас есть много небольших документов, воспользуемся мерой IDF (inverse document frequency), равной логарифму обратной доли документов в которых встретилось $i$-тое слово: $$ \mathrm{idf}(w_i)=1+\log\frac{ N_D}{N_i+1}, $$ где $N_D$ - число документов (в ROCStories - историй), а $N_i$ - число документов в которых встретилось слово $w_i$: 

    idf = np.zeros( (V_DIM,), dtype=np.float32)    
    for d in docs:                                         # по документам
        for w in set(  w for s in d for w in s.split()  ): # словарь документа
            if w in wordID:                                # слово из нашего словаря
                idf[wordID[w]["id"]] += 1
                
    idf = ( 1+np.log(len(docs)/(idf+1), dtype=np.float32) )
    weight = idf*(V_DIM/idf.sum())

При создании ошибки модели необходимо передать ей полученные веса: 

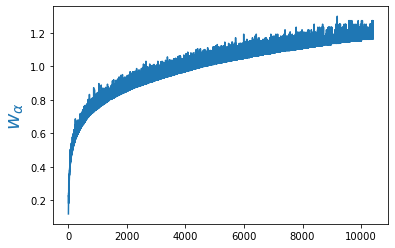
criterion = nn.CrossEntropyLoss(weight = weight)
В результате, например, ошибка слова "the" будет умножаться на 0.12, слова "cat" на 0.62, а "zeus" на 1.27. Выше нарисован график весов, как функция номера слова в словаре.

Веса отнормированы таким образом, чтобы их сумма равнялась числу слов в словаре V_DIM. Это позволяет приблизительно сравнивать ошибку без весов (в которой все веса равны 1) и ошибку с весами. Тем не менее следует помнить, что эти ошибки (даже для одной и той-же модели) будут отличаться. Без весов ошибка обычно меньше, т.к. модели достаточно научиться предсказывать только высокочастотные слова. Например у точки "." pm = 97442, т.е. её вероятность примерно равна 0.1. Достаточно всегда предсказывать точку, чтобы получить аккуратность 0.1.

Обучение Skip-gram Softmax

Одна эпоха обучения со 100 примерами в батче и 45'671'880 общем числе примеров на CPU занимает около полутора часов. Поэтому целесообразно использовать для обучения графический процессор (GPU). 

cpu = torch.device("cpu")  
gpu = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")  

model.to(gpu)
weight = weight.to(gpu)

Соответственно в каждом цикле обучения данные батча также пересылаются в GPU: 
xb = torch.from_numpy( X[it: it+batch_size] ).to(GPU)
yb = torch.from_numpy( Y[it: it+batch_size] ).to(GPU)
       
y = self.model(xb)
Теперь, на одну эпоху тратится около 20 минут.

В случае ROC Stories начальная ошибка, как с весами, так и без них составляет порядка 9.41. Обученная модель с весами имеет loss=7.3, а без весов: 5.3. Такая же ситуауация с точностью (умноженной на веса).

Skip-gram Negative Sampling

Более быстрый вариант называется skip-gram с negative sampling. Чтобы учесть несимметричность пары $[\mathbf{u},\mathbf{v}]$, будем для них использовать различные эмбединг-векторы. Найдём между ними скалярное произведение и пропустим его через сигмоид: $$ p = \frac{1}{1+e^{-\mathbf{u}\cdot\mathbf{v}'}}. $$

Запишем реализацию этой модели на PyTorch в функциональном виде: 
class Skip_gram_Negative1(nn.Module):
    def __init__(self, V_DIM, E_DIM):        
        super(Skip_gram_Negative1, self).__init__()
        
        self.emb1 = nn.Embedding(V_DIM, E_DIM, scale_grad_by_freq=True) 
        self.emb2 = nn.Embedding(V_DIM, E_DIM, scale_grad_by_freq=True) 
        
    def forward(self, x):                            # X из двух колонок
        u  = nn.Flatten() ( self.emb1(x[:,0]) )
        v  = nn.Flatten() ( self.emb2(x[:,1]) )
                        
        dot = u.mul_(v).sum(dim=1)                
        return torch.sigmoid(dot)                    # используй BCELoss

Второй способ учёта "несимметричности" состоит использовании единого эмбединга, с поворотом второго вектора: $\mathbf{v}'=\mathbf{v}\cdot\mathbf{W}$. Для этого он пропускается через обучаемый линейный слой Linear с матрицей $\mathbf{W}$ формы (E, E). Затем вычислим сигмоид от косинуса между векторами: Таким образом, вероятность того, что векторы $\mathbf{u}$ и $\mathbf{v}$ окажутся соседями равна: $$ p = \frac{1}{1+e^{-\mathbf{u}\cdot\mathbf{W}\cdot\mathbf{v}}}. $$ Для векторов $(\mathbf{u},\mathbf{v})$ из одного контекста (параллельных) $p\sim 1$, а для векторов из различных контекстов $p\sim 0$ (оба вектора беруться из одного Embedding). Обучаемая матрица $\mathbf{W}$ играет роль "метрического тензора" при вычислении скалярного произведения. 

class Skip_gram_Negative2(nn.Module):
    def __init__(self, V_DIM, E_DIM):        
        super(Skip_gram_Negative2, self).__init__()
        
        self.emb = nn.Embedding(V_DIM,E_DIM, scale_grad_by_freq=True)
        self.fc  = nn.Linear   (E_DIM, E_DIM)
        
    def forward(self, x):                     
        u  = nn.Flatten() ( self.emb(x[:,0]) )
        v  = nn.Flatten() ( self.emb(x[:,1]) )
        
        dot = (u * self.fc(v)).sum(dim=1)             
        return torch.sigmoid(dot)                    # используй BCELoss

Проблема Skip-gram c softmax в том, что для каждой обучающей пары необходимо вычислять скалярные произведения $\mathbf{u}\mathbf{w}_i$ со всеми словами в словаре. А это довольно долгое мероприятие. Перемножение матриц (N,E).(E,V) = (N,V) и затем вычислениие sum exp (N,V), требует порядка N*V*2*E операций. 

(N,E).(E,V)     -> sum exp (N,V)     

(N,E)*(N,E).sum -> exp (N)           2*N*E

CBOW

В простейшей версии метода CBOW производится усреднение векторов, входящих в модель слов окружения. Результирующий средний вектор пропускается через матрицу линейного слоя Linear с V_DIM нейронами и затем через функцию Softmax (в PyTorch этого делать не надо, если используется ошибка CrossEntropyLoss). При этом вероятности предсказываемого слова равны $p_i = e^{\mathbf{u}\mathbf{w}_i}/\sum_j e^{\mathbf{u}\mathbf{v}_j},$ где $\mathbf{u}$ - средний вектор слов окружения.

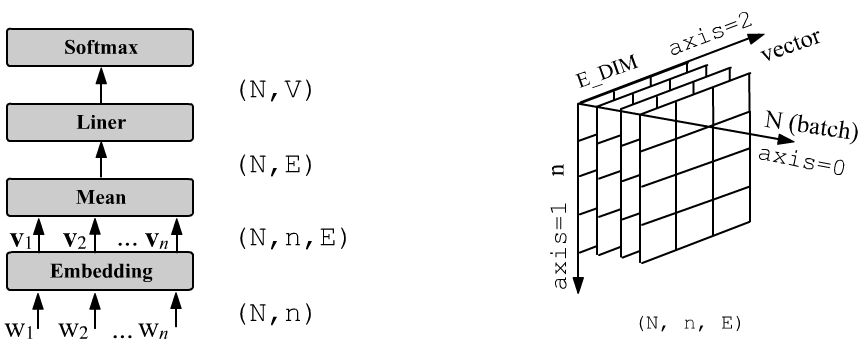
Справа от архитектуры сети нарисована форма тензора после выхода из слоя Embedding. Модель на PyTorch имеет вид: 

class SBOW(nn.Module):
    def __init__(self, V_DIM, E_DIM):        
        super(SBOW, self).__init__()        
        
        self.emb = nn.Embedding(V_DIM,E_DIM, scale_grad_by_freq=True)
        self.fc  = nn.Linear   (E_DIM, V_DIM)
        
    def forward(self, x):              
        x = self.emb(x)
        x = torch.mean(x, dim=1)
        x = self.fc (x)                
        return x                              # используй CrossEntropyLoss

и содержит 2,011,005 параметров (1,000,500 в Embedding и 1,010,505 в Linear). Число слов окружения на число параметров не влияет.

При подготовке данных, для целевого выхода $Y$ каждого примера указывается только номер слова (N, ) (sparse-кодирование) и используется ошибка torch.nn.CrossEntropyLoss().
Соответственно для окна c n = 2*WIN входами также состоят из целых чисел формы (N, n).

Усреднение векторов можно проводить с разными весами и сделать обучаемым. Для этого вместо усреднения вставим скрытый полносвязный слой с HIDDEN выходами и relu-функцией активации: 

import torch.nn.functional as F

class SBOW_Hidden(nn.Module):
    def __init__(self, V_DIM, E_DIM, HIDDEN, INPUTS):        
        super(SBOW_Hidden, self).__init__()
        
        self.emb = nn.Embedding(V_DIM, E_DIM, padding_idx=0, scale_grad_by_freq=True)
        self.fc1  = nn.Linear  (INPUTS*E_DIM, HIDDEN)
        self.fc2  = nn.Linear  (HIDDEN, V_DIM)
        
    def forward(self, x):                     
        x = self.emb(x)
        x = nn.Flatten()(x)        
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc2(x)                
        return x                                # используй CrossEntropyLoss
 
model = SBOW_Hidden(V_DIM, 100, 100, 2*WIN)

Word2Vec и семантические аналогии

Сравнение методов