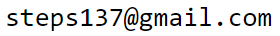ML: Тензоры в Numpy

---

Введение

Нейронная сеть является функцией $\mathbf{T}' = F(\mathbf{T})$, преобразующей один тензор $\mathbf{T}$ в другой $\mathbf{T'}$.
Понимание природы тензоров и операций с ними лежит в основе понимания работы нейронных сетей.

Тензор - это множество упорядоченных чисел (элементов), пронумерованных при помощи d целочисленных индексов: $\mathrm{t}[i_0,\, i_1,\,...,\, i_{d-1}]$. Число индексов d называется размерностью тензора.
Каждый индекс меняется от 0, до $d_i-1$, где $d_i$ называется размерностью индекса.
Перечисление размерностей всех индексов: $(d_0,\,d_1,...,d_{d-1})$ называется формой тензора.

Существующие фреймворки машинного обучения работают с тензорами примерно одинаковым образом.
Ниже мы рассмотрим универсальную библиотеку numpy. Это не справочник по numpy, для этого см. scipy.org.
Мы сосредоточимся на понятиях размерности и формы тензора, а также на том, как они изменяются при различных операциях (что собственно и требуется при анализе нейронных сетей).

---

Размерность и форма тензора

В библиотеке numpy у каждого тензора t есть четыре базовых свойства (атрибута):

Если тензор имеет один индекс: t[i] - то это вектор (ndim=1), а если у него два индекса: t[i,j] - то это матрица (ndim=2). Индексы нумеруются начиная с нуля.

Метод np.array(lst) преобразует список lst (список чисел или список других списков) в тензор numpy:

Обратим внимание, что:

• форма одномерного тензора (вектора) это (n,) , а не (n) , т.к. для Python (n) - это число, а не кортеж.
• t = np.array( [[[1]]] ) - это тензор из одного числа, с shape=(1,1,1) и t.ndim==3, t[0,0,0]==1.

Тензоры принято изображать в табличной форме: вектор (ndim=1) - это строка чисел, матрица формы (rows,cols) - это прямоугольная таблица с rows строчками и cols колонками. Трёхмерный тензор (три индекса, ndim=3) изображают в виде стопки матриц:

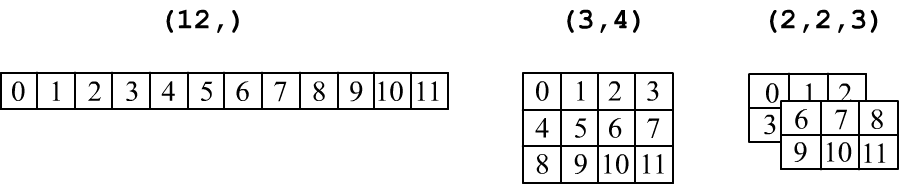
Важно не путать вектор (n,) и матрицу, состоящую из одной строки (1,n) или одной колонки (n,1):

Ниже матрицы из одной строчки или одной колонки окружены двойной линией, чтобы отличить их от вектора:

$$\begin{array}{|c|c|} \hline 1 & 2\\ \hline \end{array} ~~~~~~~~~ \begin{array}{|c|} \hline \begin{array}{|c|c|} \hline 1 & 2\\ \hline \end{array} \\ \hline \end{array} ~~~~~~~~~ \begin{array}{|c|} \hline \begin{array}{|c|} \hline 1 \\ \hline 2\\ \hline \end{array} \\ \hline \end{array}$$

---

Последовательность элементов

Тензор формы shape = (a,b,c) состоит из size = a*b*c упорядоченных чисел (элементов).
Форму тензора можно изменить (с сохранением количества элементов size) при помощи метода reshape или прямого изменения атрибута shape:

$$\begin{array}{|c|c|c|c|c|c|} \hline 1 & 2 & 3 & 4 & 5 & 6 \\ \hline \end{array} ~~~~~~~~\Rightarrow ~~~~~~~~ \begin{array}{|c|} \hline \begin{array}{|c|c|c|c|c|c|} \hline 1 & 2 & 3 & 4 & 5 & 6 \\ \hline \end{array}\\ \hline \end{array} ~~~~~~~~\Rightarrow ~~~~~~~~ \begin{array}{|c|c|c|} \hline 1 & 2 & 3 \\ \hline 4 & 5 & 6 \\ \hline \end{array}$$

При изменении формы тензора методом reshape, результат возвращается по ссылке (не создаётся новой копии множества чисел). Поэтому, если поменять значение элемента в m16, то он поменяется и в v:

Элементы в памяти идут в порядке увеличения индексов, начиная с конца. Например, для трёхмерного тензора с формой (2,1,3) это 6 чисел в следующем порядке:

Менять форму тензора можно произвольным образом, сохраняя неизменным число элементов. Ниже метод arange создаёт вектор (одномерный тензор) из 12 целых чисел от 0 до 11. Затем получаются ссылки на матрицу и трёхмерный тензор. В последнем случае значение -1 в размерности первого индекса, просит numpy самостоятельно высчитать эту размерность (исходя из числа элементов и размерностей остальных индексов):

---

Оси тензора

Индексы - это оси (axis) тензора. Первый индекс - это axis=0, второй axis=1 и т.д. У многих методов есть параметр axis. Например, суммирование по данной оси уменьшает размерность ndim на 1.

Аналогично работают функции min, max, mean, median, var, std, argmin, argmax и т.п.

Из тензора можно вырезать подмножество его элементов. Ниже вырезается нулевая строчка и нулевая колонка, а затем квадратная матрица 2x2:

Подмножества элементов, находящиеся в v1, v2, v3 получаются по по ссылке, а не по значению, поэтому:

Менять можно не только значение одного элемента, но и всех элементов (ниже, стоящих в первой колонке):

---

Сложение, умножение и broadcasting

При поэлементном сложении и умножении тензоров одинаковой формы результат имеет ту же форму: $$(x+y)_{ijk}:~~x_{ijk}+y_{ijk},~~~~~~~~~~~~~~~~~~ (x*y)_{ijk}:~~x_{ijk}*y_{ijk}.$$ Например (ниже np.arange(beg=0, end) - вектор целых чисел от beg до end, исключая end):

Аналогично работают функции от тензоров : $T'_{ijk}=F(T_{ijk})$. Например: np.exp( ), np.log( ), np.sin( ), np.tanh( ), полный список см. на scipy.org.

При добавлении к матрице (n, m) вектора (n,) или матрицы, состоящей из одной строки (1,n), у последней дублируются строки и затем происходит сложение (или умножение) матриц одинаковой формы. При добавлении к матрице (n, m) матрицы, состоящей из одной колонки (m,1), у последней дублируются колонки: $$\begin{array}{|c|c|} \hline 0 & 1 \\ \hline 2 & 3 \\ \hline \end{array} ~+~ \begin{array}{|c|c|} \hline \mathbf{4} & \mathbf{5} \\ \hline \end{array} ~=~ \begin{array}{|c|c|} \hline 0 & 1 \\ \hline 2 & 3 \\ \hline \end{array} ~+~ \begin{array}{|c|c|} \hline \mathbf{4} & \mathbf{5} \\ \hline \mathbf{4} & \mathbf{5} \\ \hline \end{array}, ~~~~~~~~~~~~~~~~ \begin{array}{|c|c|} \hline 0 & 1 \\ \hline 2 & 3 \\ \hline \end{array} ~+~ \begin{array}{|c|} \hline \begin{array}{|c|} \hline \mathbf{4} \\ \hline \mathbf{5} \\ \hline \end{array} \\ \hline \end{array} ~=~ \begin{array}{|c|c|} \hline 0 & 1 \\ \hline 2 & 3 \\ \hline \end{array} ~+~ \begin{array}{|c|c|} \hline \mathbf{4} & \mathbf{4} \\ \hline \mathbf{5} & \mathbf{5} \\ \hline \end{array}$$

Например: В общем случае, для тензоров с различными shape, работает алгоритм расширения (broadcasting):

• выравнивается число индексов (ndim), добавляя к меньшему в shape спереди единицы;
• размерности индексов считаются сравнимыми если они равны или один из них 1;
• размерность единичного индекса увеличиваем до большего, дублируя значения по этой оси:

Например, сложим матрицу из одной колонки и вектора $(3,1) + (2,) = (3,1) + (\underline{1,}2) = (3,2)$: $$\begin{array}{|c|} \hline \begin{array}{|c|} \hline 1\\ \hline 2\\ \hline 3\\ \hline \end{array} \\ \hline \end{array} ~+~ \begin{array}{|c|c|} \hline 4 & 5 \\ \hline \end{array} ~~ = ~~ \begin{array}{|c|} \hline \begin{array}{|c|} \hline 1\\ \hline 2\\ \hline 3\\ \hline \end{array} \\ \hline \end{array} ~+~ \begin{array}{|c|} \hline \begin{array}{|c|c|} \hline 4 & 5 \\ \hline \end{array} \\ \hline \end{array} ~~ = ~~ \begin{array}{|c|c|} \hline 1 & 1 \\ \hline 2 & 2 \\ \hline 3 & 3 \\ \hline \end{array} ~+~ \begin{array}{|c|c|} \hline 4 & 5 \\ \hline 4 & 5 \\ \hline 4 & 5 \\ \hline \end{array} ~=~ \begin{array}{|c|c|} \hline 5 & 6 \\ \hline 6 & 7 \\ \hline 7 & 8 \\ \hline \end{array}$$

---

Свёртка векторов и матриц

Важными операциями являются скалярное произведение векторов и умножение матриц со свёрткой: $$\mathbf{v}\mathbf{u} = \sum^{n-1}_{\alpha=0} v_\alpha\,u_\alpha = u_0\, v_0+...+u_{n-1}\,v_{n-1},~~~~~~~~~~(\mathbf{P}\cdot \mathbf{Q})_{ij} = \sum^{n-1}_{\alpha = 0} P_{i\alpha}\,Q_{\alpha\,j}.$$

В numpy обе операции выполняются при помощи метода dot. Так, для векторов:

Для матриц:

Представим последнее умножение в табличном виде:

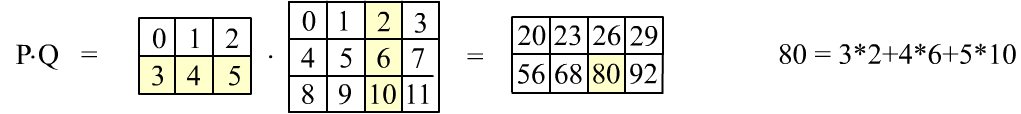
При матричном умножении сворачиваются строки первой матрицы со столбцами второй.
На рисунке выше приведено вычисление элемента $80$, закрашенного желтым цветом.
Чтобы получить все элементы, сначала первая строка первой матрицы должна 4 раза свернуться с 4-я колонками второй матрицы. Это даёт первую строку результирующей матрицы. Затем то-же делает вторая строка, что приводит ко второй строке результата.

Если первая матрица состоит из одной строчки, а вторая из одного столбика, то их произведение будет по-прежнему матрицей, но с одним элементом $(1,\,\underline{2})\cdot(\underline{2},\,1)=(1,\,1)$:

$$\begin{array}{|c|} \hline \begin{array}{|c|c|} \hline 1 & 2\\ \hline \end{array} \\ \hline \end{array} ~ \cdot ~ \begin{array}{|c|} \hline \begin{array}{|c|} \hline 3\\ \hline 4\\ \hline \end{array} \\ \hline \end{array} ~ = ~ \begin{array}{|c|} \hline \begin{array}{|c|} \hline 11 \\ \hline \end{array} \\ \hline \end{array}$$

Свёртка по единственному индексу: $(2,\,\underline{1}) \cdot (\underline{1},\,2) = (2,\,2)$ равна попарному перемножению элементов (по тому же правилу "строка на столбец"): $$\begin{array}{|c|} \hline \begin{array}{|c|} \hline 1\\ \hline 2\\ \hline \end{array} \\ \hline \end{array} ~ \cdot ~ \begin{array}{|c|} \hline \begin{array}{|c|c|} \hline 3 & 4\\ \hline \end{array} \\ \hline \end{array} ~ = ~ \begin{array}{|c|c|} \hline 3 & 4 \\ \hline 6 & 8 \\ \hline \end{array} = c_{i1}r_{1j}$$

---

Транспонирование матриц

Операция транспонирования переставляет элементы таким образом, что столбцы и строчки меняются местами. Если форма исходной матрицы была $(n,\,m)$, то у транспонированной она будет $(m,\,n)$:

$$t^T_{ij} = t_{ji},~~~~~~~~~~~~~~~~~~~ \mathrm{transpose}~~ \begin{array}{|c|c|c|} \hline 0 & 1 & 2 \\ \hline 3 & 4 & 5 \\ \hline \end{array} ~ = ~ \begin{array}{|c|c|c|} \hline 0 & 3 \\ \hline 1 & 4 \\ \hline 2 & 5 \\ \hline \end{array}$$

В numpy транспонирование осуществляется методом transpose() или при помощи атрибута .T:

Подчеркнём что транспонирование и перестановка размерностей при помощи reshape приводят к различному порядку элементов:

Транспонирование не создаёт новой матрицы (возвращается ссылка, а не значения). Поэтому:

Не квадратную матрицу можно умножить саму на себя, только предварительно транспонировав её (иначе не выполнится правило совпадение числа колонок и числа строк):

Для тензоров произвольной размерности операция транспонирования переставляет все индексы в противоположном порядке $t^T_{ijk...}=t_{...kji}$:

Как и в случае с матриц, такая перестановка индексов приводит иному порядку элементов, чем просто изменение атрибута shape.

---

Перемножение тензоров со свёрткой

Для произвольных тензоров операция свёртки dot работает по принципу последний индекс с предпоследним: $$(\mathbf{a}\,.\mathbf{b})_{ijkm} = \sum_\alpha a_{ij\underline{\alpha}}\,b_{k\underline{\alpha} m}.$$

Произведение вектора $\mathbf{V}$ и тензора $\mathbf{T}$, независимо от ndim последнего, интерпретируется следующим образом.
У тензора берутся последние два индекса и делаются такие свёртки (второй случай - по принципу "последний с предпоследним"):

$$\mathbf{T}\cdot \mathbf{V} ~~\Rightarrow~~ \sum_\alpha T_{...i\,\underline{\alpha}}\, V_\underline{\alpha},~~~~~~~~~~~ \mathbf{V} \cdot \mathbf{T} ~~\Rightarrow~~ \sum_\alpha V_\underline{\alpha} \,T_{...\,\underline{\alpha} j}.$$

Если у тензора ndim=2 (матрица), то вектор справа превращается в столбик, а слева - в строчку:

$$\begin{array}{|c|c|} \hline 1 & 1 \\ \hline \end{array} \cdot \begin{array}{|c|c|c|} \hline 1 & 1 & 1\\ \hline 1 & 1 & 1\\ \hline \end{array} \cdot \begin{array}{|c|c|c|} \hline 1 \\ \hline 1 \\ \hline 1 \\ \hline \end{array} ~=~ 6$$ В этом случае для форм имеем: $\underline{(2,)\,. (2,3)}\,. (3,) = (3,)\,. (3,) =$ скаляр или $(2,)\,. \underline{(2,3)\,. (3,)} = (2,)\,. (2,) =$ тот же скаляр.

---

Другие операции свёртки

Существует ещё один метод свёртки matmul (и @ - операция для него). Для ndim = 2 результат такой свёртки не отличается от свёртки dot. Различия начинаются при ndim > 2.

В этом случае тензоры интерпретируются как стопки 2D матриц по последним двум индексам.
Эти 2D матрицы перемножаются независимо в каждой "плоскости стопки".
Последние два индекса тензоров фиксируются, а по остальным тензоры расширяются (broadcasting).
Для векторов индекс добавляется, а потом убирается. $$(\overline{1,}\, 2, 3) ~@~ (\overline{3, 2,} \,3, 5) ~~~\Rightarrow~~~ (\overline{1,1,}\, 2, 3) ~@~ (\overline{3, 2,}\,3, 5) ~~~\Rightarrow~~~ (3, 2, 2, \underline{3}) ~@~ (3, 2, \underline{3}, 5) ~~~\Rightarrow~~~ (3, 2, 2, 5)$$ Перемножить $(\mathbf{3},~2,~3)~ @ ~(\mathbf{3,~2},~3,~5)$ нельзя, т.к. они нерасширяемы по "жирным" индексам (по последним двум индексам должно быть матричное умножение и их не трогаем). Как и в dot, размерность последнего индекса первого тензора и предпоследнего второго должны совпадать.

Универсальная свёртка np.tensordot(A, B, axes = (axes_A, axes_B)) проводит свёртку вдоль указанных индексов тензоров A и B:

Если axes = 1, то это стандартное dot - произведение. Если axes = 0, то это прямое произведение $A\otimes B$.

---

Инициализация элементов

Инициализация элементов тензора может быть самой разнообразной. Для следующих методов элементы будут иметь тип float64:

Следующие функции приводят к целочисленным элементам int32: Тип элементов этих тензоров зависит от аргументов методов инициализации:

---

Тип элементов можно менять в процессе инициализации:

---

Случайные тензоры

Случайные одиночные числа: Случайные тензоры типа float64: Случайные тензоры типа int32: Генерация целых чисел от 0 до len(prob)-1 с вероятностями prob:

---

Разные полезности

Пусть надо отобрать элементы, удовлетворяющие условию:

Ещё одна возможность: numpy.where(condition, x[, y]) - из x или y:

---

Пусть есть два массива, элементы которых нужно синхронно перемешать:

---

Для добавления (типа append) массивов друг к другу, необходимо для начального пустого массива определить форму с нулевым первым индексом (для одномерных - не обязательно)

Если финальный размер известен, лучше сразу его выделить и менять значения.

---

Число значащих цифр и другие свойства вывода тензоров на печать задаются методом:

---