ML: Слой Embedding в Keras
Введение
В нейронных сетях существует специальный тип слоя Embedding, который на вход получает номера слов, а на выходе выдаёт их векторные представления (до начала обучения они случайные):

Выше VEC_DIM = 2 и у слоя три входа (inputs = 3). У первого слова номер 0, у второго 2, а у третьего 1. Слой Embedding хранит матрицу формы (DIC_SIZE, VEC_DIM), из которой, при подаче на вход числа i, выдаёт i-ю строку.
Сопровождающий файл: NN_Embedding_Layer.ipynb. Общую теорию векторизации слов можно найти в этом документе. Слой Embedding в библиотеке PyTorch описан здесь.
Embedding в Keras
Как и во многих других слоях библиотеки Keras, при создании слоя Embedding, можно не указывать размер батча (batch_size - число примеров по которым вычисляют ошибку). Обязательно задание числа слов в словаре VOC_SIZE и размерности векторов VEC_DIM (они определяют размерность матрицы векторов). Опционально можно сразу задать и число входов:
VOC_SIZE = 5 # число слов в словаре VEC_DIM = 2 # размерность векторного пространства inputs = 3 # число входов (число целых чисел) m = Sequential() m.add(Embedding(input_dim = VOC_SIZE, output_dim = VEC_DIM, input_length = inputs)
Форма входного и выходного тензоров слоя Embedding выглядят следующим образом:
(batch_size, inputs) => (batch_size, inputs, VEC_DIM)Слой всегда идёт первым, т.к. на его входе находится тензор с целыми числами: [0...VOC_SIZE-1]. Число входов, как и размер батча, можно не указывать (они автоматически определяться по входному тензору):
m = Sequential() m.add(Embedding(VOC_SIZE, VEC_DIM)) # переменное число батчей и входов
Например, ниже batch_size=1 и inputs=1, 2:
print(m.predict([[0]])) # (1,1)=>(1,1,2): [ [[0.01 0.025]] ] print(m.predict([[0,4]])) # (1,2)=>(1,2,2): [ [[0.01 0.025], [0.035 0.012]] ]Анлогично с batch_size=2 (список списков необходимо явно преобразовать в numpy-тензор!):
print(m.predict(np.array([ [1,2], [3,4] ]) ))
input1 input2
[ [[-0.044 0.029], [ 0.01 0.038]] sample1
[[-0.018 -0.045], [ 0.035 0.012]] ] sample2
Матрица векторов
В методе m.layers[0].get_weights(), как обычно, содержится список матриц с параметрами нулевого слоя. В данном случае он состоит из одной матрицы размерности (VOC_SIZE,VEC_DIM):
[[ 0.01 0.025] <= первое слово id = 0 [-0.044 0.029] [ 0.01 0.038] [-0.018 -0.045] [ 0.035 0.012]] <= последнее слово id = VOC_SIZE-1Перед обучением, значениями компонент векторов будут случайные числа, генератор которых задаётся параметром embeddings_initializer (по умолчанию 'uniform': $[-0.05, 0.05]$, см. initializers).
Можно загрузить готовую матрицу компонент векторов (например, обученную на другой задаче). Если необходимо, чтобы она далее не изменялась, надо указать trainable=False:
m = Sequential() m.add( Embedding(VOC_SIZE,VEC_DIM, weights=[embedding_matrix], trainable=False) )
Регуляризация и ограничения
Компоненты векторов слоя Embedding являются обучаемыми параметрами. Для них (как и для любых параметров) можно установить ограничения значений и регуляризационные довески к ошибке.
Параметр embeddings_constraint (None по умолчанию) задаёт ограничения. Например:
m.add(Embedding(100,2, embeddings_constraint = keras.constraints.UnitNorm(axis=1)))будет контролировать, чтобы векторы были единичными.
Параметр embeddings_regularizer (None по умолчанию) делает ограничение на компоненты векторов более мягкими. Для этого к функции ошибки добавляется, например, сумма квадратов компонент, умноженная на небольшую константу (ниже 0.01). Градиентный метод будет одновременно пытаться уменьшить ошибку предсказания модели и величину компонент, тем самым не давая им неконтролировано увеличиваться:
m.add(Embedding(100,2, embeddings_regularizer = keras.regularizers.l2(0.01) ))
Взаимодействие с Dense и RNN
Полносвязный слой Dense связывает синапсы с последней размерностью предыдущего тензора: $\sum_\alpha X_{i...j\alpha}\,W_{\alpha k}=Y_{i...jk}$. На выходе слоя Embedding находится тензор с размерностью не два, а три, формы (batch_size, inputs, VEC_DIM). Поэтому (если векторы необходимо проконкатенировать), при присоединении после Embedding слоя Dense, между ними надо вставить слой Flatten():
m = Sequential() # 5 2 Output shape: Params: m.add(Embedding(VOC_SIZE, VEC_DIM, input_length=3)) # (None,3,2) 5*2 = 10 m.add(Flatten()) # (None,6=2+2+2) 0 m.add(Dense(1)) # (None,1) 3*2+1 = 7Ниже на первом рисунке приведена архитектура этой модели. Число параметров слоя Embedding равно VOC_SIZE*VEC_DIM, а у слоя Dense с одним нейроном (units=1) матрица (inputs*VEC_DIM, 1) и смещение (одно число) приводит к inputs*VEC_DIM + 1 параметрам.
Слой Flatten параметров не имеет. Его задача сделать входящий тензор данных линейным. При этом он не затрагивает нулевую ось батча, т.е. при действии Flatten() на тензор (batch_size, size1,...,sizeN) получается тензор (batch_size, size1*...*sizeN):
t = keras.backend.ones((10, 2, 3, 4, 5)) # (10, 2, 3, 4, 5) print( Flatten()(t).shape ) # (10, 120)
Если снижение размерности Flatten не сделать, то модель:
m = Sequential() # 5 2 Output shape: Params: m.add(Embedding(VOC_SIZE, VEC_DIM, input_length=3)) # (None,3,2) 5*2 = 10 m.add(Dense(1)) # (None,3,1) 2+1 = 3свернёт выходы Embedding слоя и веса слоя Dense c units нейронами следующим образом:
np.dot( (batch_size, inputs, VEC_DIM), (VEC_DIM, units) ) = (batch_size, inputs, units).
Число параметров в слое Dense теперь будет равно VEC_DIM+1. Это означает, что к каждому вектору присоединяется слой с одними и теми же весами. Ниже эта архитектура нарисована в центре:
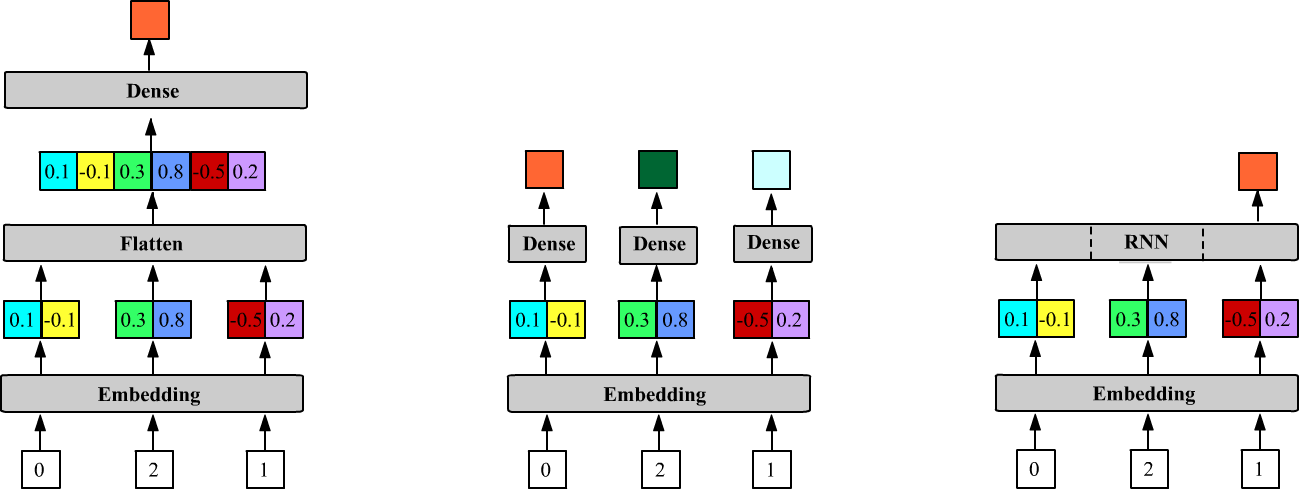
В отличии от слоя Dense, рекуррентные слои ожидают на своих входах векторы, поэтому Embedding к ним присоединяется непосредственно (выше третий рисунок):
m = Sequential() # 5 2 Output shape: Params: m.add(Embedding(VOC_SIZE, 2, input_length = 3)) # (None, 3, 2) 5*2 = 10 m.add(LSTM(1)) # (None, 1) 4*((2+1)+1)=16Рекуррентная сеть (LSTM) по умолчанию имеет return_sequences=False, поэтому выше возвращается скрытое состояние (одномерное) только последней (третей) ячейки.
Маскирование входов
Рекомендуется первое слово в словаре (нулевой индекс) резервировать и не занимать значащим словом. Тогда нулевой индекс можно будет использовать как признак отсутствия входа. Это полезно при переменном числе входов, например в RNN. Для использования маскирования в Embedding надо указать mask_zero=True. Слой по-прежнему будет выдавать векторы по числу входов. Однако последующий RNN слой, вектор с нулевым индексом будет игнорировать, переходя к следующий ячейке:
m = Sequential() m.add( Embedding(VOC_SIZE,VEC_DIM, mask_zero=True) ) m.add( SimpleRNN(1, return_sequences=True) ) print(m.predict(np.array([ [1,0,3,0,2,0,0] ]) )) [[[0.02 ] # вычислили для 1 [0.02 ] # пропустили (0), повторив скрытое состояние для 1 [0.069] # вычислили для 3 [0.069] # пропустили (0), повторив скрытое состояние для 3 [0.065] # вычислили для 2 [0.065] # пропустили (0), повторив скрытое состояние для 2 [0.065]]] # пропустили (0), повторив скрытое состояние для 2
Обычно маскированные входы с нулями идут в конце последовательности, "добивая" короткие предложения до максимальной длины нулями.
Маскирование учитывается также при вычислении ошибки, игнорируя ошибку от маскированных входов.