DemonScript: Пространственные отношения

Введение

Человек, наделённый естественным интеллектом, без труда решит следующую задачу:

Пусть есть три ящика A, B и C. Известно, что ящик A находится в ящике C, а ящик B не находится в ящике C. Находится ли ящик B в ящике A?
Несколько более сложный вопрос: "может ли ящик A находиться в ящике B?" требует уже построения всех моделей, удовлетворяющих условиям задачи. В зависимости от семантики предлога "в" и предположений о закрытости или открытости мира, возможно от двух до шести таких моделей.

Для глубокого понимания естественного языка, компьютер должен уметь создавать модель мира. Собственно, понимание эквивалентно построению адекватной модели, позволяющей отвечать на любые вопросы. Так как получаемая информация всегда неполная, обычно, необходимо перебирать множество различных моделей.
Эти модели приходится упорядочивать по их правдоподобности, используя для этого обыденные знания.

Выбрать правильный формализм для описания модели очень непросто. Пространственная информация может быть, как метрической ("выстою два метра"), так и топологической ("находится рядом", "между ними, но не по прямой"). Временная последовательность событий, обычно, нелинейна и не все существующие объекты известны. Поэтому чисто физические методы не всегда подходят. При наличии множества моделей, непросты также методы проведения логических рассуждений.

В этом документе построена аксиоматика базовых пространственных отношений, соответствующих предлогам "в, на, выше" в условиях неполноты информации.

Отношения

Рассмотрим бинарные отношения, составляющие топологическую основу описания относительного расположения объектов в пространстве:

Данные определения не всегда совпадают с практикой применения аналогичных предлогов в естественном языке. Например, "яблоко в миске" может "выглядывать" за края миски, а "монета на блюдце" - нет. Кроме этого в языке часто не различают отношения in, in# и только при неоходимости добавляют не вполне определённые обороты типа: "непосредственно в" или "где-то внутри". Тем не менее, подобная формализация позволит сформулировать логические правила (аксиомы) понимания интеллектуальной системой взаимосвязи этих отношений.

Примеры

Далее объекты будут изображаются в виде прямоугольников (в двухмерном случае) или параллелепипедов (в трёхмерном), что символизирует некоторые закрытые ящики с крышкой. Это может быть реальный ящик (сундук, шкатулка) или воображаемая граница, окружающая объект. При истинном отношении (X in Y), объект X не может выглядывать из Y. Если один ящик стоит на другом (X on Y), то он стоит на крышке Y и не может "провалиться вниз". Наконец, отношение X above Y ложно, если хотя-бы небольшая часть объекта Х не выше объекта Y.

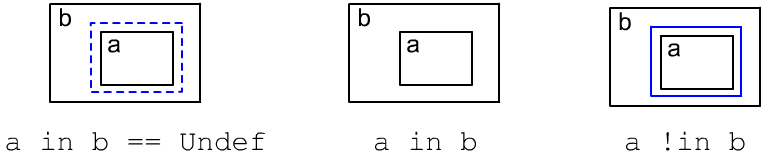
Ниже на двухмерном рисунке приведен пример для отношений in и in# (ящик "a" в ящике "b", "b" в "c" и ящик "d" находится вне всех остальных ящиков). Справа от рисунка записаны некоторые истинные и ложные отношения. Ложное отношение помечается восклицательным знаком "!" у его имени, а запись (a in# b,c) означает пару истинных отношений (a in# b) и (a in# c):

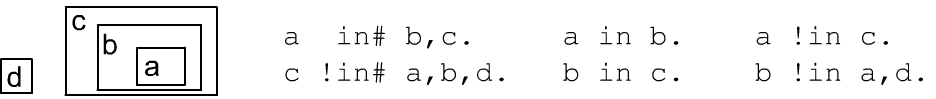
Обратим внимание, что (a in# c) истинно, тогда как (a in c) ложно, что записывается как (a !in c) или
(a in c == False). Действительно, ящик "a" находится не непосредственно в "c", а через вложение в ящик "b".
Аналогичны примеры для отношений above, on:

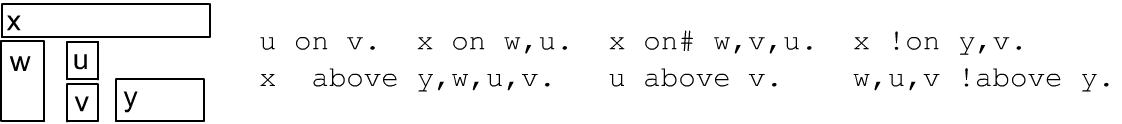
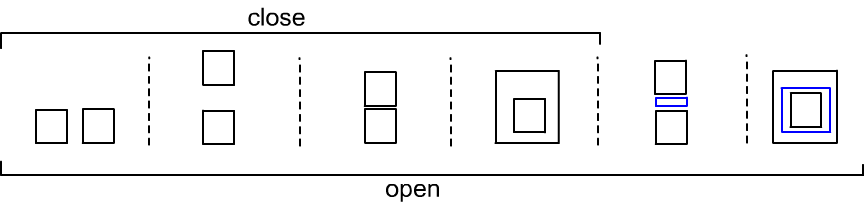
Для закрытых ящиков возможны многочисленные корректные модели в которых то или иное отношение ложно (ниже первые три примера). Однако, существуют двухмерные модели, запрещённые в принципе (таковы последние два примера):

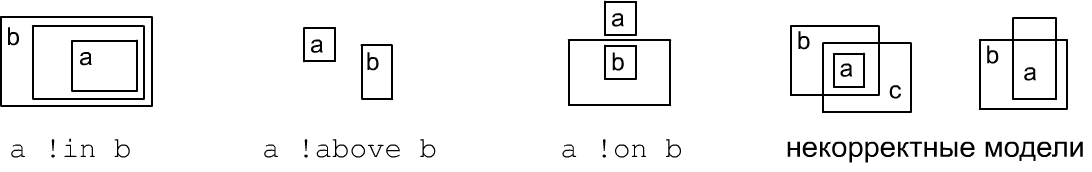
Модель объектов, связанных отношениями in, in#, всегда можно реализовать в двухмерном пространстве при помощи прямоугольников. Для отношений on, on# - ситуация иная. Приведём простейший пример, который имеет смысл только в трехмерном пространстве (параллелепипеды):

True, False и Undef

Задание отношений не всегда однозначно фиксирует модель. Например, пусть есть только три ящика a,b,c и известно, что "b" непосредственно находится в "c" и "a" - выше "b". Эта информация позволяет получить ряд выводов об отношениях между объектами: 

   a !in b.   b !in a.   b !on a,c.   b !above a,c.   c !in a,b.   c !on a,b.   c !above a,b.
Однако не все отношения могут быть вычисленны. Входной информации удовлетворяет пять моделей.
Ящик "a", находящийся выше "b", может быть как в "c", так и не вне его (но выше "b") и т.д.:

Отношения справа от рисунков, в одних моделях истинные, а в других ложные. Поэтому для них используется значение "возможно", обозначаемое как Undef. Истинность такого отношения при данных посылках недоказуема, но не доказуема и его ложность.

Основная задача аксиоматики пространственных отношений состоит в проведении логических выводов когда известны значения True или False только для некоторых отношений. Так как часть отношений в этом случае окажутся неопределёнными (Undef), интеллектуальная система должна уметь, по такой входной информации, строить все (или наиболее правдоподобные) модели.

Прямой логический вывод в подобной трёхзначной логике проводится следующим образом. Все аксиомы записываются в нормальной форме, где атомы соединены дизъюнкцией, например: X !in Y | X in# Y. В качестве переменных X,Y могут стоять любые конкретные объекты (предполагается, что кванторы общности охватывают всю формулу). Пусть, как в примере выше, известно, что b in с истинно. Аксиома всегда истинна, поэтому для X=b, Y=c имеем b !in c | b in# c. Так как первый атом ложен (отрицание), из аксиомы выводится истинность b in# c.

В общем случае, пусть в аксиоме есть n атомов (атом - это отношение или его отрицание). Если n-1 атомов ложны, то оставшийся должен быть истинным. Если же информации недостаточно и значения истинности известно для менее чем n-1 атомов, аксиома не позволяет вывести новое отношение и его значение остаётся неопределённым, т.е. имеет значение Undef.

Открытый и закрытый мир

Мы будем различать открытый и закрытый миры. Мир закрыт, если известны все его объекты. В открытом мире известны только объекты, информация о которых уже поступила на вход интеллектуальной системы. При этом предполагается, что существуют другие объекты, которые могут участвовать в отношениях с уже известными объектами.

Открытый мир не вполне типичен с точки зрения стандартного логического подхода. Например, движок PROLOG основан на закрытости не только объектов, но и отношений (всё, что неизвестно считается ложным). Однако при анализе естественного языка, обычно, приходится проводить рассуждения в условиях открытости мира. Например, фраза "В комнату вошла графиня в очаровательной шляпке", скорее всего не предполагает, что на графине ничего кроме шляпки одето не было.

Пусть в закрытом мире есть два ящика a,b и известно, что (a in# b). Тогда должно быть истинным (a in b).
В открытом мире это не так. Может существовать (не упомянутый пока) ящик "c", для которого выполняется:
(a in c) и (с in b). Поэтому в открытом мире только из (a in# b) нельзя получить значение (a in b), точнее оно равно Undef. На рисунках подобная ситуация будет помечаться пунктиром, означающим "возможно здесь есть один или несколько ящиков". Если отношение между двумя объектами равно Undef (оно не известно и аксиомы его не фиксируют), то возможны две модели (см. рисунок ниже). В одной модели это отношение истинно, а во второй ложно (сплошной линией помечается безымянный и не известный, но точно существующий ящик):

Пунктирное обозначение будет использоваться также и в закрытом мире, если необходимо подчеркнуть, что тут может находиться "что-то ещё из известного" (а может и не находиться). Однако на рисунках моделей такая ситуация возможна, только если нарисованы ещё не все известные объекты.

Аналогичное соглашение принято для отношений on,on#. Если (a on# b) истинно и (a on b)==Undef, это будет изображаться пунктирным ящиком на котором стоит "a", опираясь через него на "b". При поступлении новой информации, может оказаться, что (a on b) истинно и тогда пунктирный ящик исчезнет и "a" "опустится" на "b"

Рассмотрим чуть более сложный пример. Пусть известно, что ящики a,b находятся непосредственно в c. Ящик d находится внутри c, не не непосредственно ("заглянув" в "c" мы его не увидим): 

a, b in c 
d  in# c
d !in  c
В закрытом мире из входной информации следует, что ящик "d" должен находится или в "a" или в "b" (но не в обоих). Это соответствует двум моделям изображённым на первых двух рисунках (пунктир вокруг "d" необходимо опустить). В открытом мире, кроме этих двух моделей есть две модели в которых вокруг "d" существует неизвестный ящик (пунктир заменяем на сплошную линию). Кроме этого, есть пятая модель (последний рисунок). Таким образом, в закрытом мире истинно (d in a) | (d in b), а в открытом мире эта дизъюнкция имеет значение Undef.

Для отношений in, in#, on, on#, above и двух ящиков в закрытом мире возможны четыре неизоморфных расположений ящиков. В открытом мире их шесть:

Рассматриваемая далее аксиоматика не использует информации о размерах ящиков, поэтому они могут быть произвольными (за исключением возможности их вложения in, in#). Выше первая модель соответствует ситуации, когда (X !above Y), так и (Y !above Х), т.е. оба отношения ложны. Поэтому непринципиально какой из ящиков больше или "чуть выше" и они нарисованы одинаковыми, на одном уровне.

Отметим также, что число моделей зависит от числа используемых отношений. Если ограничиться только отношениями in,in#,on,on#, то вторая модель станет неотличимой от первой, а если есть только in,in#, то все три первые модели будут эквивалентными.

Отношения и графы

Ниже на рисунке приведена система вложенных друг в друга ящиков. Если отношение in представить в виде графа, то получится дерево. Поэтому его транзитивное замыкание in# образует строгий древесный порядок.
С учётом транзитивности, в графе отношения in# добавляются ещё рёбра A-E и B-E (второй граф):

Первые два графа приведены в традиционном для математики виде, когда указываются только истинные рёбра, а отсутствие ребра означает ложность отношения. Первый граф отношения in является диаграммой Хассе для отношения in# (в которой не рисуются рёбра транзитивности), а второй - это граф отношения in# на котором указаны все True рёбра. На третьем графе указаны все (как истинные, так и ложные) рёбра отношения in (без подписи его имени). Восклицательный знак рядом с ребром, означает, что соответствующее отношение между парой узлов ложно. Так как мы работаем в терминах трёхзначной логики, отсутствие ребра будет означать не его ложность, а неопределённость Undef логического значения (до поступления соотвествующей информации).

Число возможных неизоморфных моделей для отношений in,in# в закрытом мире соответствует числу деревьев с не помеченными узлами (последовательность A000081). В открытом мире - это деревья в которых рёбра могут быть двух цветов (между родителем и ребёнком есть ящик или его нет). Число таких моделей - это (?) последовательность A005750.

Аксиом, задающих свойства отношений, достаточно много, поэтому необходимо некоторым образом упорядочить процесс их перечисления. Воспользуемся следующей стратегией. Начнем с базового отношения in#. Затем будем добавлять по одному отношению, учитывая только специфичные для него аксиомы, учитывающие также предыдущие отношения.

Аксиоматика отношения in#

Строгий древесный порядок in# обладает следующими четырьмя свойствами:

В DemonScript аксиомы отношения in# запишем следующим образом: 

edges in, in#, on, on#, above, below;             // декларируем отношения

Mind.add
(                                    
   X !in# X,                                      // (1) антирефлексивность    
   Y in# X -> X !in# Y,                           // (2) асимметричность
   X in# Z & Z in# Y -> X in# Y,                  // (3) транзитивность
   Z in# X & Z in# Y -> X in# Y | Y in# X | X==Y  // (4) деревесность
)
В объект Mind, при помощи метода add, добавляются аксиомы. Символ -> обозначает логическое следствие, | - логическое ИЛИ (дизъюнкция), & - логическое И (конъюнкция) и ! - отрицание. Аксиомы предполагаются всегда истинными. Поэтому, в частности, антирефлексивность X !in# X означает, что X in# X ложно.

Все аксиомы находятся под действием квантора общности. Например асимметричность на самом деле имеет вид: ∀X∀Y (Y in# X -> X !in# Y ). Для импликации A -> B мы используем стандартное определение !A | B. Поэтому, каждую аксиому можно записывать в различных видах. Так, формула A -> B эквивалентна !B -> !A, а формула A & B -> C эквивалентна A & !C -> !B.

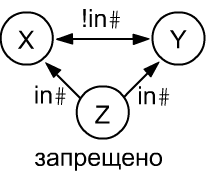Аксиома древесности (4) означает, что Z не может находится одновременно и внутри X, и внутри Y, если они, в свою очередь, не являются вложенными (см. разрешённый пример с ящиками B,C,E на втором графе предыдущего раздела). Эта аксиома включает в себя отношение равенства X==Y. Без него, при совпадающих X и Y, получается неверное утверждение: Z in# X -> X in# X. Равенство X==Y делает в этом случае формулу истинной, независимо от значения остальных её атомов.

Отметим, что из антирефлексивности и транзитивности следует асимметричность: (1),(3) => (2), а из асимметричности следует антирефлексивность: (2) => (1). Вообще говоря, теоремы, следующие из аксиом, можно не добавлять в Mind и, в частности, опустить (2) или (1). Однако мы этого делать не будем. Дело в том, что Mind может работать в режиме в котором переменные с различными именами считаются различными по значению. В этом режиме опускание одной из аксиом приведёт к неполноте аксиоматики отношения.

Аксиоматика отношения in

Мы рассматриваем отношения in и in# равноправным образом. Это означает, что граф вложения ящиков друг в друга может быть частично задан отношением in, а частично отношением in#. Поэтому для in необходима собственная аксиоматика.

Отношение in является транзитивным сокращением для in#, и может быть определено следующим образом: объект X непосредственно находится в Y тогда и только тогда, когда X внутри Y и между ними нет объекта Z внутри которого находится X: 

X in# Y  &  !exists(Z, X in# Z & Z in# Y)  <->  X in Y   // (def1)

Следствие вправо приводит к аксиоме с квантором существования: 

   X in# Y & !exists(Z,   X in# Z & Z in# Y) -> X in Y,     // (ex1)

Следствие влево даёт ещё две аксиомы без квантора существования: 

    X in Y ->  X in# Y,                                 // (5)
    
    X in Y  &  X in# Z  ->  Z !in# Y,                   // (6)
Аксиома (5) - это очевидная связь in и его транзитивного замыания in#. Аксиома (6) приведена на рисунке (если X непосредственно в Y и где-то в Z, то Z не может быть в Y).

Аксиома (ex1) применима только для закрытого мира, где вычислимо значение квантора существования. В открытом мире, если выводить значения истинности отношения только прямым методом, то записанных выше аксиом недостаточно и требуется ещё две формулы: 

   
    X in Y  &  X in# Z  ->  Y in# Z  |  Y == Z,         // (7)

   X in Y  ->  X !in Z | Y == Z,                       // (8) единственность
Свойство "единственности" (8) означает, что ящик не может непосредственно находится в двух различных ящиках. Свойство (7) имеет такую же посылку, как и в аксиоме (6). Обе эти формулы можно доказать от противного. Несложно видеть, что атом с равенством в последних двух формулах необходим, так как, если его не будет, при Z=Y получится в общем случае неверные утверждения.

Пусть, например, (a in# b) и (c !in# b). Тогда в любом мире следует, что (a !in c). Свойство (7) сразу приводит к этому результату. Без (7) приходится применять метод от противного: пусть это не так и (a in c), тогда по (5) имеем (a in# c), что противоречит свойству древесности для отношения in#: 

   (6):   a in  c  &  a in# b   =>   b !in# c
   (4):   a in# b  &  a in# c   =>   b  in# c  |  c in# b   =>    b in# c.

Отметим, также свойства антирефлексивности и асимметричности отношения in: 

   X !in X,                                            // (1')* антирефлексивно
   Y in X  ->  X !in Y,                                // (2')* асимметрично
Они следуют из связи отношений (5) и свойств отношения in# (см. приложение).

Примеры рассуждений для in и in#

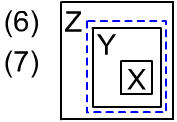
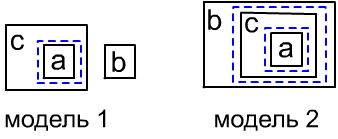Повторим задачу из введения: пусть известно, что ящик "a" находится где-то внутри (in#) ящика "c", ящик "b" не находится внутри "c". Какие выводы можно сделать?
В закрытом мире возможны две модели (на рисунке справа пунктиры необходимо опустить). В одной модели ящик "b" находится вне ящика "c", а в другой ящик "c" находится внутри "b" (и поэтому "b" в "c" не находится). В обоих моделях, в закрытом мире, ящик "a" непосредственно находится в "b", поэтому отношение (a in c) должно быть истинным.

В открытом мире возможно шесть моделей для всех вариантов с пунктиром (его нет или он заменяется на сплошную линию). Значение отношения (a in c) в открытом мире уже не определено. При этом и в открытом, и в закрытом мире b !in# a,c.

Получим решение при помощи DemonScript: 

var G = GRAPH("G")                                // создаём пустой граф
GRAPH = G                                         // делаем его текущим
nodes a,b,c                                       // добавляем в него три узла

a  in# c;                                         // а находится внутри c
b !in# c;                                         // b не находится внутри c

out G                                             // выводим исходный граф
Mind.set_graph(G)                                 // запускаем логический вывод
out G                                             // выводим финальный граф
Исходный граф и граф после проведения логических выводов (метод set_graph) в открытом мире выглядят следующим образом: 
   G { 
      a {  in#: [ c] },
      b {  in#: [!c] },
      c {}           }

   G {
      a{ in#: [!a, c],     in: [!a,!b],    },
      b{ in#: [!a,!b,!c],  in: [!a,!b,!c], },
      c{ in#: [!a,!c],     in: [!a,!c],    } }
В закрытом мире добавляется только одно отношениие a in c. Чтобы запустить вывод в модели закрытого мира, необходимо для графа включить режим GRAPH.close(True). Тогда результат работы функции exists будет бинарным (True, False). Без этого флага функция exists может также возвращать значение Undef.

Напомним, что a {...} - это узел a графа, где в фигурных скобках перечислены все рёбра, которые исходят из узла. Пока у нас есть только два типа рёбер in# и in. После их имён, в квадратных скобках идёт перечисление узлов в которые эти рёбра направлены. Если перед именем узла стоит восклицательный знак, это означает, что данное отношение ложно.

Например, результат (a !in# a) - это сработала аксиома антирефлексивности (1). Более нетривиальный вывод (a !in b) получается при помощи (7) Ещё один важный вывод: (b !in# a) следует из (3). Приведём отладочную информации о процессе логического вывода, которая получается установкой флага Mind.verbose(1): 

   axiom (1): (a in# a) => False :  -> !(a in# a)
   axiom (1): (b in# b) => False :  -> !(b in# b)
   axiom (1): (c in# c) => False :  -> !(c in# c)
   axiom (2): (c in# a) => False :  (a in# c)  -> !(c in# a)
   axiom (3): (b in# a) => False :  (a in# c) & !(b in# c) -> !(b in# a)
   axiom (5): (a in a)  => False : !(a in# a) -> !(a in a)
   axiom (5): (b in a)  => False : !(b in# a) -> !(b in a)
   axiom (5): (b in b)  => False : !(b in# b) -> !(b in b)
   axiom (5): (b in c)  => False : !(b in# c) -> !(b in c)
   axiom (5): (c in a)  => False : !(c in# a) -> !(c in a)
   axiom (5): (c in c)  => False : !(c in# c) -> !(c in c)
   axiom (7): (a in b)  => False :  (a in# c) & (b != c) & !(b in# c) -> !(a in b)

Этот пример можно найти в файле in_on_test_01.ds.

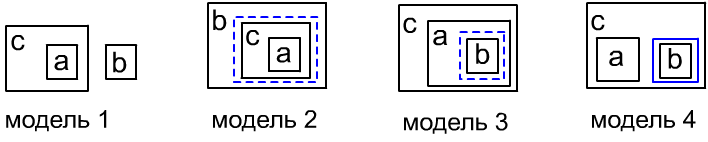
Для аналогичной задачи с отношениями in результат другой и в закрытом мире условиям соответствует уже три модели, а в закрытом - шесть моделей. Для открытого и закрытого миров имеем: 

a  in c;                                          // а находится непосредственно в c
b !in c;                                          // b не находится непосредственно в c


G { 
   a{  in#: [!a, c], in: [!a,!b, c], },
   b{  in#: [!b],    in: [!b],       },
   c{  in#: [!a,!c], in: [!a,!c],   } }

Если дополнительно появляется информация, что (b in# c), то в открытом мире будут возможны только две последние модели. В закрытом мире разрешена только предпоследняя модель. Однако логический движок DemonScript тут не справляется, оставляя неопределённым (b in# a) и соответственно, не срабатывает (ex1), чтобы получить (b in a). В открытом и закрытом мире получается: 

G {
   a{ in#: [!a,!b,c],  in: [!a,!b,c],   }, 
   b{ in#: [!b,c],     in: [!b,!c],     }, 
   c{ in#: [!a,!b,!c], in: [!a,!b,!c],  }}

Связано это с особенностями функции exists, которая только вычисляет значение, но не меняет рёбер: 

   b !in c &  b in# c  => exists(Z, b in# Z & Z in# c) 
   
  = (b in# a & a in# c) | (b in# b & b in# c) | (b in# c & c in# c)
  = (b in# a & a in# c) = b in# a.

При существующем логическом движке, чтобы в закрытом мире сделать правильный вывод, необходимо начать перечислять возможные модели, положив сначала (b in# a), а затем вместо этого (b !in# a). Первый вариант приведёт к третей модели, а второй - в закрытом мире вызовет ошибку на аксиоме (ex1), т.к. эта модель в нём невозможна.

Аксиоматика отношений on, on#

В этой паре отношений, снова начнём с транзитивного замыкания on#. Оно образует строгий, частичный порядок (в отличии от in# без аксиомы древесности): 

   X !on# X,                                      // (11) антирефлексивность    
   X  on# Y -> Y !on# X,                          // (12) асимметричность
   X  on# Z & Z on# Y -> X on# Y,                 // (13) транзитивность

На отношение on# влияет также отношение in#. Ниже приведены две аксиомы, которые обязуют ящики иметь крышку и дно: 

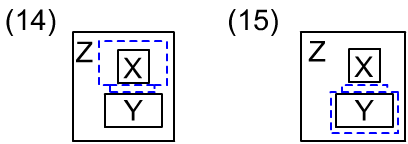
   X on# Y  &  X in# Z   ->   Y in# Z,            // (14)  
   X on# Y  &  Y in# Z   ->   X in# Z,            // (15)
Действительно, если X операется на Y и находится при этом внутри Z, то при наличии дна у ящика Z в нём будет находится и Y. Аналогично для крышки в (15).

Из этих аксиом при Z=Y в (14) и Z=X в (15) следует, что если один объект находится в другом, то они не могут опираться друг на друга (также и наоборот, см КНФ этих аксиом): 

   X in# Y -> X !on# Y,                           // (14')*
   X in# Y -> Y !on# X,                           // (15')*

Отношение on, по аналогии с in, можно определить при помощи квантора существования (X стоит на Y тогда и только тогда, когда он опирается на Y и между ними нет других объектов): 

X on Y    <->    X on# Y  &  !exists(Z,  X on# Z  &  Z on# Y)    // (def2)
Следствие в левую сторону даёт аксиому с квантором существования, применимую только в закрытом мире: 
   X on# Y & !exists(Z, X on# Z  &  Z on# Y)  ->  X on Y,        // (ex2) только Close!
Следствие в правую сторону приводит к очевидной связи (16: если стоит, то и опирается) и менее очевидной (17), которая является следствием транзитивного сокращения (праямой путь X-Y лишний): 
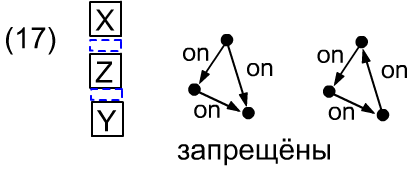
   X on Y -> X on# Y,                             // (16)
    
   X on# Z  &  Z on# Y ->  X !on Y,               // (17)

Отношение on антирефлексивно и асимметрично: 

   X !on X,                                       // (11')* антирефлексивно
   Y on X -> X !on Y,                             // (12')* асимметрично

Как и в случае с in, эти свойства выводимы из предыдущих соотношений. На этом аксиоматика отношений on и on# окончена.

Аксиоматика отношения above

Отношения above образует строгий частичный порядок, без древесного ограничения. Оно антирефлесивно, транзитивно (и, следовательно, асимметрично): 

   X !above X,                                    // (21) антирефлексивно
   X above Y -> Y !above X,                       // (22) асимметрично   
   X above Z & Z above Y -> X above Y,            // (23) транзитивно
Существует также ряд аксиом, связывающих above с остальными отношениями. Так, очевидно, что: 
   X on# Y -> X  above Y,                         // (24)

   X in# Y -> X !above Y,                         // (25)
   Y in# X -> X !above Y,                         // (26)

Справедливо также соотношение, аналогичное по смыслу аксиоме (17): 

   X above Z & Z above Y  ->  X !on Y,            // (27)
Из него и (24) выводимо (17). Однако, для ситуаций, когда отношение above не используется, необходимо сохранить аксиому (17). Кроме этого, для трёх объектов справедливы две разрешающие аксиомы (приводящие к истинности отношения above): 
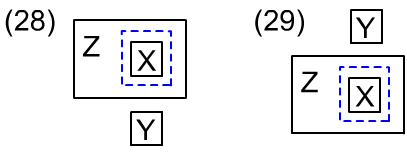
   X in# Z  &  Z above Y  ->  X above Y,          // (28)
   X in# Z  &  Y above Z  ->  Y above X,          // (29)

Аксиоматика отношения below

Для полноты картины добавим также аксиомы для отношения below: 

    Y above X -> X below Y,                        // (31)
    Y below X -> X above Y                         // (32)
Двустороннее следование означает формулу эквивалентности X below Y <-> Y above X.

Тест для всех отношений


nodes a,b,c, d

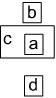
a in c;
b on  c;
d below c;

Mind.set_graph(G)
out G
Результат: 
   a{ in#: [!a, c,!d], in: [!a,!b, c,!d], on: [!a,!b,!c,!d],above: [!a,!c, d],  below: [!a,!c,!d]},
   b{ in#: [!a,!b,!d], in: [!a,!b,!c,!d], on: [!a,!b, c],   above: [!b],        below: [!b],     },
   c{ in#: [!a,!c,!d], in: [!a,!b,!c,!d], on: [!a,!b,!c,],  above: [!a,!c, d],  below: [!a,!c,!d]},
   d{ in#: [!a,!c,!d], in: [!a,!d,!c],    on: [!a,!d],      above: [!a,!c,!d],  below: [ a, c,!d]}

Ящики без крышки

Выше рассматривалась модель ящика с крышкой, на которую можно ставить другие ящики. Эту модель можно расширить на ящики без крышки. Для этого введём граф смыслов Sen в котором будет смысл $lid (крышка). При описании конкретных объектов будем определять есть у ящика крышка или нет: 

   a  has Sen.$lid;           // у ящика "a" есть крышка
   b !has Sen.$lid;           // у ящика "b" нет  крышки

Если у ящика нет крышки, на него нельзя никого поставить: 

   X !has Sen.$lid -> Y !on X.

Часть аксиом не зависит от наличия или отсутствия крышки. Другие истинны, только при наличии соответствующей информации. Например, аксиому (14) следует модифицировать следующим образом: 

   X on# Y  &  X in# Z  & Z has Sen.$lid  ->   Y in# Z,   // (14)

Заключительные замечания

  • Отношение above более общее, чем on# (включает его), отношение on# более общее, чем on, а in# - более общее, чем in. Большая общность означает, что данное отношение выполняется на большем числе моделей. Например X above Y может быть истинно, и когда X on Y ложно, но не наоборот.

    Это выражается следующими аксиомами, каждая из которых записана в трёх эквивалентных формах: 

       X in  Y -> X in#   Y.       X !in#   Y -> X !in  Y.        X !in  Y  |  X in# Y.
   X on  Y -> X on#   Y.       X !on#   Y -> X !on  Y.        X !on  Y  |  X on# Y.
   X on# Y -> X above Y.       X !above Y -> X !on# Y.        X !on# Y  |  X above Y.
    В посылках надо использовать более общие отношения (тогда они будут выполняться и для частных).

    Пусть есть верное утверждение вида (X in Y & ... -> ... ), где в посылке может быть как in так и in#.

    Тогда для формулировки утверждения в виде аксиомы надо использовать in#, а не in.
    Если же в посылке стоит отрицание, то наоборот, используется отношение !in, а не !in#.
    Действительно, если для конкретных объектов известно, что (a in b), то это приведёт к истинности (a in# b) и аксиома с in# сработает для обоих отношений. Если же известна истинность только (a in# b), аксиома также сработает (но только для отношения in#). Аналогично, если истинно (a !in# b), из него выводимо (a !in b).
    В следствии аксиом всё с точностью до наоборот, т.к. A & B -> C эквивалентно A & !C -> !B.

    Всё сказанное справедливо для всех остальных пар, включая пару (on, above), так как справедлива следующая цепочка импликаций: X on Y -> X on# Y -> X above Y. Естественно, обязательно необходимо проверять, что верно верно не только для частного случая, но для более общего.

  • При генеративном порождении значений отношений (применяем аксиомы, пока граф не перестаёт изменяться), необходимо учесть, что если есть аксиома F -> G, то также справедливо и !G -> !F. В объекте Mind это автоматически учитывается, так как все формулы представляются в КНФ. В частности аксиома F -> G имеет вид !F | G. Аналогично, если в посылке два атома, то аксиомы утраиваются. Например: 
          A & B -> C    <=>     !С & B -> ! A       <=>     A & !C -> В.
    Однако все они имеют одинаковую КНФ: !A | !B | С, поэтому достаточно в Mind добавить только одну запись этой аксиомы.

  • Приведенная аксиоматика не учитывает размерности пространства. В большинстве случаев это не критично. Однако иногда может оказаться важным. Например, если ввести отношения слева, справа, спереди, сзади в 2-мерном пространстве (прямоугольники), при помощи 4-х объектов можно "зажать" между ними пятый. В 3-мерном пространстве для этого необходимо ещё два объекта и отношения above, below.

  • Рассмотренные в этом документе аксиомы можно найти в скрипте порождения возможных, топологически различных, моделей: in_on_models_genarator.ds

    Литература

    • Carola EschenbachLars, Lars Kulik - "An Axiomatic Approach to the Spatial Relations Underlying Left - Right and in Front of - Behind"
      (1997) KI-97: Advances in Artificial Intelligence pp 207-218.
      Аксиоматика пространственных отношений на плоскости.
    • AU Frank - "Ontology for spatio-temporal databases" Spatio-temporal databases, 2003 - Springer
    • A. Aho, M. Garey, J. Ullman. - "The Transitive Reduction of a Directed Graph" //
      SIAM Journal on Computing — 1972. — June (vol. 1, no. 2). — P. 131—137.
      Ввели понятие «транзитивное сокращение». Выше это in для in# и on для on#.

    Приложение: Доказательства

    ✒ Покажем, что из антирефлексивности (1) и транзитивности (3) отношения in# следует его асимметричность: (1),(3) => (2). Положим Y=X в аксиоме транзитивности (3) и запишем её в нормальной форме: 
       X !in# Z | Z !in# X | X in# X    =>    X !in# Z | Z !in# X   <=>   X in# Z -> Z !in# X,
    где сначала опущен член X in# X как всегда ложный (по первой аксиоме), а затем нормальная формы снова записана как импликация.

    ✒ Аналогично, показывается, что при Y=X, из асимметричности следует антирефлексивность: (2) => (1): 

       Y in# X -> X !in# Y   =>    X !in# X | X !in# X   <=>  X !in# X.

    ✒ Докажем асимметричность отношения in, формула (2'): Y in X -> X !in Y или Y !in X | X !in Y.
    Прямое использование (5): X !in Y | X in# Y здесь не поможет и необходим метод от противного.
    Если формула выводима из аксиом, то её отрицание должно привести к противоречию. Так как каждую формулу окружают кванторы общности, отрицание приводит к кванторам существования: 

       !∀X∀Y (Y !in X | X !in Y)  <=>   ∃X∃Y (Y in X & X in Y) =>  b in a.  a in b.
    На последнем шаге введены сколемовские константы (два конкретных ящика) "a", "b". Воспользовавшись аксиомой (5), получаем b in# a. a in# b. Это противоречит асимметричности отношения in#, аксиома (2). Полученное противоречие говорит о выводимости (2').

    ✒ Покажем зависимость аксиомы единственности. Взяв её отрицание, имеем: 

    !∀X∀Y∀Z (X in Y -> X !in Z | Y == Z)  <=>  ∃X∃Y∃Z (X in Y & X in Z & Y != Z)  =>  a in b. a in c.

[5]  (a in# b) => True  :  (a in b)  -> (a in# b)
[5]  (a in# c) => True  :  (a in c)  -> (a in# c)
[2]  (b in# a) => False :  (a in# b)  -> !(b in# a)
[2]  (c in# a) => False :  (a in# c)  -> !(c in# a)

[6]  (b in# c) => False :  (a in c)  (a in# b)  -> !(b in# c)
[6]  (c in# b) => False :  (a in b)  (a in# c)  -> !(c in# b)

all atoms False:
(a in# c) & (a in# b) -> (c in# b) | (b in# c)

    Приложение: Примеры





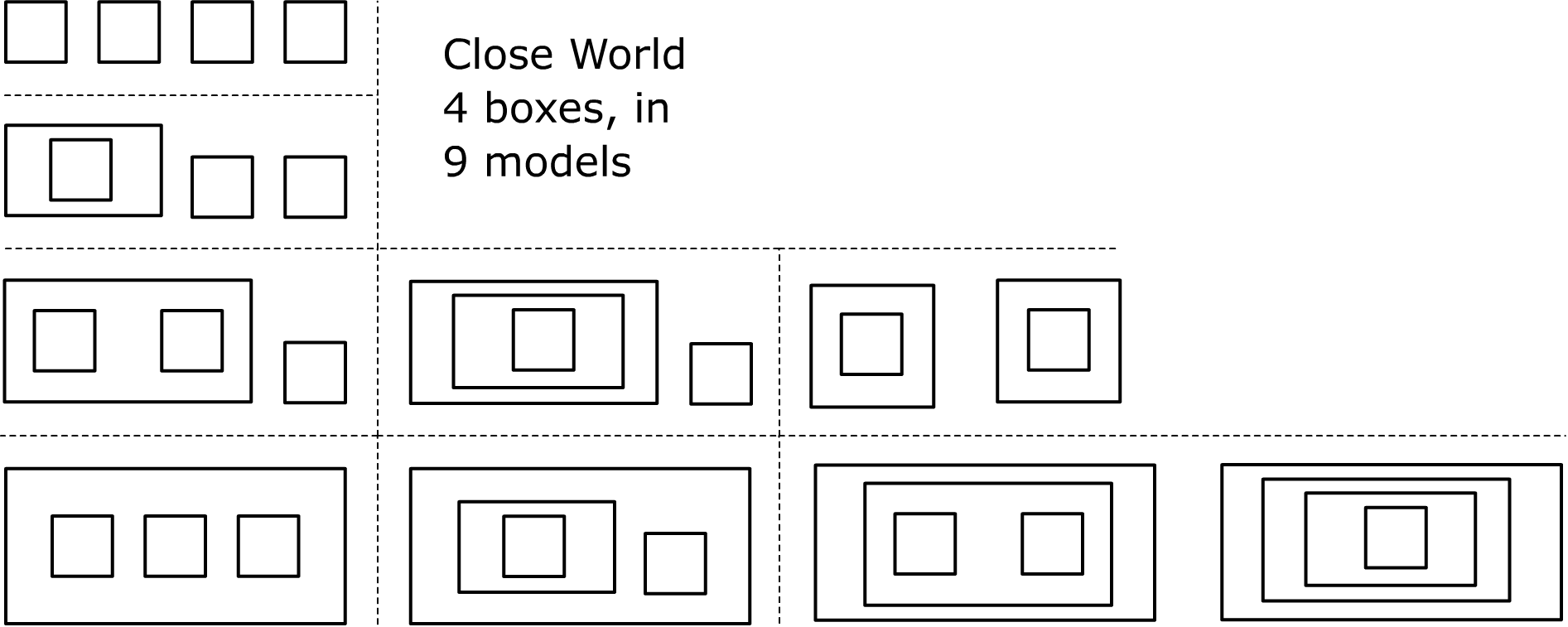
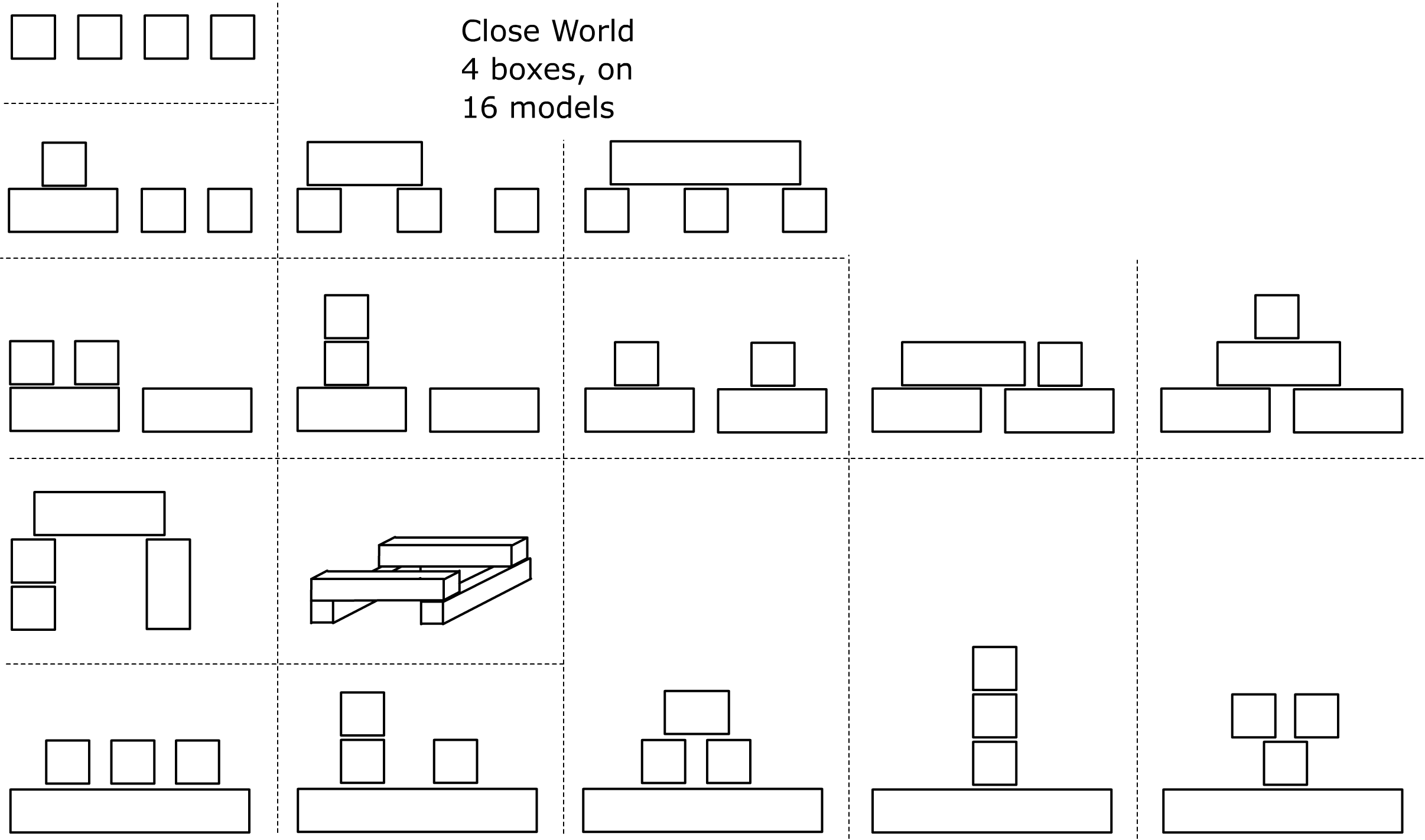
    Число неизоморфных моделей

    in,in#
    n  Close  Open 
    2 2 3
    3 4 10
    4 9 39
    5 20 160
    6 48 702
    in,in#,on,on#
    n  Close  Open 
    2 3 5
    3 11 38
    4 49 399
    5 245
    in,in#,on,on#,above
    n CloseOpen
    2 4 6
    3 24 67
    4 215 1292
    5 2715