Многомерные пространства

Введение

Мы живём в 3-мерном пространстве. Оно для нас на столько привычно, что свойства пространств большего числа измерений часто оказываются очень неожиданными. Тем не менее, именно с такими пространствами имеют дело в машинном обучении, где объекты обычно характеризуются n вещественными признаками. Рассмотрим некоторые математические аспекты многомерия.

Гиперкуб

Нормировкой всегда можно сделать так, чтобы значения каждого признака принадлежали интервалу от 0 до 1. Тогда все объекты представимы точками внутри n-мерного единичного гиперкуба в пространстве признаков.

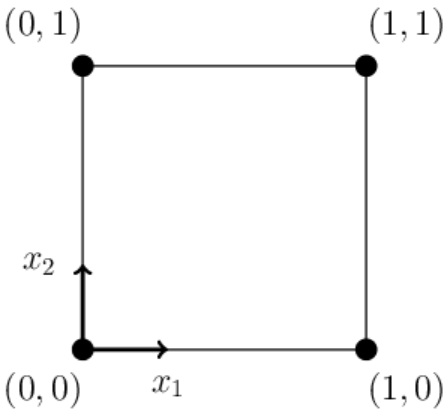
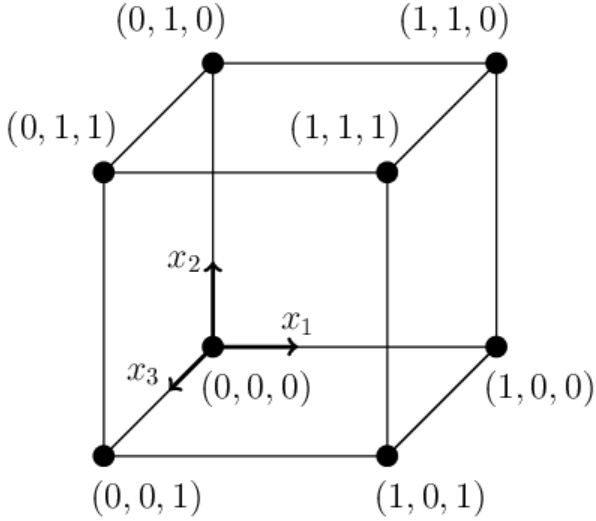
Единичный 2-мерный куб (квадрат на плоскости) имеет 4 вершины с координатами (0,0), (0,1), (1,0), (1,1). У 3-мерного куба их 8.

В пространстве n измерений: x = {x¹,...,xⁿ}. Пусть одна вершина куба находится в начале координат: {0,0,...,0} (n нулей). Остальные вершины нумеруются всеми возможными последовательностями n нулей и единиц: {0,0,...,0}, {1,0,...,0}, ..., {1,1,...,1}, поэтому:

Гиперкуб в n измерениях имеет 2ⁿ вершин

При больших n гирперкуб очень "колючий" объект. Например, при n=32 у него 4'294'967'296 вершин.

Из каждой $2^n$ вершин гиперкуба выходит $n$ рёбер (для вершины (0,0,...,0) это $n$ координатных осей). Поэтому всего у гиперкуба $n\,2^n/2=n\,2^{n-1}$ рёбер.

Диагональ, соединяющая точки {0,0,...,0} и {1,1,...,1}, имеет длину $\sqrt{n}$ (таких длинных диагоналей $n$ штук). "Сторона" гиперкуба - это $(n-1)$-мерный куб с $2^{n-1}$ вершинами (у 3-куба 6 сторон-квадратов). Таких сторон у гиперкуба $2\,n$ штук. Кроме этого, гиперкуб можно получить соединением рёбрами вершин двух $(n-1)$-мерных кубов (для "обычного" куба это два квадрата). При этом снова получается:

Гипотеза компактности

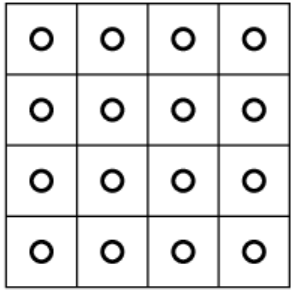Предположим, что мы хотим равномерно заполнить пространство признаков внутри гиперкуба точками (обучающими объектами). Для этого каждый признак (ось) разобьём на k равных частей. В результате получится kⁿ кубиков, в каждый из которых можно поместить точку. Понятно, что даже при k = 2 и n = 32 это сделать практически невозможно. Таким образом, многомерное пространство очень большое.

Необходимо стремится к такому отбору признаков объектов, при котором соответствующие их классам образы не были бы слишком сложными. Иногда это формулируют в виде гипотезы компактности:

Каждый класс должен занимать относительно компактную область в n-мерном пространстве, таким образом чтобы и различные классы оказывались отделимыми друг от друга сравнительно простыми поверхностями (в идеале гиперплоскостями).

Шар

Множество равноудалённых точек от данной (центра) называется сферой. Пространство внутри сферы называется шаром. Шар, вписанный в гиперкуб, это очень "маленький" объект. В $n$-мерном пространстве шар радиуса $R$ имеет следующие объём $V_n$ и площадь поверхности $S_n$: $$ V_n = C_n\cdot R^n,~~~~~~~~~~~~S_n = C_n\cdot n\,R^{n-1},~~~~~~~где~~~~~~C_n = \frac{ \pi^{n/2} }{\Gamma({n\over 2}+1)},~~~~~C_{2k} = \frac{\pi^k}{k!} $$ где $\Gamma(x)$ - гамма-функция: $\Gamma(1)=1,~~~$ $\Gamma(1/2)=\sqrt{\pi}$, $~~\Gamma(z+1) = z\,\Gamma(z)~~$ и $~~\Gamma(z+\alpha)=z^\alpha\,\Gamma(z)$ при $z \gg 1$.

В единичный гиперкуб можно вписать шар радиуса R=1/2. Его объём при n=10 равен V₁₀=0.0025, а при n=32 он исчезающе мал: V₃₂=10^-15. Хотя шар "прижимается" к граням гриперкуба, его окружает очень много (2ⁿ) углов.

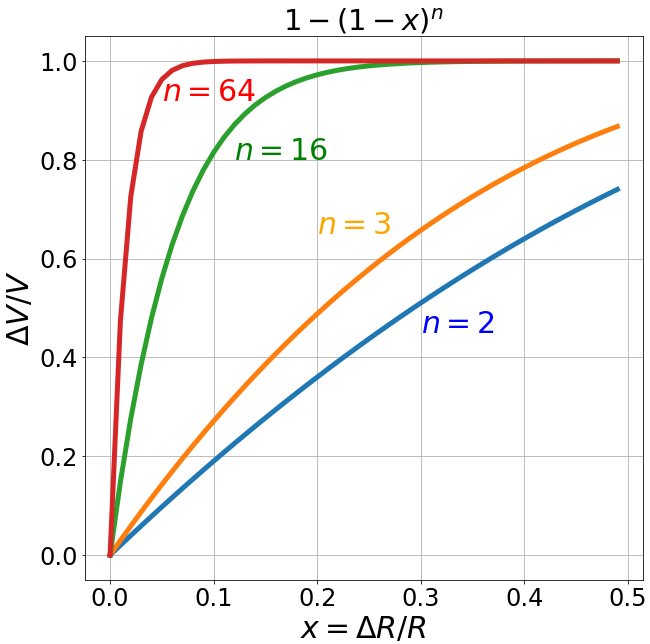Ещё одна особенность n-мерного шара состоит в том, что почти весь его объём сосредоточен возле поверхности. Действительно, рассмотрим два вложенных друг в друга шара с радиусами $R$ и $R-\Delta R$. Разность их объёмов равна объёму сферического слоя между ними. $$ \frac{\Delta V}{V} = \frac{R^n - (R-\Delta R)^n}{R^n} = 1 - \left(1-\frac{\Delta R}{R}\right)^n. $$ Отношение объёма слоя к объёму шара радиуса $R$ приведено на рисунке справа для различных размерностей пространства $n$.

Пусть шар равномерно (с постоянной плотностью) заполнен объектами. Случайно выбранный объект (при больших $n$) почти наверняка окажется возле поверхности шара.

Пусть объекты данного класса характеризуются некоторыми типичными (средними) значениями признаков с небольшим разбросом вокруг этих средних значений. Тогда образ этого класса является центром шара в n-мерном пространстве. Чем меньше разброс вокруг среднего, тем меньше радиус такого шара-образа. Если у разных признаков разброс имеет различную амплитуду, то шар становится эллипсоидом. Линейным преобразованием эллипсоид всегда можно превратить в шар. Однако, если в пространстве признаков существует несколько различных эллипсоидов, то линейным преобразованием превратить в шар можно только один из них.

Пространства эмбединга

При обработке текстов или изображений получают векторы признаков, для которых в качестве близости используется косинусное расстояние. В этом случае основным объектом удобнее рассматривать сферу единичного радиуса. Для чётных $n$ её объём равен: $$ V_2=3.14,~~~~~~~V_{16}=0.23,~~~~~~~V_{32}=4\cdot 10^{-6},~~~~~~~V_{64}=3\cdot 10^{-20},~~~~~~~~V_n=C_n=\frac{\pi^{n/2}}{(n/2)!}. $$

$$ D(\mathbf{x},\mathbf{y}) = (\mathbf{x}-\mathbf{y})^2 = \mathbf{x}^2 + \mathbf{y}^2 - 2\,\mathbf{x}\cdot \mathbf{y} $$ $$ D(\mathbf{x},\mathbf{y}) = 2\,\bigr(1-\cos(\mathbf{x},\mathbf{y})\bigr). $$

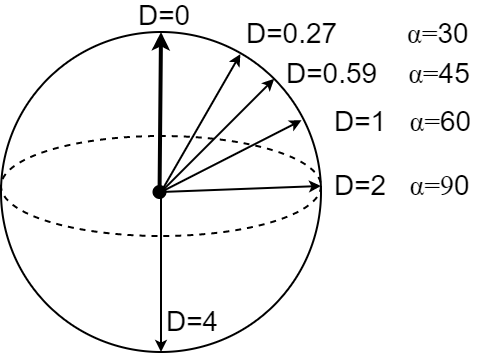
Если на "поверхности" $(n-1)$-мерной гиперсферы, провести $(n-2)$-мерную сферу радиуса $r$, то отношение площади гиперсферы и объёма сферы будет порядка: $$ \frac{S_n(R)}{V_{n-1}(r)} \approx \sqrt{2\pi n}\, \left(\frac{R}{r}\right)^{n-1} $$ Так, на единичной $n$-гиперсфере $R=1$ проведём ($n-1$)-сферу радиуса $r=1/2$ (пол радиана или 28°). Тогда в 100-мерном пространстве, таких непересекающихся сфер может быть порядка $2^{100}$. Следовательно в них могут разместиться кластеры объектов различных классов. Многомерное пространство сущесвенно более "вместительно".

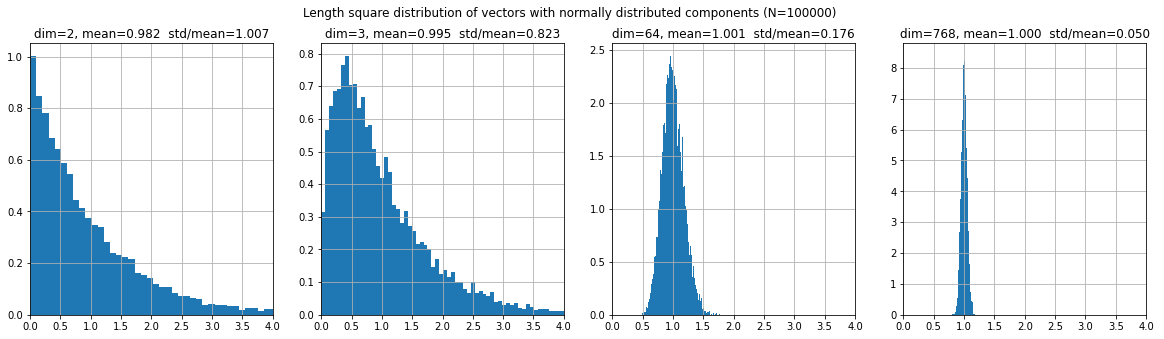
Если компоненты вектора являются случайными гауссовыми числами $\varepsilon$ с нулевым средним и единичной дисперсией, то среднее значение квадрата его длины равно размерности пространства: $$ \langle \mathbf{x}^2\rangle = \langle \varepsilon^2_1+...+\varepsilon^2_1\rangle = n. $$ При этом вероятность распределения квадрата длины $D=\mathbf{x}^2$ при больших $n$ в окрестности $n-2$ имеет узкий пик (все точки "собираются" в окрестности сферы): $$ \frac{e^{-(\varepsilon^2_1+...+\varepsilon^2_n)/2}} {(2\pi)^{n/2}}\, d\varepsilon_1...d\varepsilon_n = \frac{\Omega_n}{(2\pi)^{n/2}}\, e^{-r^2/2}\, r^{n-1}\,dr = \frac{\Omega_n}{2(2\pi)^{n/2}}\, e^{-D/2}\, D^{n/2-1}\,dD $$ Смоделируем это при помощи библиотеки numpy:

X = np.random.normal(0.0, 1, (10000, dim))/dim**0.5        
R2 = (X*X).sum(axis=1)

m-мерные плоскости

Пусть $\mathbf{x}=\{x^1,...,x^n\}$ - точка в $n$-мерном пространстве (верхний индекс - номер координаты). Поверхность размерности $m$ можно описать параметрическим образом $$ \mathbf{x} = \mathbf{f}(t_1,...,t_m), $$ где $t_k$ - набор скалярных параметров (их количество равно размерности поверхности). Например, единичная сфера в 3-мерном пространстве описывается двумя (2-мерный объект) углами $\{t_1,t_2\}=\{\theta,\phi\}$: $$ x = \sin \theta \cos\phi, ~~~~~y = \sin \theta \sin\phi,~~~~~z = \cos \theta. $$ Самой простой $m$-мерной поверхностью является плоскость. Пусть $\mathbf{e}_k=\{\mathbf{e}_1,...,\mathbf{e}_m\}$ - набор $m$ единичных, попарно ортогональных векторов ($\mathbf{e}_k\mathbf{e}_p=\delta_{pk}$, где $\delta_{pk}$ - символ Кронекера). Тогда уравнение плоскости имеет вид: \begin{equation}\label{plane_eq} \mathbf{x}= \mathbf{x}_0 + \sum^m_{k=1} t_k\mathbf{e}_k. \end{equation} Параметры $\{t_1,...,t_m\}$ выступают декартовыми координатами в $m$-мерном пространстве с базисом $\{\mathbf{e}_1,...,\mathbf{e}_m\}$. Вектор $\mathbf{x}_0$ задаёт положение начала координат (точка $n$-пространства, в которой на плоскости все координаты $t_k$ равны нулю). Уравнение (\ref{plane_eq}) является первым приближением разложения в ряд Тейлора произвольной поверхности $\mathbf{x} = \mathbf{f}(t_1,...,t_m)$ в окрестности точки $t_1=...=t_m=0$. Если $m=1$, то (\ref{plane_eq}) будет уравнением прямой (одномерный объект). При $m=2$ мы имеем двумерную плоскость и т.д.

Расстояние до $m$-плоскости

Получим выражение для кратчайшего евклидового расстояния $(\mathbf{x}-\mathbf{X})^2$ от произвольной точки $\mathbf{X}$ до $m$-плоскости (\ref{plane_eq}). Для этого необходимо найти параметры $t_k$ для которых это расстояние минимально: $$ d^2 = \bigr(\mathbf{x}_0-\mathbf{X} + \sum^m_{k=1} t_k\mathbf{e}_k\bigr)^2 = \min. $$ Возьмём производную по $t_p$, приравняем её нулю и учтём ортонормированность векторов $\mathbf{e}_k$: $$ \bigr(\mathbf{x}_0-\mathbf{X} + \sum^m_{k=1} t_k\mathbf{e}_k\bigr)\,\mathbf{e}_p = (\mathbf{x}_0-\mathbf{X})\,\mathbf{e}_p + t_p = 0 ~~~~~~~~\Rightarrow~~~~~~~t_p = -(\mathbf{x}_0-\mathbf{X})\,\mathbf{e}_p. $$ Подставим эти $t_p$ в квадрат расстояния $d^2$: $$ d^2 = \bigr(\mathbf{x}_0-\mathbf{X} - \sum^m_{k=1} \bigr[(\mathbf{x}_0-\mathbf{X})\,\mathbf{e}_k \bigr]\,\mathbf{e}_k\bigr)^2. $$ Возводя в квадрат (снова с учётом ортогональности), это выражение можно переписать в следующем виде: \begin{equation}\label{d2_to_plane} d^2 = \bigr(\mathbf{x}_0-\mathbf{X}\bigr)^2 - \sum^m_{k=1} \bigr[(\mathbf{x}_0-\mathbf{X})\,\mathbf{e}_k \bigr]^2. \end{equation} Проекция точки $\mathbf{X}$ на плоскость получается подстановкой найденных параметров $t_k$ в уравнение плоскости (\ref{plane_eq}): \begin{equation}\label{projec_coord} \mathbf{X} ~\mapsto~\mathbf{x}=\mathbf{x}_0 + \sum^m_{k=1} \bigr[(\mathbf{X}-\mathbf{x}_0)\,\mathbf{e}_k\bigr]\mathbf{e}_k. \end{equation}

Гиперплоскость

Гиперплоскостью в $n$-мерном пространстве называют $m=(n-1)$-мерную плоскость. (в 2-мерии это линия, а в 3-мерии "обычная" плоскость). Гиперплоскость всегда можно провести через $n$ точек. Соответственно, она задаётся при помощи $n$ чисел (например, единичным ($\boldsymbol{\omega}^2=1$) вектором нормали (перпендикуляра) к плоскости $\boldsymbol{\omega} = \{\omega^1,....,\omega^n\}$ и параметром сдвига $\omega_0$.

Пусть гиперплоскость проходит через точку $\mathbf{x}_0$ и имеет вектор нормали $\boldsymbol{\omega}$. Тогда расстояние d от гиперплоскости до некоторой точки $\mathbf{X}=\{X^1,...,X^n\}$ вычисляется по формуле

При этом $d > 0$, если точка $\mathbf{X}$ лежит с той стороны плоскости, куда указывает вектор $\boldsymbol{\omega}$ и $d < 0$, если с противоположной. Когда $d=0$ - точка $\mathbf{X}$ лежит в плоскости. Изменение параметра $\omega_0$ сдвигает плоскость параллельным образом в пространстве. Если $\omega_0$ уменьшается, то плоскость смещается в направлении вектора $\boldsymbol{\omega}$ (расстояние меньше), а если $\omega_0$ увеличивается - плоскость смещается против вектора $\boldsymbol{\omega}$. Это непосредственно следует из приведенной выше формулы.

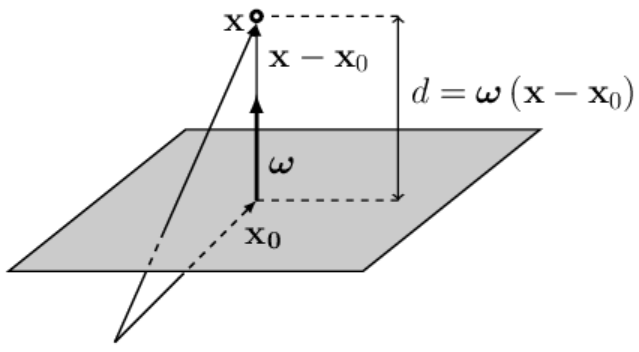◄ Запишем вектор $\mathbf{X}-\mathbf{x}_0$, начинающийся в точке $\mathbf{x}_0$ (лежащей в плоскости) и направленный в точку $\mathbf{X}$ (векторы складываются по правилу треугольника). Точка $\mathbf{x}_0$ выбрана в основании вектора $\boldsymbol{\omega}$, поэтому $\boldsymbol{\omega}$ и $\mathbf{X}-\mathbf{x}_0$ коллинеарны (лежат на одной прямой). Если вектор $\boldsymbol{\omega}$ единичный ($\boldsymbol{\omega}^2=1$), то скалярное произведение векторов $d=\boldsymbol{\omega}\,(\mathbf{X}-\mathbf{x}_0)$ равно расстоянию $d$ точки $\mathbf{X}$ до плоскости.

Если длина $\omega=|\boldsymbol{\omega}|$ вектора $\boldsymbol{\omega}$ отлична от единицы, то $d$ в $\omega$ раз больше ($\omega > 1$) или меньше ($\omega < 1$) евклидового расстояния в $n$-мерном пространстве. Когда векторы $\boldsymbol{\omega}$ и $\mathbf{X}-\mathbf{x}_0$ направлены в противоположные стороны: $d < 0$. ►

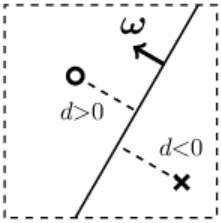Если пространство имеет n измерений, то гиперплоскость это (n-1)-мерный объект.
Она делит всё пространство на две части. Для наглядности рассмотрим 2-мерное пространство. Гиперплоскостью в нём будет прямая линия (одномерный объект). Справа на рисунке кружок изображает одну точку пространства, а крестик - другую. Они расположены по разные стороны от линии (гиперплоскости). Если длина вектора ω много больше единицы, то и расстояния d от точек к плоскости по модулю будут существенно большими единицы.

Уравнение гиперплоскости, аналогично $m$-плоскости, можно записать в параметрическом виде при помощи $n-1$ векторов базиса $\{\mathbf{e}_1,...,\mathbf{e}_{n-1}\}$. Все эти векторы ортогональны вектору нормали: $\boldsymbol{\omega}\mathbf{e}_k=0$.

Симплекс

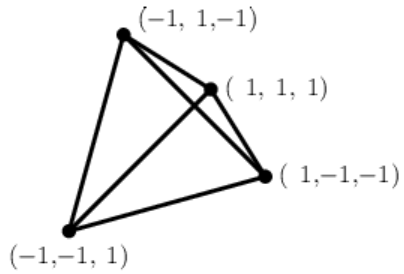Симплексом называют n мерное обобщение треугольника 2-мерного пространства. В 3-мерии это тетраэдр (рисунок справа). Через n точек в n-мерном пространстве можно провести гиперплоскость. Соответственно n+1 точек в общем случае не лежат на одной гиперплоскости и образуют симплекс с n+1 вершинами. Если все рёбра (расстояния между парами вершин) одинаковы - симплекс называют правильным. Напротив каждой из n+1 вершин лежит гиперплоскость (в которую эта вершина не попала).

Каждая из $n+1$ вершин симплеса соединена со всем остальными вершинами рёбрами. Соответственно, число рёбер равно $n\,(n+1)/2$.

Объём правильного симплекса с единичными рёбрами равен: $$ V_n = \frac{\sqrt{n+1}}{n!\,2^{n/2}}. $$ Как и шар, это очень "маленький" объект.

Пусть внутри сферы находятся объекты одного класса, а вне неё - объекты другого класса. Для их разделения потребуется нейронная сеть с одним скрытым слоем, имеющая по меньшей мере n+1 нейронов в скрытом слоёв. Они образуют n+1 гиперплоскостей симплекса (возможно со сглаженными углами, если длины векторов нормали невелики).

Немного математики