ML: Введение в машинное обучение
Введение
 Методы машинного обучения являются подмножеством алгоритмов искусственного интеллекта.
В свою очередь, нейронные сети и глубокое обучение - это частный случай машинного обучения.
Данный документ является вводным и описывает основные понятия машинного обучения и типы
решаемых с его помощью задач.
Методы машинного обучения являются подмножеством алгоритмов искусственного интеллекта.
В свою очередь, нейронные сети и глубокое обучение - это частный случай машинного обучения.
Данный документ является вводным и описывает основные понятия машинного обучения и типы
решаемых с его помощью задач.
Объекты и их признаки
 Пусть есть множество однотипных объектов:
бутылки с вином, посетители в больнице или позиции на шахматной доске (это три различных множества).
Каждый объект множества характеризуется набором (вектором) признаков:
$\mathbf{x}= \{x_0,x_1,...,x_{n-1}\}$.
Пусть есть множество однотипных объектов:
бутылки с вином, посетители в больнице или позиции на шахматной доске (это три различных множества).
Каждый объект множества характеризуется набором (вектором) признаков:
$\mathbf{x}= \{x_0,x_1,...,x_{n-1}\}$.
Признаки могут быть:
- числовые (вес, рост, яркость пикселя)
- бинарные (женщина/мужчина, живой/мёртвый)
- упорядоченные нечисловые (маленький/большой/огромный)
- качественные нечисловые (красный/синий/зелёный)
Задачи машинного обучения
Объекты данного множества иногда можно разбить на классы (человек: {здоровый, больной}, вино: {итальянское, французское, грузинское}). Кроме этого, с каждым объектом можно связать некоторое число y (степень преимущества белых в шахматной позиции; качество вина по усреднённому мнению экспертов и т.д.). Соответственно, часто решаются две задачи: классификация - к какому из классов принадлежит объект и регрессия - какое число или набор чисел соответствует объекту. Примеры:
- 1) 3 признака: x={температура, гемоглобин, холестерин}; 2 класса: {0: здоровый, 1: больной};
- 2) w*h признаков: x={яркости пикселей картинки размером w на h}; 10 классов: {0-9: цифра на картинке}.
- 3) 8*8*13 признаков: x={коды шахматных фигур}; регрессия: преимущество белых на чёрными =[-1...1].
Для успешного решения задач классификации или регрессии, признаки, характеризующие объект, должны быть значимыми, а вектор признаков - полным (достаточным для классификации объектов или определении регрессионной величины y).
Кроме классификации и регрессии возможны и другие задачи. Так, при ранжировании требуется упорядочить по некоторому критерию множество объектов (например, документов, полученных по поисковому запросу). В последнее время важную роль играют генеративные задачи: по упорядоченной последовательности объектов из данного множества сгенерить другую последовательность из объектов этого же или другого множества. Примерами являются: системы машинного перевода, текстовое аннотирование изображений или генерация фейковых видео.
Обучение с учителем
 Систему, решающую задачу классификации или регрессии представим в виде чёрного ящика.
У него есть n входов, на которые подаются значения признаков
$\mathbf{x} = \{x_0,...,x_{n-1}\}$
и $m$ выходов $\mathbf{y} = \{y_0,...,y_{m-1}\}$.
В задаче классификации $m$ равно числу классов, а в задаче регрессии -
числу зависимых величин, связанных с каждым объектом.
Модель можно считать многомерной функцией или алгоритмом $\mathbf{y}=f(\mathbf{x},\,\boldsymbol{\omega})$,
которая по данному $\mathbf{x}$ выдаёт значение $\mathbf{y}$.
Вектор $\boldsymbol{\omega}$ - это параметры модели.
Систему, решающую задачу классификации или регрессии представим в виде чёрного ящика.
У него есть n входов, на которые подаются значения признаков
$\mathbf{x} = \{x_0,...,x_{n-1}\}$
и $m$ выходов $\mathbf{y} = \{y_0,...,y_{m-1}\}$.
В задаче классификации $m$ равно числу классов, а в задаче регрессии -
числу зависимых величин, связанных с каждым объектом.
Модель можно считать многомерной функцией или алгоритмом $\mathbf{y}=f(\mathbf{x},\,\boldsymbol{\omega})$,
которая по данному $\mathbf{x}$ выдаёт значение $\mathbf{y}$.
Вектор $\boldsymbol{\omega}$ - это параметры модели.
Машинное обучение подразумевает наличие обучающего множества объектов $\mathcal{T}$. Его предоставляет "учитель" (обычно человек). На этом множестве система обучается (настраивает модель = оптимизирует параметры $\boldsymbol{\omega}$). Правильно обученная система должна выдавать корректные результаты на выходе не только на обучающем, но и на тестовом множестве объектов $\mathcal{V}$, которые не использовались при обучении: $\mathcal{T}\cap \mathcal{V}=\varnothing$.
Для машинного обучения типичны две проблемы: недообучение (under-fitting)
и переобучение (over-fitting).
Недообучение возникает когда модель слишком простая и не способна выразить природу обучающих данных.
Например, в такой модели может быть недостаточное количество "настроечных" параметров.
Переобучение - это противоположная ситуация: в модели слишком много параметров и она стремятся
"запомнить" все обучающие объекты, включая неизбежный шум или ошибки.
В этом случае модель не способна к обобщению или экстраполяции и очень плохо работает
на тестовых данных.
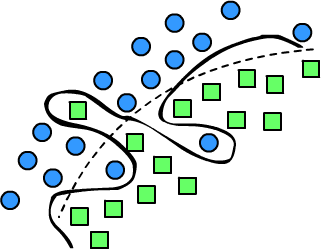 Справа изображена задача классификации двух классов (круги и квадраты)
в двумерном пространстве признаков. Пунктирная линия является гладкой разделяющей поверхностью,
которая отделяет объекты одного класса от объектов второго. Три объекта эта поверхность относит к неправильным
классам. Эту ситуацию "исправляет" волнистая линия. Однако, если эти три объекта являются случайными
выбросами, волнистая линия - пример типичного переобучения.
Справа изображена задача классификации двух классов (круги и квадраты)
в двумерном пространстве признаков. Пунктирная линия является гладкой разделяющей поверхностью,
которая отделяет объекты одного класса от объектов второго. Три объекта эта поверхность относит к неправильным
классам. Эту ситуацию "исправляет" волнистая линия. Однако, если эти три объекта являются случайными
выбросами, волнистая линия - пример типичного переобучения.
Среднеквадратичная ошибка
Рассмотрим $N$ объектов характеризующихся $n$-мерными векторами признаков. Их можно представить в виде матрицы $x_{i\alpha}$, где первый индекс $i=0...N-1$ - это номер объекта, а второй индекс $\alpha=0...n-1$ - номер его признака. Пусть для каждого ($i$-того) примера $\hat{\mathbf{x}}_i=\{\hat{x}_{i0},...,\hat{x}_{i,n-1}\}$ из обучающего множества известны "истинные" значения выходов модели (например, в задаче регрессии). Будем их помечать шляпкой: $\hat{\mathbf{y}}_i=\{\hat{y}_{i0},...,\hat{y}_{i,m-1}\}$. Чем ближе $\mathbf{y}=f(\hat{\mathbf{x}},\,\boldsymbol{\omega})$ к истинным значениям $\hat{\mathbf{y}}$, тем лучше работает модель.
Среднеквадратичной ошибкой (MSE, mean squared error) называется среднее квадратов отклонений предсказаний $y_{i\alpha}$ модели от истинных значений $\hat{y}_{i\alpha}$ по каждому примеру ($i$) и каждому выходу ($\alpha$):
$$ L = \langle(\mathbf{y}-\hat{\mathbf{y}})^2 \rangle ~=~ \frac{1}{N\cdot m}\sum^{N-1}_{i=0}~\sum^{m-1}_{\alpha=0} ~~(y_{i\alpha}-\hat{y}_{i\alpha})^2. $$ Так как модель $\mathbf{y} = f(\hat{\mathbf{x}}, \boldsymbol{\omega})$ и обучающее множество $\{\hat{\mathbf{x}},\hat{\mathbf{y}}\}$ заданы, ошибка зависит только от параметров модели $L=L(\boldsymbol{\omega})$. В процессе машинного обучения эти параметры подбираются так, чтобы ошибка достигла своего минимального значения: $\bar{\boldsymbol{\omega}} = \text{argmin} \,L(\boldsymbol{\omega})$.
Существенным достоинством MSE является то, что она дифференцируема по выходам модели $\mathbf{y}$ а, следовательно, дифференцируема по её параметрам (если дифференцируема функция $f$): $$ \frac{\partial L}{\partial \boldsymbol{\omega}} ~=~ \sum_{i,\alpha} \frac{\partial L}{\partial y_{i\alpha}} \frac{\partial y_{i\alpha}}{\partial \boldsymbol{\omega}} ~=~ \frac{2}{N\cdot m}\sum_{i,\alpha} ~~(y_{i\alpha}-\hat{y}_{i\alpha})\,\frac{\partial f_{i\alpha}(\hat{\mathbf{x}}_i,\,\boldsymbol{\omega})}{\partial \boldsymbol{\omega}}. $$ Это свойство среднеквадратичной ошибки позволяет использовать мощный оптимизационный метод градиентного спуска для подбора параметров модели.
Бинарная классификация
 В задаче бинарной классификации объект с признаками $\mathbf{x}$
необходимо отнести к одному из двух классов: $c\in \{0,1\}$.
Будем считать, что у модели есть единственный выход $y$
со значениями, лежащими в диапазоне [0...1].
Тогда правило классификации записывается следующим образом: $c = [y > 0.5]$.
Квадратные скобки вокруг логического условия [condition] означают число 0,
если условие ложно и 1, если истинно.
Таким образом, если выход модели меньше или равен 0.5, мы считаем, что это класс $c=0$,
в противном случае - это класс $c=1$.
В задаче бинарной классификации объект с признаками $\mathbf{x}$
необходимо отнести к одному из двух классов: $c\in \{0,1\}$.
Будем считать, что у модели есть единственный выход $y$
со значениями, лежащими в диапазоне [0...1].
Тогда правило классификации записывается следующим образом: $c = [y > 0.5]$.
Квадратные скобки вокруг логического условия [condition] означают число 0,
если условие ложно и 1, если истинно.
Таким образом, если выход модели меньше или равен 0.5, мы считаем, что это класс $c=0$,
в противном случае - это класс $c=1$.
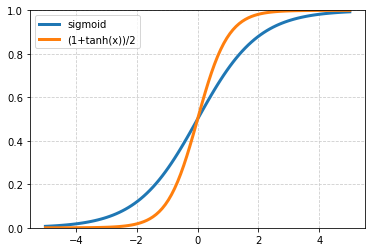 ☝ Масштабирование выхода модели к интервалу $[0...1]$ всегда можно осуществить при помощи сигмоидной функции:
$$
y = \sigma(x) = \frac{1}{1+e^{-x}},~~~~~~~~~~~\frac{dy}{dx} = y\cdot(1-y).
$$
При больших $x$ сигмоида быстро стремится к единице, при больших по модулю отрицательных - к нулю и $\sigma(0)=1/2$.
Альтернативно можно использовать гиперболический тангенс: $y=(1+\tanh(x))/2$ с такими же свойствами.
☝ Масштабирование выхода модели к интервалу $[0...1]$ всегда можно осуществить при помощи сигмоидной функции:
$$
y = \sigma(x) = \frac{1}{1+e^{-x}},~~~~~~~~~~~\frac{dy}{dx} = y\cdot(1-y).
$$
При больших $x$ сигмоида быстро стремится к единице, при больших по модулю отрицательных - к нулю и $\sigma(0)=1/2$.
Альтернативно можно использовать гиперболический тангенс: $y=(1+\tanh(x))/2$ с такими же свойствами.
В качестве ошибки модели (которую минимизируют) можно взять среднеквадратичную ошибку MSE, считая, что в обучающем множестве для первого класса $\hat{y}_i = 0$, а для второго: $\hat{y}_i = 1$: $$ L = \frac{1}{N}\sum_{i} (y_i - \hat{y}_i)^2 ~=~ \frac{1}{N}\sum_{i} \left\{ \begin{array}{cl} y^2_i, & \hat{y}_i =0\\ (1-y_i)^2, & \hat{y}_i = 1 \end{array} \right\}. $$ Чем ближе выход модели к нулю или единице, тем она более "уверенна", а при $y\sim 0.5$ модель "не знает" к какому классу необходимо отнести объект.
Так как выход $y$ модели $f(\mathbf{x},\,\boldsymbol{\omega})$ лежит в интервале [0...1], его можно интерпретировать как условную "вероятность" $y=p(c=1|\mathbf{x})$ принадлежности объекта $\mathbf{x}$ к классу $c=1$. Соответственно, $1-y = p(c=0|\mathbf{x})$ - это вероятность принадлежности к классу $c=0$. Если $\hat{y}=1$, то необходимо максимизировать вероятность $y$, а если $\hat{y}=0$, то максимизировать вероятность $1-y$. Максимум вероятности соответствует минимуму её логарифма с отрицательным знаком. В результате мы получаем следующую альтернативу MSE: $$ L = -\frac{1}{N}\sum_{i} \Bigr[ \hat{y}_i \,\log y_i + (1-\hat{y}_i)\,\log(1-y_i) \Bigr] ~=~ -\frac{1}{N}\sum_{i} \left\{ \begin{array}{cl} \log (1-y_i), & \hat{y}_i =0\\ \log y_i, & \hat{y}_i = 1 \end{array} \right\}, $$ которую называют бинарной кросс-энтропией (BCE, binary cross entropy). Приведём графики $L(y)$ для MSE и BSE при $\hat{y}=0$ и $\hat{y}=1$:
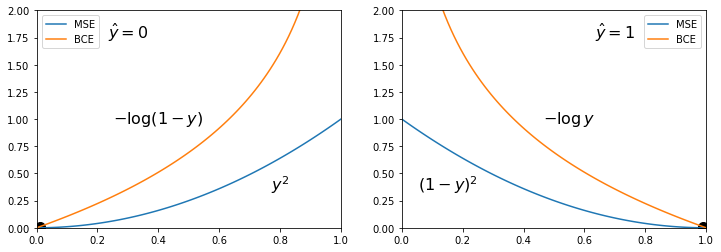
BСE круче подходит к целевому значению $y=\hat{y}$, чем MSE и линейна в окрестности целевого значения. Именно это обусловливает большую популярность использования BCE в задаче бинарной классификации.
Аккуратность модели
Введенные выше ошибки удобны при поиске оптимальных параметров (например, градиентным методом). Тем не менее, для практических целей, необходимы дополнительные оценки качества модели, которые проще интерпретировать. Особенно это относится к задачам классификации. Для бинарной классификации наиболее простой и естественной является мера аккуратности модели, равная доле правильно предсказанных ею классов: $$ A =\frac{\text{correct}}{\text{total}} = \frac{1}{N}\sum_i \bigr[ [y_i > 0.5 ] = \hat{y}_i \bigr] $$ Если $A=1$, это означает, что модель правильно относит все объекты к их классам. При $A=0.5$ - она работает не лучше генератора случайных чисел.
Приведём пример вычисления ошибок и аккуртности модели при помощи библиотеки NumPy:
import numpy as np # подключение библиотеки numpy
y = np.array([0.1, 0.8, 0.6, 0.2]) # выход для 4-х примеров
c = np.array([0, 1, 0, 0]) # их истинные классы
mse = np.mean( (y-c)**2 ) # среднеквадратичная ошибка
bce = np.mean( -c*np.log(y)-(1-c)*np.log(1-y) ) # бинарная кросс-энтропия
acc = np.mean( (y > 0.5) == c ) # аккуратность модели
print(f'mse:{mse:0.2f}, bce:{bce:0.2f}, acc:{acc:0.2f}') # mse:0.11, bce:0.37, acc:0.75
В массиве "y" находятся результаты выхода модели для четырёх примеров,
а в массиве "с", соответствующие им "истинные" классы (бинарная классификация).
В худшем случае, когда модель сомневается всегда (на выходе для любого $\mathbf{x}$ получатся 0.5), ошибки равны: mse=0.25 и bce=0.69, т.е. bce больше mse, но обе равны нулю в точке минимума (см. рисунок выше).
Позитивный и негативный класс
Критерий аккуратности имеет смысл, когда число объектов каждого класса примерно одинаково. Однако часто объектов одного типа больше чем второго. Модель, которая всегда предсказывает более частотный класс будет иметь неплохую аккуратность (равную частоте этого класса), но по факту она ничему не научена.
В медицинской диагностике используются термины позитивный (positive)
и негативный (negative).
Результаты тестов (анализов) негативные, если
паталогия (болезнь) не выявлена, а если выявлена - позитивные.
Соответственно, для случайно выбранного человека вероятность негативных результатов существенно
выше, чем позитивных. Поэтому в бинарной классификации при заметном перекосе
в частотности классов, более вероятный класс принято называть негативным, а менее вероятный - позитивным.
Нарисуем множество объектов. Слева от вертикальной пунктирной линии находятся объекты негативного класса, а справа - позитивного. Жирная волнистая линия разделяет негативные и позитивные классы с "точки зрения" модели. При этом она совершает ошибки двух видов:
- ложное срабатывание (FP, false positive) - объекты отрицательного класса
принимаются за позитивные
(здоровых считают больными), ниже жёлтый цвет; - пропуск (FN, false negative) - объекты позитивного класса
принимаются за негативные объекты
(не выявляют больного) - ниже зелёный цвет.
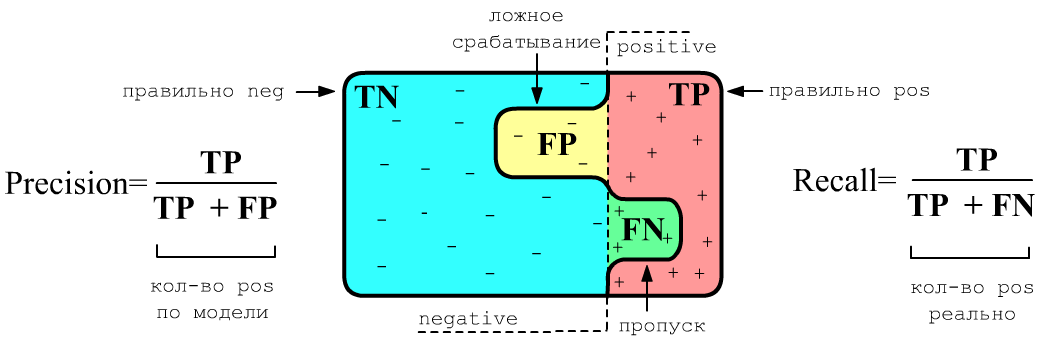
Используя эти определения, введём две меры качества работы модели, формулы для которых приведены на рисунке. Precision (точность) равна доле правильных предсказаний позитивного класса к общему количеству выданных моделью позитивных классов. Recall (полнота) - аналогичная доля, но отнесенная к истинному числу позитивных примеров в данных. Эти две меры не так чувствительны к перекосу в частотности классов, чем аккуратность (TN+TP)/N, где N = TN+TP + FN+FP - общее число примеров.
Ниже в обучающем множестве из 100 объектов находится 92 примера первого класса (негативного) и 8 второго (позитивного). Модель очень плохо распознаёт позитивный класс (1 раз верно и 7 неверно), хотя аккуратность достаточно высокая. Проблему отражают точность и полнота:
$$ \begin{array}{|c|c|} \mathbf{N} & \mathbf{P}\\ \hline \hline \mathbf{TN} & \mathbf{FN} \\ \hline \mathbf{FP} & \mathbf{TP} \\ \hline \end{array} ~=~ \begin{array}{|r|r|} \mathbf{N} & \mathbf{P}\\ \hline 90 & ~7 \\ \hline 2 & 1 \\ \hline \end{array}~~~~~~~~~~~~ \text{Accuracy} = 0.910,~~~~~~~\text{Precision} = 0.333,~~~~~~~~~\text{Recal} = 0.125 $$Иногда для измерения аккуратности требуется одно число. В этом случае можно произвести геометрическое усреднение, которое называется F1-мерой:
$$ F_1 = \frac{2}{\displaystyle\frac{1}{\text{Precision}} + \frac{1}{\text{Recall}}} = \frac{\mathbf{TP}}{\mathbf{TP}+ (\mathbf{FP}+\mathbf{FN})/2} $$У различных ошибок, в зависимости от задачи, может быть разная цена. Например пропуск больного FN более опасен, чем неверный диагноз FP для здорового человека. Поэтому, например, Precision можно вычислить для позитивного и негативного классов и сложить с весами, пропорциональными стоимости ошибки.
Множественная классификация
Рассмотрим теперь задачу классификации с числом классов $C > 2$. В этом случае количество выходов модели должно равняться числу классов. Пусть значения каждого $c$-того выхода по-прежнему находятся в диапазоне [0...1] и интерпретируются как степень уверенности того, что объект принадлежит к $c$-тому классу.
Классы могут пересекаться или не пересекаться. В первом случае объект с признаками $\mathbf{x}$ может принадлежать не одному, а нескольким классам. Например для $C=3$ может быть верным выход модели $\hat{\mathbf{y}}=\{0,1,1\}$ (второй и третий класс, но не первый). Для не пересекающихся классов, любой объект всегда принадлежит только одному классу. В этом случае также существует две возможности: строгая и нечёткая классификации. При строгой классификации $\hat{\mathbf{y}}$ содержит одну единицу на $c$-том выходе, а на остальных выходах - нули (объект точно относится к классу $c$). При нечёткой классификации объект относится к единственному классу, но с определённой вероятностью. В этом случае все выходы $\hat{\mathbf{y}}$ могут быть отличными от нуля, но их сумма должна равняться единице.
Классификацию с большим числом признаков можно свести бинарной классификации. Для этого необходимо взять $C$ моделей, каждая из которых отличает "свой" класс от всех остальных классов (которые она не различает). При тестировании выбирают наиболее "уверенную" модель и считают, что объект принадлежит её классу.
Для не пересекающихся классов всегда можно отнормировать значения выходов модели таким образом чтобы их сумма (для данного входа) равнялась единице. Тогда на выходе получается распределение вероятностей принадлежности к тому или иному классу.☝ Если выходы модели интерпретируются как вероятности, то их значения должны лежать в интервале $[0...1]$, а сумма равняться единице. Этого можно добиться, поставив на выходе модели функцию softmax: $$ p_i = \text{sm}(\mathbf{y}) = \frac{e^{y_i}}{\sum_k e^{y_k}},~~~~~~~~~~~~~~~~~~~~~p_i > 0,~~~~~~\sum_k p_k = 1. $$ Отметим, что софтмакс $\mathbf{p}=\text{sm}(\mathbf{y})$ неоднозначная функция. Если к каждой компоненте вектора $\mathbf{y}$ добавить одно и тоже число, то результат функции не изменится: $\text{sm}(\mathbf{y}+a) = \text{sm}(\mathbf{y})$.
y = [1, 3, 5, -3] # значения на выходах модели p = np.exp(y) p /= p.sum() # [0.016 0.117 0.867 0. ]
Ошибка по кросс-энтропии
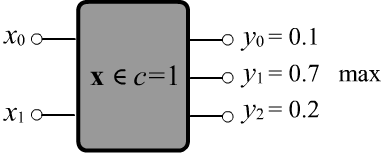 Пусть классы не пересекаются и известно, что $i$-й пример обучающего множества относится к классу $c=c(i)$.
Выходы модели считаем вероятностями классов (их сумма равна единице).
При строгой классификации работа модели тем лучше, чем больше в среднем эти вероятности.
Поэтому, в качестве функции потерь (которую необходимо минимизировать)
можно взять среднее от логарифма вероятности на выходе $y_{i,с(i)}$ с обратным знаком:
$$
L = -\frac{1}{N}\sum^{N-1}_{i=0} ~ \ln y_{i,c(i)}.
$$
Эту ошибку называют кросс-энтропией (CE, сross-entropy).
Эту же формулу можно применять в бинарной классификации, сделав у модели два выхода.
Пусть классы не пересекаются и известно, что $i$-й пример обучающего множества относится к классу $c=c(i)$.
Выходы модели считаем вероятностями классов (их сумма равна единице).
При строгой классификации работа модели тем лучше, чем больше в среднем эти вероятности.
Поэтому, в качестве функции потерь (которую необходимо минимизировать)
можно взять среднее от логарифма вероятности на выходе $y_{i,с(i)}$ с обратным знаком:
$$
L = -\frac{1}{N}\sum^{N-1}_{i=0} ~ \ln y_{i,c(i)}.
$$
Эту ошибку называют кросс-энтропией (CE, сross-entropy).
Эту же формулу можно применять в бинарной классификации, сделав у модели два выхода.
Для $C$ классов, если модель случайно и равновероятно ($y_\alpha\sim 1/C$) выдаёт произвольный класс, то $L=\log C$ или $\exp(L)$ равно числу классов. Если же модель работает безошибочно, то $L=0$.
В случае нечёткой классификации с не пересекающимися классами, можно задавать распределение вероятности $\hat{y}_{i\alpha}$ того, что $i$-й пример принадлежит к классу $\alpha$. Тогда функция потерь будет равна: $$ L = -\frac{1}{N}\sum^{N-1}_{i=0}~\sum^{C-1}_{\alpha=0} ~~\hat{y}_{i\alpha}\, \ln y_{i\alpha}. $$ Такая кросс-энтропия двух распределений вероятностей $\hat{\mathbf{y}}_{\alpha}$ и $\mathbf{y}_{\alpha}$ достигает минимума, при совпадении этих вероятностей. В частном случае, когда для $i$-го примера $\hat{y}_{i\alpha}=\{0,...,0,1,0,...0\}$, где $1$ стоит на позиции $c(i)$, если пример относится к классу под номером $c(i)$, мы возвращаемся к предыдущему случаю.
Для задач с пересекающимися классами, обычно, используют MSE, т.к. в этом случае сумма выходов не равна единице. Поэтому максимизация только вероятностей "правильных классов" не гарантирует минимизации выходов для "неправильных классов" (в MSE, в отличии от CE, присутствуют все классы).
Критерии аккуратности в общем случае
Когда классов более двух, можно по-прежнему использовать аккуратность, равную отношению правильных классификаций к общему числу примеров. Но это будет достаточно грубой метрикой. Более детальной мерой качества является матрица ошибок (confusion matrix):
Диагональные элементы $N_{\alpha\alpha}$ - это число верных предсказаний модели. Ниже приведен пример $N_{\alpha\beta}$ для трёх классов. Реальное число объектов каждого класса равно 11, 14, 12. Лучше всего модель предсказывает первый класс (первый стролбик - только одна ошибка), хуже всего - третий (последний столбик): $$ N_{\alpha\beta} ~=~ \overbrace{ \begin{array}{|c|c|c|} \hline 10 & 0 & 0 \\ \hline 1 & 11 & 4 \\ \hline 0 & 3 & 8 \\ \hline \end{array} }^{\displaystyle\text{actual}} \left. \phantom{ \begin{array}{c} \\ \\ \\ \end{array} } \right\}\text{predicted} $$
Сумма по столбцам равна числу примеров данного класса $N_\alpha$ (по строчкам - их число по предсказаниям модели): $$ N_\beta = \sum_{\alpha} N_{\alpha\beta} ~-~\text{число примеров класса $\beta$},~~~~~~~~~~~~~~N = \sum_{\alpha,\beta} N_{\alpha\beta} ~-~\text{всего примеров}. $$ Степень "одинаковости" частот $n_\alpha=N_\alpha/N$ примеров различных классов характеризует относительная энтропия $H$, лежащая в интервале [0...1]. Чем она ближе к единице, тем лучше сбалансированы примеры по $C$ классам: $$ H = -\sum_{\alpha} n_\alpha\,\log n_\alpha/\log C $$
По аналогии с бинарной классификацией можно ввести метрики точности (precision) и полноты (recall, она же аккуратность) для каждого класса $\alpha$: $$ P_\alpha = \frac{N_{\alpha\alpha}}{\sum_\beta N_{\alpha\beta}},~~~~~~~~~~~R_\alpha=\frac{N_{\alpha\alpha}}{N_\alpha} $$ и их средние значения по всем классам: $$ \text{Precision} = \frac{1}{C}\sum^{C-1}_{\alpha=0} P_\alpha,~~~~~~~~~~~~~ \text{Recall} = \frac{1}{C}\sum^{C-1}_{\alpha=0} R_\alpha,~~~~~~~~~~~~ \text{Accuracy} = \frac{\sum_\alpha N_{\alpha\alpha}}{N} $$ Приведём пример вычисления различных метрик при помощи Numpy:
cm = np.array([[100, 5, 0], # матрица ошибок
[ 9, 50, 5],
[ 0, 0, 1]])
N = cm.sum() # 170 число примеров
n = cm.sum(axis=0)/N # [0.641 0.324 0.035] частоты классов
H = -(n*np.log(n)).sum()/np.log(cm.shape[0]) # 0.699 энтропия/log(C)
A = np.trace(cm)/N # 0.888 аккуратность
P = (np.diag(cm)/cm.sum(axis=1)).mean() # 0.911 точность
R = (np.diag(cm)/cm.sum(axis=0)).mean() # 0.664 полнота
Возможна ситуация, когда один класс очень плохо предсказывается: $R_{\alpha}\sim 0$ и теряется в верных предсказаний других классах. В этом случае можно вычислить относительную энтропию нормированных полнот по всем классам, которая характеризует степень "одинаковости" этих полнот (аккуратностей каждого класса): $$ \text{HR} = -\sum_\alpha r_\alpha \log\,r_\alpha/\log C,~~~~~~~~~~~~~~~~~~~r_\alpha=\frac{ R_\alpha }{\sum_\beta R_\beta}. $$
Так, для примера выше:r = np.diag(cm)/cm.sum(axis=0) r = r/r.sum() HR = -(r*np.log(r)).sum()/np.log(cm.shape[0]) # 0.773
В любом случае, наиболее детальная информация о качестве работы модели находится в матрице ошибок.
Метод K-ближайших соседей
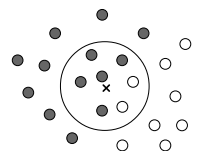 Не все модели являются дифференцируемыми функциями своих параметров.
Рассмотрим, например, метод K-ближайших соседей в котором
вместо обучения, запоминается вся тренировочная выборка (она выступает в качестве "параметров"
модели).
При классификации данного объекта $\mathbf{x}$
изучают его непосредственное окружение в обучающей выборке и на его основании делают
вывод о принадлежности примера к тому или иному классу, например,
выбирают класс ближайшего соседа.
Понятно, что качество метода существенно зависит от правильного выбора
функции расстояния $d(\mathbf{x},\mathbf{x}')$ между двумя точками в пространстве признаков.
Не все модели являются дифференцируемыми функциями своих параметров.
Рассмотрим, например, метод K-ближайших соседей в котором
вместо обучения, запоминается вся тренировочная выборка (она выступает в качестве "параметров"
модели).
При классификации данного объекта $\mathbf{x}$
изучают его непосредственное окружение в обучающей выборке и на его основании делают
вывод о принадлежности примера к тому или иному классу, например,
выбирают класс ближайшего соседа.
Понятно, что качество метода существенно зависит от правильного выбора
функции расстояния $d(\mathbf{x},\mathbf{x}')$ между двумя точками в пространстве признаков.
При наличии шума лучше взять не один, а K ближайших соседей $d(\mathbf{x},\mathbf{x}_1)\le d(\mathbf{x},\mathbf{x}_2)\le...\le d(\mathbf{x},\mathbf{x}_K)$ и использовать класс, встречающийся чаще всего (голосование). Другая разновидность метода состоит в использовании соседей, попавших внутрь сферы радиуса R. Число K или радиус R являются гиперпараметрами метода.
Подбор гиперпараметров можно проводить методом LOO (leave-one-out). Для этого метод соседей применяется по-очереди к каждому объекту обучающей выборки (текущий объект в составе своих соседей, естественно, не учитывается). Выбирается то значение гиперпараметра, для которого аккуратность распознавания класса наибольшая.
Тренировка, тестирование и валидация
Как уже упоминалось, подбор параметров модели неободимо проводить на тренировочных данных (минимизируя функцию ошибки), а проверять аккуратность работы на тестовых данных. В общем случае данные разбивают на три множества: тренировочное (train), валидационное (validation) и тестовое (test):

На валидационном множестве происходит проверка данной модели на переобученность. Если для тренировочных данных ошибка падает, критерии аккуртности растут, а на валидационных данных - всё наоброт, то необходимо уменьшать число параметров или менять модель. Тестовые данные в этих итерациях по подбору модели и её тренировке не участвуют. Они служат для оценки качества работы финальной модели.
Валидационные данные могут также служить для подбора гиперпараметров модели. Существует несколько способов разделения данных на тренировочное и валидационное множества. При простом разбиении исходные объекты случайно перемешиваются и некоторая их доля (например 25%) объявляется валидацией.
Более общим способом является кросс-валидация (cross-validation). Данные для обучения разбиваются на q примерно одинаковых блоков. Сначала в качестве валидации выбирается первый блок, а остальные используются для тренировки. Затем валидацией выступает второй блок и т.д.
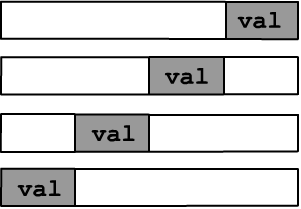
Эту процедуру можно повторить t-раз, случайно перемешивая данные, что называется методом (t x q) - fold cross-validation. Аккуратность модели усредняется по всем блокам и повторам. Метод leave-one-out является частным случаем, когда t=1, q=N-1, где N - число примеров.
Конструирование признаков
Если признаки, характеризующие объект, выбраны верно, задача машинного обучения становится тривиальной. Приведём классический пример. Ниже в двумерном пространстве признаков необходимо классифицировать два класса (квадраты и круги). На левом рисунке признаки являются декартовыми координатами $\{x_0,x_1\}$, а поверхностью, разделяющей классы служит окружность: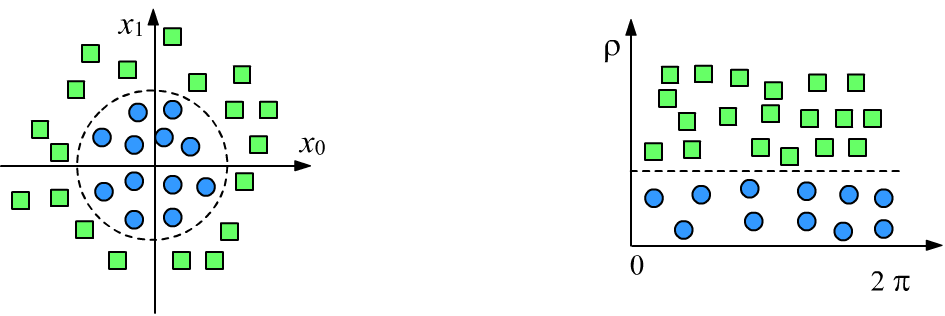
В своё время большие усилия были направлены на поиск различных способов конструирования хороших признаков у объектов. Сейчас считается, что это не обязательно делать и глубокие нейронные сети в процессе обучения "сами" формируют на своём последнем слое наиболее эффективное описание объектов.
Несмотря на очевидные успехи этого подхода,
подготовка хороших признаков обучению модели не вредит.
В частности, обычно стоит хотя бы нормализовывать
входные данные.
Для этого по каждому признаку вычисляется его среднее $\bar{x}_\alpha$ по всем примерам
и дисперсия $\sigma^2_\alpha$ и переходят к новым признакам:
$$
x_{i\alpha} \mapsto \frac{x_{i\alpha}- \bar{x}_\alpha}{\sigma_\alpha},~~~~~~~~~~~~~~~~\bar{x}_\alpha=\frac{1}{N}\sum^{N-1}_{i=0} x_{i\alpha},~~~~~~~~
\sigma^2_\alpha =\frac{1}{N-1}\sum^{N-1}_{i=0}(x_{i\alpha}-\bar{x}_\alpha)^2.
$$
Таким образом нормализованные признаки будут иметь одинаковый масштаб, что может упростить обучение.
В заключение напомним старую притчу:
Однажды Джед и Нед захотели различать своих лошадей. Джед сделал на ухе лошади царапину. Но лошадь Неда поцарапала о колючку тоже самое ухо. Тогда Нед прицепил голубой бант на хвост своей лошади, но лошадь Джеда его сожрала. Фермеры долго размышляли и выбрали признак, который не так легко изменить. Они тщательно измерил высоту лошадей, и оказалось, что черная кобыла Джеда на один сантиметр выше белого жеребца Неда.
