ML: Embedding слов

Введение

Перечислим в словаре $\mathcal{V}$ (vocabulary) размером V_DIM = V все значения некоторого качественного признака. Например, для 7 цветов {red, green, blue, yellow, cyan, magenta, gray} в словаре будет V = 7 слов.
Чтобы нейронная сеть могла работать с таким признаком, его необходимо векторизовать. Это означает, что значениям признака ставятся в соответствие уникальные векторы с E_DIM = E компонентами. Тем самым качественный признак как-бы погружается (embedding) в вещественное векторное пространство. Каждое значение признака - это точка E-мерного пространства. Координаты точки-признака (как вещественные числа), можно отправлять на вход нейронной сети или любой другой модели машинного обучения.

При небольшом количестве значений признака подходит one-hot кодирование. В этом способе размерности векторов и число слов в словаре совпадают (E = V), а вектор i-того слова состоит из нулей, кроме i-той позиции в которой стоит единица. One-hot кодировку можно интерпретировать как V-мерное пространство, каждая ось которого означает наличие (1) или отсутствие (0) данного значения. При этом векторы всех слов словаря попарно ортогональны: 

Vocabulary      One-hot                Embedding
------------------------------------------------------
1. red        [1, 0, 0, 0, 0, 0, 0]    [1.0, 0.0, 0.0]
2. green      [0, 1, 0, 0, 0, 0, 0]    [0.0, 1.0, 0.0]
3. blue       [0, 0, 1, 0, 0, 0, 0]    [0.0, 0.0, 1.0]
4. yellow     [0, 0, 0, 1, 0, 0, 0]    [1.0, 1.0, 0.0]
5. cyan       [0, 0, 0, 0, 1, 0, 0]    [1.0, 0.0, 1.0]
6. magenta    [0, 0, 0, 0, 0, 1, 0]    [0.0, 1.0, 1.0]  
7. gray       [0, 0, 0, 0, 0, 0, 1]    [0.2, 0.2, 0.2]

One-hot кодировку иногда используют и для слов естественного языка, имеющего очень большой словарь.
Любой документ можно охарактеризовать суммой (или логическим OR) one-hot векторов его слов. Такой вектор документа называется мешком слов (bag of words, BoW), т.к. он отражает только количество или факт наличия (при OR) слов в документе, но не их порядок. Подобную простую векторизацию документов можно использовать, например, для их классификации или поиска.

У one-hot кодирования есть два недостатка: 1) при большом словаре векторное представление признаков становится очень громоздким, а число параметров модели увеличивается; 2) one-hot векторы не отражают близости различных слов словаря (если она существует).

Для устранения этих недостатков используют векторы относительно небольшой размерности с вещественными компонентами. Большинство их компонент отличны от нуля, поэтому это распределённое ("размазанное") представление (distributes representation). Такой подход называется Embedding или Word2Vec. Значения компонент векторов обычно определяют в процессе обучения. Предполагается, что векторы в E-мерном пространстве будут объединяться в кластеры по семантической (смысловой) близости слов, что упрощает обучение других слоёв модели. Впрочем, они могут быть и заданы (выше - это {R,G,B}-компоненты цвета).

Для экспериментов с векторизацией слов естественного языка потребуется некоторый корпус текстов. Будем использовать короткие истории ROC Stories, подробное описание которых можно найти в документе NLP_ROCStories.html. Приведенные примеры на библиотеке PyTorch находятся в ноутбуке NN_Embedding_Learn.ipynb, для которого необходимы тексты из файла 100KStories.csv. Слегка почищенные истории можно скачать у нас на сайте

Векторы контекста

С каждым словом $w_i$ словаря $\mathcal{V}$ мы хотим связать вектор $\mathbf{u}_i=\{u_{i0},...,u_{i,\text{E}-1}\}$ так, чтобы семантически близкие слова имели схожие векторы. В результате этого, например, слова dog, cat, rabbit в векторном пространстве должны оказаться рядом (образовать кластер) и при этом быть в отдалении от кластера слов car, bus, train.

Семантическая близость двух слов приводит к тому, что в текстах они встречаются в одинаковом контексте, т.е.в среднем их окружают одни и те-же слова. Возмём вначале векторы размерностью E_DIM, которая равна числу слов V_DIM в словаре (E=V). Пусть у вектора i-го слова j-я компонента пропорциональна частоте $u_{ij} = P(w_i,w_j)$ совместного появления слов $w_i$ и $w_j$ в одном предложении. Близкие по смыслу слова могут и не встречаться в одном предложении, но они имеют аналогичный контекст и схожие векторы. Ниже красным цветом условно отмечены высокие значения $P(w_i,w_j)$. Видно, что векторы cat и dog похожи и отличаются от векторов car и bus:

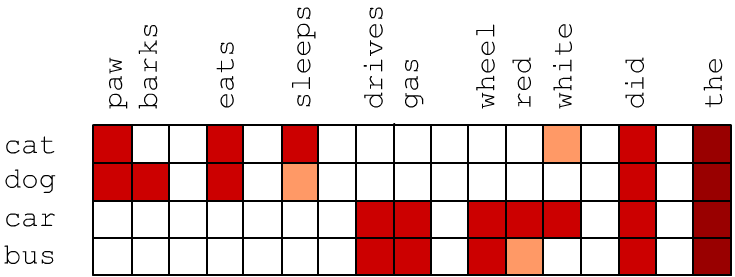
Частоты совместного появления слов в естественном языке "зашумляются" частыми словами типа артикля 'the' (закон Ципфа). Чтобы уменьшить этот эффект, вместо частоты будем использовать метрику pPMI (positive pointwise mutual information): $$ \mathrm{pPMI} = \max(0,\,\mathrm{PMI}),~~~~~~~~~~~~\mathrm{PMI} = \log \frac{P(w_1, w_2)}{P(w_1)P(w_2)} ~\equiv~ \log \frac{P(w_1\,|\,w_2)}{P(w_1)}. $$ Если слова $w_1$ и $w_2$ "независимы", то условная вероятность $P(w_1\,|\,w_2)=P(w_1)$, а для совместной вероятности $P(w_1, w_2) \,=\, P(w_1)P(w_2)$. В этом случае $\mathrm{PMI}=0$. Функция $\max$ в определении pPMI обрезает нулевые значения совместных вероятностей и возможные отрицательные значения логарифма, если $P(w_1\,|\,w_2) < P(w_1)$.

Приведём один из вариантов вычисления совместной вероятности появления двух слов в предложении, при помощи библиотеки numpy. Загрузка списка документов docs (ROC историй) и составление словаря wordID описаны в документе ROC Stories. 

import numpy as np

p12 = np.zeros((V_DIM, V_DIM))                   # совместные вероятности
p1  = np.zeros((V_DIM,))                         # частоты слов        

for d in docs:                                   # по документам
    for s in d:                                  # по предложениям документа    
        ws = set(s.split())                      # "словарь" слов предложения        
        for w1 in ws:                                                           
            if w1 in wordID:                     # слово есть в общем словаре
                p1[ wordID[w1]["id"] ] += 1
                for w2 in ws:    
                    if w2 in wordID:
                        p12[ wordID[w1]["id"], wordID[w2]["id"] ] += 1   
                            
p12 /= p12.sum()                                 # нормируем на единицу
p1  /= p1.sum()
Теперь можно вычислить векторы слов по формуле pPMI: 
vecs = p12 / ( p1.reshape((V_DIM,1)) @ p1.reshape((1, V_DIM)) )

vecs[vecs <= 0] = 1                              # нули или минус под логарифмом
vecs = np.log(vecs) 
vecs[vecs <= 0] = 0                              # max в pPMI
Время получения компонент векторов для корпуса 100k ROCStories на Python занимает около минуты (при вычислениях на CPU Intel i7-7500U 2.7GHz, 16Gb). Приведём примеры нескольких компонент четырёх векторов (опуская нули): 
         paws       vet     wheel      driver   motion     white      very      we        can 
     bark     collar    claw       gas      stops      red       the       after    not        to   
    ------------------------------------------------------------------------------------------------     
cat  1.1  4.0  2.6  2.9  2.5                                1.6  0.4  0.3       0.1            
dog  3.7  2.9  3.3  3.0                      0.2            1.1  0.4       0.1            0.1 

car                           1.5  2.2  2.0  1.5       1.3       0.3            0.1            0.1 
bus                                     3.8  2.7  2.6            0.8       0.5  0.4            0.3    

say  2.7                                0.5                 0.5                 0.4  1.1  1.3  0.8 
ask                                1.7       2.1                                     0.2  1.1  1.1 
get                 0.9       0.8  1.0       0.9  1.2                           0.3  0.7  0.7  1.0

Обратим внимание на малые значения pPMI с высокочастотными словами в последних колонках таблицы. Очевидно, что эти слова не имеют прямой смысловой связи со словами cat, dog, cat, bus.

Понижение размерности

Хотя компоненты векторов слов теперь отражают сходство слов, их размерность так-же велика, как и при one-hot кодировке. Для понижения размерности эмбединга, воспользуемся методом главных компонент (PCA: principal component analysis): 

from   sklearn.decomposition import PCA

pca = PCA()
res = pca.fit_transform(vecs)
Вычисление главных компонент для матрицы (10000, 10000) занимает около 7 минут. Первые 50 собственных значений ковариационной матрицы (pca.singular_values_) быстро убывают, а потом убывание к нулю (при i=V) становится практически линейным:

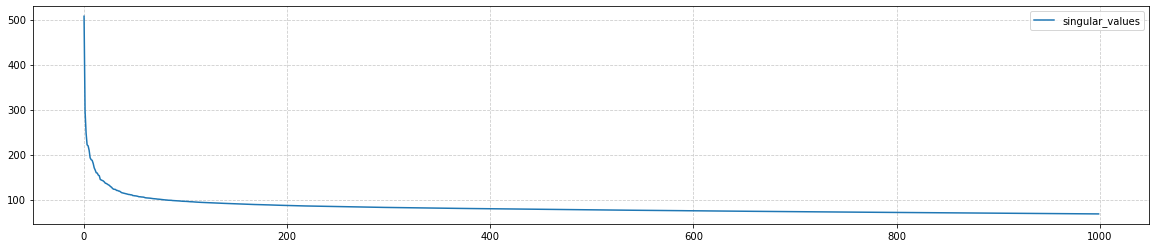
Ограничимся далее размерностью векторного пространства E_DIM = E = 100: 

vecs = res[:, : E_DIM]                                           # первые 100 колонок
vecs = (vec-vec.mean(axis=0))/(res.std(axis=0) * np.sqrt(E_DIM) )# выравниваем разброс
Финальная нормализация компонент (вычитание среднего и деление на разброс) переносит "центр облака точек" в начало координат, что улучшает работу косинусной меры расстояния (см. ниже). Деление на корень от размерности эмбединга E_DIM, масштабирует длины векторов в среднем к единичному значению.

Меры близости

Меры близости двух векторов $\mathbf{u}$, $\mathbf{v}$ в многомерном пространстве можно выбрать различным образом: $$ \begin{array}{llclcl} \text{евклидово расстояние:} & \text{dist}_1(\mathbf{u},\mathbf{v}) &=& \sqrt{(\mathbf{u}-\mathbf{v})^2}\\[2mm] \text{косинусное расстояние:} & \text{dist}_2(\mathbf{u},\mathbf{v}) &=& 1-\cos(\mathbf{u},\mathbf{v})&=& 1-\displaystyle \frac{\mathbf{u}\mathbf{v}}{|\mathbf{u}|\cdot|\mathbf{v}|} \end{array} $$ После сокращения размерности чаще используют косинусное расстояние. При помощи косинусного расстояния найдём ближайших соседей к некоторым словам (см. модуль my_embedding.py):

Для сравнения косинусное и евклидово расстояние между этими словами: 

                        dist_cos                                              dist_len
       cat    car  apple gin  monday red   small say        cat    car  apple gin  monday red   small say     
cat          0.94  1.01  0.90  1.07  1.02  0.84  1.01             2.62  2.62  1.98  2.27  3.06  2.46  2.32
car    0.94        0.97  1.07  1.06  0.87  1.02  1.02       2.62        2.57  2.10  2.26  2.83  2.73  2.33
apple  1.01  0.97        0.99  0.94  0.84  0.94  1.03       2.62  2.57        1.90  2.02  2.70  2.51  2.22
gin    0.90  1.07  0.99        1.16  0.90  1.01  1.09       1.98  2.10  1.90        1.40  2.38  2.03  1.53
monday 1.07  1.06  0.94  1.16        0.89  1.09  1.15       2.27  2.26  2.02  1.40        2.48  2.27  1.81
red    1.02  0.87  0.84  0.90  0.89        0.98  1.05       3.06  2.83  2.70  2.38  2.48        2.98  2.73
small  0.84  1.02  0.94  1.01  1.09  0.98        1.04       2.46  2.73  2.51  2.03  2.27  2.98        2.33
say    1.01  1.02  1.03  1.09  1.15  1.05  1.04             2.32  2.33  2.22  1.53  1.81  2.73  2.33
Обратим внимание, что косинусное расстояние между словами из "разичных кластеров" порядка единицы, что говорит о перпендикулярности этих векторов.

По сравнению с подходами, основанными на нейронных сетях, векторизация при помощи на PCA достаточно быстрый метод и при относительно небольших словарях может служить очень неплохим первым приближением.

Свойства векторного пространства

Построим гистограммы распределения длин векторов по отдельности для частых слов (первые 1000), редких слов и всех вместе. Частые слова имеют более длинные векторы, что типично для всех методов эмбединга: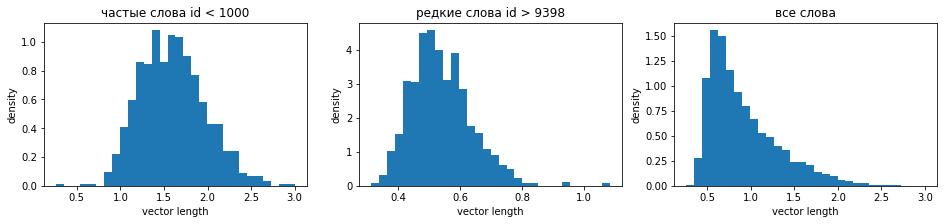
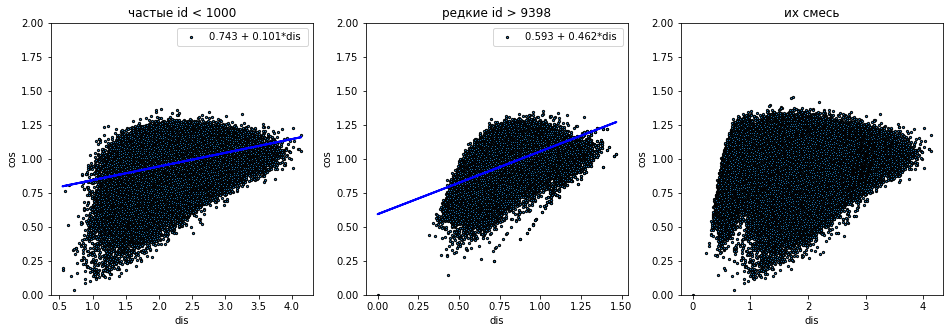
Построим также зависимость евклидового расстояния (корень из суммы квадратов) от косинусного $1-\cos$ для первых 1000 и последних 1000 (по частотности) слов:
Заметим, что ярко-выраженной линейной зависимости нет. Аналогичная диаграмма для трёх кластеров (косинусное расстояние вычислено относительно центра кластера, равного среднему вектору его слов):

Семантические направления

Вычислим вектор разности между векторами двух слов $\mathbf{u}_1-\mathbf{u}_2$. Приведём его длину len и матрицу косинуснусных расстояний между такими векторами (если они меньше 1, то угол между векорами меньше 90°): 
        sex                   pm          len      1      2      3      4      5      6      7
1. [he          she    ]   23352 - 19702| 0.63|        0.56   0.60   0.44   0.68   0.71   0.84  
2. [man         woman  ]    1020 -   311| 1.35| 0.56          0.57   0.74   0.84   0.91   0.75  
3. [boy         girl   ]     378 -   551| 1.18| 0.60   0.57          0.78   0.85   0.77   0.76  
4. [father      mother ]     319 -   744| 1.43| 0.44   0.74   0.78          0.64   1.06   1.13  
5. [uncle       aunt   ]      68 -    76| 1.34| 0.68   0.84   0.85   0.64          0.95   1.10  
6. [nephew      niece  ]      38 -    65| 1.18| 0.71   0.91   0.77   1.06   0.95          0.87  
7. [king        queen  ]      29 -    17| 1.00| 0.84   0.75   0.76   1.13   1.10   0.87
Заметно хуже ось возраста: 
         age               pm             len      1      2      3      4      5
1. [old          young ]     778 -   175| 2.23|        0.99   0.93   1.05   1.09  
2. [man         boy    ]    1020 -   378| 1.81| 0.99          0.32   0.94   0.92  
3. [woman       girl   ]     311 -   551| 1.58| 0.93   0.32          0.97   0.94  
4. [grandpa     dad    ]      56 -   568| 1.54| 1.05   0.94   0.97          0.66  
5. [grandmother mother ]     120 -   744| 1.45| 1.09   0.92   0.94   0.66

Немного математики $^*$

Напомним, что метод PCA в $n$-мерном пространстве ищет "ближайшую" к обучающим точкам $m$-мерную плоскость, для которой средне-квадратичное отклонение расстояний множества точек минимально.
Kоординаты $N$ точек в $n$-мерном пространстве определяются матрицей $\mathbf{X}$ формы $(N,n)$. Пусть из координат вычтены их средние значения по всем точкам. Тогда ковариационная матрица равна $\mathbf{C} = \mathbf{X}^\top\mathbf{X}/(N-1)$.

Решение PCA-задачи сводится к нахождению отсортированных в порядке убывания $\lambda_1 \ge ... \ge \lambda_n$ собственных значений $\lambda_\alpha$ ковариационной матрицы: $\mathbf{C}\,\mathbf{v}^{(\alpha)}=\lambda_\alpha\,\mathbf{v}^{(\alpha)}.$ Пусть $\mathbf{L}=\text{diag}(\lambda_1,...\lambda_n)$ - диагональная матрица. Тогда $\mathbf{C}=\mathbf{V}\mathbf{L}\mathbf{V}^\top$, где в каждой колонке матрицы $\mathbf{V}_{i\alpha}=v^{(\alpha)}_i$ находятся компоненты собственных векторов $\mathbf{v}^{(\alpha)}.$ Первые $m$ колонок матрицы $\mathbf{X}\mathbf{V}$ формы $(N,n)$ будут координатами проекций точек $\mathbf{X}$ на $m$-мерную плоскость.

При нахождении $\mathbf{C}$, перемножение больших матриц $\mathbf{X}$ формы $(N,n)$ приводит к потери точности. Поэтому иногда эффективнее использовать SVD-разложение (singular value decomposition):

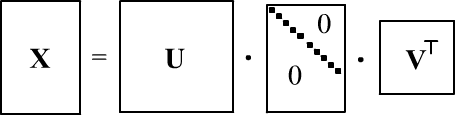
$$ \mathbf{X}=\mathbf{U}\mathbf{S}\mathbf{V}^\top,~~~\text{с матрицами форм:}~~~~(N,N)\,(N,n)\,(n,n), $$

где $\mathbf{S}$ - диагональная матрица $(N,n)$ c сингулярными числами $s_i$ на диагонали, а $\mathbf{U}, \mathbf{V}$ - ортогональные матрицы (колонки $\mathbf{U}$ - собственные векторы матрицы $\mathbf{X}\mathbf{X}^\top$, а колонки $\mathbf{V}$ - собственные векторы $\mathbf{X}^\top\mathbf{X}$). Понятно, что

$$ \mathbf{C} = \frac{\mathbf{X}\mathbf{X}^\top}{N-1} = \frac{\mathbf{V}\mathbf{S}\mathbf{U}^\top\,\mathbf{U}\mathbf{S}\mathbf{V}^\top} {N-1} =\mathbf{V}\frac{\mathbf{S}^2}{N-1}\mathbf{V}^\top. $$

Таким образом, собственные значения ковариационной матрицы равны $\lambda_i=s^2_i/(N-1)$, а главные компоненты даются произведением $\mathbf{X}\mathbf{V}=\mathbf{U}\mathbf{S}\mathbf{V}^\top\mathbf{V}=\mathbf{U}\,\mathbf{S}$. На numpy, PCA при помощи SVD делается следующим образом: 

U, S, V = np.linalg.svd(X - X.mean(axis=0)) 
vecs = U[:, : m] @ np.diag(S[ : m])

Global Vectors (GloVe)

При очень больших словарях понижение размерности методом PCA или SVD может быть затруднительно. В этом случае, обычно, используют нейронные сети, которые сразу работают с векторными пространствами небольших измерений (см. следующий документ). В работе Pennington J. et.al. (2014) был предложен промежуточный подход, названный "Global Vectors for Word Representation" или сокращённо GloVe.

В этом подходе сначала вычисляются логарифмы вероятностей $P_{ij}$ совместной встречаемости слов $w_i$ и $w_j$ в тексте внутри скользящего окна из 10 слов. Подбираемыми параметрами модели являются компоненты E-мерных векторов $\mathbf{u}_i$ слов и параметры смещения $b_i$. В процессе обучения (подбора $\mathbf{u}_i$ и $b_i$) минимизируется следующий функционал ошибки:

$$ \text{Loss} = \sum_{ij} f(N_{ij})\,\bigr(\mathbf{u}_i\mathbf{u}'_j + b_i + b'_j - \log P_{ij}\bigr)^2 = \min_{\mathbf{u}_i,\mathbf{u}'_j\,b_i,b'_j} $$ Веса $f(N_{ij})$ пропорциональны числу появления $N_{ij}$ пары в окне. Эти веса обрезаются для слишком высокочастотных слов. Авторы выбрали следующую функцию, в которой $x_\text{max}=100$ независимо (?) от длины текста.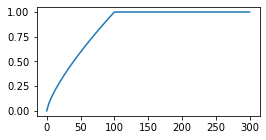 $$ f(x) = \left\{ \begin{array}{ll} (x/x_{\text{max}})^{3/4} & \text{if}~ x < x_{\text{max}}\\ 1 & \text{otherwise} \end{array} \right. $$

В скалярном произведении $\mathbf{u}_i\mathbf{u}'_j$ использовались разные векторы $\mathbf{u}$ и $\mathbf{u}'$, а финальный эмбединг равнялся $\mathbf{u}+\mathbf{u}'$. С точки зрения авторов, это помогало переобучению (хотя $P_{ij}=P_{ji}$, но начальные случайные значения компонент $\mathbf{u}$ и $\mathbf{u}'$ были различными). Параметры "смещений" $b_i$, $b'_j$ можно интерпретировать, как обучаемые вероятности в знаменателе PMI, т.е. минимизируя ошибку мы стремимся получить что-то типа $\mathbf{u}_i\mathbf{u}'_j = \log P_{ij}/P_i P_j$.

Векторизация была проведена на больших корпусах текстов:

We trained our model on five corpora of varying sizes: a 2010 Wikipedia dump with 1 billion tokens; a 2014 Wikipedia dump with 1.6 billion tokens; Gigaword 5 which has 4.3 billion tokens; the combination Gigaword5 + Wikipedia2014, which has 6 billion tokens; and on 42 billion tokens of web data, from Common Crawl

В открытом доступе находятся наборы векторов с размерностью от 50 до 300 и словарём 400k. Перед построением словаря, авторы "tokenize and lowercase each corpus with the Stanford tokenizer". Хорошей идей при использовании GloVe будет также использование Stanford tokenizer, т.к. он делает "непробельное" разбиение: can't → [ca, n't]; she's → [she, 's] и т.п.

Анализ векторного пространства GloVe можно найти в этом документе.

Проблемы эмбединга

Технология эмбединга - одно из самых замечательных изобретений последнего десятилетия. Однако, с ней связан также ряд проблем.

✑ Для получения надёжных контекстных векторов редких слова требуется очень большой корпус текстов. Однако, в большом корпусе может происходить перекос в семантических значениях слов по сравнению с их харатерными обыденными значениями. Например при векторизации GloVe для слова apple получаем следующих ближайших соседей: microsoft(.26), ibm (.32), intel(.32), software(.32), dell (.33). В тоже время существенно меньший корпус ROC Stories выдаёт более "обыденных соседей" для apple.

✑ Простой эмбединг не учитывает семантической и синтаксической неоднозначности. Обычно предполагается, что семантическая неоднозначность снимается, после прохождения исходных векторов слов через несколько слоёв нейронной сети, в которых анализируется контекст всего предложения (архитектуры RNN или Attention). Например, общий контекст предложений "Remove first row of the table." и "Put an apple on the table" позволяет в каждом случае уточнить семантическое значение слова table.

✑ Так как слова в векторном пространстве являются точками, а не протяжёнными областями, эмбединг не отражает иерархической природы смыслов: предмет - инструмент - молоток.