ML: Attention - Механизм внимания
Введение
Механизм Attention (внимание) в настоящее время встречается в самых различных архитектурах и задачах (перевод, генерация текста, аннотация изображений и т.д.). В этом документе мы рассмотрим исторически первое использование Attention в задаче машинного перевода (Bahdanau D., et al., 2014) и реализацию функции многоголового внимания на PyTorch. Следующие документы посвящены применению этого механизма в сети Transformer и её развитию в моделях GPT и BERT.
Основная идея
Прежде чем погрузится в технические детали, рассмотрим идею механизма внимания на примере задачи снятия семантической неоднозначности. При работе с естественным языком, каждому слову в словаре ставится в соответствие вектор с вещественными компонентами (эмбединг слова). Эти векторы поступают на вход нейронной сети с той или иной архитектурой. Компоненты векторов являются параметрами, которые подбираются в процессе обучения так, чтобы близкие по смыслу слова имели схожие векторы. В качестве меры близости обычно выступает косинус угла между векторами, который определяется их скалярным произведением.
Одна из проблем, возникающая при построении эмбедингов слов, - это неоднозначность естественного языка (table - это стол или таблица и т.д.). При обучении на корпусе текстов, вектор эмбединга каждого слова получает фиксированные компоненты, которые не зависят от того смысла, в котором это слово встретилось в тексте.
Механизм внимания (точнее в этом случае самовнимания) модифицирует вектор эмбединга каждого слова, "подмешивая" к нему векторы его окружения (контекста) с некоторыми весами. Пусть, например, в предложении "The table has a lot of data" словам соответствуют векторы $\mathbf{v}_1,...,\mathbf{v}_7$. Для модификации вектора $\mathbf{v}_\text{table}=\mathbf{v}_2$, вычислим его скалярные произведения с другими словами: $\{w_1,w_2,...,w_7\}=\{\mathbf{v}_2\mathbf{v}_1,~\mathbf{v}_2\mathbf{v}_2,~...,\mathbf{v}_2\mathbf{v}_7\}$ (включая его же). Полученные веса отнормируем при помощи функции softmax, так чтобы их сума равнялась единице, а значения лежали в диапазоне $[0...1]$: $$ w'_i = \text{softmax}(w_1,...,w_7) = e^{w_i}/(e^{w_1}+...+e^{w_7}). $$ Чем ближе к единице веса $w'_i$, тем сильнее слово $\mathbf{v}_2$ похоже на слово $\mathbf{v}_i$. Построим теперь новый эмбединг слова table в виде взвешенной суммы: $$ \mathbf{v}'_2 = w'_1\,\mathbf{v}_1+w'_2\,\mathbf{v}_2+...+w'_7\,\mathbf{v}_7. $$ Так как артикли и предлоги в векторном пространстве находятся далеко от векторов table и data, мы получим что-то типа: $$ \begin{array}{llll} \mathbf{v}'_\text{table}\approx 0.9\cdot \mathbf{v}_\text{table}+0.1\cdot \mathbf{v}_\text{data} &~~~~~~~& \text{The table has a lot of data}\\ \mathbf{v}'_\text{table}\approx 0.8\cdot \mathbf{v}_\text{table}+0.2\cdot \mathbf{v}_\text{plate} && \text{There is a plate on the table} \end{array} $$ Для текста с другим контекстом (второй пример выше) получатся иные компоненты. В первом случае "внимание" слова table фокусируется на слове data, а во втором - на слове plate. В результате единый для всех смыслов вектор $\mathbf{v}_\text{table}$ расщепляется на два вектора, которые имеют тенденцию перемещаться к своим смысловым кластерам (row, digits,... в первом случае и chair, furniture, ... - во втором).
Encoder-Decoder
Напомним, что простейшая архитектура Encoder-Decoder состоит из двух различных рекуррентных сетей (энкодера и декодера). Энкодер на вход получает текст на одном языке (source), а декодер должен на выходе выдать перевод - текст на другом языке (target). Последняя RNN-ячейка энкодера на выходе содержит вектор скрытого состояния $\mathbf{h}_e^{\text{last}}$, который "накопил" в себе информацию обо всём source-предложении (context vector). Этот вектор отправляют в качестве начального скрытого состояния в первую RNN-ячейку декодера:
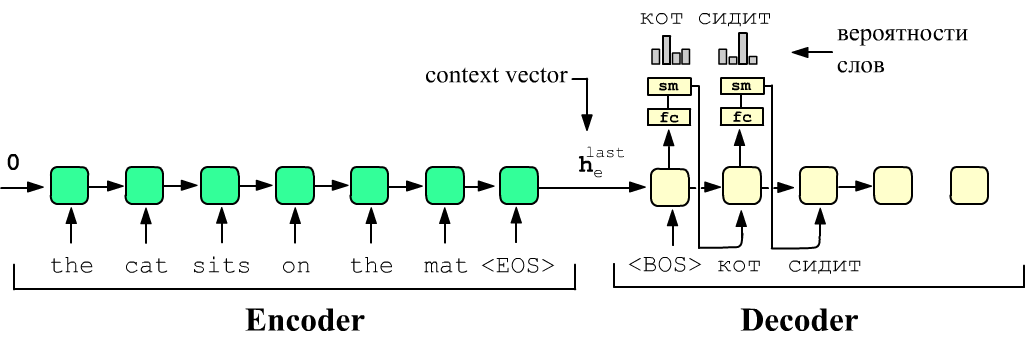
Затем на вход первой ячейки декодера подаётся служебный токен <BOS> (begin of sentence). На выходе этой ячейки сеть обучают выдавать слово-перевод "кот" (см. рисунок). Для этого выходы ячеек пропускают через линейный слой (fc) с числом нейронов равным числу слов в словаре. Затем softmax-функция (sm), выдаёт "вероятности" слов из которых выбирается номер максимальной (argmax). Вектор полученного слова "кот" передаётся на вход второй ячейки и т.д. пока не получится служебный токен <ЕOS> (end of sentence).
Можно также использовать метод принудительного обучения (teacher forcing). В этом случае на все входы декодера сразу подают правильный перевод, а на выходе от него требуют выдать это же предложение сдвинутое на одно слово влево:
<BOS> кот сидит на коврике -> [Decoder] -> кот сидит на коврике <EOS>Обычно между режимами "честного" и "принудительного" обучения производят случайное переключение.
Основная проблема такой архитектуры состоит в том, что при длинных source-предложениях финальное скрытое состояние энкодера "забывает" начало предложения. Частично эту проблему можно решить при помощи двунаправленных RNN. Однако и в этом случае скрытое состояние, поступающее на вход декодера, плохо "помнит" середину source-предложения. Аналогичная проблема возникает в декодере, который со временем "забывает" переданное ему source-предложение (как скрытое состояние последней ячейки энкодера). Снизить проблему можно подмешивая это скрытое состояние в скрытые состояния всех ячеек декодера. Были придуманы и другие трюки по борьбе с длинными предложениями. Однако наиболее эффективным оказался механизм внимания.
Фокус внимания в RNN
Обычно при переводе человек несколько раз просматривает source-предложение, фокусируясь на важных к данному моменту словах и их окружении, снимая тем самым синтаксическую или семантическую неоднозначности. Так, слово "mat" может означать "коврик" или "спортивный мат". Для выдачи правильного перевода необходимо сфокусироваться не только на слове "mat", но и на слове "cat".
Реализация этой идеи состоит в следующем. К очередному скрытому состоянию декодера добавляется взвешенная сумма всех скрытых состояний энкодера. Значения весов в сумме отражают степень важности того или иного слова в source-предложении для генерации текущего слова target-предложения.
Будем обозначать вектор скрытого состояния ячейки энкодера с номером $\alpha$ как $\mathbf{v}_{\alpha}=\{v_{\alpha,0},...,v_{\alpha,E-1}\}$, а декодера как $\mathbf{u}_\alpha=\{u_{\alpha,0},...,u_{\alpha,E-1}\}$, где E - размерность эмбединга. Веса внимания ячейки декодера c номером $\alpha$ на $\beta$-том слове энкодера обозначим как $w_{\alpha\beta}$. В следующую $(\alpha+1)$-ячейку декодера будет отправляться не текущее скрытое состояние $\mathbf{u}_\alpha$, а его сумма со взвешенными скрытыми состояниями энкодера $\mathbf{u}_\alpha +\mathbf{u}'_\alpha$, где: $$ \mathbf{u}'_\alpha = \sum_\beta w_{\alpha\beta} \,\mathbf{v}_\beta,~~~~~~~~~~~\sum_\beta w_{\alpha\beta} = 1,~~~~~~~~~~~ w_{\alpha\beta} = f\bigr(\mathbf{u}_\alpha, \mathbf{v}_\beta \bigr). $$ В качестве функции $f$, вычисляющей веса внимания $w_{\alpha\beta}$, может выступать полносвязный слой или скалярное произведение $\mathbf{u}_\alpha\cdot \mathbf{v}_\beta$ (векторы близких слов параллельны). Ниже на рисунке функция $f$ изображена синим кругом. Сумма весов $w_{\alpha\beta}$ по второму индексу $\beta$ должна равняться единице, что обеспечивает слой softmax. Скрытые состояния $v_\alpha$, как обычно, попадают как на выход (в функцию $f$), так и в следующую ячейку рекуррентного слоя:
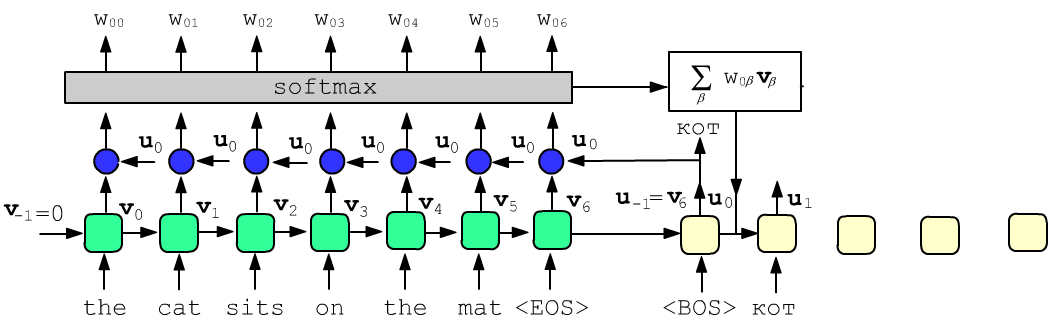
В данном примере вектор скрытого состояния, полученный при подаче служебного слова "<BOS>" (begin of sentence) и последнего скрытого состояния энкодера, должен ближе всего оказаться к векторам первых ячеек энкодера (для однотипных по синтаксису языков). К нему также подмешивается вектор слова sits и с меньшими весами следующие слова исходного предложения. Вторая ячейка декодера, получив на вход вектор слова "кот", должна сфокусироваться на слове "cat" и семантически близких словах ("sits" и т.д.).
Подчеркнём, что source и target языки имеют различные эмбединги. Однако в процессе обучения векторы слов "cat" и кот оказываются близкими, что приводит в увеличению соответствующих весов внимания.
Если функция $f$ пропорциональна скалярному произведению векторов ($\mu=\text{const}$): $$ f(\mathbf{u},\mathbf{v}) = \mu\,\mathbf{u}\cdot\mathbf{v}, $$ то веса внимания к скрытым состояниям декодера определяются следующим образом: $$ w_{\alpha\beta} = \text{softmax}\bigr(\mu\,\mathbf{u}_\alpha\mathbf{v}_\beta\bigr) = \frac{e^{\mu\,\mathbf{u}_\alpha\mathbf{v}_\beta} } {\sum_\gamma e^{\mu\, \mathbf{u}_\alpha\mathbf{v}_\gamma } }. $$
Ещё один вариант функции вычисления весов содержит две матрицы $\mathbf{W}_1$, $\mathbf{W}_2$ и вектор $\mathbf{b}$ (компоненты которых подбирают в процессе обучения): $$ f(\mathbf{u},\mathbf{v}) = \tanh\bigr(\mathbf{u}\cdot\mathbf{W}_1+\mathbf{v}\cdot\mathbf{W}_2\bigr)\,\mathbf{b}. $$
В качестве весов далее будем использовать скалярное произведение $\omega_{\alpha\beta} = \mu\,\mathbf{u}_\alpha\cdot\mathbf{v}_\beta$ и запишем результат действия механизма внимания в матричном виде.
Функция Attention
Пусть есть три матрицы: матрица $\mathbf{Q}$ запросов (query), матрица $\mathbf{K}$ ключей (key) и матрица $\mathbf{V}$ значений (value). Введенные матрицы являются аргументами функции внимания: $$ \mathbf{A} = \text{Attn}( \mathbf{Q},\, \mathbf{K},\, \mathbf{V}) ~=~ \text{softmax} \Bigr(\frac{\mathbf{Q}\cdot\mathbf{K}^\top}{\sqrt{E}}\Bigr)\,\mathbf{V}, $$ где $\top$ - операция транспонирования, переставляющая местами индексы матрицы и функция softmax независимо применяется к каждой строке матрицы $\mathbf{Q}\cdot\mathbf{K}^\top/\sqrt{E}$. В общем случае матрицы могут иметь следующие формы: $$ \mathbf{Q}:~~~(N,\,E),~~~~~~~~~~~\mathbf{K}:~~~(M,\,E),~~~~~~~~~~~\mathbf{V}:~~~(M,\,E'),~~~~~~~~~~~\mathbf{A}:~~~(N,\,E'). $$
Названия введенных матриц связаны с простой моделью ассоциативной памяти. Будем считать, что в памяти хранится $M$ пар векторов ключ-значение: $(\mathbf{k}_1,\mathbf{v}_1)$,...., $(\mathbf{k}_M,\mathbf{v}_M)$. Они являются строками матриц $\mathbf{K}$ и $\mathbf{V}$, имея, вообще говоря, различные размерности $E$ и $E'$. Пусть матрица запроса $\mathbf{Q}$ состоит из одной строки ($N=1$) - вектора $\mathbf{q}$ размерности $E=2$ и есть $M=3$ ключа $k_{\alpha i}$ (первый индекс - номер ключа, второй - номер его компоненты). Тогда: $$ \mathbf{Q}\,\mathbf{K}^\top ~=~ \begin{array}{|c|c|} \hline q_0 & q_1 \\ \hline \end{array} \cdot \begin{array}{|c|c|} \hline k_{00} & k_{00} \\ \hline k_{10} & k_{10} \\ \hline k_{20} & k_{20} \\ \hline \end{array}^{~\top} ~=~ \begin{array}{|c|c|} \hline q_0 & q_1 \\ \hline \end{array} \cdot \begin{array}{|c|c|c|} \hline k_{00} & k_{10} & k_{20}\\ \hline k_{01} & k_{11} & k_{21}\\ \hline \end{array} ~=~ \begin{array}{|c|c|} \hline \mathbf{q}\mathbf{k}_0 & \mathbf{q}\mathbf{k}_1 & \mathbf{q}\mathbf{k}_2\\ \hline \end{array} $$ Если вектор запроса $\mathbf{q}$ параллелен $i$-тому ключу $\mathbf{k}_i$ и антипараллелен остальным ключам $\mathbf{q}\mathbf{k}_j \ll -1$, $j\neq i$, то софтмакс вернёт вектор из нулей, кроме $i$-й позиции, где будет стоять 1. Соответственно, функция Attn вернёт значение $\mathbf{v}_i$ из $i$-той пары. В общем случае, если точного совпадения ключа и запроса нет, то возвращается взвешенная сумма с преобладанием значений, ключи которых наиболее похожи (со-направлены) запросу.
В соответствии с формами матриц $\mathbf{Q},\,\mathbf{K}$, аргументом функции softmax выступает матрица формы $(N,M)$, т.к. $(N,E) \cdot (M,E)^\top= (N,E) \cdot (E,M) = (N,M)$. Функция softmax, применённая к каждой строчке этой матрицы (по размерности $M$), даёт матрицу $\Omega_{ij}$ той же формы. Сумма её элементов по второму индексу $j$ равна единице для каждого $i$. Эта матрица сворачивается с $\mathbf{V}$, поэтому результатом действия функции будет матрица формы $(N,\,E')$. Если $N > 1$, то функция $\text{Attn}$ одновременно обрабатывает несколько запросов (строк матрицы $\mathbf{Q}$).
☝ Матрица, обратная к матрице $\mathbf{A}$, обозначается как $\mathbf{A}^{-1}$, Матричное произведение $\mathbf{Q}\cdot\mathbf{K}^\top$ запросов и ключей, следуя Vaswani A., et al. (2017), принято делить на корень из размерности $E$ векторов матриц $\mathbf{Q}$ и $\mathbf{K}$. Мотивация для этого может быть следующей. Пусть компоненты двух векторов $\mathbf{q}$ и $\mathbf{k}$ являются независимыми случайными величинами с нулевым средним и единичной дисперсией. Тогда скалярное произведение $\mathbf{q}\cdot\mathbf{k}$ также имеет нулевое среднее и дисперсию равную размерности векторов $E$, т.е. типичные значения $\mathbf{q}\cdot\mathbf{k}$ находятся в интервале $\pm\sqrt{E}$. Масштабирование переводит их к интервалу $\pm 1$.
Вернёмся теперь к механизму внимания, описанному в предыдущем разделе. Пусть $\mathbf{U}= u_{\alpha i}$ - векторы скрытых состояний декодера, а $\mathbf{V}= v_{\alpha i}$ - энкодера, где первый индекс - номер вектора, а второй - его компоненты (каждая строчка матриц $\mathbf{U}$ и $\mathbf{V}$ это $\alpha$-тый вектор). Тогда, компоненты векторов $\mathbf{u}'_\alpha$ - добавок к скрытому состоянию декодера являются строками матрицы ($\mu = 1/\sqrt{E}$): $$ \mathbf{U}' = \text{Attn}( \mathbf{U},\, \mathbf{V}, \, \mathbf{V}). $$ В этом случае $M$ - число ячеек энкодера ( = числу слов входного предложения = пар ключ-значение), а $N=1$ (одно слово текущей ячейки декодера).
Реализация функции Attn на PyTorch имеет следующий вид (B - число примеров в батче, E - размерность эмбединга, N - число запросов; M число пар ключ-значение):
import math
import torch
import torch.nn as nn
def Attn(Q, K, V): # Q: (B,N,E); K,V: (B,M,E)
E = Q.size(-1) # размерность эмбединга E
W = torch.bmm(Q, K.transpose(-2, -1)) / math.sqrt(E) # (B,N,M)
W = nn.functional.softmax(W, dim = -1) # по последнему индексу тензора
return torch.bmm(W, V) # (B,N,E)
Метод bmm перемножает две матрицы: bmm( (B,N,E), (B,E,M) ) = (B,N,M) независимо для каждого примера в батче, т.е. в "цикле" по примерам B обычным образом умножает: (N,E) @ (E,M) = (N,M).
Самовнимание
Механизм внимания можно применять не только в архитектуре энкодер-декодер. Рассмотрим, например, проблему неоднозначности смысла слов, упомянутую в начале документа. Пусть есть простая архитектура сети с $N$ входами и $N$ выходами. На её входы поступают $N$ слов (в виде $E$-мерных векторов эмбединга), а на выходах должны получиться изменённые векторы этих же слов, с учётом контекста всего предложения.
Пусть матрица $\mathbf{V}$ размерности $(N,E)$ в $N$ строчках содержит $N$ векторов слов предложения. Вычислим значение функции $\text{Attn}(\mathbf{V},\, \mathbf{V},\,\mathbf{V})$. Так как матрица запроса совпадает с матрицами ключей и значений, эта ситуация называется само-вниманием (self-attention). Распишем матричные умножения в явном виде, например, для $N=3$ и $E=2$ (в матрице $\mathbf{V}:~v_{\alpha i}$, где, как и раньше, первый индекс - это номер слова, второй - номер компоненты его вектора): $$ \mathbf{V}\cdot\mathbf{V}^\top ~=~ \begin{array}{|c|c|} \hline v_{00} & v_{01} \\ \hline v_{10} & v_{11} \\ \hline v_{20} & v_{21} \\ \hline \end{array} \cdot \begin{array}{|c|c|} \hline v_{00} & v_{10} & v_{20} \\ \hline v_{01} & v_{11} & v_{21} \\ \hline \end{array} = \begin{array}{|c|c|c|} \hline \mathbf{v}_0\mathbf{v}_0 & \mathbf{v}_0\mathbf{v}_1 & \mathbf{v}_0\mathbf{v}_2 \\ \hline \mathbf{v}_1\mathbf{v}_0 & \mathbf{v}_1\mathbf{v}_1 & \mathbf{v}_1\mathbf{v}_2 \\ \hline \mathbf{v}_2\mathbf{v}_0 & \mathbf{v}_2\mathbf{v}_1 & \mathbf{v}_2\mathbf{v}_2 \\ \hline \end{array} $$ В первой строке результирующей матрицы находятся скалярные произведения вектора $\mathbf{v}_0$ первого слова со всеми остальными словами предложения. Во второй - аналогичные произведения второго слова $\mathbf{v}_1$ и т.д. Наибольшие (положительные) значения обычно имеют диагональные элементы матрицы $\mathbf{v}^2_0$, $\mathbf{v}^2_1$, $\mathbf{v}^2_2$ (при сравнимых длинах векторов). После вычисления (построчного) функции софтмакса получится что-то типа: $$ \text{Attn}(\mathbf{V},\, \mathbf{V},\,\mathbf{V}) ~=~ \text{softmax}\Bigr(\frac{\mathbf{V}\cdot\mathbf{V}^\top}{\sqrt{2}}\Bigr)\cdot\mathbf{V} ~=~ \begin{array}{|c|c|c|} \hline 0.8 & 0.2 & 0 \\ \hline 0.3 & 0.7 & 0 \\ \hline 0.1 & 0 & 0.9 \\ \hline \end{array} \cdot \begin{array}{|c|c|} \hline v_{00} & v_{01} \\ \hline v_{10} & v_{11} \\ \hline v_{20} & v_{21} \\ \hline \end{array} ~=~ \begin{array}{|l|l|} \hline 0.8\,v_{00} + 0.2\,v_{10} & 0.8\,v_{01} + 0.2\,v_{11} \\ \hline 0.7\,v_{10} + 0.3\,v_{00} & 0.7\,v_{11} + 0.3\,v_{01} \\ \hline 0.9\,v_{20} + 0.1\,v_{00} & 0.9\,v_{21} + 0.1\,v_{01} \\ \hline \end{array} $$ Таким образом, для трёх слов на выходе получаем три исходных вектора к которым "подмешаны" компоненты близких по смыслу слов окружения (если эмбединг был удачно построен).
Многоголовый Attention
Следующим этапом развития технологии Attention, стало введение нескольких обучаемых фокусов внимания на "различных аспектах" последовательности ключей. Напомним, что в свёрточных сетях число вторичных признаков увеличивают, добавляя на очередном уровне анализа изображения дополнительные фильтры. Аналогично, при обработке последовательностей, вводят H фокусов внимания, которые называют головами (каждая голова "смотрит в свою сторону"): $$ \mathbf{A}~=~\text{MultiHead}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{Concat}(\mathbf{h}_1,\dots,\mathbf{h}_H)\,\mathbf{W}^O, ~~~~~~~~~~~\mathbf{h}_i = \text{Attn}(\mathbf{Q}\,\mathbf{W}_i^Q,~ \mathbf{K}\,\mathbf{W}_i^K,~ \mathbf{V}\,\mathbf{W}_i^V). $$
Сначала для векторов запроса, ключей и значений делают линейное преобразование при помощи трёх матриц $\mathbf{W}^Q_i$, $\mathbf{W}^K_i$, $\mathbf{W}^V_i$. При этом для каждой ($i$-той) головы $\mathbf{h}_i$ набор матриц свой (свой "фокус внимания"). Если: $$ \mathbf{Q}:~(N,E),~~~~~~~\mathbf{K}:~(M,E_k),~~~~~~~\mathbf{V}:~(M,E_v),~~~~~~~~~~~~\mathbf{A}:~(N,E_a), $$ то, в общем случае, матрицы могут иметь следующие формы: $$ \mathbf{W}^Q_i:~(E,\,E_i),~~~~~~~~~~\mathbf{W}^K_i:~(E_k,\,E_i),~~~~~~~~~~\mathbf{W}^V_i:~(E_v,\,E_h),~~~~~~~~\mathbf{h}_i:~(N,\,E_h),~~~~~~~ \mathbf{W}^O:~(E_h\, H,~E_a). $$ После вычисления функции внимания Attn для каждой головы, получаются матрицы формы $(N,E_h)$. Их объединяют в одну (конкатенируют) по последнему индексу, что даёт матрицу $(N,~E_h\, H)$. Её свёртка с $\mathbf{W}^O$ приводит к финальной матрице $\mathbf{A}$ формы $(N,\,E_a)$.
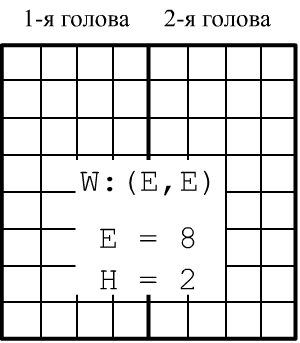В исходной статье (2017), где были
введены головы внимания, было положено $E_i=E_h=E/H$.
Это же соглашение принято в PyTorch
и матрицы всех голов упаковываются в одну c E колонками.
Для задачи само-внимания ($E_k=E_v=E$) такая матрица имеет квадратную форму $(E,E)$.
$$
\mathbf{W}^Q_i:~(E,\, E/H),~~~~~~~~\mathbf{W}^K:~(E_k,\,E/H),~~~~~~~~~~~~~\mathbf{W}^V_i:~(E_v,\,E/H),~~~~~~~~~~~~\mathbf{W}^O:~(E, ~E).
$$
При подобном выборе, чем больше голов, тем больше различных аспектов последовательности они могут
"разглядеть". Однако каждая голова при этом "видит хуже", т.к. оперирует эмбедингом размерности $E/H$.
🔥 Заметим, что в функции внимания в качестве параметров выступают элементы матрицы произведения $\mathbf{W}^Q\cdot\mathbf{W}^{K\top}:~(E,E_k)$, а не эти две матрицы по-отдельности. Однако, если $E_k=E$ и $E_i=E/H$, число элементов двух матриц равно $2\,E^2/H$, что при трёх и более головах меньше $E^2$ элементов их произведения.
MultiheadAttention в PyTorch
В PyTorch есть готовая функция многоголового внимания, оформленная как nn-слой:
✒ nn.MultiheadAttention
… (embed_dim, num_heads, dropout=0.0, bias=True, add_bias_kv=False,
… add_zero_attn=False, kdim=None, vdim=None)
Аргументы конструктора имеют следующие значения: embed_dim = E - размерность эмбединга; num_heads = H - число голов; $\text{kdim}=E_k$, $\text{vdim}=E_v$ - размерности ключей и значений (если они None, то полагаются равными E). Размерность эмбединга E должна быть кратна числу голов H. При задании параметров bias, add_bias_kv в True производится не только умножение запросов, ключей и значений на матрицы, но и сдвиг на вектор (общее линейное переобразование). Прямое распространение через модуль внимания имеет следующие параметры:
✒ nn.MultiheadAttention.forward
… (query, key, value, key_padding_mask=None, need_weights=True, attn_mask=None)
В простейшем случае на вход объекта MultiheadAttention подаются тензоры: $\mathbf{Q},~\mathbf{K},~\mathbf{V}$, а на выходе получается пара ($\mathbf{A}$, $\mathbf{W}$) - результат внимания $\mathbf{A}$ и тензор весов $\mathbf{W}$ (действие функции softmax для каждого примера батча):
- input: $~~\mathbf{Q}$: (N,B,E), $~~~\mathbf{K},\mathbf{V}$: (M,B,E)
- output: $\mathbf{A}$: (N,B,E), $~~~~~\mathbf{W}$ : (B,N,M),
Обратим внимание, что по аналогии с рекуррентными слоями индекс номера примера в батче B идёт не первым, а вторым (кроме результирующего тензора весов). Приведём пример использования многоголового внимания:
E, H, N, M, B = 100, 10, 3, 3, 1 Ek, Ev = 100, 100 Q, K, V = torch.rand(N, B, E), torch.rand(M, B, Ek), torch.rand(M, B, Ev) MHA = nn.MultiheadAttention(E, H, kdim=Ek, vdim=Ev) A,W = MHA(Q, K, V) print(tuple(A.shape), tuple(W.shape)) # (3, 1, 100) (1, 3, 3)
Размерности матриц равны: $\mathbf{W}^Q:$ (E, E), $\mathbf{W}^K:$ (E, kdim), $\mathbf{W}^V:$ (E, vdim), где размерности kdim,vdim или задаются, или равны E (они передаются в функцию linear, поэтому при умножении транспонируются). Размерность каждой головы равна E // H. Выходная матрица $\mathbf{W}^O:$ это слой Linear(E, E, bias=bias).
Если эмбединг входов одинаковый, то проекционные матрицы упакованы
в in_proj_weight формы (3*E,E),
иначе это три различных матрицы: q_proj_weight, k_proj_weight, v_proj_weight.
Смещение (если оно есть) это in_proj_bias формы (3*E,),
а выходной слой: out_proj:
for k, v in MHA.state_dict().items(): # in_proj_weight shape: (300, 100)
print(f'{k:20s} shape: {tuple(v.shape)} ') # in_proj_bias shape: (300,)
# out_proj.weight shape: (100, 100)
# out_proj.bias shape: (100,)
Маскированное внимание
Важными параметрами прямого распространения через слой многоголового внимания являются маски key_padding_mask и attn_mask.
Булева маска key_padding_mask: (B,M) позволяет исключать из механизма внимания некоторые пары ключей и значений (независимо для каждого примера батча B). Для этого номера исключаемых пар в маске необходимо пометить значением True.
Вещественная маска attn_mask: (N,M) прибавляется к весам внимания перед их нормировкой при помощи функции софтмакс. Обычно эта маска используется для точечного отключения конкретных весов. Для этого соответствующие элементы маски полагаются равными минус бесконечности, а остальные - нулю:
E, H, N, M, B = 8, 4, 3, 4, 1
Q, K, V = torch.rand(N,B,E), torch.rand(M,B,E), torch.rand(M,B,E)
MHA = nn.MultiheadAttention(E,H)
A,W = MHA(Q, K, V,
key_padding_mask=torch.tensor( [[False,True,False,True]]) )
print(W)
inf = float("-inf")
A,W = MHA(Q, K, V,
attn_mask=torch.tensor( [[inf, 0.0, 0.0, inf],
[0.0, 0.0, 0.0, 0.0],
[inf, 0.0, 0.0, inf]] ) )
print(W)
В первом случае key_padding_mask
отключила ключи с индексами 1 и 3
Ниже нулями забиты соответствующие им колонки матрицы весов W.
Маска attn_mask "удалила" угловые элементы матрицы весов внимания:
[[[0.5148, 0.0000, 0.4852, 0.0000], [[[0.0000, 0.4940, 0.5060, 0.0000], [0.5136, 0.0000, 0.4864, 0.0000], [0.2570, 0.2519, 0.2435, 0.2475], [0.5127, 0.0000, 0.4873, 0.0000]]] [0.0000, 0.4918, 0.5082, 0.0000]]],Из документа, посвящённого трансформеру, станет ясна практическая польза от применения этих масок.
Реализация MultiheadAttention
Воспроизведём вычисления, происходящие внутри слоя nn.MultiheadAttention. Нам потребуются следующие функции PyTorch:
from torch import bmm # пакетное умножение матриц from torch.nn.functional import linear as linear # линейная функция y = x@A^T + b from torch.nn.functional import softmax as softmax # функция софтмаксаВ функцию MultiHeadAttention, кроме матриц запросов Q, ключей K, значений V и масок key_mask, attn_mask, передадим также матрицы линейных преобразований, которые возьмём у слоя nn.MultiheadAttention. В комментариях, как обычно, приведены формы получающихся тензоров:
def MultiHeadAttention(Q,K,V, # Q:(N,B,E); K:(M,B,Ek); V:(M,B,Ev)
Wq, Wk, Wv, Wo, # матрицы поворта для Q,K,V,A
Bq=None, Bk=None, Bv=None, Bo=None, # матрицы смещения для Q,K,V,A
key_mask = None, # маска исключения ключей (B,M)
attn_mask = None): # аддитивная маска (N,M)
q = linear(Q, Wq, Bq) # (N,B,E) линейное преобразование
k = linear(K, Wk, Bk) # (M,B,E)
v = linear(V, Wv, Bv) # (M,B,E)
q = q.view(N, B*H, E//H).transpose(0,1) # (B*H, N, E/H) разбиваем на H голов
k = k.view(M, B*H, E//H).transpose(0,1) # (B*H, M, E/H)
v = v.view(M, B*H, E//H).transpose(0,1) # (B*H, M, E/H)
W = bmm(q, k.transpose(1,2))*float(E//H)**-0.5 # (B*H, N, M) размерность головы E/H
if attn_mask is not None: # аддитивная маска
W += attn_mask.unsqueeze(0) # (N,M) -> (1,N,M)
if key_mask is not None: # исключаем часть ключей
W = W.view(B, H, N, M)
key_mask = key_mask.unsqueeze(1).unsqueeze(2) # (B,1,1,M)
W = W.masked_fill(key_mask, float('-inf'))
W = W.view(B*H, N, M)
W = softmax(W, dim=-1) # (B*H, N, M)
A = bmm(W, v) # (B*H, N, E/H)
A = A.transpose(0, 1).contiguous().view(N,B,E) # (N, B, E)
W = W.view(B, H, N, M)
return linear(A, Wo, Bo), W.sum(dim=1) / H # (N, B, E), (B, N, M)
Сначала Q, K, V подвергаются линейному преобразованию linear. Затем они разрезаются на головы. Для этого меняется их форма и первые два индекса переставляются местами. В результате первый индекс нумерует и примеры, и головы. Использование далее метода умножения bmm производит перемножение прямоугольных матриц для каждого примера, каждой головы. Транспонирование и изменение формы тензора A в конце функции переводит его в исходную форму, подобную тензору Q.
В блоках if происзводится маскирование внимания. Сначала к весам W прибавляется маска attn_mask к которой добавляется одна размерность (и дальше включается механизм расширения). Затем булева маска key_mask служит для замены колонок для которых key_mask == True в минус бесконечность. После прохождения через функцию софтмакс, элементы матрицы весов в этих колонках будут равны нулю.
Если объект MHA создан при помощи конструктора nn.MultiheadAttention (как в предыдущем разделе), то вызов написанной функции, будет иметь следующий вид:
A2,W2 = MultiHeadAttention(Q,K,V,
MHA.in_proj_weight[0 : E] if Ek==E else MHA.q_proj_weight,
MHA.in_proj_weight[E : 2*E] if Ek==E else MHA.k_proj_weight,
MHA.in_proj_weight[E*2 : ] if Ek==E else MHA.v_proj_weight,
MHA.out_proj.weight,
MHA.in_proj_bias[0 : E],
MHA.in_proj_bias[E : E*2],
MHA.in_proj_bias[E*2:],
MHA.out_proj.bias,
attn_mask = attn_mask,
key_mask = key_mask )
print(((A1.detach() - A2.detach())**2).sum()**0.5) # сравниваем матрицы (округления)
print(((W1.detach() - W2.detach())**2).sum()**0.5)
Литература
Статьи
- 2014: Sutskever I, et al. "Sequence to Sequence Learning with Neural Networks"
- изобретение архитектуры Encoder-Decoder для RNN. - 2014: Bahdanau D., et al. "Neural Machine Translation by Jointly Learning to Align and Translate
- механизма Attention для Encoder-Decoder архитектуры. - 2017: Vaswani A., et al. "Attention is All You Need"
- отказ от рекуррентных сетей, архитектура Transformer (Google Brain)
Исходники
- The Annotated Encoder-Decoder with Attention
- NLP From Scratch: Translation with a Sequence to Sequence Network and Attention
- The Annotated Transformer - разбор кода трасформера.
- "Attention and Augmented Recurrent Neural Networks"
