ML: Интервальная вероятностная логика
Введение
При накоплении обыденных знаний в форме фактов и правил, человек редко использует бинарную логику.
Так как знания являются обобщением опыта, степень их истинности носит вероятностный и нечёткий характер.
Выводы из знаний, при помощи полученной информации, также делаются в условиях неопределённости.
В этом документе рассмотрен интервальный вероятностный подход к логике.
Предварительно имеет смысл ознакомится с основами вероятностных методов
и связью логики и вероятности.
Небесполезным будет также прочтение неформального введения в логику.
Непосредственным продолжением данной темы является
обсуждение нечёткой логики.
Несколько примеров
В реальном мире не бывает абсолютно истинных или ложных утверждений. Существует множество причин по которым следует отойти от бинарной (да-нет) логики при оценке истинности утверждений:
- будущие события всегда носят вероятностный характер;
- возможен недостаток информации о совершившемся событии;
- бывают уникальные, неповторяемые события;
- отношение к объекту или процессу часто оценочное или эмоциональное.
1. Вероятность. Утверждение "Монета, которую сейчас подбросят, упадёт гербом вверх" традиционно относят к теории вероятностей. Если монета честная (симметричная) и её бросают честно ("случайно"), то утверждение $A$ наделяется свойственной ему числовой характеристикой $P(A)=1/2$, называемой вероятностью события $A$. Практически это число измеримо, только при большом числе повторов, да и то в предположении постоянства "истинной" вероятности. Уход от "чистой" теории вероятностей начинается, если мы видим эту монету впервые и она находится в руках сомнительного субъекта.
2. Неопределённость.
"В комнате находится кот". Хотя кот уже находится (или не находится) в комнате,
это утверждение окажется истинным или ложным в будущем (в комнату необходимо зайти).
Если мы первый раз в этой комнате, то истинность утверждения не определена
(кот там может быть, а может его там и не быть).
Эту неопределённость важно отличать
от вероятности $P(A)=1/2$ в случае монеты, т.к. у нас нет причин считать нахождение кота
в комнате равновероятным событием. Естественно, если эта комната наша и у нас нет кота,
неопределённость снижается, хотя и не полностью (например, если уходя мы забыли закрыть окно).
3. Убеждённость.
"Графа, скорее всего убил дворецкий; у него был мотив и нет алиби".
Событие убийства уже произошло, причём, в отличии от монеты, оно принципиально неповторяемое.
Тем не менее, похожие прецеденты в прошлом (с другими преступлениями), позволяют высказывать некоторые
суждения.
Вначале, при полном отсутствии информации (никто не видел самого преступления), нельзя
дать однозначную оценку истинности утверждения.
По мере появления совокупности улик и мотивов, можно
предоставлять доводы за и против истинности этого утверждения, уменьшая его неопредлённость.
5. Оценка. "Этот кофе крепкий и горячий", "Маша красивая и сильная", "Старая машина едет быстро" - это всё оценочные суждения, связанные с нечёткими множествами ("чашки кофе разной температуры", "множество красивых женщин" и т.д.). В отличии от предыдущих примеров, в которых утверждение "на самом деле" или истинно или ложно, тут закон исключения третьего $A\vee \neg A ~=~ \mathbb{T}$ (истина) не работает. О таких оценочных утверждениях может быть известно всё, но тем не менее, их нельзя считать или истинными, или ложными. Оценочные суждения могут комбинироваться с вероятностными: "Завтра, скорее всего, пойдёт сильный дождь".
В этом документе мы будем опираться на относительно надёжный фундамент теории вероятностей, считая, что утверждение "на самом деле" или истинно, или ложно, но мы не обладаем всей полнотой информации. Вообще говоря, меры "уверенности" в истинности или степень "оценки" эмоционального суждения могут иметь математику, отличную от вероятностной. Тем не менее, по-возможности, вероятностная логика будет иметь дело с задачами, подобным первым четырём примерам. Пятому примеру посвящён следующий документ о нечёткой логике и теории множеств.
Вероятность истинности
Далее, если это не будет приводить к неоднозначности, вместо вероятности $P(A)$ события,
будем просто писать $A$, аналогично $A\,\&\,B$ вместо $P(A\,\&\,B)$ и т.д.
Кроме этого, будут использоваться два способа описания истинности утверждения $A$ о некотором событии или процессе.
Точечная мера $A$, как обычно, означает вероятность того
что событие произойдёт (или уже произошло).
Чем ближе $A$ к единице, тем "истиннее" утверждение.
Отрицание $\neg A$ или $\bar{A}$ утверждения $A$ имеет вероятность:
$$
\bar{A}=1-A.
$$
При этом предполагается выполнение тождеств теории вероятности
$A\vee B=A+B-(A\,\&\,B)$ и всех тождеств булевой алгебры:
$\neg(A\,\&\,B) = \bar{A}\vee \bar{B}$ и т.д., включая закон исключения третьего $(A\,\&\,\bar{A})=0$.
Интервальная оценка - это второй способ задания степени истинности утверждения $A$. Нижнюю границу интервала обозначим как $a$, а верхнюю - как $1-\bar{a}$: $$ A=[a,\,1-\bar{a}],~~~~~~~~~~a~\le~A ~\le~ 1-\bar{a},~~~~~~~~a+\bar{a}~\le~1, $$ где последнее неравенство означает, что верхняя граница не должна быть меньше нижней. Когда $a+\bar{a}=1$, вероятность события полностью определена. И наоборот, при $a=\bar{a}=0$, т.е. $A=[0,~1]$ - значение вероятности неопределено. Интервальная оценка позволяет отличать вероятностное, но определённое суждение $A=[0.5,\,0.5]$ (подбрасывание монеты) от неопределённого $A=[0,\,1]$ (кот в неизвестной комнате).
Учитывая, что всегда $\bar{A}=1-A$, для интервала вероятности истинности отрицания следует написать: $$ \bar{A}=[\bar{a},\,1-a]. $$ Интервалы высказывания и его отрицания могут не пересекаться ($a+\bar{a} \gt 0.5$) - более определённая ситуация, или не пересекаться (если $a+\bar{a} \le 0.5$) - менее определённая:
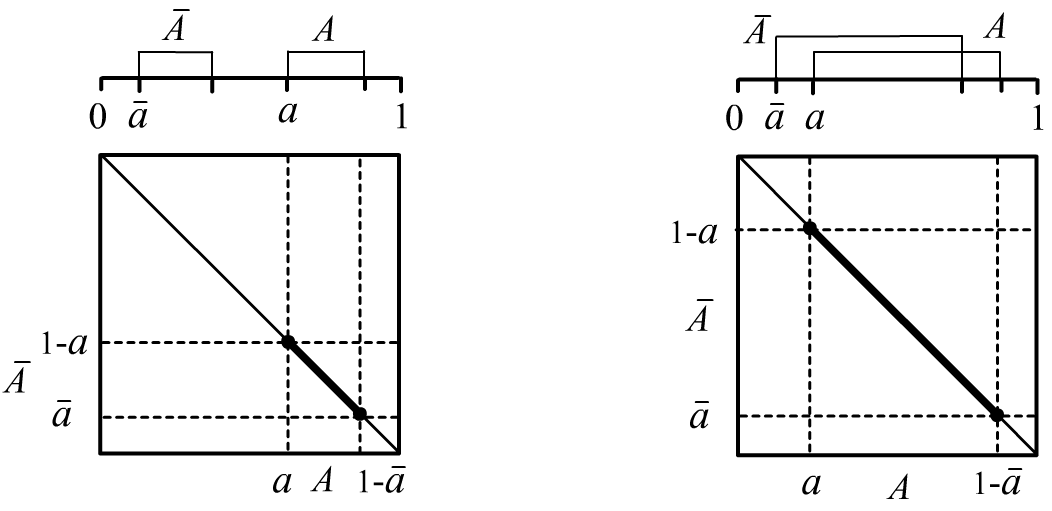
На плоскости $(A,\bar{A})$ возможные значения вероятностей утверждения и его отрицания находятся на отрезке, изображённом на рисунках жирной линией.
Детективная гипотеза "Графа убил дворецкий" в начале расследования имеет неопределённую истинность $[0,\,1]$. По мере расследования она может подкрепляться фактами за ($a$), так и опровергаться при появлении фактов против ($\bar{a}$). Естественно, даже при устранении неопределённости $(a+\bar{a}=1)$, получившееся число является лишь вероятностью истинности прошлого или будущего события. Если дворецкий убил графа с вероятностью $A=0.75$, это означает, что в четверти "параллельных вселенных" он не виновен. Стоит ли его осуждать в нашей вселенной?
Множество гипотез
При рассмотрении утверждения $A$ и его отрицания $\bar{A}$, мы видели, что их интервалы не могут быть произвольными и определяются двумя ($a$, $\bar{a}$), а не четырьмя параметрами. В общем случае, пусть есть множество $\mathbb{H}=\{H_1,...,H_n\}$ несовместных событий $H_i\,\&\,H_j = 0$ при $i\neq j$ (гипотез), которые производят разбиение пространства испытаний (в каждом испытании происходит ровно одно из $\mathbb{H}$). В этом случае: $$ H_1+...+H_n = 1,~~~~~~~~~~h_i \le H_i \le 1-\bar{h}_i,~~~~i=1...n $$ и условия непротиворечивости совокупности пар $(h_i,\,\bar{h}_i)$ для границ интервалов более сложное. Один из подходов к удовлетворению этим ограничениям был предложен в теории Демпстера-Шафера.
Опишем другой, более простой способ.
Зафиксируем значения нижних границы гипотез $\mathbf{h}=\{h_1,...,h_n\}$, так, чтобы их сумма не превышала единицы.
В векторных обозначениях такую сумму можно выразить при помощи вектора
с единичными компонентами $\mathbf{t}=\{1,...,1\}$ (это координаты вершины
$n$-мерного единичного куба, находящейся "напротив" начала координат):
$$
\mathbf{h}\,\mathbf{t} ~=~ \sum^n_{i=1} h_i ~\le~ 1.
$$
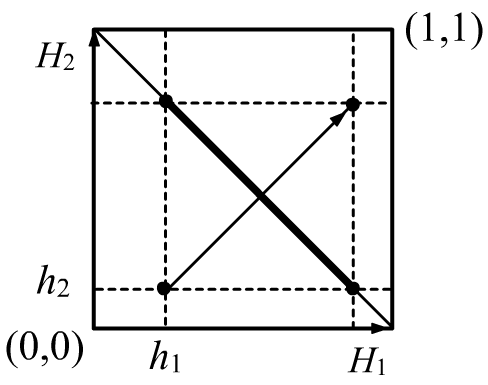
Вектор "настоящих" (но не известных) вероятностей $H_i$ гипотез удовлетворяет уравнению плоскости $\mathbf{H}\mathbf{t}=1$.
Так как $\mathbf{t}^2=n$, несложно видеть, что точка
$$
\mathbf{h}' = \mathbf{h} + \frac{1-\mathbf{h}\,\mathbf{t}}{n}\,\mathbf{t}
$$
также лежит в этой плоскости ($\mathbf{h}'\mathbf{t}=1$). Если сдвинутся на двойной вектор
$\mathbf{h}'-\mathbf{h}$ мы окажемся с противоположной стороны плоскости на таком-же расстоянии
(см. рисунок для $n=2$).
Эта точка и будет определять верхнюю границу интервалов истинности гипотез:
$$
H_i = [h_i,~h_i+\frac{2}{n}\,(1-\mathbf{h}\,\mathbf{t})].
$$
Рассмотрим в качестве примера $n=4$ гипотезы. Пусть $\mathbf{h}=\{0.0,~0.2,~0.2,~0.4\}$, тогда $\mathbf{h}\mathbf{t}=0.8$ и согласованные интервалы вероятностей истинности гипотез равны: $$ H_1=[0.0,\,0.1],~~~H_2=[0.2,\,0.3],~~~H_3=[0.2,\,0.3],~~~H_4=[0.4,\,0.5]. $$
Конъюнкция, дизъюнкция и импликация
Пусть заданы точечные значения вероятностей $A$ и $B$ двух событий
и больше о них ничего не известно.
Тогда интервалы для логического И (конъюнкции) и логического ИЛИ (дизъюнкции)
в теории вероятностей равны:
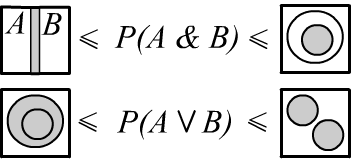$$
\begin{array}{lccclcccccc}
\max[0,~A+B-1]&\le& A\,\&\,B &\le& \min[A,\,B]\\[2mm]
\max[A,\,B]&\le& A\vee B &\le&\min[1,~A+B]
\end{array}
$$
Справа приведена графическая интерпретация этих неравенств. Например, максимальное значение пересечения событий (конъюнкции) будет когда одно является подмножеством другого. Если обе области событий без пересечения "помещаются" в пространстве испытаний, то минимальное значение конъюнкции равно нулю. Если же их объединение "не помещается", то их минимальное пересечение равно $P(A)+P(B)-1$.
В бинарной логике импликация $A\to B$ ложна для $\mathbb{T}\to \mathbb{F}$ (из истины нельзя получить ложь) и истинна в остальных случаях. Кроме этого, она выражается через дизъюнкцию и отрицание: $A\to B~~\equiv~~\bar{A} \vee B.$
| $W$ | $\bar{W}$ | Tot | |
|---|---|---|---|
| $B$ | 8 | 2 | 10 |
| $\bar{B}$ | 32 | 58 | 90 |
| Tot | 40 | 60 | 100 |
Из определения $P(A\to B)=P(A,B)/P(A)$, при известных точечных вероятностях $A$, $B$ (и в отсутствии другой информации), имеем $$ \max\bigr[0,~1-\frac{1-B}{A}\bigr]~~~~~~~\le~~~~A\to B~~~~\le~~~~~~\min\bigr[1,~B/A\bigr]. $$ Верхняя граница этого интервала совпадает с определением импликации Гогена в многозначной логике.
Интервальные соотношения
Если известны только интервальные вероятности $A=[a,~1-\bar{a}]$, $B=[b,~1-\bar{b}]$ и другой информации нет, то интервалы для конъюнкции и дизъюнкции имеют вид: $$ \begin{array}{lclclcccccc} A\,\&\,B &=& \bigr[ \max(0,~a+b-1) &,& 1-\max(\bar{a},\,\bar{b})\bigr]\\[2mm] A\vee B &=& \bigr[ \max(a,b) &,& 1-\max(0,~\bar{a}+\bar{b}-1)\bigr]\\[2mm] \end{array} $$
Для нижней границы интервала импликации $P(A\to B)=P(A\,\&\,B)/P(B)$ необходимо взять минимальную конъюнкцию $A\,\&\,B$ и максимальную вероятность $A$. Для верхней границы - наоборот (но не превышающую $1$): $$ \begin{array}{lclclcccccc} A\to B &=& \Bigr[ \max\Bigr(0,~\displaystyle\frac{a+b-1}{1-\bar{a}}\Bigr),~~~ 1- \max\Bigr(0,~ 1+\frac{\max(\bar{a},\,\bar{b})-1}{a}\Bigr)\Bigr]. \end{array} $$
Интервалы для конъюнкции и дизъюнкции несложно получить из соотношений предыдущего раздела. Возможны также следующие полезные рассуждения.
Представим, что существует большое количество равновероятных элементарных событий $\mathbb{E}=\{E_1,...,E_n\}$.
Любое событие $A$ является объединением некоторой части элементарных событий (подмножество множества $\mathbb{E}$).
Запишем это в виде последовательности $A=(01110?1??011)$ длины $n$, где наличие $1$ на $i$-том месте означает,
что $E_i\in A$, а $0$ - что $E_i\not\in A$. Вопросительные знак помечает факт
неопределённой принадлежности (неизвестно $E_i\in A$ или $E_i\not\in A$).
Число известных единиц равно $a\cdot n$, а число известных нулей $\bar{a}\cdot n$,
поэтому $A = [a,~1-\bar{a}]$.
Если вопросов нет, то это точечная, однозначная вероятность $a+\bar{a}=1$ (монета). Если же вся последовательность
состоит из вопросов, то вероятность $A=[0,\,1]$ полностью неопределена (кот в комнате).
Пусть для событий известны только $(\bar{a},a)$, $(\bar{b},b)$, а порядок символов $0,1,?$ в последовательностях неизвестен. Минимальное значение их конъюнкции будет, когда все $?=0$ (ровно $a\cdot n$ единиц) и единицы обоих последовательностей максимально не пересекаются. Максимальное значение конъюнкции получается когда $?=1$ (ровно $\bar{a}\cdot n$ нулей) и последовательно максимально пересекаются на единицах: $$ \min(A\,\&\,B) = \begin{array}{lclll} ~\overbrace{1...111}^{a}\,\overbrace{0...0}^{1-a}\\ ~\underbrace{0...0}_{1-b}\,\underbrace{1...111}_{b} \end{array} =\max(0,~a+b-1), ~~~~~~~~~~~~ \max(A\,\&\,B) = \begin{array}{lclll} ~\overbrace{1...11}^{1-\bar{a}}\,\overbrace{0...0}^{\bar{a}}\\ ~\underbrace{1...111}_{1-\bar{b}}\,\underbrace{0...0}_{\bar{b}} \end{array} =\min(1-\bar{a},\,1-\bar{b}). $$
Естественно, любая значимая информация уменьшает степень неопределённости. Например, если известно, что события независимы $P(A,B)=P(A)\,P(B)$, то $$ A\Prep B:~~~~~~~A\,\&\,B = [a\cdot b,~~~(1-\bar{a})\cdot(1-\bar{b})]. $$
В априрном предположении равновероятности положения символов $0,1,?$ в последовательности, можно получить вероятность распределения "истинного значения" $P(A)$ в интервале $A=[a,~1-\bar{a}]$.
Логический вывод
В бинарной логике из $P$ логически следует $Q$,
если всегда, когда формула $P$ истинна, то истинна и формула $Q$.
Это обозначается так: $P\Rightarrow Q$.
Логический вывод - это способ получения одних истинных формул из других, также истинных.
Не стоит путать вывод и импликацию $P\to Q$, которая является логической связкой,
принимающей значения $0$ или $1$.
Вывод modus ponens: $A,~A\to B ~~\Rightarrow~~ B$ в булевой логике означает, что, если истинно утверждение $A$ и из $A$ следует $B$ (импликация), то можно считать истинным (и выводимым) утверждение $B$.
В интервальной вероятностной логике, кроме указания правила вывода, необходимо также знать интервал истинности для выводимой формулы. Пусть известно, что $A~=~[a,~1-\bar{a}]$ и $A\to B~=~[r,~1-\bar{r}]$ Используя тождество полной вероятности, можно написать: $$ P(A)\cdot P(A\to B) = P(A,B) ~~~~\le~~~ P(B)~~~~ \le~~~ 1. $$ С другой стороны $\min\bigr(A\cdot (A\to B)\bigr) ~=~ a\cdot r$, поэтому modus ponens выглядит следующим образом: $$ A~=~[a,~1-\bar{a}],~~~A\to B~=~[r,~1-\bar{r}]~~~~~~~~~~~\Rightarrow~~~~~~~~~~B~=~[a\cdot r,~1]. $$
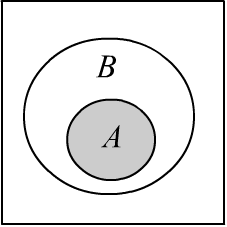Если $r=1$, то $B=[a,~1]$. Графически это очевидный результат. Если всегда, когда происходит событие $A$, также происходит и событие $B$,
т.е. условная вероятность
$P(A\to B)=1$. Это означает, что событие $A$ является подмножеством события $B$.
В пространстве испытаний
минимально возможная площадь $B$ не меньше площади $A$ (рисунок справа).
1) Если связь между этими двумя событиями неизвестна, для вычисления их конъюнкции необходимо пользоваться общей формулой: $$ R\,\&\,F ~=~ [0.6+0.9-1,~~~1-\max(0.2,0.1)]~=~[0.5,~0.8],~~~~~~\Rightarrow~~~~~~W=[0.5,~1]. $$ 2) Если же известно, что события дождя и забывания зонта независимы, оценка для интервала вероятности $B$ получается чуть более узкой: $$ R\,\&\,F~=~R\cdot F ~~=~~ [0.6\cdot 0.9,~0.8\cdot 0.9] ~~~=~~~ [0.54,~0.72]~~~~~~~\Rightarrow~~~~~~~W=[0.54,~1]. $$
Пример: Шкатулка и сундук
Рассмотрим мир прямоугольных закрытых ящиков со всегда истинной аксиомой
Примеры выводов
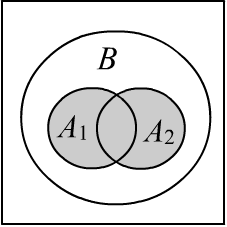Пусть есть два истинных правила
$$
A_1\to B,~~~~~ A_2\to B
$$
и вероятностные точечные посылки $P(A_1),~P(A_2)$. Тогда (см. рисунок):
$$
\left\{
\begin{array}{lll}
A_1\to B\\
A_2\to B\\
\end{array}
\right.
~~~~~~~~~~~\Rightarrow~~~~~~~~~~P(A_1\vee A_2)~\le~ P(B)~\le~ 1.
$$
В случае, если посылки независимы, то $B = [a_1+a_2-a_1a_2,~~1].$
Рассмотрим два истинных правила $$ A_1\,\&\,\bar{A}_2\to B,~~~~~~~ A_2\,\&\,\bar{A}_1\to \bar{B}. $$ В булевой логике посылки не могут быть одновременно истинными, иначе будет получено противоречие: $B,\,\bar{B}$. Это учтено в конъюнкциях посылок. В данном случае имеем: $$ b = \min B = \min(A_1\,\&\,\bar{A}_2),~~~~~~~~ \bar{b}~=~\min \bar{B} = \min(\bar{A}_1\,\&\,A_2). $$ Если утверждения $A_1, A_2$ независимы, то для $B$ имеем интервальную оценку: $[a_1\,(1-a_2),~1-(1-a_1)\,a_2]$, т.е. отличны от нуля обе границы интервала.
Если известно, что $A\to B$ и истинным является $B$, то в классической логике вывести $A$, вообще говоря, нельзя. Тем не менее, информация о $B$ должна как-то повлиять на наши выводы. В вероятностной логике это соответствует апостериорному изменению вероятности утверждении $A$ по формуле Байеса: $$ P(B\to A) = P(A\to B)\,P(A)/P(B). $$
