ML: Байесовские методы

Введение

В задачах машинного обучения и алгоритмах искусственного интеллекта важную роль играет формула Байеса. Документ является продолжением введения в теорию вероятностей и посвящён различным аспектам применения этой формулы.

Формула Байеса

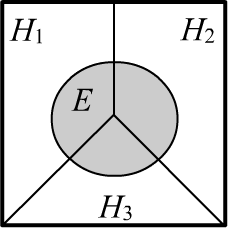
Пусть есть $n$ несовместных (непересекающихся) событий $\{H_1,...,H_n\}$, $H_i\,\cap\,H_j=\varnothing$, которые далее будут называться гипотезами. Предполагается, что одна из них истинна (обязательно происходит в испытании): $$ \sum_i P(H_i) = 1. $$ В простейшем случае может быть две несовместные гипотезы, которые состоят в том, что некоторое утверждение $D$ либо истинно, либо ложно:

$H_1: $ "человек болен болезнью $D$,    $H_2: $ "человек не болен болезнью $D$".

Будем считать, что известны вероятности гипотез $P(H_i)$. Их можно получить из наблюдений (выше - это доля больных в популяции - objectivist interpretation) или это может быть степень "убеждённости" или "веры" в истинность гипотезы тем, кто принимает некоторое решение (subjectivist interpretation). Эти вероятности называют априорными ("до опытные", лат. "a priori").

Когда наступает некоторое событие $E$ (несущее новую информацию), оно может изменить вероятности гипотез на апостериорные вероятности $P(E\to H_i)$ (полученные из опыта, лат. "a posteriori"). Они определяются формулой Байеса: $$ P(E\to H_i) ~=~ \frac{P(E,H_i)}{P(E)} ~=~ \frac{P(H_i)\,P(H_i\to E)}{P(E)}. $$ Вероятность события $P(E)$ для полных (покрывающих все случаи) и несовместных гипотез вычисляется по формуле полной вероятности: $$ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~P(E) ~=~ \sum_j P(H_j)\,P(H_j\to E) ~=~ \sum_j P(E,\,H_j). $$ В результате сумма $P(E\to H_i)$ по всем $H_i$ равна единице (истинна одна из гипотез).

По формуле Байеса апостериорная вероятность $P(E\to H_i)$ пропорциональна априорной вероятность $P(H_i)$, умноженной на "функцию правдоподобия" (likelihood) $P(H_i\to E)$ события $E$ для гипотезы $H_i$. В частности, если вероятность события не зависит от истинности гипотезы $P(H_i\to E)=P(E)$, то априорная вероятность не изменяется: $P(E\to H_i)=P(H_i)$.

Часто накопить статистику для вычисления вероятностей $P(H_i\to E)$ проще, чем для $P(E\to H_i)$. Например, в случае $H:$ "человек болен данной болезнью", можно взять группу больных и вычислить по ней вероятность $P(H\to E)$ для симптома $E$. В то-же время симптом $E$ может возникать по множеству самых разнообразных причин (болезней), отличных от болезни $H$.

Кроме этого вероятности $P(H\to E)$ часто стабильнее, чем с $P(E\to H)$. Например, пусть началась эпидемия. Тогда вероятность $P(H)$ вырастает, а $P(H\to E)$ останутся неизменными. По формуле Байеса $P(E\to H)$, конечно, также увеличится.

Пример: Тестирование болезни

$p$ ${n}$ Tot
$d$ 9 1 10
$\bar{d}$ 90 9900 9990
Tot 99 9901 10000
Пусть у человека провели тестирование по выявлению некоторой болезни $D$. Известно, что этот тест в $90\%$ случаев даёт позитивный результат если человек действительно болен. Если же человек здоров, тест ошибочно выдаёт позитивный результат в 0.9% случаев. Пусть также известно, что на 10'000 человек этой болезнью болеет 10 человек.

Будем вместо событий говорить о случайных величинах, принимающих два значения
Гипотеза $H=\{d,\bar{d}\}$, где $d$ - "человек болен болезнью $D$" и $\bar{d}$ - "человек не болен этой болезнью";
Событие $~E=\{p,n\}$, где $p$ - тест положителен, $n$ - тест отрицателен: $$ P(d\to p) = 0.9,~~~~~~~P(\bar{d}\to p) = 0.009,~~~~~~P(d) = 0.001. $$ Справа в таблице приведена статистика (в людях) на основании которой получены оценки для этих вероятностей. Значения $P(H\to E)$ вычисляются по строкам, а $P(E\to H)$ - по столбцам: $P(d\to p)=9/10$, $P(p \to \bar{d})=90/99$.

Вероятность обнаружить позитивный тест (независимо от состояния человека) равна: $$ P(p ) = P(d)\,P(d\to p ) ~+~ P(\bar{d})\,P(\bar{d}\to p ) = 0.9*0.001 + 0.009*(1-0.001)= 0.0099 $$ Естественно это же значение можно получить и из таблицы (tot в первой колонке 99/10000).

По формуле Байеса апостериорная вероятность оказаться больным равна: $$ P(p \to d) = \frac{P(d)\,P(d\to p )}{P( p )} = \frac{0.001\cdot 0.9}{0.00989} = 0.091. $$ Из таблицы этот результат получается по первой колонке: 9/99.

Любопытно, что, хотя тест достаточно точно работает на здоровых людях (ошибается $9$ раз на $1000$ тестов), вероятность оказаться больным при однократном положительном тесте равна всего $9\%$. Этот, на первый взгляд, странный результат связан с тем что, хотя ошибок у теста мало, доля больных среди всей популяции ещё меньше. Стоит проанализировать таблицу приведенную выше (если тест провести у всей популяции позитивный результат будет у 99 человек, хотя среди них только 9 больных).

☝ Обычно удобнее нормировать апостериорные вероятности гипотез в конце, опуская при вычислениях одинаковые множители, которые от гипотез не зависят. Для примера с тестами это будет выглядеть так (знак $\sim$ означает, что величины пропорциональны, т.е. равны с точностью до общего множителя, независящего от $d$, $\bar{d}$): $$ \begin{array}{lclcl} P( p \to d) &\sim& P(d) \, P(d\to p ) &=& 0.9\cdot 0.001, \\ P( p \to \bar{d}) &\sim& P(\bar{d})\, P(\bar{d}\to p ) &=& 0.009\cdot 0.999. \end{array} $$ Запишем $P( p \to H)$ как вектор, компоненты которого соответствуют $H=d$ и $H=\bar{d}$: $$ P( p \to H) ~\sim~ \bigr\{ 0.9\cdot 0.001,~~~~ 0.009\cdot 0.999\bigr\} ~\sim~ \bigr\{ 0.1,~~~~ 0.999\bigr\}, $$ где из компонент снова вынесены и опущены общие множители. Теперь вектор необходимо отнормировать на единицу: $P( p \to H)=\bigr\{ 0.1,~~~~ 0.999\bigr\}/(0.1+0.999)=\bigr\{ 0.091,~~~~ 0.909\bigr\} $.

Последовательность наблюдений

При принятии решений, формулу Байеса используют для пересчёта вероятностей по мере поступления новой информации. Пусть было проведено два независимых теста (последовательно или одновременно, но в различных лабораториях). Какими станут апостериорные вероятности в этом случае?

Обозначим через $E_1$, $E_2$ - два условно независимых события (например "pp" или "pn"). Вероятность истинности гипотезы $H_i$, после возникновения событий, по формуле Байеса равна (считаем $\{E_1,\,E_2\}$ одним событием): $$ P(E_1,E_2 \to H_i) = \frac{P(H_i)\,P( H_i\to E_1,E_2 )}{P(E_1,E_2)} = \frac{P(H_i)\,P(H_i\to E_1)\,P(H_i\to E_2)}{P(E_1,E_2)}. $$ Во втором равенстве учтено, что события $E_1$ и $E_2$ условно (при гипотезе $H_i$) независимы. Вероятность в знаменателе, как и раньше, находится из условия нормировки $P(E_1,E_2 \to H_i)$: $$ P(E_1,E_2) ~=~ \sum_j P(H_j)\,P(H_j\to E_1)\,P(H_j\to E_2). $$

Обратим внимание, что, хотя проведенные тесты условно независимы, но при этом не безусловно независимы: $P(E_1,E_2) \neq P(E_1)\,P(E_2)$, Почему так происходит?

Ответ Проще понять это на примере тестирования болезни. Соотношение $P(E_1,E_2) = P(E_1)\,P(E_2)$ было бы верным, если бы результаты тестов $E_1$, $E_2$ были бы получены у двух случайно выбранных людей. В нашем случае тест проводится с одним и тем же человеком который или болен или здоров. Мы не знаем какая гипотеза верна, но в любом случае выполняется одна из них. Поэтому $P(E_1,E_2) ~=~ P(h)\,P( h\to E_1,E_2)+P(\bar{h})\,P(\bar{h}\to E_1,E_2 )$.

Формулу для апостериорной вероятности можно переписать следующим образом: $$ P(E_1\to H_i) = \frac{P(H_i)\,P(H_i\to E_1 )}{P(E_1)},~~~~~~~~~~~~~~ P(E_1,E_2 \to H_i) = \frac{P(E_1\to H_i)\,P(H_i \to E_2)}{P(E_1\to E_2)}. $$ Таким образом, событие $E_1$ превращает априорную вероятность $P(H_1)$ в $P(E\to H_1)$, после чего она (при помощи той-же формулы Байеса) превращается в ещё более уточнённую вероятность гипотезы $P(E_1,E_2\to H_i)$ и т.д. При этом последовательность условно независимых событий не играет роли.

Пример вычислений на numpy

Приведём пример вычислений с тестированием болезни на Python при помощи библиотеки NumPy: 
import numpy as np
np.set_printoptions(precision=5, suppress=True)
Совместные вероятности будем начинать с префикса P_, а условные с C_.
Нумерация событий: E=[p,n] и гипотез: H=[б,з]. Исходные данные имеют вид: 

NH, NE = 2, 2                          # число гипотез и событий

P_H  = np.array([0.001, 1-0.001])      # [P(б), P(з)]

C_EH = np.array([[  0.9,   0.009],     # P(б -> p) P(з -> p)
                 [1-0.9, 1-0.009] ])   # P(б -> n) P(з -> n)
Результаты однократного теста: 
C_HE = ( C_EH*P_H.reshape(1,NH) ).T    # [[P(p -> б), P(n -> б)],      [[0.09099 0.0001]
C_HE /= C_HE.sum(0)                    #  [P(p -> з), P(n -> з)]]   =   [0.90901 0.9999]]
Результаты двух тестов: 
C_HEE = (C_EH.reshape(NE,1,NH)*C_EH.reshape(1,NE,NH)*P_H.reshape(1,1,NH)).transpose(2,0,1)
C_HEE /= C_HEE.sum(0)

# P(pp -> б)  P(pn -> б)  [[[0.90917 0.01   ]
# P(np -> б)  P(nn -> б)    [0.01    0.00001]]
#
# P(pp -> з)  P(pn -> з)   [[0.09083 0.99   ]
# P(np -> з)  P(nn -> з)    [0.99    0.99999]]]

Таким образом, вероятность оказаться больным при двух положительных тестах $P(pp\to \text{б})=0.909$ существенно выше, чем при одном: $P(p\to \text{б})=0.091$.

Задача классификации

В задаче классификации с непересекающимися классами, объект с признаками $\mathbf{x}=\{x_1,...,x_n\}$ необходимо отнести к одному из $C$ классов. Пусть $P(\mathbf{x} \to c)$ - условная вероятность того, что объект с признаками $\mathbf{x}$ принадлежит $c$-тому классу: $c\in [0...C-1]$. Тогда формулу Байеса можно записать следующим образом: $$ P(\mathbf{x} \to c) ~=~ \frac{p(c,\mathbf{x})}{p(\mathbf{x})} = \frac{P(c)\,p(c\to \mathbf{x})}{p(\mathbf{x})}, ~~~~~~~~~~~~~ p(\mathbf{x}) ~=~ \sum_\alpha P(\alpha)\,p(\alpha\to \mathbf{x}), $$ где $P(c)$ - вероятности принадлежности случайно выбранного объекта к классу $c$ (независимо от значений его признаков), а $p(c\to \mathbf{x}) = p(c,\mathbf{x})/P(c)$ - распределение плотности вероятностей значений признаков $\mathbf{x}$ для объектов из данного класса $c$. Нормировка в знаменателе $p(\mathbf{x})$ - это распределение объектов в пространстве признаков. Если есть $N$ объектов, то $p(\mathbf{x})\cdot N$ - это плотность числа объектов единице объёма.

Таким образом, чтобы получить вероятность $P(\mathbf{x}\to c)$, необходимо знать вероятности классов $P(c)$ и плотность распределения $p(c\to \mathbf{x})$. Если обучающая выборка не смещена (классы в ней представлены с такой же частотой, что и в тестовой), то $P(c)$ получить несложно. А вот значения $p(c\to \mathbf{x})$ в многомерном пространстве признаков часто найти непросто. Если объекты класса образуют компактные "кластеры", то $p(c\to \mathbf{x})$ можно аппроксимировать гладкими функциями (например, многомерными распределениями Гаусса). Параметры этих функций получают по множеству обучающих примеров. Другой подход - это поиск ближайших соседей к точке $\mathbf{x}$ в каждом классе и построение по ним аппроксимирующих поверхностей $p(c\to \mathbf{x})$.

Иногда неплохие результаты даёт наивный Байес, в котором предполагается условная независимость признаков: $$ p(c\to \mathbf{x}) ~=~p(c\to x_1)\cdot...\cdot p(c\to x_n). $$ Вероятности $p(c\to x_i)$ особенно легко вычисляются для категориальных или бинарных признаков. В этом случае такой классификатор может оказаться эффективнее метрических моделей. Если признаки непрерывные, то для $p(c\to x_i)$ по обучающим данным можно строить гистограммы или вычислять статистики (например, когда считается, что $p(c\to x_i)$ имеет нормальное распределение).

При использовании наивного Байеса могут возникать две проблемы - потеря точности при перемножении небольших чисел и равенство нулю некоторых вероятностей $p(c\to x_i)$ (если обучающих данных мало).
Первая проблема решается переходом к логарифмам (вместо произведения будет сумма). Для борьбы с нулевыми вероятностями применяют сглаживание Лапласа.

Определение частей речи

Байесовскую формулу можно использовать для присваивания каждому слову $w_i$ предложения его части речи $t_i$: существительное (N), прилагательное (A), глагол (V) и т.д. (Part-of-Speech Tagging). Пусть $t_i$ - один из маркеров (N, A, V...). Если для текста слов $w_1...w_n$ известна условная вероятность $P(w_1,...,w_n\to t_1,...,t_n)$, то задача решается поиском макимума этой вероятности: $$ t_1,...,t_n = \arg\max_{t_1,...,t_n}\,P(w_1...w_n\to t_1...t_n). $$ Для оценки вероятности запишем формулу Байеса: $$ P(w_1...w_n\to t_1...t_n) ~=~ \frac{P(w_1...w_n,t_1...t_n)}{P(w_1...w_n)} ~=~ \frac{P(t_1...t_n)\,P( t_1...t_n \to w_1...w_n)}{P(w_1...w_n)} $$ Для максимизции по $t_i$ достаточно найти только числитель. Вероятность $P(t_1...t_n)$ характеризует степень правдоподобности данной последовательности частей речи (например N V более вероятно, чем A V). В первом приближении для её оценки, можно использовать биграммы. Для этого в цепном правиле делается марковское упрощение: $P(t_1...t_{k-1}\to t_k)=P(t_{k-1}\to t_k)$: $$ P( t_1...t_n) = P(t_1)\cdot P(t_1\to t_2)\cdot... \cdot P(t_{n-1}\to t_n). $$ Вторая вероятность в простейшем случае оценивается при помощи таких биграмм: $$ P( t_1...t_n \to w_1...w_n) ~=~ P( t_1...t_n \to w_1)\cdot ... \cdot P( t_1...t_n \to w_1) ~=~ P(t_1\to w_1)\cdot...\cdot P(t_n\to w_n). $$ При этом делается предположение (достаточно грубое) о условной независимости слов в последовательности. Заметим, что по той же теореме Байеса $P(t\to w)=P(w\to t)\,P(w)/P(t)$.

Угадать задуманное

Достаточно распространены интеллектуальные системы, задача которых состоит выяснении намерений человека. Для этого система задаёт последовательность вопросов, на которые человек отвечает Да или Нет. Известным примером является игра Akinator которая угадывает задуманный человеком персонаж.

Предположим, человек задумал один из объектов $X=\{x_1,...,x_N\}$. Система задаёт вопрос $Q_i\Rightarrow \{y_i, n_i\}$, на который получает бинарный ответ $y_i$ (yes=да) или $n_i$ (no=нет). Например: "Ваш персонаж женщина?", "Ваш персонаж из реальной жизни?", "Ваш персонаж дружит с медведем?" и т.д. При построении подобной системы необходимо учитывать, что человек, отвечая может намеренно или случайно давать неверные ответы. Поэтому в общем случае от нуля отличны обе условные вероятности: $P(X\to y_i)$ и $P(X\to n_i)$ - получить на вопрос $Q_i$ ответ $y_i$ или $n_i$, если задуман объект из множества $X$.

yes $y_1$ $y_2$ ... $y_M$ $P(x)$
$x_1$ 9 1 ... 2 0.001
$x_2$ 10 0 ... 25 0.008
... ... ... ... ... ...
$x_N$ 0 890 ... 100 0.02
Пусть есть фиксированный набор $N$ объектов и $M$ вопросов. В процессе работы система должна обучаться, запоминая ответы людей. В результате возникает таблица подобная приведенной справа (число ответов $y_j$ на вопрос $Q_j$, когда задуман объект $x_i$) и аналогичная таблица для ответов "no". На основании этих данных для пар $(x_i,y_j)$ и $(x_i,n_j)$ можно получить вероятности $P(X\to Q)$ - по строкам таблиц и $P(Q\to X)$ - по их столбцам. Кроме этого, таблицы дают вероятности $P(X)$ задумываемых людьми персонажей.

Обозначим чере $I_k$ последовательность $k$ вопросов-ответов, полученных системой: $I_k=\{Q_1,...,Q_k\}$.
На основании этой информации формируются условные вероятности $P(I_k\to X)$ для каждого объекта из $X$.
При помощи формулы Байеса можно записать: $$ P(I_k\to X) = \frac{P(X)\,P(X\to I_k)}{P(I_k)} = \frac{P(X)\,P(X\to Q_1)...P(X\to Q_k)}{P(I_k)}, $$ где во втором равенстве сделано предположение (сравнительно грубое) о "не влиянии" пар вопросов-ответов друг на друга. Нормировочная вероятность $P(I_k)$, как обычно, находится из условия нормировки (сумма по всем $x_i$), в предположении, что человек задумал известный системе объект. Так как задача состоит в поиске $x$ с максимальным значением $P(I_k\to X)$, знаменатель можно опустить: $$ x= \text{arg}\max_X ~\,P(X)\,P(X\to Q_1)...P(X\to Q_k). $$

Выбор очередного вопроса $Q$ после серии вопросов-ответов $I_{k-1}$ производится аналогично алгоритму ID3 построения деревьев решений . Единственное отличие состоит в том, что "признак" $Q$ может иметь два значения $\{y,n\}$. Оптимальным является вопрос, который делает распределение вероятностей $P=P(I_{k-1},\, Q_k\to X)$ максимально неравномерным (повышает вероятности отдельных объектов). Энтропия $H[P]$ такого распределения должна быть минимальной (усредняем энтропии для "да" и "нет" ответов): $$ Q = \text{arg}\min_{Q}~ H[ P(I_{k-1},\, y\to X)]\,P(y) + H[ P(I_{k-1},\, n\to X)]\,P(n), $$ где вероятности $P(Q)$ находятся с учётом известной к этому моменту вероятности объекта $x$: $$ P(Q) = \sum_{x} P(X\to Q)\,P(I_{k-1}\to X). $$

Оценка параметров модели

Часто необходимо оценить некоторый, например, непрерывный параметр $\theta$ по имеющемуся наблюдению $x$. Обычно $\theta$ является параметром статистики (вероятность события, параметры распределения и т.п.).

Пусть известно априорное распределение вероятностей $p(\theta)$ параметра $\theta$. При полном отсутствии информации о его значении, распределение является равномерным $p(\theta)=\text{const}$. Если были предыдущие наблюдения или существуют некоторые субъективные соображения, функция распределения $p(\theta)$ может быть более определённой.

Апостериорное распределение параметра (после наблюдения $x$) вычисляется, как обычно, по формуле Байеса: $$ p(x\to \theta) ~=~ \frac{p(\theta)\,p(\theta\to x)}{p(x)},~~~~~~~~~~~~~~~p(x) ~=~ \int p(\theta)\,p(\theta\to x)\,d\theta, $$ где интегрирование ведётся по всей области "разрешённых" значений $\theta$. Для вычисления $p(x\to \theta)$, кроме априорного распределения $p(\theta)$, необходимо знать функцию правдоподобия $p(\theta\to x)$. Чаще всего она задаётся из теоретических соображений.

Когда параметр $\theta$ является многомерной векторной величиной $\{\theta_1,...,\theta_n\}$, вычисление $n$-мерного интеграла с требуемой точностью может быть затруднительным. Для избежания подобных трудностей, выбирают такую $p(\theta)$, чтобы интеграл не только вычислялся аналитически, но и, полученное распределение $p(x\to \theta)$, при дальнейших наблюдениях также приводило к аналитическим результатам.

◊ Рассмотрим в качестве примера определение вероятности события по наблюдению факта его наступления.
В этом случае $x=1$ (событие в наблюдении наступило) и $x=0$ (не наступило). Выберем в качестве априорного распределения закон Бернули: $$ p(\theta) = \frac{\theta^{\alpha-1}\,(1-\theta)^{\beta-1}}{\mathrm{B}(\alpha,\beta)}. $$ Вещественные величины $\alpha,\beta$ являются гиперпараметрами, задание которых приводит к различным формам распределения $p(\theta)$. Например $\alpha=\beta=1$ - это равномерное распределение. При $\alpha=\beta=10$ - распределение имеет симметричный максимум в окрестности $\theta=0.5$ и т.д. Нормировочный множитель $\mathrm{B}(\alpha,\beta)$ является бета-функцией, выражающуюся через гамма-фукции: $$ \mathrm{B}(\alpha,\beta) = \int\limits_0^1 t^{\alpha-1}(1 - t)^{\beta-1}\,dt = \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha+\beta)}. $$

Если событие случайно и обладает стабильной частотой, то вероятность того, что оно произойдёт или не произойдёт равно: $$ p(\theta\to x) = \left\{ \begin{array}{lll} \theta & x=1\\ 1-\theta & x=0 \end{array} \right. $$

В общем случае, после $n+m$ наблюдений, в которых событие произошло $n$ раз и $m$ раз не произошло, апостериорная вероятность будет равна: $$ P(n,m\to \theta) = \frac{x^{n+\alpha-1}\,(1-x)^{m+\beta-1}}{\text{B}(n+\alpha,\,m+\beta)}. $$ В зависимости от значения гиперпараметров $\alpha,\beta$ и результатов наблюдений, получается то или иное распределение для значения вероятности $\theta$.