ML: Вывод в вероятностных моделях

Введение

Даже если $n$ случайных величин бинарны, для задания их совместной вероятности требуется $2^n-1$ чисел, что при больших $n$ становится проблематично в вычислительном отношении и невозможно в практическом. Сети доверия или байесовские сети - это графические модели, которые позволяют провести декомпозицию (упрощение) совместной вероятности большого числа случайных величин.

Этот документ продолжает обсуждение теории вероятностей, комбинаторных и байесовских методов. Полезно также предварительно ознакомиться с введением в логику и связью логики и вероятности.

Байесовская сеть

Рассмотрим функцию совместной вероятности $P(X_1,...,X_n)$ для $n$ событий или случайных величин $X_1,...,X_n$. Цепное правило: $$ P(X_1,...,X_n) = P(X_1)\cdot P(X_1\to X_2)\cdot P(X_1,X_2\to X_3)\cdot....\cdot P(X_1,X_2,...,X_{n-1}\to X_n), $$ представим в виде направленного ациклического графа. Узлы графа - это случайные величины, а стрелки, входящие в данный узел, являются условиями в цепном тождестве. Так как в тождестве порядок аргументов в правой части можно выбирать произвольным образом, существует $n!$ различных графов, описывающих совместную вероятность. Ниже на первом рисунке приведен граф для $n=4$. Остальные 23 графа получаются перестановками узлов:

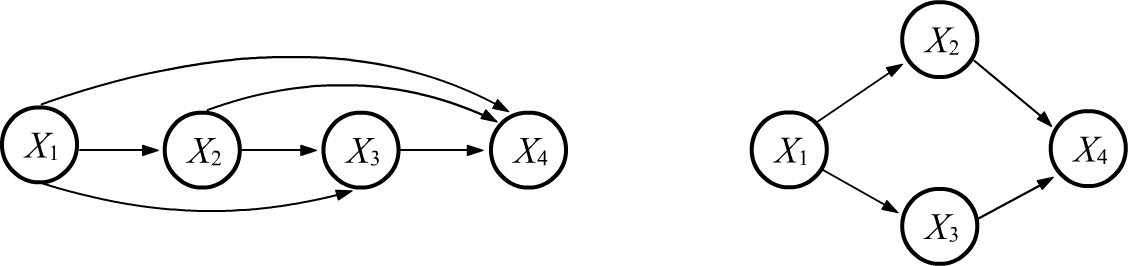
Если некоторые случайные величины являются условно независимыми, то граф упрощаётся (часть рёбер пропадает). Выше второй пример приведен для случая, когда $X_2$, $X_3$ условно независимы при наличии $X_1$, а для $X_4$ выполняется $P(X_1,X_2,X_3\to X_4)=P(X_2,X_3\to X_4)$, т.е. он условно независим от $X_1$. Совместная вероятность в этом случае имеет вид: $$ P(X_1,X_2,X_3,X_4) = P(X_1)\,P(X_1\to X_2)\,P(X_1\to X_3)\,P(X_2,X_3\to X_4). $$

Обычно сеть строится из соображений непосредственных причинных зависимостей случайных величин. После того как она построена, в каждом узле задаются условные вероятности $P(X_1,...,X_k\to X)$, где $X_1,...,X_k$ - входящие в узел $X$. Затем можно записывать совместную вероятность как произведение всех этих вероятностей. Имея совместные вероятности, можно получить ответ на любой вопрос о составных или условных событиях.

Фрэд и его сигнализация

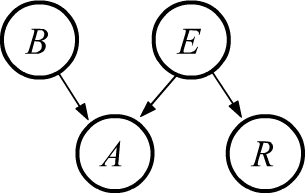Рассмотрим классический пример. Пусть Фрэд из Калифорнии установил в своём доме сигнализацию, которая может срабатывать, если произошло землетрясение (Earthquake).
Он едет в машине и получает уведомление о тревоге (Alarm). Слушая радио (Radio) он не слышит сообщения о землетресении (хотя его могли и не сделать). Какова вероятность того, что в дом забрался вор (Burglar)? Соответствующая байесова сеть приведена справа (на сигнализацию непосредственно может влиять грабитель или землетрясение, а на сообщение по радио - только землетрясение). Для этой сети совместная вероятность равна: $$ P(B,E,A,R) = P(B)\cdot P(E)\cdot P(B,E \to A)\cdot P(E\to R) = \frac{P(B,E,A)\,P(E,R)}{P(E)}. $$ Для её записи, перемножаются все узлы сети. Если в узел рёбер не входит (выше $B$ и $E$), то множитель будет равен вероятности величины: $P(B) P(E)$. Для узлов в которые входят рёбра, множителем служит условная вероятность, где условиями выступают величины от которых идут рёбра.

Фрэду известно, что произошло событие $A=a$ (была тревога) и $R=\bar{r}$ (по радио не было сообщения о землетрясении). И его интересует значение случайной величины $B$ (вор забрался в дом): $$ P(a,\bar{r}\to B) = \frac{P(B,a,\bar{r})}{P(a,\,\bar{r})}. $$ Совместные вероятности в числителе и знаменателе вычисляем, суммируя полную совместную вероятность $P(B,E,A,R)$ по отсутствующим переменным $E:\,\{e,\bar{e}\}$ и $B:\,\{b,\bar{b}\}$: $$ P(B,a,\bar{r}) = \sum_E P(B,E,a,\bar{r}),~~~~~~~~~~~~~P(a,\bar{r}) = \sum_{B,E} P(B,E,a,\bar{r}). $$ Если все условные вероятности на графе известны, несложно получить требуемую условную вероятность, подставляя в эти соотношения совместную вероятность $P(B,E,A,R)$.

Заметим, что безусловно независимыми событиями в этой задаче очевидно являются ($B$, $E$) и ($B$, $R$). Первая пара проверяется суммированием $P(B,E,A,R)$ по $R$ (сумма $P(E\to R)$ равна 1) и по $A$ (сумма $P(B,E \to A)$ равна 1). В результате получаем $P(B,E)=P(B)\cdot P(E)$. Аналогично доказывается независимость $B$ и $R$: $$ P(B,R) = \sum_{E,A} P(B,E,A,R) = P(B)\cdot \sum_{E,A} P(E)\cdot P(B,E \to A)\cdot P(E\to R) = P(B)\cdot \sum_{E} P(E)\cdot P(E\to R) $$ и далее: $$ P(B,R) = P(B)\cdot \sum_{E} P(E, R) = P(B)\cdot P(R). $$

Типы байесовых сетей

Рассмотрим сеть с тремя узлами. Если все они соединены стрелками (ниже первый рисунок), то независимых узлов (как в безусловном, так и условном смыслах) нет. Если части стрелок нет, появляются независимые узлы.

Примеры с вилкой и коллайдером были рассмотрены при введении условной независимости (мороженое и бросание костей). Докажем условную независимость для цепи. Соответствующая ей совместная вероятность равна $P(X,Y,Z)~=~P(X)\,P(X\to Y)\,P(Y\to Z)=P(X,Y)\,P(Y\to Z)$. Поэтому $$ P(Y\to X,Z) = \frac{P(X,Y,Z)}{P(Y)} =\frac{P(X, Y)\,P(Y\to Z)}{P(Y)} = P(Y\to X)\,P(Y\to Z). $$

Два множества узлов сети $\mathbb{A}$ и $\mathbb{B}$ являются условно независимыми при наличии множества узлов $\mathbb{C}$, если все пути между $\mathbb{A}$ и $\mathbb{B}$ разделены узлами $\mathbb{C}$.

Байесовская сеть называется причинной (казуальной), если во всех её связях $X_i\to X_j$ событие $X_i$ является причиной для появления события $X_j$. Задача с сигнализацией Фрэда является примером такого графа.