DemonScript: Работа с аксиомами
Введение
Для проведения логических выводов служит объект Mind. В него помещаются правила, сформулированные в виде аксиом: условие -> следствие. Движок логических выводов может работать как с трёхзначной логикой True, False, Undef, так и с более общей нечёткой логикой.
Родственные отношения
Опишем кровные родственные отношения при помощи следующих рёбер:
| X ancestor Y | - X является предком Y (не обязательно родителем) |
| X parent Y | - X является непосредственным кровным родителем Y |
| X child Y | - X является ребёнком Y |
edges ancestor, parent, child
Задание аксиом
Сообщим объекту Mind аксиомы, описывающие отношения:
Mind.add(
X !ancestor X, // антирефлексивно
X ancestor Z & Z ancestor Y -> X ancestor Y, // транзитивно
X parent Y -> X ancestor Y, // родитель - это предок
Y parent X -> X child Y, // определение ребёнка
Y child X -> X parent Y
)
Первая аксиома с отрицанием означает, что X не может быть сам себе предком.
Вторая аксиома - это свойство транзитивности - если X предок Z
и Z предок Y, то X будет предком Y.
Третья аксиома утверждает, что родитель также является предком.
Последние две аксиомы являются определением отношения "ребёнок", которое обратно к отношению "родитель".
Все аксиомы должны записываться в следующем формате:
A & !B & C ... -> D | !E | ...Слева от имликации (логического следствия) должны перечисляться отношения или их отрицания, связанные конъюнкцией (логическим И). Справа от импликации может стоять либо одно отношение, либо несколько, соединённых дизъюнкцией (логическим ИЛИ). Выражения типа A | B -> C или A -> B & C запрещены, однако их, при помощи булевой алгебры, всегда можно преобразовать к базовой форме.
Логический вывод
В DemonScript возможны различные методы проведения логических выводов. Рассмотрим простейший способ, когда в исходном графе с частично заданной информацией, устанавливаются все рёбра, следующие из аксиом. Пусть есть шесть людей:
nodes Ann, Bob, Liz, Jon, Mia, SamПредположим, что между ними существуют родственные отношения, изображённые на первом графе ниже (рёбра p - это parent, a - это ancestor). Однако, пока системе сообщим только часть информации, рёбра которой приведены на втором рисунке.
Ann ancestor Mia; Ann !ancestor Jon; Liz parent Mia; Mia parent Sam; Liz child Bob;
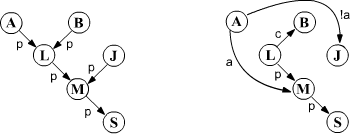
Запустим движок логических выводов, вызвав метод set_graph, которому передадим текущий граф GRAPH и после этого выведем рёбра этого графа:
Mind.set_graph(GRAPH) out GRAPHРезультат будет выглядить следующим образом:
GRAPH {
Ann{
ancestor: [ Mia, !Jon, !Ann, Sam],
parent: [!Ann, !Jon],
child: [!Ann, !Mia, !Sam],
},
Bob{
ancestor: [!Bob, Liz, Mia, Sam],
parent: [!Bob, Liz],
child: [!Bob, !Liz, !Mia, !Sam],
},
Liz{
ancestor: [!Liz, !Bob, Mia, Sam],
parent: [ Mia, !Liz, !Bob],
child: [ Bob, !Liz, !Mia, !Sam],
},
Jon{
ancestor: [!Jon],
parent: [!Jon],
child: [!Jon, !Ann, !Mia, !Sam],
},
Mia{
ancestor: [!Mia, !Ann, !Liz, Sam, !Bob, !Jon],
parent: [ Sam, !Ann, !Mia, !Liz, !Bob, !Jon],
child: [ Liz, !Mia, !Sam],
},
Sam{
ancestor: [!Sam, !Ann, !Mia, !Bob, !Liz, !Jon],
parent: [!Sam, !Ann, !Mia, !Bob, !Liz, !Jon],
child: [ Mia, !Sam],
},
}
Напомним, что знак восклицания перед именем объекта означает ложность отношения. Так, выше Ann parent Sam = False.
Часть установленных рёбер достаточно очевидна. Их антирефлексивности и транзитивности следует свойство асимметричности: (Y ancestor X) -> !(X ancestor Y) (если Y предок X, то X не может быть предком Y). Это свойство отношения ancestor привело к тому, что Ann !ancestor Ann и т.д. Так как родитель также является и предком, асимметричность автоматически распространилась и на отношение parent (сам себе не родитель). Мы указали, что Liz является рёбёнком Bob. Отсюда был сделан вывод, что Bob является родителем Liz. После этого было установлено, что Bob является также предком Liz, Mia, Sam.
Немного математики
Несколько хитрее ситуация с запретом Sam быть предком Jon. Кроме введенных в Mind аксиом используются также все их возможные трансформации. Напомним, что в булевой алгебре выполняется закон двойного отрицания, правило де-Моргана и справедливо следующее определение импликации:
!!A = A, ! (A & B) = !A | !B, A -> B = !A | B.Поэтому формула вида A & B -> C может быть преобразована следующим образом:
!(A & B ) | C = !A | !B | C = !A | !!C | !B = A & !C -> !B.Таким образом, можно переставлять выражения "вокруг" импликации, ставя перед ними логическое отрицание. В частности, аксиома транзитивности, кроме своей базовой формы, объектом Mind используется также в виде:
(X ancestor Z) & !(X ancestor Y) -> !(Z ancestor Y).Поэтому для Sam и Jon имеем:
(X ancestor Sam) & !(X ancestor Jon) -> !(Sam ancestor Jon).Так как есть такой X=Ann для которого посылка оказывается истинной, истинно и следствие: !(Sam ancestor Jon) = True или (Sam ancestor Jon) = False.
Последовательность отношений (перед которым может стоять отрицания), соединённых дизъюнкциями, наывается конъюнктивной нормальной формой (КНФ):
A | !B | !C | D | ...Фактически все аксиомы, в форме A & !B & ... -> C | !D это и есть КНФ вида !A | B | ... C | !D.
Аксиома двух родителей
В введенной системе аксиом не хватает ещё одного правила, о том, что у данного W не может быть более двух родителей. Этот факт можно отразить двумя способами. Добавим следующую аксиому (метод add можно вызывать любое число раз):
Mind.add( X parent W & Y parent W & Z parent W -> X==Y | X==Z | Y==Z )В этой аксиоме утверждается, что если у W есть родители X,Y,Z, то либо X равно Y, либо X равно Z, либо Y равно Z.
Проверим её работу, добавив в факты информацию о том, что Jon является родителем Mia:
Jon parent Mia; out Ann parent Mia // Является ли Ann родителем Mia? > Undef Mind.set_graph(GRAPH) out Ann parent Mia // Является ли Ann родителем Mia? > FalseДо проведения логических выводов отношение Ann parent Mia имеет неопределённое значение, т.к. Ann в принципе может быть родителем Mia. После вызова set_graph, на основании того, что у Mia уже есть два родителя, Mind сделает что Ann не является родителем Mia.
Использование демонов
В аксиомах кроме отношений, можно использовать демоны. При логическом выводе, они могут сообщать различную информацию об отношениях, которую сложно выразить чисто логическими методами.
def all_parents(X) // У X есть все родители
{
return X.count_in(parent) == 2
}
def undef_parent(X,Y) // Неопределено, что X является родителем Y
{
return (X parent Y) == Undef
}
Mind.add( undef_parent(X,Y) & all_parents(Y) -> !(X parent Y) )Таким образом, вместо аксиомы с 4-мя переменными о двух родителях, мы имеем такую же аксиому, но с двумя переменными. К тому, же она легко обобщается на любое число родителей.
Отцы и матери
Методы Mind
- Mind.add() - добавить аксиому или список аксиом, перечисленных через запятую. Все переменные, использующиеся в аксиомах должны быть объявлены выше при помощи оператора var. Каждая аксиома должна быть в конъюнктивной нормальной форме: A | B | !C | !D | E | ... или в эквивалентном виде с использованием импликации: !A & C & !E & ... -> B | !D (слева только конъюнкции, справа - только дизъюнкции).
- Mind.set_graph(G) - установить все рёбра в графе G в соответствии с аксиомами. В частности, G может быть текущим графом GRAPH (параметр обязателен).
- Mind.get_models(G, E, MAX_NUM=10) - получить все возможные модели. Возвращает массив графов, которые получаются из графа G всеми возможными (и разрешёнными аксиомами) установками ребра типа E в True или False. Последний параметр ограничивает число моделей (по умолчанию десятью). Если MAX_NUM=0 - ограничений нет. Пример вызова: var Models = Mind.get_models(GRAPH, in, 0).
- Mind.count_models(G, E) - поcчитать число всех возможных моделей (см. метод .get_models). Возвращает число, а не массив и не имеет ограничения по максимальному числу моделей. Пример вызова: out Mind.count_models(GRAPH, in)
- Mind.validator(demon(G)) - задание валидатора для методов get_models() и count_model(). Валидатор - это демон с одним аргументом типа граф. Он должен возвращать логическое значение. Если валидатор для данного графа G не возвращет True, то модель считается не верной и не помещается в список моделей для get_models или в число возможных моделей для count_models. Пример использования см. в "города и дороги".
- Mind.value(Models, Expr) - вычисление логического значения Exprs по массиву возможных моделей Model, который может быть получен методом get_models. Если во всех моделях это выражение имеет одно и тоже заначение, оно и возвращается методом. Если значение от модели к модели меняется, то метод возвращает Undef. Пример вызова: Mind.value(Models, A r B), см. также "города и дороги".
- Mind.verbose(level=0) - установить режим отладки логического вывода. Если level=1 - аксиома выводится когда она "срабатывает" и даёт новое значение для отношения. Если level=2, то происходит вывод промежуточных моделей в методах get_models, count_models. По умолчанию level=0 (ни чего не выводится).
- Mind.out() - вывести аксиомы Mind в его внутреннем представлении вместе с числом использований каждой аксиомы при логическом выводе.
- Mind.set_mode(1) - задать номер моды логического вывода. Если аргумент равен 1 - проводится работа с трёхзначной логикой (это быстрее). Если аргумент равен 2 - то вывод проводится в рамках нечёткой логики (пока в работе).
- Mind.clear_used() - очистить счётчик использования каждой аксиомы. Он находится в колонке used при выводе списка аксиом методом .out()
- Mind.clear() - очистить список всех аксиом.