Множество интерпретаций
Множество интерпретаций
Пусть задана сигнатура предметной теории. Представим (если сможем) множество интерпретаций \(\mathbb I\), элементами которого являются различные предметные множества и интерпретации на них. Два одинаковых предметных множества, на которых по-разному определены функции и предикаты, являются различными элементами множества интерпретаций. Будем считать, что любая формула, не содержащая свободных переменных, в данной интерпретации или истинна или ложна. Тогда на множестве \(\mathbb I\) существует подмножество истинности такой формулы.
Теория, предметные аксиомы \(A_1\), \(A_2,...\) которой пересекаются на множестве \(\mathbb I\), является непротиворечивой (существуют интерпретации на которых аксиомы одновременно выполнимы). Формулы теории \(T_1,T_2,T_3,...\), логически следующие из аксиом, содержат в себе область пересечения аксиом в качестве подмножества. Ниже на левом рисунке приведена теория в которой \(A_1,A_2 \Rightarrow T_1, T_2, T_3\). Кроме этого \(T_1\Rightarrow T_2\), однако из \(T_1\) или \(T_2\) не следует \(T_3\):
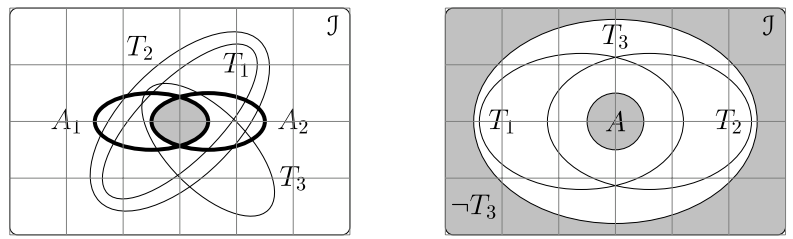
На правом рисунке условно изображён прямой вывод из аксиомы \(A\) формулы \(T_3\), с предварительным получением формул \(T_1\) и \(T_2\), которые покрывают большую область множества интерпретаций, чем \(A\). Затем из них получается \(T_3\): \(A~\Rightarrow~T_1,T_2~\Rightarrow~T_3\). Если формул, подобных \(T_1\) и \(T_2\) не существует, то приходится использовать метод от противного.
Не стоит путать множество интерпретаций и носитель интерпретации \(\mathbb X\), на диаграммах которого ранее иллюстрировались логические функции для предикатов и логическое следование. Любая подобная диаграмма является одной из возможной интерпретаций, т.е. элементом множества всех интерпретаций. Общелогические аксиомы покрывают всё множество интерпретаций.
Множество интерпретаций очень "большое" множество и допущение его существования является достаточно нетривиальным утверждением, требующим доказательства его непротиворечивости. Но даже использование его конечного подмножества часто оказывается эффективным методом установления возможных взаимоотношений между формулами.
Логический вывод
Любой нетривиальный логический вывод увеличивает множество истинности. Рассмотрим, например, вывод \(\forall_x\,P(x)~\Rightarrow~\exists_x\,P(x)\) на множестве из двух элементов \(\mathbb X=\{a,b\}\). На нём возможно 4 интерпретации, т.е. 4 способа задания истинности \(P(a)\) и \(P(b)\):
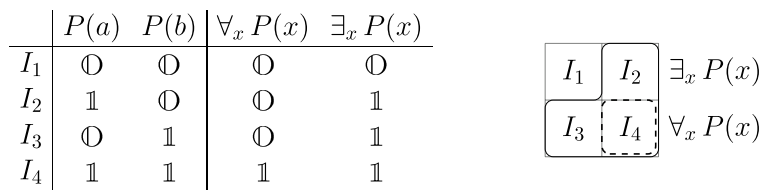
Так, в интерпретации \(I_2\) считаем, что \(P(a)\equiv \T\), \(P(b)\equiv \F\) и т.д. Посылка вывода (формула \(\forall_x\,P(x)\)) истинна только в интерпретации \(I_4\) (пунктир на рисунке), тогда как следствие (формула \(\exists_x\,P(x)\)) — в трёх интерпретациях (сплошная линия).
В реальной предметной теории множества истинности формул достаточно затейливо пересекаются. При этом возникают различные взаимосвязи между формулами (возможность логического вывода одних формул из других). Эти взаимосвязи можно отражать на графе логических следствий. Рассмотрим модельный пример с четырьмя формулами \(A\), \(B\), \(C\), \(D\), множества истинности которых изображены ниже на рисунке:
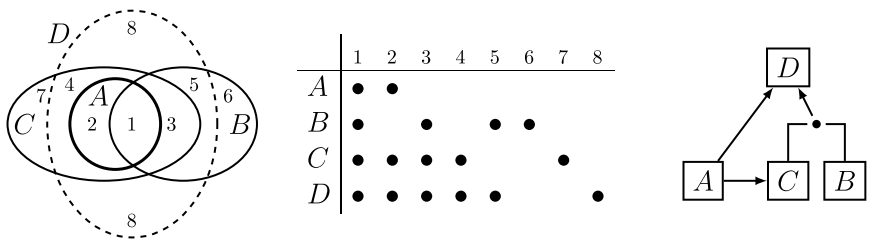
Объединение множеств \(A,B,C,D\) состоит из 8-и непересекающихся областей, номера которых приведены на рисунке. В таблице точками помечены формулы, множества истинности которых попали в ту или иную область. Так, в области 1 пересекаются все четыре формулы.
Последним нарисован граф логических следствий. Множество истинности формулы \(A\) является подмножеством \(C\), поэтому \(A\Rightarrow C\), что на графе помечено стрелкой от \(A\) к \(C\). Пересечение \(B\) и \(C\) — подмножество \(D\), поэтому \(B\,\&\,C~\Rightarrow D\). На графе это соответствует соединению в узле в виде точки линий от \(B\) и \(C\) с дальнейшей стрелкой от точки к \(D\).
Несложно видеть, что в этом примере в качестве системы независимых аксиом могут быть выбраны формулы \(A\) и \(B\), из которых выводятся \(C\) и \(D\). В общем случае систем аксиом может быть более одной.
В качестве двух примеров, использования интерпретаций, рассмотрим геометрию на плоскости и теорию групп.
Геометрия на плоскости
\(\rhd\) Запишем 2 аксиомы геометрии на языке с сигнатурой из множеств \(\mathbb P\) (точки), \(\mathbb L\) (прямые) и предикатов \(x\in \alpha\) (принадлежность), \(x=y\):
\(({\bf A_2})\): \(\forall_{\alpha}\,\exists_{x,y}\,(x\in\alpha~\,\&\,~y\in\alpha ~\,\&\,~ x\neq y)\) — На каждой прямой лежат две различные точки.
Для доказательства непротиворечивости аксиом, достаточно найти интерпретацию, где они обе истинны (т.е. их области истинности пересекаются). Это так, когда в \(\mathbb P=\{a,b\}\) два элемента, а в \(\mathbb L=\{\gamma\}\) — один и задано \((a\in\gamma)\equiv \T,~~ (b\in\gamma)\equiv \T\) (ниже 1-й рисунок):
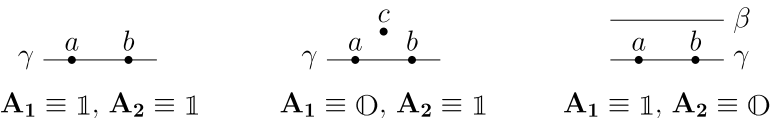
На 2-м и 3-ем рисунках даны интерпретации, доказывающие независимость аксиом (одна истинна, вторая — ложна, т.е. ни одна не является подмножеством другой). При этом, рисунки не имеют "геометрического смысла" и служат лишь для перечисления элементов множеств и значений предикатов. Например 3-й — это множество \(\mathbb P =\{a,b\}\), \(\mathbb L =\{\beta,\gamma\}\), где задано \((a\in\beta)\equiv (b\in\beta)\equiv \F\), \((a\in\gamma)\equiv (b\in\gamma)\equiv \T\). \(\square\)
Теория групп
\(\diamond\) Пусть определён предикат равенства \(x=y\). Введём предметную функцию \(f(x,y)\), которую будем записывать как \(x\cdot y\). Зададим аксиомы, определяющие свойства этой функции:
\[ \begin{array}{llll} ({\bf D}):~~~ &\forall_{x,y}\,\exists_z\, [x\cdot y=z], & ~~~~& определённость, \\ ({\bf A}):~~~ &\forall_{x,y,z} \,~~[(x\cdot y)\cdot z = x\cdot (y\cdot z) \bigr], & & асоциативность. \end{array} \]
В не операционной записи аксиома ассоциативности имеет вид \(f(f(x,y),z)=f(x,f(y,z)\). Интерпретации (множества на которых задана функция \(x\cdot y\)), где эти аксиомы выполняются (истинны), называют полугруппами.
Введём предметную константу \(e\) (выделенный единичный элемент) и добавим ещё две аксиомы:
\[ \begin{array}{lllll} ({\bf E}):~~~&\forall_{x}\,~~~[(x\cdot e=x) ~\&~(e\cdot x=x)], & ~~~& единичный~элемент, \\ ({\bf\, I\,}):~~~&\forall_x \exists_y \, [(x\cdot y = e)~\&~ (y\cdot x= e) ], & & обратный~элемент. \end{array} \] Число интерпретаций, удовлетворяющих такой расширенной системе аксиом, уменьшается. Изучением их свойств занимается теория групп. Наконец, если добавить ещё одну аксиому:
\[ \begin{array}{lllll} ({\bf S}):~~~~&\forall_{x,y}\,[x\cdot y = y\cdot x],& ~~~~~~~~~~~~~~~~~~~~~&функция~симметрична, \end{array} \]
подходящих интерпретаций станет ещё меньше ( абелевы группы). \(\square\)
Рассмотрим примеры интерпретаций аксиом теории групп и докажем их независимость. Предикат равенства \(x=y\) будем считать истинным, если \(x\) и \(y\) — это один и тот же элемент множества \(\mathbb X\). При таком определении, для задания интерпретации остаётся только перечислить значения функции группового умножения и выбрать единичный элемент. Для одноэлементного множества \(\mathbb X=\{e\}\) единственная и тривиальная интерпретация, удовлетворяющая всем аксиомам — это: \(e\cdot e=e\). Для двухэлементного множества \(\mathbb X=\{e,a\}\), существует 16 таблиц, определяющих функцию \(x\cdot y\) (считаем, что (\({\bf D}\)) выполняется). С точностью до переобозначения элементов, различных таблиц 10. Три из них приведены ниже:
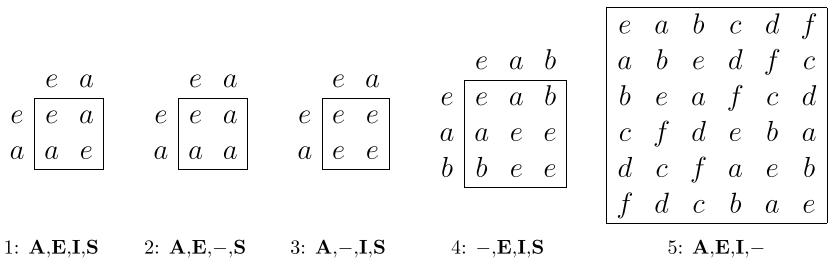
Строчки в таблицах соответствуют первому аргументу функции \(x\cdot y\), а колонки — второму. На пересечении строки и колонки, внутри рамки стоит значение функции. Например, первая таблица определяет функцию следующим образом: \(e\cdot e=a\cdot a=e\) и \(e\cdot a=a\cdot e=a\). Везде выделенный (единичный) элемент обозначен как \(e\).
Первая таблица удовлетворяет всем четырём аксиомам \(({\bf A},{\bf E},{\bf I},{\bf S})\), что доказывает их непротиворечивость (интерпретация \(\mathbb X=\{e\}\), \(e\cdot e=e\) — также это доказывает). Для следующей таблицы не выполняется аксиома \(({\bf I})\), так как у \(a\) нет обратного элемента. Остальные аксиомы выполняются, поэтому \(({\bf I})\) независима от \(({\bf A},{\bf E},{\bf S})\). Аналогично, третья таблица доказывает независимость аксиомы \(({\bf E})\).
Для доказательства независимости аксиомы ассоциативности \(({\bf A})\) необходимо уже взять трехэлементное множество \(\mathbb X=\{e,a,b\}\) с функцией группового умножения, приведенной в четвёртой таблице. Для неё, например \((b\cdot a)\cdot a\neq b\cdot (a\cdot a)\). Остальные же три аксиомы истинны.
Чтобы доказать независимость аксиомы симметричности \(({\bf S})\), необходимо множество \(\mathbb X\) с 6-ю элементами, которое допускает первую, самую маленькую неабелеву группу \({\bf D_3}\) (последняя таблица группового умножения с опущенными подписями у строк и столбцов). В этой группе (интерпретации), например, \(f\cdot d=a\) и \(d\cdot f = b\), т.е. \(({\bf S})\) не выполняется.
Отметим, что сигнатура теории групп может быть другой. Например, содержать выделенную константу "\(e\)" (единица) функцию \(i(x)\), дающую обратный элемент. Тогда в аксиомах квантор существования не понадобится.