Формализация математики
Введение
В математике аксиомы определяют объекты и их свойства. Новые утверждения (теоремы) доказываются при помощи логических рассуждений. Подобная схема впервые проявилась в книгах Евклида, в частности, при описании геометрии.
Пятая аксиома о параллельных прямых (не имеющих общей точки) выглядела сложнее остальных аксиом: "через всякую точку, не лежащую на данной прямой, проходит только одна, параллельная ей прямая". На протяжении более двух тысячелетий длилась безрезультатная борьба за её доказательство (вывод из остальных аксиом). Пятая аксиома оказалась всё же независимой, однако попытки построить её доказательство привели к неевклидовым геометриям и более глубокому пониманию как структуры математического здания, так и возможных свойств физического пространства.
Впрочем, на самом деле "доказательств" было множество. Внешне они выглядели безупречными, однако при более внимательном рассмотрении выяснялось, что в них неявно используется то или иное очень "естественное" допущение. Например, что может быть "очевиднее" существования треугольников со сколь угодно большой площадью? Однако нет ничего более неочевидного, чем очевидные истины.
Со временем возникла потребность так формализовать теории и методы доказательств, чтобы ни какие незаметно привнесённые "очевидности" не портили её логической стройности. В частности, по-возможности необходимо отказаться от естественного языка с присущей ему неоднозначностью. Блестящим примером подобного подхода явились "Основания геометрии" и последующие работы Давида Гильберта.
Формализация геометрии
Геометрия на плоскости родилась из построений при помощи линейки и циркуля. С формальной точки зрения это теория о точках и прямых. Эти сущности или предметы не наделяются образными свойствами ("не имеет ширины" и т.п). Просто рассматриваются объекты двух видов. Первые обозначаются латинскими буквами \(x\), \(y\),... и называются точками, а вторые — греческими \(\alpha\), \(\beta\),... и называются прямыми.
Предметы вступают в определённые отношения, которые в геометрии соответствуют словам "лежать", "параллельны", "между" и т.д. Чтобы избежать неоднозначности естественного языка, эти отношения записывают при помощи формальных обозначений. Например, фразы "точка \(x\) лежит на прямой \(\alpha\)" или "прямая \(\alpha\) проходит через точку \(x\)" кодируются функцией с именем "\(\in\)". Она имеет два аргумента. Первый — имя точки, а второй — имя прямой: \(\in(x,\alpha)\).
Для данных \(x\) и \(\alpha\) такая функция считается либо истинным утверждением (если \(x\) действительно принадлежит \(\alpha\)), либо ложным (в противном случае). Подобные логические функции, значения которых бинарны (истина/ложь) называются предикатами. Их аргументы — это предметные величины, т.е. сущности с которыми оперирует теория. В случае плоской геометрии это точки и прямые.
Предикаты с двумя аргументами часто записывают в операционном виде, когда имя предиката помещается между его аргументами как операция. Так, \(x \in \alpha\) — это то-же, что и \(\in(x,\alpha)\).
При помощи одних предикатов (отношений между объектами = логических функций = высказываний об объектах) можно определять другие. Для этого вводятся формальные замещения слов "И", "ИЛИ", "НЕ":
\(A \vee B\) : "ИЛИ" (или \(A\), или \(B\), или оба, т.е. хотя бы одно);
\(\neg A \) : "НЕ" (не \(A\); если \(A\) истинно, то \(\neg A\) — ложно).
Например, предикат от трёх сущностей: "прямая \(\alpha\) проходит через две точки \(x\) и \(y\)" можно определить следующим образом:
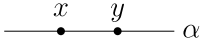 \[
L(x,\, y,\, \alpha)~~:~~~~(x \in \alpha) \, \& \, (y \in \alpha).
\]
\[
L(x,\, y,\, \alpha)~~:~~~~(x \in \alpha) \, \& \, (y \in \alpha).
\]
Двоеточие означает, что везде, где встречается \(L(x,\, y,\,\alpha)\), его необходимо заменить на строку \((x \in \alpha) \, \& \, (y \in \alpha)\).
Введём ещё два символа — заменители слов:
\(\exists\) : "существует по крайней мере один" = квантор существования
Теперь можно записывать различные геометрические утверждения. Например, фраза "для любых точек \(x\) и \(y\) существует по крайней мере одна прямая \(\alpha\), которая через них проходит" имеет вид: \[ \forall_x\, \forall_y\, \exists_\alpha\, L( x,\, y,\,\alpha), \] а предикат параллельности прямых \(\alpha\) и \(\beta\) определим как: \[ \alpha||\beta:~~~~\neg\exists_x\,(x\in\alpha~\&~x\in\beta). \]
Подобным образом записываются все аксиомы геометрии. Затем с ними проделываются формальные манипуляции для вывода новых формул. После перечисления аксиом и правил вывода, содержательная составляющая теории отходит на второй план. Построение доказательств и их проверка может быть проведена компьютером или марсианином, ничего не знающим о смысле букв \(x\), \(y\), \(\alpha\), \(\beta\), предиката \(x \in \alpha\), и ему подобных. Довнесение "очевидных" суждений, не заложенных в исходные аксиомы, при таком подходе уже практически невозможно.
Формализация арифметики
В каждой формальной теории фиксируется множество символов, при помощи которых записывают все утверждения. Так, для формулировки большинства фактов из теории натуральных чисел достаточно такого " алфавита": \[ 0~~1~~x~~+~~\cdot~~=~~(~~)~~\neg~~\&~~\vee~~~\forall~~~\exists \] Символы "\(0\)", "\(1\)" являются предметными константами, обозначающими числа "ноль" и "один", "\(x\)" — переменная (произвольное число). Дополнительные переменные можно ввести при помощи повторений \(xx\), \(xxx\), и т.д., которые для краткости обозначают как \(x, y,...\) или \(x_1, x_2,...\).
Сложение "+" — это предметная функция двух переменных. Каждым двум числам она ставит в соответствие третье число: \(+(x,y)\) или \((x+y)\). При помощи константы "\(1\)" и функции "\(+\)" определяется множество других констант: \(2:~(1+1),~3:~((1+1)+1)\), и т.д. Аналогично, точка — это ещё одна функция \(x\cdot y\), имеющая смысл умножения чисел.
Символ "=" — это предикат, истинный или ложный, в зависимости от того, равны числа или нет: \(2=2\) — это истина, \(1=2\) — это ложь.
Скобки, логические функции "\(\neg~ \& ~\vee\)" (НЕ, И, ИЛИ) и кванторы - заменители слов "все" ( \(\forall\) ) и "существует" ( \(\exists\) ) - позволяют записывать произвольные формулы. Таким образом, математическое утверждение представляется строкой символов из данного алфавита.
Существуют простые способы (алгоритмы) отличить правильно построенную формулу: "\(\neg(x=y) \vee (x+1=y)\)" от неправильной: "\(\vee)\neg\&x\)". Правильность понимается в смысле "синтаксически верно", а не в смысле истинно! Так, компилятор распознает синтаксическую ошибку, сделанную при записи программы, хотя синтаксически верная программа может работать и не правильно, например, никогда не останавливаться.
Через предикат \(x=y\) определяются предикаты "не равно" и "меньше":
\(x < y\) : \(\exists_z\, \bigl(z\neq 0 ~\&~ z+x=y\bigr)\).
В последнем случае предикат \(x < y\) истинен, если существует отличное от нуля число \(z\), добавление которого к \(x\), даёт \(y\). Двоеточием везде обозначается определение формулы или утверждения.
Аналогично можно определить предикаты \({\mathrm{Even}}(x)\): "\(x\) — чётное число" и \({\mathrm{Odd}}(x)\): "\(x\) — нечётное число": \[ {\mathrm{Even}}(x) ~:~ \exists_y \bigr( x = y + y\bigr),~~~~~~~~~~~~~{\mathrm{Odd}}(x) ~:~ \exists_y \bigr( x = (y + y)+1\bigr), \] т.е. число чётное, если существует \(y\), который при сложении с собой даёт \(x\). В этом определении не указывается как искать \(y\). Однако, если такой \(y\) находится (хотя бы один), предикат \(\mathrm{Even}(x)\) считается истинным.
Аксиомы теории
Предметные функции и предикаты определяются при помощи аксиом — формул, которым они должны удовлетворять (быть истинными).
\(\diamond\) Сложение в арифметике определяют аксиомы: \[ \begin{array}{lllll} \forall_x\,\bigr[\,x+1\neq 0\,\bigr],&~~~~~&\forall_x\,\forall_y\,\bigr[\,x+1\,\neq\, y+1~~\vee~~x=y\,\bigr],\\[2mm] \forall_x\,\bigr[\,x+0 = x\,\bigr], &~~~~~~&\forall_x\,\forall_y\,\bigr[\,x+(y+1)=(x+y)+1\,\bigr],\\ \end{array} \] а умножение: \[ \begin{array}{lllll} \forall_x\,\bigr[\,x\cdot 0 = 0\,\bigr], &~~~~~~~~~&\forall_x\,\forall_y\,\bigr[\,x\cdot(y+1)=(x\cdot y)+x\,\bigr].\\ \end{array} \] Предикат, утверждающий что число \(x\) является простым, имеет вид: \[ \mathrm{Prime}(x):~~~\neg\exists_y\exists_z\,\bigr[\,y\neq 1~\&~z\neq 1~\&~x=y\cdot z\bigr]. \] Это уже определение, использующее функцию умножения. \(\square\)
Кроме аксиом, задаются правила вывода — формальные способы получения одних формул из других. Такие правила сохраняют истинность выражений, так что из истинной формулы может быть выведена только истинная формула.
Свободные и связанные переменные
В формулах необходимо различать свободные и связанные предметные переменные. Связанная переменная стоит под действием квантора "\(\exists_x\) " или "\(\forall_x\)". Если рассматривается конечная предметная область, состоящая только из трех предметных констант \(x = \{1,2,3\}\), то: \[ \exists_x A(x) = A(1) \vee A(2) \vee A(3),~~~~~~~~~~~~~\forall_x A(x) = A(1) \,\&\, A(2) \,\&\, A(3). \] Первое выражение утверждает, что "существует такой \(x\), что некий предикат \(A(x)\) истинен". Это значит, что истинно или \(A(1)\), или \(A(2)\), или \(A(3)\) (хотя бы что-то одно из \(\{1,2,3\}\), которое и "существует"). Аналогично для квантора "любой" истинными должны быть и \(A(1)\), и \(A(2)\), и \(A(3)\), т.е. все. Таким образом, наличие в формуле переменной, связанной с квантором, аналогично индексу суммирования и выражение (после явной записи "суммы") от нее не зависит. Как и суммационный индекс, связанную переменную можно обозначить любой буквой, которой еще нет в выражении.
Формулы без свободных переменных считаются либо истинными, либо ложными. Например, утверждение об отсутствии самого большого простого числа: \[ \neg\exists_x\forall_y\,\bigr[\,\mathrm{Prime}(x)~\&~\mathrm{Prime}(y)~\&~y\leqslant x\,\bigr] \] истинно, а его отрицание (наибольшее число \(x\) существует) — ложно.
Прежде чем подробнее изучать введенные понятия, напомним основные факты из теории множеств.