Нормальные формы

КНФ

Для доказательства истинности некоторого выражения, его можно привести к конъюнктивной нормальной форме (КНФ). Чтобы это сделать, сначала избавляются от связок эквивалентности и импликации: \[ A\equiv B~~\Leftrightarrow~~(A\to B)\,\&\,(B\to A),~~~~~~~~~~~~~~~A\to B~~\Leftrightarrow~~\neg A\vee B. \] Затем, применяя несколько раз правила де-Моргана: \[ \neg(A \, \& \, B) ~~\Leftrightarrow~~ \neg A \vee \neg B,~~~~~~~~~~~~~~~~~~ \neg(A \vee B) ~~\Leftrightarrow~~ \neg A \,\&\, \neg B \] и закон двойного отрицания \(\neg(\neg A)~~\Leftrightarrow~~ A\), прижимают символ "\(\neg\)" к высказываниям, Наконец, при помощи дистрибутивности: \[ A \, \vee \, (B \,\&\, C) ~~~\Leftrightarrow~~~ (A \,\vee\, B) \,\&\, (A \,\vee\, C), \] логическому выражению придаётся следующий вид: \[ (A_1 \vee A_2 \vee ... ) \,\&\, (B_1 \vee B_2 \vee ... ) \,\&\, (C_1 \vee C_2 \vee ... ) \,\&\, ... \] Входящие в формулу буквы, являются простыми высказываниями (или предикатами), перед которыми, возможно, стоит отрицание "\(\neg\)". Это и есть конъюнктивная нормальная форма. Название происходит от соединения при помощи конъюнкций (логических "И") выражений, состоящих только из логических "ИЛИ". Так как операция \(\vee\) ассоциативна, скобки внутри дизъюнктов ("сумма" \(\vee\) в круглых скобках) можно не ставить.

Если формула тождественно истинна (=общезначима=тавтология), то каждый дизъюнкт также должен быть истинным. Поэтому выражение распадается на более элементарные: \[ A_1 \vee A_2 \vee ... ,~~~~~~~~B_1 \vee B_2 \vee ... ,~~~~~~~C_1 \vee C_2 \vee ..., \] каждое из которых должно быть истинным. Произойдёт это, если в каждом из них встретится некоторая буква и её отрицание (закон исключения третьего \(A\vee \neg A\)).

\(\diamond\) Докажем, что \((A\to B)\to (\neg B\to \neg A)\) — тавтология. Сначала избавимся от импликации "\(\to\)" и прижмём отрицание к высказываниям: \[ \neg(\neg A\,\vee\, B)~\vee~ (\neg\neg B\,\vee\, \neg A)~~~~~\Leftrightarrow~~~~~~(A~\&~\neg B)~\vee~ ( B\,\vee\, \neg A). \] Теперь воспользуемся дистрибутивностью: \[ \Leftrightarrow~~~~(\underline{A} \vee B\vee \neg \underline{A}) ~\&~(\neg \underline{\underline{B}} \vee \underline{\underline{B}}\vee \neg A). \] Каждая формула соединённая "\(\&\)", в силу закона "исключения третьего", — истинна. Первая содержит \(A\vee \neg A\), а вторая — \(B\vee \neg B\). \(\square\)

КНФ и аксиомы

Конъюнктивные нормальные формы играют важную роль при аксиоматическом построении теории, т.к. формулу, записанную в КНФ, можно разбить на более элементарные.

Если формула содержит кванторы всеобщности и существования, перед переводом её в КНФ, кванторы необходимо устранить. Для этого, при помощи кванторных тождеств, их действие распространяется на всю формулу. Запись \(\mathbb Q_x\mathbb Q_y \mathbb Q_z ... F\), где \(\mathbb Q\) это \(\exists\) или \(\forall\), а формула \(F\) не содержит кванторов, называется предварённой нормальной формулой.

Кванторы существования дают новые предметные константы и функции. Например, формула \(\exists_z \,\forall_x \,\exists_y \,A(x,y, z)\) заменяется на \(\forall_x\,A(x,\,f(x),\,a)\), где \(a\) — предметная константа (значение "существующего" \(z\)) и функция \(f(x)\) обозначает тот \(y\), который существует при каждом \(x\). После ликвидации кванторов \(\exists\), кванторы \(\forall\) опускаются: \(\forall_x\,A(x) ~~\Rightarrow~~ A(x)\) (если справедливо при любом \(x\), то справедливо и в каждом частном случае).

\(\diamond\) Пусть множество предметов \(\mathbb X\) состоит из людей и неодушевлённых сущностей. Введем предикат \(H(x):\) "\(x\) — человек" и \(M(x,y):\) "\(x\) является матерью для \(y\)". Сформулируем утверждение: "каждый человек имеет мать, которая также человек": \[ \forall_x\,\bigr[H(x)\to \exists_y\,\bigr(H(y)\,\&\,M(y,x)\bigr)\bigr]. \] Выразим импликацию через дизъюнкцию и расширим действие \(\exists_y\) на всю формулу: \[ \forall_x\,\exists_y\,\bigr[\neg H(x)\,\vee\, \bigr(H(y)\,\&\,M(y,x)\bigr)\bigr]. \] Для каждого \(x\) существует \(y\), поэтому введём предметную функцию \(m(x)\), дающую мать для сущности \(x\) и опустим квантор \(\exists_y\): \[ \forall_x\bigr[\neg H(x)\,\vee\, \bigr(H(m(x))\,\&\,M(m(x),x)\bigr)\bigr]. \] Воспользуемся дистрибутивностью: \[ \forall_x\bigr[\bigr(\neg H(x)\vee H(m(x))\bigr)\,\&\,\bigr(\neg H(x)\vee M(m(x),x)\bigr)\bigr]. \] По правилу объединения, можно написать \(\forall_x\, (A_x\,\&\,B_x)\equiv\forall_xA_x\,\&\,\forall_yB_y\), т.е. формула является конъюнкцией двух утверждений. Так она считается истинной, то независимо истинно и каждое утверждение. Поэтому получается две аксиомы предметной теории о людях и их матерях: \[ \neg H(x)\vee H(m(x)),~~~~~~~~~~\neg H(y)\vee M(m(y),y). \] Такое представление исходной аксиомы называют стандартной формой. Заметим, что в этом примере введение функции \(m(x)\) оправдано, так как предполагается, что мать у человека (в этой модели) может быть одна (хотя, это, вообще говоря, самостоятельная аксиома). \(\square\)

СКНФ

Иногда необходимо доказать совпадение таблиц истинности двух выражений, не перебирая значения всех переменных. Каждое из выражений можно записать в конъюнктивной нормальной форме. Однако в таком виде их ещё рано сравнивать, т.к. одна и та же формула может иметь различные КНФ. Например, \(A\,\&\, B\) эквивалентно \(A\,\&\, (A\vee B)\,\&\, (\bar{A}\vee B)\).

Для подобных задач, формулу, записанную в КНФ, представляют в совершенной конъюнктивной нормальной форме (СКНФ). Под этим подразумевается следующее. Если формула зависит, например, от трёх высказываний \(A\), \(B\) и \(C\), то каждая из этих букв должна встречаться один раз в каждой из скобок, соединённых логическим "И". Когда в дизъюнкте нет, скажем, буквы \(B\), то при помощи "ИЛИ" в него добавляется всегда ложная формула \(B\,\&\,\bar{B}\), не меняющая истинности выражения.

\(\diamond\) Например: \[ A\,\&\,B ~\Leftrightarrow~\bigr(A\vee (B\,\&\,\bar{B})\bigr)\,\&\,\bigl(B \vee (A\,\&\, \bar{A})\bigr). \] Дважды выполним преобразование дистрибутивности: \[ (A\vee B) \,\&\, (A\vee \bar{B})\,\&\,(\bar{A}\vee B) \] (второй дизъюнкт \(A\vee B\) опущен, т.к. он уже есть). \(\square\)

Если в СКНФ упорядочить все высказывания, например, по алфавиту, то получится однозначное выражение. Число переменных в сравниваемых выражениях должно совпадать. Поэтому перед построением СКНФ применяют правила поглощения, для исключения высказываний, значения которых не влияют на истинность выражения.

\(\diamond\) Например: \(A\,\&\,(A\vee B)\) по описанному алгоритму приводит к формуле \((A\vee B)\,\&\,(A\vee\bar{B})\), хотя и равно \(A\). \(\square\)

СКНФ по таблице истинности

Если две формулы имеют одинаковые СКНФ, то они имеют и одинаковые таблицы истинности. По таблице истинности можно построить СКНФ, тем самым получив соответствующее ей логическое выражение. Для этого необходимо:

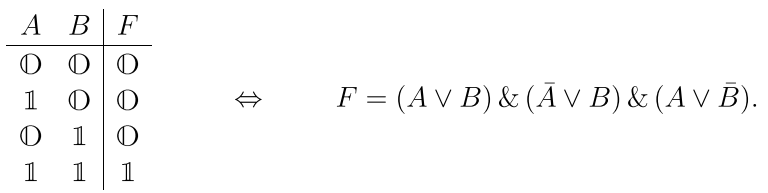
Такая формула правильно воспроизводит все строчки, дающие \(\F\) и автоматически истинна в остальных случаях.

Тавтология в СКНФ от высказываний не зависит (всегда равна \(\T\)), а ложная формула от \(n\) высказываний будет иметь \(2^n\) дизъюнктов.

ДНФ и СДНФ

Аналогично КНФ или СКНФ можно строить дизъюнктивную нормальную форму (ДНФ), и соответствующий ей совершенный вариант (СДНФ). При этом ДНФ определяется как выражение вида: \[ (A_1\,\&\,A_2\,\&\, ...)\vee (B_1\,\&\,B_2\,\&\, ...) \vee (C_1\,\&\,C_2\,\&\, ...)\vee..., \] где каждая буква является либо простым высказыванием (предикатом), либо его отрицанием. Таким образом, конъюнкция ("\(\&\)") и дизъюнкция ("\(\vee\)") меняются ролями. Преобразование к ДНФ проводится также как и к КНФ, но на финальном этапе используется другой закон дистрибутивности: \[ A \, \& \, (B \vee C) ~~~\Leftrightarrow~~~ (A \,\&\, B)\, \vee \, (A \,\&\, C). \] Соответственно, для построения СДНФ из ДНФ необходимо добавлять истинное выражение \(...\,\&\, (A\vee \neg A)\), которое не изменит истинностного значение конъюнкта, т.к. \(B \,\&\,\T \equiv B\).

ДНФ можно использовать для доказательства ложности некоторого выражения. Для этого должны быть ложными все конъюнкты, соединённые логическим "ИЛИ": \((A_1\,\&\,A_2\,\&\, ...)\) — ложно, \((B_1\,\&\,B_2\,\&\, ...)\) — ложно и т.д. Это, в свою очередь, происходит, когда в каждом из этих выражений встречается некоторая буква и её отрицание. Действительно, \(A\,\&\,\neg A\) ложно, а \(\F\,\&\,A\equiv \F\).

Алгоритм построения СДНФ по таблице аналогичен СКНФ: отбираются все строки равные \(\T\), а перед элементарными высказываниями ставится отрицание, если их значение равно \(\F\). Они соединяются при помощи \(\&\), а строки при помощи \(\vee\).

Упрощение формул

Приведение формулы к КНФ или ДНФ часто позволяет получить более простое выражение.

\(\diamond\) Рассмотрим в качестве примера: \(A\vee \bigl((A\to B)\,\&\, C\bigr)\). Выразим импликацию через дизъюнкцию: \[ A\vee \bigl((\bar{A}\vee B) \,\&\, C\bigr)~~~~\Leftrightarrow~~~~(A\vee \bar{A} \vee B) \,\&\, (A\vee C) ~~~~\Leftrightarrow~~~~A\vee C, \] где сначала применён закон дистрибутивности. Первый дизъюнкт содержит \(A\vee \bar{A}\), поэтому всегда истинен, и без изменения таблицы истинности первую скобку в выражении можно отбросить. В результате, исходная формула равна \(A\,\vee\,C\) и не зависит от \(B\). Это можно также проверить перебором значений в таблице истинности. \(\square\)

Иногда выражение сильнее упрощается в КНФ, а иногда в ДНФ, поэтому стоит строить оба представления. В примере с таблицей на предыдущей странице \(F = A\, \&\, B\) (СДНФ по последней строке).