ML: Logic and Probability: Theory Examples
Introduction
This document serves as an optional appendix to the introduction to
mathematical logic.
We will explore several formal theories,
analyzing their axioms and examples of logical inference.
Quantifiers and number of objects
✒ The phrase "there exist distinct objects in relation $R$" is written as: $$ \exists_{x,y}\,\bigr[x\neq y~\,\&\,~R(x,y)\bigr]. $$ The quantifiers $\exists_{x,y}$ c $x,y\in \{a_1,a_2,...\}$ "iterate" over disjunctions of formulas $\bigr[a_i\neq a_j~\,\&\,~R(a_i,a_j)\bigr]$ for pairs of objects. Terms with $i=j$ will be false: $(a_i\neq a_i) ~\equiv~\F $ and don't affect the result $\F \vee Q ~\leftrightarrow~ Q$. For three objects $\{a_1,a_2,a_3\}$, we get: $ R(a_1,a_2)\vee R(a_1,a_3)\vee R(a_2,a_1)\vee R(a_2,a_3)\vee R(a_3,a_1)\vee R(a_3,a_2), $ which is the meaning of the phrase.
✒ The phrase "any distinct objects are in relation $R$", requires an implication (if $x\neq y$, then ...): $$ \forall_{x,y}\,\bigr[x\neq y~\to~R(x,y)\bigr]. $$ The universal quantifier is a chain of formulas connected by conjunctions. For identical objects, terms like $a_1\neq a_1 ~\to~R(a_1,a_1)$ are true and can be omitted ($\T \,\&\,Q~\equiv~ Q$). Only pairs of distinct elements remain.
When translating from natural language to formal language,
one should not confuse implication and conjunction.
The phrase "for any positive $x$
property $P$ holds" is written as: $\forall_x\,[(0 \lt x)\, \to\,P(x)]$.
Using conjunction would lead to
$\,\forall_x\,[(0 \lt x)~\,\&\,~P(x)]$, which would be false in arithmetic
(due to $\forall_x$ at $x=0$).
The formula $\forall_x\,[(0 \lt x)~\vee~ P(x)]$ for $x\in \mathbb{N}=\{0,1,2,...\}$ would be equivalent to $P(0)$,
which is also incorrect.
If we say "there exists a positive $x$ with property $P$",
we write $\exists_x\,[(0\lt x)~\&~P(x)]$.
✒ The existential quantifier $\exists_x P(x)$ indicates that there is at least one object satisfying property $P$. Often, it's necessary to specify the exact number of objects mentioned in a statement.
The phrase "no more than one object ($0$ or $1$) satisfies property $P$",
is written as:
$$
\forall_{x,y}\,\bigr[P(x)\,\&\,P(y)~\to~x=y\bigr].
$$
Accordingly, the quantifier "exactly one object satisfies property $P$" can be defined as:
$$
\exists^1_x\, P(x)~~~~~~~~\Leftrightarrow~~~~~~~~\exists_z\,P(z)~~\&~~\forall_{x,y}\,\bigr[P(x)\,\&\,P(y)~\to~x=y\bigr].
$$
Now, the symbol $\exists^1_x$ can be used in formulas alongside other quantifiers.
Similarly, "at least two objects $(2,3,...)$ have property $P$" is written as:
$$
\exists_{x,y}\,\bigr[P(x)~\&~P(y)~\&~x\neq y\bigr],
$$
and "no more than two objects $(0,1,2)$ have property $P$" is written as:
$$
\forall_{x,y,z}\,\bigr[P(x)~\&~P(y)~\&~P(z)~\to~(x=y~\vee~x=z~\vee~ y=z)\bigr].
$$
The conjunction of these two formulas gives the phrase
"exactly two objects have property $P$", i.e. $\exists^2_x\,P(x)$.
Natural numbers
The set of objects with the properties of natural numbers, $\mathbb{N}=\{0,1,2,...\}$,
can be defined in a signature with the constant $0$
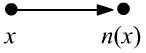
and a unary (single argument) function, which represents the number following $x$, denoted as $n(x)$.
We assume that the signature also includes the relation $x=y$ with standard properties (theory with equality).
Let $n(x)$ be a well-defined function, i.e., it satisfies the "zero axiom":
$~~~\forall_x\,\exists^1_y\,[\,n(x)=y\,]$.
To simplify the formulas, general quantifiers that span the entire formula will be omitted but are implied. The first two Peano axioms (PA) defining the function $n(x)$ are as follows:
$$ \begin{array}{llll} (\mathbf{N_1})& n(x) \neq 0 & ~~~~~ &-&\text{no number precedes 0} \\ (\mathbf{N_2})& n(x)=n(y) \to x=y & &-&\text{if the numbers are the same, the preceding numbers must also be the same} \\ \end{array} $$
Axioms can hold true for different interpretations
(including those based on finite sets).
In the diagrams, we represent objects (the "numbers") as dots,
and the function $n(x)$ as arrows connecting
$x$ and its value $n(x)$. Since $n(x)$ is defined for all $x$,
from each point, exactly one arrow must always emerge (well-defined function).
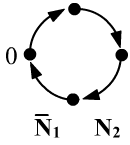Axiom ${\mathbf N_1}$ does not hold in interpretations
where a finite number of elements, including $0$, are connected in a loop,
since it is impossible to "reach" $0$
(the bar over ${\mathbf N_1}$ indicates it does not hold). Axiom ${\mathbf N_2}$
is true in this interpretation.
Therefore, ${\mathbf N_1}$ is not derivable from ${\mathbf N_2}$.
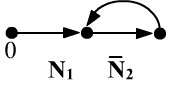
Axiom ${\mathbf N_2}$ forbids two or more arrows from converging at the same point.
The diagram on the right shows that ${\mathbf N_1}$ holds, but ${\mathbf N_2}$ does not,
indicating that the two axioms are independent of each other.
Both ${\mathbf N_1}$ and ${\mathbf N_2}$ only hold on infinite sets.
Below is a countable set of objects forming a model for ${\mathbf N_1}$ and ${\mathbf N_2}$.
This set is divided into four disjoint subsets: $\mathbb{N}_0\cup\mathbb{N}_1\cup\mathbb{Z}_1\cup\mathbb{C}_1$:
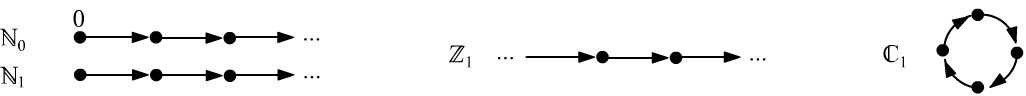
The sets $\mathbb{N}_0,\,\mathbb{N}_1$ are "one-directional" infinite "sequences," where $\mathbb{N}_0$ starts at zero, and $\mathbb{N}_1$ contains no zero. These can be "constructed" using rational numbers: $\mathbb{N}_0=\{0,\,1/2,...,\,n/(n+1),...\}$, $\mathbb{N}_1=\{1,\,1+1/2,...,\,1+n/(n+1),...\}$. The set $\mathbb{Z}_1$ has neither a beginning nor an end: $\mathbb{Z}_1=\{...,\,3-2/3,\,3-1/2,\,3,\,3+1/2,\,3+2/3,...\}$. The fourth set $\mathbb{C}_1$ is a loop of any finite number of elements.
To reason about infinite sequences, an additional axiom, called the Axiom of Mathematical Induction, is needed. It depends on an arbitrary predicate $P(x)$: $$ (\mathbf{I})~~~~~~~~~~~~~P(0)~\to~\bigr(\,\forall_x\,\bigr[P(x)\to P(n(x))\bigr]~~\to~~ \forall_x\,P(x)\,\bigr). $$ This is actually a "scheme of axioms," meaning an infinite set of formulas with any conceivable properties $P(x)$. By the rule of modus ponens (MP): $P,~P\to Q~\Rightarrow~Q$, this axiom is equivalent to the inference rule: $$ (\mathbf{Ind})~~~~~~~P(0),~~~~~\forall_x\,\bigr[P(x)\to P(n(x))\bigr]~~~~~\Rightarrow~~~~~ \forall_x\,P(x). $$ It means that if $0$ has the property $P$ (base of induction) and for any $x$ with property $P$, the next number $n(x)$ also has property $P$, then all numbers have property $P$.
We will show that the induction axiom forbids models like $\mathbb{N}_0\cup\mathbb{N}_1$ from the previous diagram, and therefore is independent of the axioms $\mathbf{N_1},\,\mathbf{N_2}$. More precisely, we will prove that sets like $\mathbb{N}_1$, where there is a nonzero element with no predecessor, are forbidden:
For any non-zero $x$ there is a number preceding it $y$.
$(1)$ In the base case $P(0)$ the premise $0\neq 0$ is false, so regardless of the conclusion, the implication $P(0)$ is true $(\F\to A\equiv \T)$.
$(2)$ $P(n(x))$ becomes $n(x)\neq 0~\to~\exists_y\,[\,n(y)=n(x)\,]$. No matter the value of $x$, the conclusion $\exists_y\,[\,n(y)=n(x)\,]$ is true because such a $y=x$ exists. Therefore, $P(n(x))$ is true, and since $A\to \T\equiv \T$ the implication $P(x)\to P(n(x))$ is true for any $x$. $\square$
Note that the axioms $\mathbf{N_1},~\mathbf{N_2}$ did not participate in this proof.
It is more difficult to exclude sequences like $\mathbb{Z}_1$ or $\mathbb{C}_1$, which do not include zero. Moreover, it can be proven that no matter what axiom system we choose, there will always exist interpretations that are not isomorphic to the standard model of natural numbers (these are known as non-standard models of arithmetic).
Addition and multiplication
Let’s add binary functions (with two arguments) for addition $x+y$ and multiplication $x\cdot y$ to the signature of natural numbers. Assume that the properties of addition are inductively defined by the following two axioms for all $x,y$: $$ (\mathbf{A_1})~~~~~~~~~x+0 ~=~ x,~~~~~~~~~~~~~~~~~~~(\mathbf{A_2})~~~~~~~~~ n(x+y) ~=~ x+n(y). $$ If in $\mathbf{A}_2$ we set $y=0$ and take into account $\mathbf{A}_1$, we get $n(x)=x+1$, where $1=n(0)$ is a new object constant, distinct from $0$ by axiom $\mathbf{N}_1$. Let’s add it to the signature. As a result, the axioms for addition and multiplication can be written in a more familiar form:
$$ \begin{array}{llll} (\mathbf{A_1})~~~ & x+0 ~=~ x,\\ (\mathbf{A_2})~~~& (x+y)+1 ~=~ x+(y+1),\\ \end{array} ~~~~~~~~~~~~~~~~~~~~~~~~ \begin{array}{llll} (\mathbf{M_1})~~~& x\cdot 0 ~=~ 0,\\ (\mathbf{M_2})~~~& x\cdot (y+1)~=~x+(x\cdot y).\\ \end{array} $$
The set of seven formulas $\mathbf{N_1},\mathbf{N_2},\mathbf{I},\mathbf{A_1},\mathbf{A_2},\mathbf{M_1},\mathbf{M_2}$
constitutes the system of Peano axioms (PA) for arithmetic.
As an example, let’s derive the commutativity and associativity of the addition function from these axioms.
Assume $P(x)$ holds. We will prove that $P(x+1)$ is also true by showing the following chain of equalities, annotating each step with the formula used: $$ (x+1)+0 ~~\overset{\bf A_1}{=}~~x+1 ~~\overset{\bf A_1}{=}~~(x+0)+1 ~~\overset{P(x)}{=}~~(0+x)+1 ~~\overset{\bf A_2}{=}~~0+(x+1). $$ The equality between the first term $(x+1)+0$ and the last term $0+(x+1)$ is the formula $P(x+1)$. Therefore, from axioms $\mathbf{A_1},~\mathbf{A_2}$, we derive $P(x)\to P(x+1)$, therefore the formula $\forall_x\,[\,P(x)\to P(x+1)\,]$ is derivable, and by the induction axiom $\mathbf{I}$, we derive $\forall_x\,P(x)$. $\square$
🔥 This proof is presented in algebraic style for brevity. A notation like $t_1=t_2=t_3$ is shorthand, equivalent to: $~~t_1=t_2,~~t_2=t_3~~~\Rightarrow~~~t_1=t_3$ (transitivity). The first equality is a consequence of axiom $\mathbf{A}_1$, which states (we now include the quantifier $\forall$, if applicable): $$ \forall_x\, (x+0=x)~~~~~\Rightarrow~~~~~x+0=x~~~~~\Rightarrow~~~~~(x+1)+0 = x+1, $$ where we applied the rules of inference $\forall_x\,Q(x)~~\Rightarrow~~Q(x)~~\Rightarrow~~Q(t)$ for the term $t=x+1$ (substitution). Thus, we have $\mathbf{A_1},~\mathbf{A_2},~P(x)~~\Rightarrow~~P(x+1)$, therefore $\mathbf{A_1},~\mathbf{A_2}~~\Rightarrow~~P(x)\to P(x+1)$. If a formula with a parameter follows only from the axioms of the theory, then we may apply the generalization rule (rule of generalization): $\text{Axioms}~~\Rightarrow~~~Q(x)~~\Rightarrow~~\forall_x\,Q(x)$. Indeed, if the formula $Q(x)$ with parameter $x$ follows from $\text{Axioms}$, then it must be true whenever the axioms are true, for any value of $x$.
Let's prove that $P(x)$ implies $P(x+1)$: $$ (y+(x+1))+1 ~~\overset{\bf A_2}{=}~~ ((y+x)+1)+1 ~~\overset{ P(x)}{=}~~ ((y+1)+x)+1 ~~\overset{\bf A_2}{=}~~ (y+1)+(x+1). $$ The equality of the first and last terms is the formula $P(x+1)$, hence $P(x)\to P(x+1)$. $\square$
$$ x+(y+1)~~\overset{\bf A_2}{=}~~(x+y)+1~~\overset{P(y)}{=}~~(y+x)+1 ~~\overset{\bf AC_1}{=}~~(y+1)+x.~~~\square $$
Note that in the set of axioms $({\bf N_1,N_2,I,A_1,A_2})$ there is no direct assertion about the commutativity of addition. This is somewhat surprising.
Let's now prove the associativity of addition:
Geometry
Let's consider, as a second example, a part of Hilbert’s axioms for plane geometry (two-dimensional geometry).
Assume there are two types of objects - points $x,y,...\in\mathcal{P}$ and lines $\alpha,\beta...\in\mathcal{L}$.
We do not assign them any visual or physical properties.
They are simply elements of two abstract sets $\mathcal{P}$ and $\mathcal{L}$.
There are no constants or functions in this theory.
The first predicate is the equality predicate for elements within the same set: $x=y$ or $\alpha=\beta$.
Inequality is defined using logical negation: the notation $x\neq y$ is shorthand for $\neg(x=y)$.
The second predicate $(x\in\alpha)$ in "informal geometry" corresponds to phrases
like: "the point $x$ lies on the line $\alpha$" or
"the line $\alpha$ passes through the point $x$".
For brevity, we’ll also use derived predicates:
$(x,y\in\alpha)$ stands for $~(x\in\alpha)\,\&\,(y\in\alpha)$ (meaning both points $x,\,y$ lie on line $\alpha$)
or $(x\in \alpha,\beta)$ stands for $~(x\in\alpha)\,\&\,(x\in\beta)$ (meaning lines $\alpha$ and $\beta$
intersect at point $x$).
Since a formal theory must not contain any "obvious" or implicitly assumed statements, the properties of the predicate $(x\in\alpha)$ must be defined explicitly through axioms.
Through any two points $x,y$ there exists a line $\alpha$ (possibly more than one) passing through both.
From this, it follows that through any point there is at least one line: $\forall_x \,\exists_\alpha \,(x\in\alpha)$, because the pairs $(x,y)$ in $\forall_{x,y}$ include diagonal pairs like $(x,x)$, which must also satisfy the axiom. This uses the rule $\forall_{x,y}\,A(x,y)~\Rightarrow\forall_x \,A(x,x)$.
Through any two distinct points $x,y$ at most one line ($0$ or $1$) can pass.
Together, $\mathbf{A_1}\,\&\,\mathbf{A_2}$ mean that through any two distinct points, there is exactly one line.
Each line $\alpha$ contains at least two distinct points $x,y$.
There exist at least three distinct points $x,y,z$ that do not lie on the same line $\alpha$.
The shorthand $x\neq y\neq z$ represents the conjunction of three predicates: $(x\neq y)\,\&\,(x\neq z)\,\&\,(y\neq z)$
and, as in the previous axiom, ensures that only distinct $x,y,z$ are considered under the existential quantifier.
This axiom requires at least three points and the existence of "two dimensions" (since axioms $\mathbf{A_1}$-$\mathbf{A_3}$
still hold even if all points lie on a single line).
It is not necessary for such a triple of points to exist for every line — one such triple is enough.
From $\mathbf{A_4}$, it follows that for any given line, there is at least one point that does not lie on it:
$\forall_\alpha\,\exists_x\,\neg(x\in \alpha)$.
Indeed, among the three points guaranteed by $\mathbf{A_4}$ either none lie on line $\alpha$,
or at most two do $\square$.
In principle, instead of axiom $\mathbf{A_4}$, one could take the formula $\forall_\alpha\,\exists_x\,\neg(x\in \alpha)$,
as, together with $\mathbf{A_3}$, it implies a stronger version of $\mathbf{A_4}$.
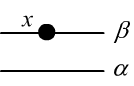To formulate the fifth axiom concerning parallel lines, we define a predicate with three arguments:
$$
\text{Par}(x,\alpha,\beta):~~~~~~(x\in\beta)~\,\&~\neg \exists_y (y\in\alpha,\beta)
$$
This means: "line $\beta$, which passes through point $x$, is parallel to line $\alpha$".
Parallelism is understood in terms of having no points in common ("there is no common point $y$ for lines $\alpha$ and $\beta$").
As with any predicate, this expression may be true or false depending on the values of its arguments.
For any point $x$ and any line $\alpha$, which $x$ does not belong to, there exists at most one ($0$ or $1$) line parallel to $\alpha$.
For the complete description of planimetry, we also need to introduce the "betweenness" relation $B(x,y,z)$: "point $y$ lies between points $x$ and $y$" and the congruence relation (geometric equality of segments and angles). Their properties are also defined by corresponding groups of axioms. From these axioms, the following theorem can be derived:
There must be at least one parallel line.
Therefore, together with axiom $\mathbf{A_5}$, we obtain the Euclidean statement $\mathbf{E}=\mathbf{A_5}\,\&\,\mathbf{T_5}$, which says that the line $\beta$ parallel to line $\alpha$ and passing through point $x$, which does not lie on $\alpha$, is always one and only one.
Analyzing the axioms of geometry
Let's demonstrate the consistency of the five geometry axioms formulated above for the relation $(x\in\alpha)$:
In the first figure (a model) all five axioms are true. It is important to emphasize that the diagram carries no geometric meaning and serves only as a listing of objects and the truth values of the predicate $(x\in\alpha)$. For example, the sets of points and lines are chosen as three-element sets: $\mathcal{P}=\{a,b,c\}$ and $\mathcal{L}=\{\alpha,\beta,\gamma\}$. The truth values of the predicate on these sets are defined so that $(b\in\alpha)\equiv (c\in\alpha)\equiv \T $, and $(a\in\alpha)\equiv \F $, etc. Since $\mathbf{A_5}$ allows for the absence of parallel lines ("at most one"), it is also true in this interpretation. However, Euclid’s theorem $\mathbf{E}$ is false (there are no parallel lines), which is indicated by a line drawn above $\mathbf{E}$. The second model is similar.
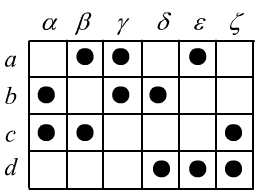
In the third model, there are four points and six lines : $\mathcal{L}=\{\alpha,\beta,\gamma,\delta,\sigma,\epsilon\}$. In this interpretation, all axioms $(\mathbf{A_1}-\mathbf{A_5})$ and $\mathbf{E}$ are true. The parallel lines are: $(\alpha,\epsilon)$, $(\beta,\delta)$ and $(\gamma,\sigma)$. Note that in the center, the lines do not intersect (only the black dots are considered points). The fourth model is isomorphic to the third.
Isomorphism of two models in this case means that there exist permutations of the points $x'=f(x)$ and lines $\alpha'=g(\alpha)$
such that $(x\in\alpha)~\leftrightarrow~(x'\in\alpha')$ for all $x$ and $\alpha$.
For example, the interpretation in the last image is described by the table shown to the right (a dot indicates the relation is true).
In this case, there are $720$ non-equivalent permutations of the table’s rows and columns,
and therefore, $720$ isomorphic interpretations.
Let's present interpretations that demonstrate the independence of the axioms $(\mathbf{A_1}-\mathbf{A_5})$ (the axiom that is false in the given interpretation is marked with a line above it):
Naturally, in the last case, the lines intersect only at "the bold points", i.e., in this interpretation, there are five points and ten lines. In particular, the lines $\beta$ and $\gamma$ are both parallel to line $\alpha$.
Sometimes geometric theorems have very similar formulations
but are logically independent statements.
For example:
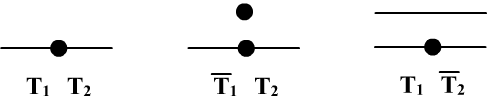
- $(\mathbf{T_1})~~~$ "Every point lies on some line" $~~~~~\forall_x\,\exists_\alpha\,(x\in \alpha)$
- $(\mathbf{T_2})~~~$ "On every line lies some point" $~~~~~\forall_\alpha\,\exists_x\,(x\in \alpha)$
The axioms presented above do not form a complete theory, although in general, plane geometry is complete. To obtain a complete theory, it is necessary to introduce two more relations and their corresponding axioms. The incompleteness of axioms $(\mathbf{A}_1-\mathbf{A}_5)$ follows, in particular, from the existence of finite non-isomorphic models of this theory.
When constructing geometry, one can choose different signatures and axioms. For example, in Tarski's axiomatization, only points are used. Their properties are defined by three basic predicates: equality $x=y$, congruence $(x,y \cong u,v)$ and betweenness $B(x,y,z)$. A line (more precisely, a segment) is defined by two points $\alpha=(x,y)$, and the membership quantifier is defined as $z\in\alpha ~~\Leftrightarrow~~B(x,z,y)$. Semantically, the congruence $(x,y \cong u,v)$ means that the segments $(x,y)$ and $(u,v)$ have equal length. Tarski’s axioms define the properties of these predicates. For example, congruence is "reflexive" $(x,y \cong y,x)$, transitive $(x,y \cong u,v)\,\&\,(x,y \cong s,t)~\to~(u,v \cong s,t)$ and "identical" $(x,y \cong z,z)~\to~x=y$ (a zero-length segment).
A bit of philosophy
Set theory is, in a certain sense, a special kind of theory. Earlier, when discussing formal theories, we referred to sets of objects over which the quantifiers $\forall_x$ and $\exists_x$ ranged. Obviously, when constructing the axiomatic basis of set theory, this approach is not suitable.
Set theory must be built as a pure word game.
There are no true or false statements.
There is no reason to doubt the existence of any objects,
as long as these objects are defined in the form of words. A spoken word already exists.
One may decide that certain words (objects) are inadmissible (do not exist).
But that would be a different (and quite possibly also acceptable) word game.
However, if contradictions arise during the generation of words,
the rules of the game or the initial words (axioms) must, of course, be changed.
For example, consider a signature with a relation $B(x,y)$, whose properties are defined by a single axiom: $\exists_b\,\forall_x\,\bigr[\,B(b,x)~\leftrightarrow~\neg B(x,x)\,\bigr]$. It asserts the existence of some object $b$. Substantively, this theory corresponds to the well-known story of the barber $b$ who shaves all and only those $x$ who do not shave themselves. It is easy to see that this theory is contradictory (when any $x$ equals $b$). Therefore, it is meaningless, and such a barber does not exist - even if his definition is written down. Note that if we remove the phrase " and only those" (replacing $\leftrightarrow$ with $\to$), the theory immediately becomes consistent, and the barber exists and does not shave himself $~~\Rightarrow~\neg B(b,b)$. And with the phrasing "the barber shaves everyone who does not shave himself": $\neg B(x,x)~\to~B(b,x)$, the barber does shave himself $\Rightarrow~~ B(b,b)$.
Most mathematicians are Platonists and believe in the objective existence of mathematical constructions and the a priori truth or falsity of mathematical statements. Like any philosophy, it appears suspicious, but one who doubts the existence of a written word becomes even more of a Platonist than the one who wrote it. Therefore, let's assume that actually infinite sets and the sets of all their subsets "exist", as long as their definitions are written on paper. That said, one must always be prepared for potential complications.
Sets
We will deal with objects $x,y,z,...$, which, in the semantic approach, are interpreted as sets. Nothing exists except sets. All mathematical constructs (numbers, points, etc.) are defined as special types of sets. Sets can be equal $x=y$, and one set can belong to another: $x\in y$, whatever that may mean (in the signature of the theory there are two relations).
Some of the axioms that follow are not independent, and this will be indicated with a prime mark. Nevertheless, the statements they declare are conceptually important. Even though all reasoning about sets can be carried out purely syntactically (a word game), we will simplify our task by using semantics. In our semi-formal reasoning, we will use the concepts of truth and falsehood, as well as standard Boolean and quantifier algebra.
If two sets $x,y$ contain exactly the same elements, then they are equal.
This Axiom of Extensionality in "naive set theory" means that a collection like $\{a,b,a,a,a\}$ is the same as the set $\{a,b\}$. In other words, a set is a collection of pairwise distinguishable elements, each occurring exactly once, and the order of listing elements in a set does not matter.
Since $A\leftrightarrow B$ is equivalent to $(A\to B)\,\&\,(B\to A)$, using the rule of union, the premise of the axiom can be rewritten as: $\forall_z(z\in x~\to~z\in y)~~\&~~\forall_z(z\in y~\to~z\in x)$. The implication under the universal quantifier selects, from "all possible" $z$ only those that belong to $x$ (and then they also belong to $y$), and vice versa. This means that $x,y$ "contain" the same elements. Using the basic signature symbol, we define the relations "$x$ is a subset of $y$" and "$x$ is a proper subset of $y$" as follows: $$ x \subseteq y~~~~~\Leftrightarrow~~~~~\forall_z\,(z\in x ~~\to~~z\in y),~~~~~~~~~~~~~~~~~~~~~~ x\subset y~~~~~\Leftrightarrow~~~~~x\subseteq y~\&~x\neq y. $$ Now the first axiom can be rewritten in the following form: $x\subseteq y~\,\&\,~y\subseteq x~~\to~~x=y$. It is obvious that $x\subseteq x$.
In "naive set theory", for example, $\{a,b\} \subset \{a,b,c\}$. At the same time $a\in \{a,b\}$, but $a\not\subset \{a,b\}$, whereas $\{a\}\subset\{a,b\}$. In other words, the contents inside $\{...\}$ list the elements of the set. Some of them, when enclosed again in curly braces, form a subset. It is important to distinguish between $a$ and $\{a\}$ (a set containing a single element $a$).
A proper subset has the properties of a strict order. For any $x,y,z$ it is: anti-reflexive, transitive, and asymmetric (the last follows from the first two): $$ \neg(x\subset y),~~~~~~~~~~~x\subset z~\to~(z \subset y ~\to~x\subset y),~~~~~~~~~~~~~x\subset y ~\to~\neg(y\subset x). $$
Zermelo-Fraenkel axioms
The following axioms assert the "existence" of certain sets. It is important that each new set is derived from already constructed (previously defined) sets. This approach helps avoid several "paradoxes" found in naive set theory.
Any two sets $x,y$ - and only those two - can be elements of some set $s$.
The set of two elements that exists according to this Pairing Axiom is denoted as $s=\{x,y\}$. Curly braces in this context function like object constructors with an arbitrary number of arguments. In particular, this same axiom "allows" the existence of single-element sets $\{x\}$ (when $x$ and $y$ are equal).
However, the existence of at least one set can also be deduced from the reflexivity of equality: $\forall_x\,(x=x)$ and a generally valid formula $\forall_x P~\to~\exists_x\,P$, giving $\exists_x\,(x=x)$.
The two elements of the set $\{x,y\}$ are unordered: $\{y,x\}$ is the same as $\{x,y\}$. However, using such a pair, one can define an ordered pair $(x,y)$ as follows: $(x,y)~=~\{~\{x\},~\{x,y\}~\}.$ In this case $(y,x)\neq (x,y)$.
For any set $x$, there exists a subset $s$, all elements of which have the property $P$.
The key point in this Axiom of Separation is the use of an already existing set $x$ to construct (i.e., extract from $x$) a new set $s$. In "naive set theory" this axiom looked like this: $\exists_s\,\forall_z\,\bigr[\,P(z) ~\leftrightarrow~z\in s\,\bigr]$. If we substitute $P(z)$ with $z\not\in z$, which is equivalent to $\neg(z\in z)$, we get $\exists_s\,\forall_z\,\bigr[\,z\not\in z ~\leftrightarrow~z\in s\,\bigr]$, and for $z=s$ (since $z$ is arbitrary), this leads to a contradiction - known as the Russell's Paradox. In $\mathbf{ZF_P}$ such a contradiction does not arise.
A subset of elements with a given property is denoted as: $y=\{z\mid z\in x~\&~P(z)\}$.
Naturally, the axiom $\mathbf{ZF_P}$ is an axiom schema, meaning an infinite set of formulas with various predicates $P(z)$.
Now let's prove the following important statement using $(\mathbf{ZF_P})$:
There exists an empty set $s$ that contains no elements.
To prove this, let's substitute $P(z)$ with the formula $z\neq z$. Since this formula is identically false, then according to $\mathbf{ZF_P}$, $z\in s$ must be false, or equivalently, $z\not\in s$ must be true.
The resulting set $s=\varnothing=\{\}=\{z\mid \F\}$ has the property $\forall_z\,(z\not\in\varnothing )$ and is unique. It can be included directly in the signature. The uniqueness of the empty set follows directly from axiom $\mathbf{ZF_=}$: if $\varnothing$ and $\varnothing'$ both contain the same (namely, no) elements, they must be equal. Let’s demonstrate this a bit more formally. The relation $\varnothing \subseteq \varnothing'$, which is equivalent to $\forall_z(z\in \varnothing~\to~z\in \varnothing')$, is true (since the premise is false). Similarly, $\varnothing' \subseteq \varnothing$ is also true. Therefore, by $(\mathbf{ZF_=})$ these sets are equal: $\varnothing = \varnothing'$.
Recall that $\varnothing=\{\}$ and $\{\varnothing\}=\{\{\}\}$ are different sets ("an empty box" and "a box containing an empty box"). The empty set is a subset of any set: $\varnothing\subseteq y$ since the premise in $\forall_z\,(z\in \varnothing ~\to~z\in y)$ is false.
There exists a set $s$ equal to the union of all sets contained in a given set $x$.
Semantically, the Axiom of Union means that if there is, for example, a two-element set $\{\{a\},~\{b,c\}\}$, we can construct a three-element set: $\{a,~b,~c\}$, and so on. Such a set, obtained by "shaking out" the sets that are elements of $x$, is denoted as $\cup x = \{z\mid \exists_w\,(~z\in w\,\&\,~w\in x)\}$. Using this, one can define: $$ x\cup y ~~~~\Leftrightarrow~~~~\cup\{x,y\}~~~~\Leftrightarrow~~~~\{z\mid z\in x \vee z\in y\}. $$ In particular, $\{a\}\cup \{b,c\} ~=~\{a,b,c\}$, and so on.
For any set $x$, there exists a set $s$ consisting of all and only the subsets of $x$.
This is the Axiom of Power Set for a given $x$ and it allows for the construction of the set $s=\{z\mid z\subseteq x\}$. Such a set is denoted as $2^x$.
Note that in all axioms of "existence" of set $s$ the symbol of equivalence $\leftrightarrow$ ("if and only if") is used, rather than implication $\to$ ("if ...then"). Let us clarify this using the last axiom. The formula $z\subseteq x ~\to~z\in s$ means "every subset $z$ of the set $x$ is an element of $s$". But if $z$ is not a subset of $x$, then $z\in s$ can be either true or false. In other words, this formula says that the set $s$ contains all subsets of $x$ and possibly some other elements as well. The reverse implication $z\in s ~\to~z\subseteq x$ states that all elements of $s$ are subsets of $x$, but not necessarily all subsets. Only the combination of these two formulas $(A \to B)\,\&\,(B\to A)$ with $A \leftrightarrow B$ leads to "$s$ consists of all subsets of $x$ and only them". In principle, a weaker version of this axiom (without the "only them" part) can also be used.
The previous six statements declared the existence of finite sets with any number of elements. The following axiom allows the existence of infinite sets.
There exists a set $s$ with an infinite number of elements.
The Axiom of Infinity inductively introduces the concept of actual infinity
as a completed collection $s$.
First, it asserts that the set $s$ contains some arbitrary element
$x$ (for example, $\varnothing$).
Then, that every element $z$ of the set $s$ is a member of at least one element $w$ of the same set $s$.
For example, if $\varnothing$ exists, then $\{\,\varnothing\,\}$,
must also exist, and therefore so must
$\{\,\{\,\{\varnothing\}\,\}\,\}$, and so on - continuing indefinitely.
Every non-empty set $x$ contains an element $z$ that shares no elements with $x$.
The Axiom of Regularity (also called the Axiom of Foundation) can be expressed using the intersection function of sets $x\cap y = \{\,z\mid z\in x~\&~z\in y\,\}$,
in the following form: $x\neq \varnothing ~\to~\exists_z\,(z\in x ~\&~z\cap x=\varnothing)$.
Its meaning is that in any non-empty set $x$, there exists an element $z$ that is
"minimal" with respect to the membership relation $\in$
(i.e., there is no $w$ such that $w\in x$).
In the set $x=\{\{a,b\},~a\}$ such an element is $z=a$. At the same time, $a$ cannot depend on itself (see below).
This axiom also prohibits more subtle recursive relationships. If $x=\{a,\,b\}$, then it must be the case that $(a\not\in b~\vee~b\not\in a)$.
From the axioms of regularity and pairing,
it follows that no set
can be an element of itself: $z\not\in z$.
Proof by contradiction: suppose $z\in z$.
By the axiom of pairing, there exists a set $x=\{z\}$.
This set is non-empty, and therefore, $z\cap x=\varnothing$.
But this is not the case, since $z\in z$ and $z\in x$, i.e., $z$ belongs to the intersection.
This same axiom also implies that there can be no infinite descending chain of nested sets: $ ... \in x_2 \in x_1$, i.e., the number of paired curly braces is always finite.
Let $x$ be a finite set consisting of $n$ non-empty, disjoint sets $w$. It is "obvious" that by taking one element $z$ from each set $w$, one can construct a new set $s$ with $n$ elements. This set will intersect each original set at exactly one element. For an infinite number of sets, however, this method of constructing a new set is not entirely "self-evident" and must be governed by the Axiom of Choice.
Natural numbers as sets
In the Platonic world of mathematical ideas, there is nothing but sets. Any entities that, in naive set theory, were elements of sets but not sets themselves, must now be defined in terms of sets. Thus, all of mathematics is henceforth constructed using only the language of sets. For example, let's define the set of natural numbers $\mathbb{N}=\{0,1,2,...\}$ using von Neumann’s idea.
Let the set $\varnothing$ be equivalent to the number $0$. We then introduce a set with one element: $\{0\}$ or $\{\, \varnothing \,\}$. All other natural numbers are built by the following scheme: if $x\in \mathbb{N}$, then $n(x)=x+1~=~x\cup \{x\}$ also belongs to $\mathbb{N}$: $$ 0:=\varnothing,~~~~~~~1:=\{0\}=\{\, \varnothing \,\},~~~~~~~~~2:=\{0,1\}=\{\, \varnothing,~ \{\, \varnothing \,\} \,\}, ~~~~~~~~ 3:=\{0,1,2\} = \{\, \varnothing,~ \{\, \varnothing \,\},~\{\, \varnothing,~ \{\, \varnothing \,\} \,\} \,\}. $$ Their union forms the set $\mathbb{N}$. Naturally, it is necessary to show that the entities introduced in this way possess the usual arithmetic properties. For example, it is immediately evident that they are linearly ordered, where the order relation is the strict subset relation: $x\lt y~~\Leftrightarrow~~x\subset y$ (the empty set is a subset of any set): $$ 0 ~\lt~1~~~\Leftrightarrow~~~ \varnothing \subset \{\,\varnothing\,\},~~~~~~~~~~~~ 1 ~\lt~2~~~\Leftrightarrow~~~ \{\varnothing\} \subset \{\varnothing,~\{\varnothing\}\},~~~~~~~~~~~~ 0 ~\lt~2~~~\Leftrightarrow~~~ \varnothing \subset \{\varnothing,~\{\varnothing\}\},... $$ A linear order means that for any $x,y$ one of the following holds: $(x\lt y) \vee (y\lt x) \vee (x=y)$. Note that for this particular collection of sets, the linear order also defines the membership relation $x\in y$ (though in general, the membership relation does not satisfy transitivity: $x\in y~\&~y\in z~\to x\in z$).
If we had defined numbers as sets like
$0:=\varnothing,~~1:=\{\varnothing\},~~2:=\{\{\varnothing\} \},~~
~~3:=\{\{\{\varnothing\}\}\}$, then a linear order could not be introduced,
neither via subset inclusion nor via membership ($0\not\in 2$).
Another approach:
$~~~0:=\varnothing,~~1:=\{\varnothing\},~~2:=\{\varnothing,~\{\varnothing\} \},
~~3:=\{\varnothing,~\{\varnothing\},~\{\{\varnothing\}\}\}, ....$,
is linearly ordered by $x\subset y$, but in this representation, it is difficult to express $n+1$ compactly in terms of $n$.
Ordered sets
Relations in and on
