ML: Logic and Probability. Part I

Introduction

The ability to reason logically under uncertainty is an essential component of any intelligent agent. Using probability theory, binary logic can be generalized to probabilistic models, as will be demonstrated in upcoming articles. Before reading, it may be helpful to review the introduction to logic, to which this document is dedicated as a brief refresher.

The theory of Alice and Bob

Alice and Bob live in a house where each has their own bedroom and they share a common living room. They do not receive guests. Only the owner of a bedroom is allowed to be in it, while both housemates can be in the living room. It is known that someone is in the living room, and Alice is in her bedroom. The task is to conclude that Bob is in the living room.

We will write the statements of the theory using logical negation $\bar{A}$ (not $A$), conjunction $A\,\&\,B$ (logical AND), disjunction $A\vee B$ (logical OR) and implication $P\to Q$, which shortens the phrase "if $P$, then $Q$". Recall that if $\T$ is a true statement and $\F$ is a false one, then for any proposition $P$: $$ \left\{ \begin{array}{lcl} \T~\,\&\,P & \equiv & P\\ \F~\&\,P &\equiv & \F \end{array} \right. ~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} \F\,\vee P &\equiv & P\\ \T\,\,\vee P & \equiv & \T \end{array} \right. ~~~~~~~~~~~~~~~ \left\{ \begin{array}{lclcl} \T\,\to \F &\equiv& \F\\ \T\,\to \T &\equiv& \F\,\to P &\equiv& \T, \end{array} \right. $$ where $\T\,\&\,P \equiv P$ when $P\equiv \F$ and $P\equiv \T$ corresponds to $\T\,\&\,\F \equiv \F$ (truth and false equals false) and $\T\,\&\,\T \equiv \T$. Thus, these formulas are a shorthand for the truth tables for the logical binary operations $\&,~\vee,~\to$.

Let $A$ represent the statement: "Alice is in her bedroom", $B$ - "Bob is in his bedroom", and $L$ - "one or both of them are in the living room". The following facts will serve as axioms describing this world:

The initial premises: $L$ (someone is in the living room), $A$ (Alice is in her bedroom) and axiom $\mathbf{A_1}$ allow us to draw the necessary conclusion in three steps: $$ \begin{array}{llclll} 1. & L,~~~~L\to \bar{A}\vee \bar{B} & \Rightarrow & \bar{A}\vee \bar{B} & ~~~~~~~~~~~& L,\mathbf{A_1},~(\text{MP})\\ 2. & \bar{A}\vee \bar{B} & \Leftrightarrow & A \to \bar{B} & & 1,~\text{def}\\ 3. & A,~~~~A \to \bar{B} & \Rightarrow & \bar{B} & & A,2,~(\text{MP}) \end{array} $$ In the first step, we apply the logical inference rule modus ponens (MP): $$ P,~~P\to Q~~~~\Rightarrow~~~~Q. $$ This rule states: "If formula $P$ is true, and from $P$ follows formula $Q$, then $Q$ is also true". Its validity is tied to the property of implication, which is false only for $\T\to \F~~$ ("you cannot derive falsehood $\F $ from truth $\T $"). Thus, if $P~\equiv~\T$ and $P\to Q~\equiv~\T $, i.e. $\T\to Q~\equiv~\T $, then for $Q$ the only possibility is: $Q\equiv~\T $.
In the second step, we rewrite the implication as a disjunction, which is also a rule of inference (obtaining a new formula). Unlike modus ponens, this rule is bidirectional: $~~P\to Q~~~\Rightarrow~~~\bar{P}\vee Q~~$ and $~~\bar{P}\vee Q~~~\Rightarrow~~~P\to Q$.
In the final step, we again use (MP). Thus, through formal symbol manipulation, we arrive at the correct conclusion that $\bar{B}$: "Bob is not in his bedroom". For this conclusion, we only needed the first axiom, but all three axioms are independent and necessary to describe this world.

First-order predicate theories

In informal theories, we use natural language to describe objects and their properties. However, ambiguities inherent to our thinking are inevitable. The formalization of the subject theory means recording all of its statements as formulas using unambiguous symbols. Deriving some statements from others is done according to clear and unambiguous rules. As a result, the syntax of the theory (its form) is separated from its semantics (content), and no "obviousness" can be implicitly introduced. The logical deduction of such a theory can be verified by, for instance, a computer that knows nothing about the meaning of its symbols.

The construction of a formal subject theory begins with its signature, which lists the types of objects, constants, functions, and predicates. The types of objects are defined by sets of entities with which the theory will operate. In arithmetic, this is the set of numbers, while in plane geometry, there are two sets: points $x,y,...\in \mathcal{P}$ and lines $\alpha,\beta,...\in \mathcal{L}$. Some entities may be declared as special constants (for example, $0$ in arithmetic). The signature of the theory may also include functions $f(x)$, $g(x,y)$, $h(x,y,z)$,..., which map some objects to others (for example, $\text{sum}(x,y)$ or simply $x+y$ in arithmetic). Constants, variables, and functions are called terms. An example of a term: $h(0,x,g(x,y))+f(z)$.

An essential and mandatory part of the signature is predicates - logical functions that depend on the objects: $A(x)$, $B(x,y)$,.... and take the values of truth $\T $ or falsehood $\F $. Logical statements such as $A,B,L$, considered in the previous section, are special cases of constant predicates without arguments.
A property is a predicate with one argument $A(x)$. It defines a subset $\{x\,|\,A(x)\}\subseteq\mathcal{X}$ of objects.
A relation is a predicate $R(x,y)$ with two arguments. It is often written in operational form as $(x\, R\, y)$.
In arithmetic, predicates include the equality of numbers $x=y$ and their order $x\lt y$. In everyday knowledge, for example, $\text{Mather}(x,y):$ "someone $x$ is the mother of $y$" or $(x~\text{in}~y):$ "object $x$ is inside object $y$".

After fixing the signature, a set of formulas is written to define the properties of constants, functions, and predicates. These formulas are called subject axioms. In addition to them, there are general logical axioms that apply to any subject theories and rules of inference (methods for deriving new formulas).

Boolean algebra

When writing statements in a theory (axioms and theorems), logical operators are used in addition to signature symbols: negation $\neg A$ or briefly $\bar{A}$ (not $A$, $A$ is false), disjunction $A\vee B$ (either $A$ or $B$ or both are true) and conjunction $A\,\&\,B$ (both $A$ and $B$ are true). Disjunction and conjunction follow the "usual" properties of commutativity and associativity, similar to addition or multiplication. They are also related by the distributive law and De Morgan's rules:

$$ \left\{ \begin{array}{lcl} A\,\&\,(B\vee C) &\leftrightarrow& (A\,\&\,B)\vee (A\,\&\,C)\\ A\vee(B\,\&\, C) &\leftrightarrow& (A\vee B)\,\&\, (A\vee C) \end{array} \right. ~~~~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} \neg(A\,\&\,B) &\leftrightarrow& \neg A\vee \neg B \\ \neg(A\vee B) &\leftrightarrow& \neg A\,\&\, \neg B \end{array} \right. $$ The double-headed arrow $A\leftrightarrow B$ (or equivalently $A\equiv B$) represents the Boolean operation of logical equivalence, which is true only when the values of the arguments are the same. For example, $\T\leftrightarrow \T$ equals $\T,~~$, while $~~\F\leftrightarrow \T$ equals $\F$.
This operation can be expressed through implication, and implication, in turn, can be expressed through disjunction: $$ A\leftrightarrow B ~~~~~\Leftrightarrow ~~~~~(A\to B)\,\&\,(B\to A), ~~~~~~~~~~~~~~~~~~~~~~~~ A\to B ~~~~~\Leftrightarrow ~~~~~\neg A\vee B. $$ The double arrow $\Leftrightarrow$ denotes the interchangeability of one formula with another and vice versa. This is possible because, for any fixed truth values of $A and B$, the formulas on both sides of the $\Leftrightarrow$ have the same truth value, either $\T$ or $\F$. Essentially, the distributive law and De Morgan's rules could also use $\Leftrightarrow$, making them not just formulas but rules of inference (ways to derive new formulas). There are also specific rules for Boolean algebra, such as absorption rules and always true or false formulas: $$ \left\{ \begin{array}{lcl} A\,\&\,A &\leftrightarrow& A\\ A\vee A &\leftrightarrow& A \end{array} \right. ~~~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} A\,\&\,(A\vee B) &\leftrightarrow& A \\ A\vee (A\,\&\,B) &\leftrightarrow& A \end{array} \right. ~~~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} A\,\&\,\neg A &\equiv& \F \\ A\vee \neg A &\equiv& \T \end{array} \right. $$ All of these examples of Boolean algebra identities are tautologies (formulas that are always true), which can be verified using truth tables (by checking all possible truth values $\F,~\T$ for the statements involved).

Implication $A\to B$ is often used in formulas to express verbal constructions like "if $A$, then $B$".
While implication is true for statements like "If Paris is the capital of England, then the Earth is flat" ($\F \to \F$ is true), there is usually a causal relationship between the premise $A$ and the consequence $B$. It’s important to remember that the statement in the implication assumes the truth of the premise. What happens if the premise is false is not specified. For example, "If Masha is left alone, she will be happy", says nothing about what happens if Masha is not left alone.
Similarly, in arithmetic, the formula $(x\lt 2) \to (x\lt 4)$ is true for any $x$. When the premise is true ($x=1$), the consequence is also true. If the premise is false, the consequence can be either true ($x=3$), or false ($x=5$).

Quantifiers

Quantifiers play an important role in constructing formulas in formal theories:

For finite sets $x\in\{a_1,\,...,\,a_n\}$ quantifiers are equivalent to a chain of disjunctions and conjunctions: $$ \exists_x \,P(x)~~~\Leftrightarrow~~~P(a_1)\vee P(a_2)\vee .... \vee P(a_n),~~~~~~~~~~~~~~~ \forall_x \,P(x)~~~\Leftrightarrow~~~P(a_1)\,\&\, P(a_2)\,\&\, .... \,\&\, P(a_n). $$ Indeed, "there exists" means that either $P(a_1)$ is true, or $P(a_2)$ is true, or... (at least one of them). Similarly, for the universal quantifier, all $P(a_i)$ must be true.

For finite sets, both $\exists_x \,P(x)$ and $\forall_x \,P(x)$ can be computed by knowing the truth value of the predicate $P(x)$ for each $x$. For infinite sets, this is not the case. More specifically, if the set is countable and there is an object that satisfies $P(x)$, it will eventually be found in the chain $P(a_1)\vee P(a_2)\vee...$ However, if no such object exists, the "search algorithm" will never stop. Similarly, if the formula $\forall_x\, P(x)$ is true, it cannot be verified by exhaustive checking, though its falsehood can be established by finding an instance where $P(a_i)\equiv 0$.

Quantifiers are analogous to summation signs, and their "index" can be denoted by any variable.
A formula in which all variables are bound by quantifiers is called a closed formula (containing no free variables). For example, if we assume that quantifiers have the highest priority (are applied first), then the formula $\forall_x\,P(x,y)~\to~\exists_y\,Q(x,y)$ is a predicate $F(x,y)$ with two arguments: $ \bigr(\forall_u\,P(u,y)\bigr)~\to~\bigr(\exists_v\,Q(x,v)\bigr). $
Free variables (such as $x and y$ above) are called parameters of the formula, while bound variables ($u and v$) are simply referred to as variables.

Identical quantifiers can be swapped (this also applies to the existential quantifier $\exists$): $$ \forall_x\,\forall_y \,P(x,y) ~~~~~\Leftrightarrow~~~~~ \forall_y\,\forall_x\, P(x,y)~~~~~\Leftrightarrow~~~~~ \forall_{x,y}\, P(x,y). $$ In general, different types of quantifiers cannot be swapped. For example, $\forall_y\, \exists_x \,\text{Mather}(x,y)$ means that for every $y$ there exists a mother $x$. On the other hand, $\exists_x\,\forall_y \, \text{Mather}(x,y)$ means that there exists an $x$ who is the mother of everyone, including herself.

Using Boolean algebra, it is easy to derive various identities for quantifiers. For example, from De Morgan's rules it follows that there is no $x$ such that $P(x)$ is true, equivalently, that for all $P(x)$ is false: $$ \neg\exists_x\,P(x)~~~\Leftrightarrow~~~\forall_x\,\neg P(x), ~~~~~~~~~~~~~~~~~~~ \neg\forall_x\,P(x)~~~\Leftrightarrow~~~\exists_x\,\neg P(x). $$ For any quantifier (where ($\text{K}_x$ represents either $\forall_x$ or $\exists_x$), the rules of scope extension hold, and for "related" operations ($\&$ for $\forall$ and $\vee$ for $\exists$), the rules of combination apply: $$ \left\{ \begin{array}{lcl} \text{K}_x\, P(x)\,\&\, Q~~~&\Leftrightarrow&~~~ \text{K}_x\, \bigr(P(x)\,\&\, Q\bigr)\\ \text{K}_x\, P(x)\vee Q~~~&\Leftrightarrow&~~~ \text{K}_x\, \bigr(P(x)\vee Q\bigr)\\ \end{array} \right. ~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} \forall_{x}\,P(x)~\,\&~\forall_{y}\,Q(y)~~~&\Leftrightarrow&~~~\forall_{x}\,\bigr(P(x)\,\&\,Q(x)\bigr) \\ \exists_{x}\,P(x)\,\vee\,\exists_{y}\,Q(y)~~~&\Leftrightarrow&~~~ \exists_{x}\,\bigr(P(x)\vee Q(x)\bigr) \end{array} \right. $$ In the rules of scope extension, it's important that the formula $Q$ does not depend on the variable $x$ (though it may depend on parameters). Because of this, $Q$ is either $\T$ or $\F$. By considering these two possibilities, the truth of these rules can be easily verified.

◊ Let $x\in \mathbb{Z}=\{0,\pm 1,\pm 2,...\}$ (integers), the addition function $x+y$ and the equality predicate $x=y$ are defined in the usual way. For the formulas below, the first two are true, while the latter two are false: $$ (a)~~~\exists_{x,y}\,[x+y=5],~~~~~~~~~~(b)~~~\forall_x\,\exists_y\,[x+y = 5],~~~~~~~~(c)~~~\forall_{x,y}\,[x+y = 5],~~~~~~~(d)~~~\exists_y\,\forall_x\,[x+y = 5]. $$ For $(a)$, examples include $x=2$ and $y=3$. In $(b)$, for every $x$ there exists $y=5-x$.

◊ For natural numbers $x\in\mathbb{N}=\{0,1,2,...\}$, we can express (define) the relation $x\mid y:$ "number $x$ divides $y$" through the multiplication function $x\cdot y$ and write the following statements: "Some even numbers are divisible by $4$"; "Every number divisible by $4$ is also divisible by $2$": $$ (x\mid y) ~~~\Leftrightarrow~~~\exists_z\,(x=y\cdot z)~~\&~~y\neq 0,~~~~~~~~~~~~ \exists_x\,\bigr[\, (x\mid 2)~\&~(x\mid 4)\,\bigr],~~~~~~~~~~~~ \forall_x\,\bigr[\,(x\mid 4) ~\to~(x\mid 2)\,\bigr]. $$

A formula’s prenex form is its equivalent form in which the action of all quantifiers covers the entire formula. For example, $$ \forall_x\, P(x)\,\&\,\exists_y\,Q(y)~\to~\exists_z\,R(z)~~~~~\Leftrightarrow~~~~~~ \exists_x\, \bar{P}(x)~\vee~ \forall_y\,\bar{Q}(y)~\vee~\exists_z\,R(z) ~~~~~\Leftrightarrow~~~~~~\exists_x\,\forall_y\,\bigr[ P(x)\,\&\,\,Q(y)~\to~R(x)\bigr], $$ where after eliminating the implication, the union rule for $\exists_x,\,\exists_y$ is applied, followed by the expansion rules.

Interpretations of the theory

Interpretation of a formal theory refers to giving the elements of the signature meaningful content (semantics).
For this, specific non-empty sets are defined (consisting of a finite or infinite number of elements). On these sets, constants, functions, and the values of predicates ($\F ,\T $) are determined.

If a signature contains only propositions, then a universally valid formula is called a tautology ($A\vee \neg A$).
If the subformulas of any formula can be designated as propositions in a way that results in a tautology, then the formula is universally valid. For example, $\forall_x\,P(x) \,\vee\, \neg \forall_y\,P(y)$ is a tautology. At the same time, the universally valid formula $\forall_x P(x)\,\to \exists_y\,P(y)$ is not a tautology.

A model of a formula is an interpretation in which the formula is true. If a model exists, the formula is satisfiable.
A model of a theory is an interpretation in which all the axioms and theorems of the theory are true.

◊ Consider a subject theory with two predicates: $x=y$ (equality), $x \prec y$ (order), and one function: $x\circ y$ (whatever it may represent). We take a set of three elements, numbered as follows: $\mathbb{X}=\{0,1,2\}$. On this set, we define two different interpretations:

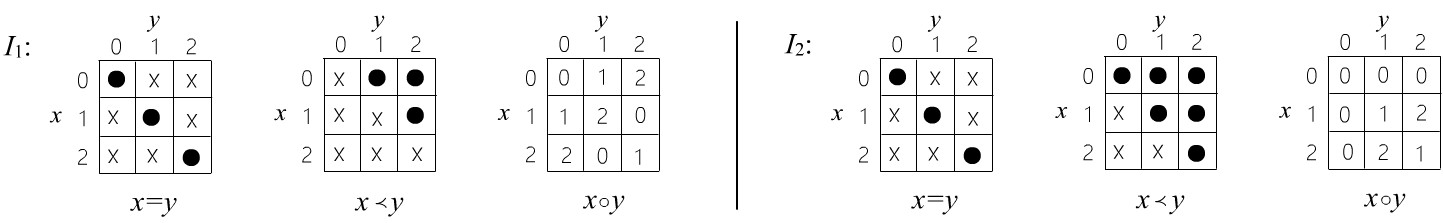
In the tables for the predicates, a dot represents truth, while a cross represents falsehood. For instance, $2=2$ is true, and $2=1$ is false. The predicate $x=y$ is defined the same way in both interpretations, while the other elements of the signature have different values. It is easy to verify that in both signatures, the formula $\forall_{x,y}\,[ (x\circ y) = (y\circ x) ]$ (commutativity) is true. The formula $\forall_x\,\exists_y\, (x\prec y)$ is false in the first interpretation and true in the second. The formula $\exists_x\,\forall_y\,(x\prec y)~\to~\forall_y\,\exists_x\,(x\prec y)$ is true in both interpretations (it is, in fact, a universally valid formula).

Logical consequence

Imagine a set of interpretations $\mathcal{I}$, where the elements are subject-specific sets with interpretations defined on them. Two identical sets, where functions and predicates are defined differently, are distinct elements of the set $\mathcal{I}$. We will assume that any closed formula (without parameters) in a given interpretation is either true or false (for finite sets, this is obvious). Therefore, on the set of interpretations $\mathcal{I}$, there exist truth subsets for each formula (the set of its models).

A formula $Q$ logically follows from formula $P$ if, whenever $P$ is true, $Q$ is also true. In the set of interpretations, the truth domain of $P$ is a subset of the truth domain of $Q$. This consequence is denoted as: $P\vDash Q$, and if $Q$ is universally valid, it is denoted as $\vDash Q$.

The logical deduction $\mathcal{P}\Rightarrow Q$ is the derivation of a new formula $Q$ from formulas $\mathcal{P}$ such that $\mathcal{P}\vDash Q$. For example, in modus ponens: $P,~P\to Q~ \Rightarrow~ Q$ (MP), from the formulas $P$ and $P\to Q$ we deduce $Q$. In this case, $Q$ is at least true in the same interpretations where $P$ and $P\to Q$ are true.

The definitions of logical implication and inference lead to the following useful statement:

if $~~P\Rightarrow Q,~~$ then $~~~\vDash~P\to Q~~$ (the formula is universally valid) and vice versa by (MP).
For example, inference by modus ponens is equivalent to the universally valid formula $(P\,\&\,(P\to Q)) \to Q$, which, in turn, is equivalent to $(P\,\&\,Q)\,\to\,Q$.

Another universally valid formula $P\to (P\vee Q)$ corresponds to the logical inference $P~\Rightarrow~ P\vee Q$ (if $P$ is true, then regardless of the truth value of formula $Q$, $P\vee Q$ will be true).

To the right, you can see a theory with two axioms, $A_1 and A_2$. Their truth domains are bounded by bold lines. From these axioms, three formulas (theorems) $T_1, T_2, and T_3$ follow. This is because the intersection of the truth domains of axioms $A_1$ and $A_2$ (the shaded area) is a subset of the truth domains of all three theorems. Additionally, there is an inference $T_1\Rightarrow T_2$, but neither $T_1$ nor $T_2$ implies (or can derive) $T_3$. To infer theorems $T_1$ and $T_2$ both axioms $A_1$ and $A_2$ are needed. For $T_3$, only axiom $A_2$ is sufficient. The formula $T_4$ is always false in this theory (its negation $\neg T_4$ is logically implied and derivable).

✒ Here are some examples of one-sided inference rules for formulas with quantifiers: $$ \forall_x\,P(x)~~~\Rightarrow~~~ P(x)~~~\Rightarrow~~~ P(t)~~~\Rightarrow~~~ \exists_x\,P(x). $$ The first rule, dropping the universal quantifier $\forall_x\,P(x)~\Rightarrow~ P(x)$, means that if $P(x)$ is true for all $x$, then the formula $P(x)$ will be universally valid (always true) no matter what value of $x$ is substituted. The reverse implication, however, is not generally true. In particular, $P(x)\,\to\,\forall_y\,P(y)$ is not universally valid, for example, for $x\in\{a_1,a_2\}$ where $P(a_1)\equiv\T$, $P(a_2)\equiv\F$ for $x=a_1$. However, $\forall_y\,P(y)~\to~ P(x)$ is a universally valid formula.

The next inference $P(x)~~\Rightarrow~~ P(t)$ means you can substitute any term $t$ (constant, variable, or function) for the variable $x$ in the already derived formula $P(x)$ in place of the parameter $x$. Thus, from the formula $x+y=y+x$ we derive $x+(x+1)=(x+1)+x$ by simultaneously replacing $y$ with $x+1$.

The last one-sided inference $P(t)~\Rightarrow~\exists_x\,P(x)$ means that if $P(t)$ is true for a given term $t$, then this value (at least one) exists. The reverse implication is generally not true, and the formula $\exists_y\,P(y)~\to~P(x)$ is not universally valid (it fails on $P(a_1)\equiv \T$, $P(a_2)\equiv \F$ for $x=a_2$).

If the formula $Q(x)$ is derived directly from the axioms (without using premises) after dropping the universal quantifier $\forall_x\,P(x)~\Rightarrow~ P(x)~\Rightarrow~...~\Rightarrow~Q(x)$, then it holds for all $x$, and you can apply the generalization rule $Q(x)~\Rightarrow~\forall_x\,Q(x)$.

☯ Unfortunately, the concept of a formula's truth on a given interpretation is well-defined only for finite sets. For infinite sets, it is not always possible to "compute" its truth. Moreover, there are formulas that are true on all finite sets but false on infinite ones. For example, in finite linearly ordered sets with the relation $x\preceq y$, there are always largest elements: $\exists_y\forall_x (x\preceq y)$. However, for infinite sets like the natural numbers, this is no longer the case.

Nevertheless, the concept of truth subsets of formulas on the set of interpretations is important for understanding the axiomatic properties of formal theories and can sometimes be useful in practice. For instance, instead of deriving a formula from axioms, an intelligent system may verify its "empirical truth" by checking logical consequence across a large number of interpretations.

Proof by contradiction

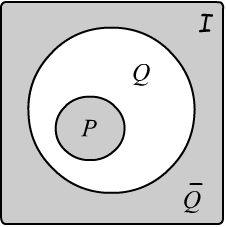The image on the right illustrates a very powerful method called proof by contradiction.
Instead of proving $P \Rightarrow Q$ directly, we assume the negation of $Q$ ("let $Q$ be false..."). If logical reasoning from these assumptions leads to a contradiction $P,\,\neg{Q}~\Rightarrow~\F$, then $P \Rightarrow Q$ must hold. Indeed, if $P \Rightarrow Q$, the truth domain of $P$ is a subset of $Q$ and has no intersection with the truth domain of $\neg Q$. Therefore, the set of formulas $\{P,\,\neg{Q}\}$ or the formula $P\,\&\,\neg{Q}$ is unsatisfiable, i.e., contradictory.

For many statements, a direct proof is either unknown or much longer than a proof by contradiction (especially when reasoning about the existence or non-existence of objects with certain properties).

◊ A classic example is the proof that $\sqrt{2}$ cannot be expressed as $n/m$, where $n,m\in \mathbb{N}^+=\{1,2,...\}$.
Here, $P$ represents the axioms of arithmetic. We aim to prove the formula $Q:~\sqrt{2}\neq n/m$, where $n/m$ is an irreducible fraction.
Assume the negation $\bar{Q}: ~\sqrt{2}=n/m$. Squaring both sides, we get $n^2=2\,m^2$, which implies $n$ is even, i.e., $n=2\,k$.
But then $(2k)^2 = 2m^2$ or $m^2 = 2k^2$, meaning $m$ is also even, which contradicts the irreducibility of the fraction $n/m$.

In predicate logic, proof by contradiction allows us to eliminate quantifiers and reduce logical inference to a simpler procedure, often used in automated theorem proving programs.

Consider the formula $S:~\exists_x\,P(x)$. Suppose we need to prove that it is unsatisfiable. We introduce a new constant $a$ into the theory's signature and write the formula $S':~P(a)$. The formulas $S$ and $S'$ are not equivalent, and in particular, $\exists_x\,P(x)~\to~P(a)$ is not universally valid (its counterexample: $x\in\{a,b\}$, $P(a)\equiv \F$, $P(b)\equiv \T$).
This makes sense because the formula $\exists_x\,P(x)$ does not assert that the existing $x$ is unique, whereas in $P(a)$, the introduced constant exists in a single instance.

However, the following holds "if $S'$ is unsatisfiable, then the formula $S$ is also unsatisfiable."
Indeed, if $P(a)$ is unsatisfiable but $\exists_x\,P(x)$ is satisfiable, there exists a model where $\exists_x\,P(x)$ is true.
This is only possible if there is some $x$ such that $P(x)$ is true, which contradicts the unsatisfiability of the formula $P(a)$.

In general, eliminating quantifiers requires introducing not only constants but also new Skolem functions. For example, the formula $\forall_x\,\exists_y\,P(x,y)$ means that for each $x$, there exists a $y=f(x)$ such that $P(x,f(y))$ is true. As with constants, this transition is not a logical deduction. However, if $P(x,f(y))$ is unsatisfiable, then the formula $\forall_x\,\exists_y\,P(x,y)$ is also unsatisfiable.

Introducing Skolem constants and functions proceeds from left to right (the arrow $\mapsto$ is not implication, but the transition from formula $S$ to formula $S'$): $$ \exists_x\,\forall_{y,z}\,\exists_u\,\forall_v\,\exists_w\,P(x,y,z,u,v,w) ~~~~\mapsto~~~~ \forall_{y,z,v}\,\exists_w\,P(a,y,z,f(x,y),v,w) ~~~~\mapsto~~~~ \forall_{y,z,v}\,P(a,y,z,f(y,z),v,g(y,z,v)), $$ where for the constant $a$ and functions $f$, $g$, symbols distinct from those in the signature must be used. Also, in $\exists_{x,y}\,P(x,y)~~\mapsto~~P(a,b)$ the constants must be different.

◊ Let’s prove the universal validity of the following formula: $\exists_x\,\forall_y\,R(x,y)~\to~\forall_y\,\exists_x\,R(x,y)$ by contradiction, taking its negation: $\neg(A\to B)~~\Leftrightarrow~~ \neg(\neg A\vee B)~~\Leftrightarrow~~ A\,\&\,\neg B$ and introducing Skolem constants $a,b$: $$ \exists_x\,\forall_y\,R(x,y)~\,\&\,~\exists_y\,\forall_x\,\bar{R}(x,y) ~~~~\Leftrightarrow~~~~~ \exists_x\,\forall_y\,R(x,y),~~~~~\exists_y\,\forall_x\,\bar{R}(x,y) ~~~~~\mapsto~~~~~ \forall_y\,R(a,y),~~~~~\forall_x\bar{R}(x,b). $$ Since both formulas must be true for any $x,y$, we can set $y=b$ and $x=a$, yielding a contradiction: $R(a,b),~~\bar{R}(a,b)$.

Calculus and derivability

At the pinnacle of formalized mathematics is the "Word Game". In this game, a fixed alphabet of symbols $\Sigma$ is used to form words. A subset $\mathcal{L}\subseteq \Sigma^{*}$ of all possible words $\Sigma^{*}$ is called a language (these are the "syntactically correct" words). Some words in the language $\mathcal{A} \subset \mathcal{L}$ are declared as axioms. Then, a set of inference rules is fixed, which generate new words from some set of words within $\mathcal{L}$. If from a given set of words $\mathcal{P}\subset \mathcal{L}$ and axioms $\mathcal{A}$, a sequence of words is produced that ends with the word $Q$, then it is said that it is derivable from the set of words: $\mathcal{P} \vdash Q$. If only axioms are required to derive $Q$, it is said that $Q$ is simply derivable: $\vdash Q$. The triplet {language, axioms, inference rules} is called a calculus.
A derivation $\vdash Q$ in a calculus is a purely syntactic procedure, independent of the semantics of the theory such as the truth or falsity of the formulas, (as opposed to the semantics of logical deduction $\mathcal{P}\Rightarrow Q$).

◊ Let the dictionary consist of two symbols $\Sigma=\{a,b\}$, and the set of axioms consists of four words $\mathcal{A}=\{a,~b,~aa,~bb\}$. There are two inference rules: $W~\vdash~ aWa$ and $W~\vdash~ bWb$, where $W$ is any previously derived word. This calculus generates all two-letter palindromes, such as $aba$, $abbba$, $bbaaabbaaabb$, and so on.

A decidable theory is one for which there exists an algorithm that can determine whether a given formula is derivable from the axioms or not. If no such algorithm exists, the theory is called undecidable. The palindrome theory from the example above is obviously decidable.

In some theories, it is possible to list all of its theorems. These theories are called semi-decidable. In such cases, it is possible to confirm that a theorem is derivable in a finite number of steps (by finding it in the enumeration list), but the algorithm may never stop for non-derivable formulas. Unfortunately, many substantial theories are undecidable.

A key role is played by predicate calculus and its special case, propositional calculus. In predicate calculus, the words are formulas composed of symbols $\Sigma=\{\neg~\,\&~\vee~\to~\leftrightarrow~\forall\,~\exists\,~A~f~x~c~(~~)~,\}$. Arbitrary subject variables $x$, $xx$, $xxx$ are abbreviated as $x,~y,~z$, and similarly for predicate $A$, functional $f$, and constant symbols $c$. The language (syntactically correct formulas) is defined inductively: "if $P$ and $Q$ are formulas, then $(P\vee Q)$ is also a formula", and so on.

Unlike subject theories with a given signature, the axioms of predicate calculus are "obviously" universally valid formulas (true under all interpretations). The inference rules are chosen to preserve universal validity. Therefore, all derivable theorems of the calculus are universally valid. For example, the formula $\exists_x\,\forall_y\,A(x,y)~\to~\forall_y\,\exists_x\,A(x,y)$ is a theorem of the calculus, while $\forall_y\,\exists_x\,A(x,y)~\to~\exists_x\,\forall_y\,A(x,y)$ is not (it is not universally valid). The role of $A$ can be played by any predicate or formula of a specific subject theory. The theorems of predicate calculus are a subset of the theorems of any subject theory. The truth domains of the calculus theorems span the entire space of interpretations (unlike the meaningful theorems of a subject theory). For example, $\forall_{x,y}[(x\lt y)\,\to\,\neg(y\lt x)]$ is a theorem in a subject theory (such as arithmetic), while $\forall_{x,y}[(x\lt y)\,\vee\,\neg(x\lt y)]$ is a universally valid theorem of the calculus.

In principle, in predicate calculus, the symbols for derivability $\vdash$ and $\Rightarrow$ are equivalent. When the more general symbol $\vdash$ is used, common in arbitrary calculi, it emphasizes that the derivation process does not involve the truth of formulas, but is simply a "word game". However, in any case, all derivable formulas in predicate calculus are universally valid. The Gödel's completeness theorem states:

if a formula $P$ is universally valid: $\vDash~P$, then it is derivable: $\vdash~P$.
In propositional calculus, this statement is quite obvious. Its theorems are identities of Boolean algebra. Reducing any formula using this algebra to conjunctive normal form: $(P_1\vee P_2\vee...)\,\&\,(Q_1\vee Q_2\vee...)\,\&\,...$ allows one to prove its truth.

◊ Let’s prove that $P\to(\bar{P}\to Q)$ is universally valid. Transitioning from implication to disjunction, we have: $$ P\to(\bar{P}\to Q)~~~\Leftrightarrow~~~\bar{P}\vee (P\vee Q)~~~\Leftrightarrow~~~(\bar{P}\vee P)\vee Q~~~\Leftrightarrow~~~\T\vee Q ~~~\Leftrightarrow~~~\T. $$ Moving in reverse, from the "axioms" $\bar{P}\vee P$, $~~~\T\vee P$, and rules $P~\Rightarrow~P\vee Q$, $P\vee Q~\Rightarrow~Q\vee P$ etc., one can derive the original formula.

The formulation of independent axioms and inference rules is always of interest. For predicate calculus, for example, one can select the following words: $$ \begin{array}{lcl} P~\to~(Q\to P),\\ (P~\to~(Q\to R))~\to~((P\to Q)\to(P\to R)),\\ (\neg Q\to \neg P) ~\to~((\neg Q\to P)\to Q), \end{array} ~~~~~~~~~~~~~~~~~~~ \begin{array}{lcl} \forall_x\,A(x)~\to~A(t),\\ \forall_x\,(P\to Q(x))~\to~(P\to\forall_x\,Q(x))\\ ~\\ \end{array}, $$ where $P,Q,R$ are any previously derived words, and in the last axiom, $P$ does not contain $x$. This infinite set of axioms is called an axiom schema. For inference rules, it is sufficient to use modus pones and the generalization rule: $$ P,~~P\to Q~~~~~\vdash~~~~~Q,~~~~~~~~~~~~~~~~~~~~~~P(x)~~~\vdash~~~\forall_x\,P(x). $$ These axioms and rules allow the derivation of all strings that are universally valid formulas of predicate calculus.

Consistency and independence of axioms

We define a theory as any finite or infinite set $\mathcal{T}$ of closed, syntactically correct formulas.
The derivation in a theory $\mathcal{T}$ of a formula $Q$ (from the formulas of $\mathcal{T}$ and any universally valid formulas) is denoted as $\mathcal{T}\vdash Q$.
In general, $Q$ may not be universally valid: $\not\vDash Q$, but it logically follows from the theory $\mathcal{T}\vDash Q$ (the intersection of the truth domains of the formulas in $\mathcal{T}$ is a subset of the truth domain of $Q$). Some formulas $\mathcal{A}\subseteq \mathcal{T}$ can be called axioms. The axioms of any well-respected theory should be consistent, independent, and, if possible, complete.

✒ A theory is consistent if its axioms $A_1$, $A_2,...$ intersect in the set of interpretations $\mathcal{I}$, i.e., ) (if there is at least one interpretation $=$ a model, where the axioms are simultaneously true (shown on the right as point $M$). In a consistent theory $\mathcal{T}$, it is impossible to derive both a statement $P$ and its negation $\bar{P}$. Indeed, if $P$ logically follows from the axioms, then the intersection of the truth domains of the axioms (if it exists) must be a subset of $P$ and cannot simultaneously be a subset of $\bar{P}$, (and vice versa, as illustrated).

In a contradictory theory $\mathcal{T}$, there exists a $P$ such that $\mathcal{T} \vdash P$ and $\mathcal{T} \vdash \bar{P}$. In such a theory, any statement can be derived, rendering it essentially useless. Indeed, from $P,\,\bar{P}$ and the tautology $P\to(\bar{P}\to Q)$, using modus ponens twice, we can derive $Q$ (any arbitrary formula).

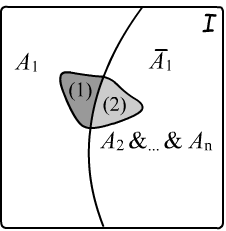✒ Independence means that no axiom can be derived from the others.
Specifically, the truth domains of such axioms do not fully contain other axioms. To prove the independence of axiom $A_1$ from the axioms $A_2,A_3,...$, one must construct an interpretation in which all $A_2,A_3,...$ are true while $A_1$ is false. This shows that the truth domain of $A_1$ is not a subset of the intersection of the truth domains of $A_2,A_3,...$.

If a theory is consistent and its axioms $A_1,...,A_n$ are independent, then a new theory, in which one axiom is replaced by its negation, is also consistent. On the right, the shaded region represents the truth domain of the intersection of axioms $A_2,...,A_n$. The truth domain boundary of axiom $A_1$ divides this region into two parts. The first part $(1)$ contains models of the original theory, while the second part $(2)$ contains models of the new theory, where $A_1\mapsto \bar{A}_1$.

The "more" models a theory has, the "weaker" the system of axioms tends to be. Indeed, when the intersection of the truth domains of the axioms is "large", there are potentially fewer formulas (theorems) whose truth domains are subsets of this region and which can be derived in that theory.

Completeness of the theory

A subject theory $\mathcal{T}$ is complete if it satisfies the following conditions:

1) It is consistent
2) Any closed formula $P$ is either derivable: $\mathcal{T}\vdash P$, or its negation is derivable: $\mathcal{T}\vdash \bar{P}$.
Completeness is a rather non-trivial property of a formal theory, and it's more surprising when complete theories exist rather than incomplete ones.

The illustration shows an example of an incomplete theory, where formulas $P$ and $Q$ intersect with the shaded area representing the intersection of the truth of the axioms (the set of models of the theory). These formulas do not logically follow from the axioms, and thus cannot be derived or refuted. If we add them to the axioms, the theory would have fewer models (represented by the dark gray area). However, if there is an infinite set of similar formulas, adding them may not lead to a complete theory (non-completable incompleteness).

A specific informal subject theory typically deals with a defined set, where functions and predicates of the signature are fixed (the model of the theory). For example, in arithmetic, this infinite set is the natural numbers $\mathbb{N}=\{\,0,\,1,\,2,\,...\,\}$. On it the equality predicate $x=y$ and the functions of addition $x+y$ and multiplication $x\cdot y$ are defined in the "usual way". All these form the interpretation $I_{\mathbb{N}}$, represented as a bold point in the above diagram (located in the truth domain of arithmetic axioms). It is natural to assume that there are formulas that are true in $I_{\mathbb{N}}$, but undecidable (as shown above with formula $P$).
This is the essence of Gödel's incompleteness theorem for arithmetic with the Peano axioms (PA).

◈ A remarkable consequence of the completeness theorem of predicate calculus (if $\vDash P$, then $\vdash P$) is the equivalence of logical consequence and derivability in any theory $\mathcal{T}$:

If $~~~\mathcal{T}\vDash~P,~~~$, then $~~~\mathcal{T} \vdash~P~~~$ and vice versa.
Indeed, let the intersection of the truth domains of the formulas in $\mathcal{T}$ be a subset of the truth domain of $P$.
By the definition of implication, the formula $\mathcal{T} \to P$ is a tautology: $\mathcal{T}\vDash Q~~\Rightarrow~~\vDash \mathcal{T}\to Q~~$ (where $\mathcal{T}$ can be understood as the conjunction of all formulas in $\mathcal{T}$). Therefore, by the completeness theorem of predicate calculus, it is derivable from general logical axioms (tautologies): $\vdash \mathcal{T} \to P$. Consequently, by the modus ponens rule, we obtain $\mathcal{T},~\mathcal{T} \to P ~\vdash~ P$ or (as usual, omitting the universally valid formula) $\mathcal{T}\vdash P$. The reverse implication is obvious, based on the construction of inference rules that preserve the property of logical consequence.

◊ A simple example of an incomplete theory is the theory of equivalence, where the signature contains a relation $x\sim y$, that satisfies the axioms of reflexivity, symmetry, and transitivity: $$ \forall_x\,(x\sim x),~~~~~~~~~~~~~\forall_{x,y}\,\bigr[(x\sim y)~\to~(y\sim x)\bigr],~~~~~~~~~~~~\forall_{x,y,z}\,\bigr[(x\sim y)\,\&\,(y\sim z)~\to~(x\sim z)\bigr]. $$ In this theory, the formula $T:~\forall_{x,y}\,(x\sim y)$ is not derivable because it is false for any set with two or more elements, where $x\sim y$ is "regular" equality (the axioms are valid in these interpretations). Meanwhile, its negation $\bar{T}:~\exists_{x,y}\,\neg(x\sim y)$ is false in a one-element set $\mathbb{M}=\{a \}$ with $(a\sim a)\equiv \T$ (all axioms are valid).

The relation of equality $x=y$ satisfies the same axioms as the equivalence relation $x\sim y$. In addition, an infinite set of formulas (axiom schemes) asserts that if the arguments of functions or predicates in the signature are equal, then their values must also be equal. For instance, if the signature includes a function $f(x,y)$ and a predicate $P(x)$, then the following axioms are added: $$ \forall_{x_1,y_1,x_2,y_2}\,\bigr[(x_1=x_2)\,\&\,(y_1=y_2)~\to~f(x_1,y_1)=f(x_2,y_2)\bigr], ~~~~~~~ \forall_{x_1,x_2}\,\bigr[(x_1=x_2)~~\to~~ (P(x_1) \leftrightarrow P(x_2))\bigr]. $$ A theory whose signature includes equality is called a normal theory. In such theories, equality axioms are not repeated but are implied.

◊ A simple example of a complete theory is one with an "empty" signature, where only equality $x=y$ is present, and the axioms are complemented by the formula $\forall_{x,y}\,(x=y)$. The only model of this theory is a one-element set $\{a\}$ with $a=a$ being $\T$. Any formula either includes this model (the formula is derivable) or does not (the formula is not derivable).

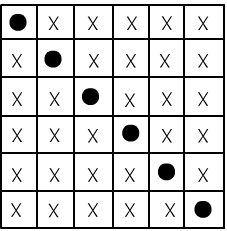
Axiomatic analysis of Alice and Bob

Let's return to the theory about Alice and Bob and prove the consistency and independence of its axioms. The signature of this theory includes only statements (constant predicates) $A,B,L$. To prove consistency, it's enough to provide an example of values for the statements where all the axioms hold true. In normal form these axioms are as follows: $$ (\mathbf{A_1}):~~~~\bar{L}\vee \bar{A}\vee \bar{B},~~~~~~~~~~~~~~(\mathbf{A_2}):~~~~~L\vee A,~~~~~~~~~~~~~(\mathbf{A_3}):~~~~~L\vee B. $$ It is easy to see that for $A=B=\T $ and $L=\F $, they are true ($\T \vee Q \equiv \T $).

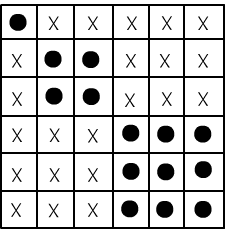
To demonstrate the independence of the axioms, we need to construct an interpretation where all axioms hold except for one. In this simple world, we can describe all possible interpretations in a tabular form. Each element of the table assigns the logical statements $A,B, and L$ either true $\T $ or false $\F $:

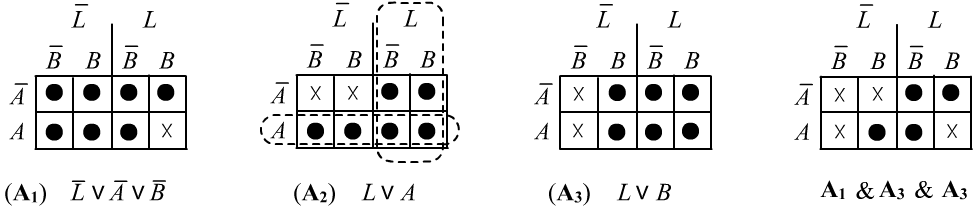
The dots in the tables mark truth ($\T $). Their combination forms the truth set of the formula. In the remaining interpretations (marked with a cross), the formula is false ($\F $). The first axiom is false in the only model where $A=B=L=\T $ (the bottom-right corner of the first table with the cross). In this same model, the second and third axioms are true. Therefore, $A_1$ cannot be derived from $A_2$ and $A_3$. Similarly, it is easy to find interpretations that demonstrate the independence of $A_2$ from $A_1 and A_3$, and $A_3$ from $A_1 and A_2$. Since the statements are connected by disjunctions in normal form, the truth sets are simply the union of the truth sets of the statements (in the second table, the truth of $L$ and $A$ is highlighted with dotted lines).

In the final table, the truth set of the conjunction of all three axioms is shown, which corresponds to the semantics of our problem. Notice that in the story of Alice and Bob, there is an obvious relationship: $L \leftrightarrow \bar{A}\vee \bar{B}$, and satisfying this determines the truth set of the problem. To derive this formula from left to right, $L\Rightarrow \bar{A}\vee \bar{B}$, the first axiom is needed, and to derive it in the opposite direction, $\bar{A}\vee \bar{B} \Rightarrow L$, the remaining two axioms are needed: $$ L,~\mathbf{A_1}~\Rightarrow~\bar{A}\vee\bar{B},~~~~~~~~~~~~~~~~~~~\bar{A}\vee\bar{B},~\mathbf{A_2},~\mathbf{A_3},~\Rightarrow~L. $$

Let’s look at how the derivation of the statement $\bar{B}$ from the beginning of the document appears in terms of interpretation sets:

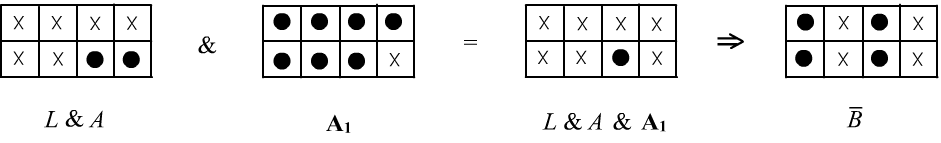
In the first table, the truth set of the initial premises $L and A$ is shown. The second table represents axiom $\mathbf{A_1}$, and the third table shows their intersection using logical AND. This truth set (a single point) is a subset of the truth set of the statement $\bar{B}$. Therefore, it logically follows from the premises and axiom $\mathbf{A_1}$, as demonstrated by the corresponding derivation.

Model theory

Let’s recall that a theory $\mathcal{T}$ is any set of closed formulas. A theory is consistent if there exists an interpretation (model $M$) in which all formulas of $\mathcal{T}$ are true. This is denoted as: $M\vDash \mathcal{T}$.

An elementary theory $\text{Th}(M)$ of a model $M$ is defined as the set of all formulas that are true in $M$. In general, a theory $\mathcal{T}$ with a model $M\vDash \mathcal{T}$ may contain "fewer" formulas than the elementary theory: $\mathcal{T} \subseteq \text{Th}(M)$.

All formulas that follow (and can be derived) from a given theory $\mathcal{T}$ are denoted as $[\mathcal{T}]$. For example, you can take the axioms of the theory as $\mathcal{T}$. Then the set $[\mathcal{T}]$ contains both the axioms and all the theorems derivable from them.

◈ For any model $M$, the theory $\text{Th}(M)$ is complete.

$\triangleleft$ Indeed, $\text{Th}(M)$ is consistent because it has a model. Any formula $P$ in the model $M$ is either true: $M\vDash P$ or false: $M\vDash \neg P$, hence either $P\in \text{Th}(M)$, or $\neg P\in \text{Th}(M)$. $\square$

◈ If a theory $\mathcal{T}$ is complete and $M$ is its model: $M\vDash \mathcal{T}$, then $[\mathcal{T}]=\text{Th}(M)$ and vice versa

$\triangleleft$ Proof by contradiction. Suppose $P\in \text{Th}(M)$ and $\mathcal{T}\not\vdash P$ (i.e., the sets $[\mathcal{T}]$ and $\text{Th}(M)$ do not coincide). Then, due to completeness, $\mathcal{T}\vdash \neg P$. Therefore, $M\vDash \neg P$ and $M\not \vDash P$, which contradicts $P\in \text{Th}(M)$. The reverse follows from the previous assertion. $\square$

Let the objects of the theory belong to a single set. Interpretations $M$ and $N$ are called isomorphic: $M\simeq N$, if between all elements $m\in M$ and $n\in N$ there is a one-to-one correspondence: $n=\alpha(m)$, $m=\alpha^{-1}(n)$ and for all constants $c_N=\alpha(c_M)$, all predicates $A_M(m_1,m_2,...) \leftrightarrow A_N(\alpha(m_1),\alpha(m_2),...)$, and functions $\alpha\bigr(f_M(m_1,m_2,...)\bigr)=f_N(\alpha(m_1),\alpha(m_2),...)$. In other words, in isomorphic interpretations, all elements of the signature are defined identically up to renaming the elements of the sets. For finite sets, the number of elements in $M$ and $N$ must be the same. For infinite sets, the situation can be more complex:

◊ Consider a signature with a function $f(x,y)$ and a constant $c$. Define two interpretations. The first interpretation $M$ is the set of real numbers $\mathbb{R}$, with the function being ordinary addition $f(x,y)=x+y$ and $c=0$. The second interpretation $N$ is the set of non-negative real numbers $\mathbb{R}^+ \ge 0$, with the function $f(x,y)=x\cdot y$, and the constant $c=1$. It is easy to see that $M\simeq N$ with the correspondence: $n=e^{m}$.

Isomorphism $M\simeq N$ possesses the properties of equivalence (reflexive, symmetric, and transitive), and all isomorphic interpretations can be considered "the same".

Models $M$ and $N$ are called elementarily equivalent: $M\leftrightarrow N$, if $\text{Th}(M)=\text{Th}(N)$, meaning the same formulas are true in both. Isomorphic models are elementarily equivalent: $M\simeq N~~\Rightarrow~~M\leftrightarrow N$, but not necessarily vice versa.

◈ If all models of a theory $\mathcal{T}$ are elementarily equivalent, then $\mathcal{T}$ is a complete theory, and vice versa.

$\triangleleft$ Proof by contradiction. Suppose $\mathcal{T}$ is incomplete. Then there exists a formula $P$ for which $\mathcal{T}\vDash P$ and $\mathcal{T}\vDash \neg P$. Then both theories ${\mathcal{T},~P}$ and ${\mathcal{T},~\neg P}$ are satisfiable, meaning they have non-elementarily equivalent models (the theories are different).
However, these models would also be models of $\mathcal{T}$, contradicting the premise. $\square$