ML: Logic and Probability. Part II
Introduction
Formal logic is a special sase of probability theory. This document is a direct continuation of the introduction to logic and formal theories. Now, we will discuss how, using probability theory, we can generalize binary logic to the case of probabilistic models.
Inference in probability theory
We will first limit ourselves to logical theories whose signature contains only propositions. We will interpret them as events. It's important to note that, unlike many-valued or fuzzy logic, in the probabilistic logic discussed here, the law of the excluded middle holds. This means that any proposition is considered either true or false (the event either happens or it doesn’t). However, sometimes we can only specify the probability of a certain outcome.
In probability theory, it is convenient to denote an event as $A$ with capital letters, and its possible "outcomes" as $\{a,\bar{a}\}$ (happened, didn't happen) with lowercase letters. Such an agreement allows us to treat events and random variables, which may take on more than two values, uniformly. It’s important to distinguish between notations where $P(A)$ refers to the probability of the event occurring and $P(\bar{A})=1-P(A)$ refers to it not occurring, from those in which $P(A)$ is a vector with components $\{P(a),P(\bar{a})\}$, and conditional $P(A\to B)$ or joint $P(A,B)$ probabilities are represented as 2x2 matrices. In this case, the expression $P(\bar{A})=1-P(A)$ refers to two formulas $P(\bar{a})=1-P(a)$ and $P(a)=1-P(\bar{a})$, since for events we assume $\bar{\bar{a}}=a$.
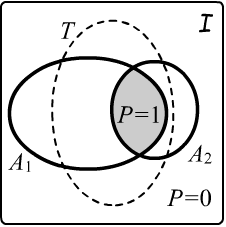 We assign a "metric" to the set of interpretations,
associating a certain probability with each interpretation.
The probability of any formula is the sum of the probabilities of the interpretations where it is true.
Additionally, we assume that the total probability of the interpretations
that satisfy a given formal theory (all its models) equals one.
The probabilities of other interpretations in this theory are zero.
We assign a "metric" to the set of interpretations,
associating a certain probability with each interpretation.
The probability of any formula is the sum of the probabilities of the interpretations where it is true.
Additionally, we assume that the total probability of the interpretations
that satisfy a given formal theory (all its models) equals one.
The probabilities of other interpretations in this theory are zero.
In the figure on the right, the shaded area (the intersection of the truth regions of the axioms $A_1,A_2$) contains interpretations whose combined probabilities sum to one. Interpretations outside the shaded regions have zero probability. As a result, each axiom and theorem derived from them in logic has a probability of one: $P(A_1)=P(A_2)=P(T)=1$. Therefore, to determine if a statement is true in a given theory, it is necessary to find its probability.
Rules of inference
Recall that the probability of event $B$ given that event $A$ has occurred is denoted in a logical manner as $P(A\to B)$, instead of the more common $P(B\,|\,A)$. The joint probability of two events occurring is denoted as $P(A\,\&\,B)$ or simply $P(A,\,B)$. Let’s explore several examples of standard logical inferences in terms of probability theory.
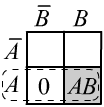 ✒ In logic, the implication $A\to B$ can be replaced by the disjunction $\bar{A}\vee B$ and vice versa.
✒ In logic, the implication $A\to B$ can be replaced by the disjunction $\bar{A}\vee B$ and vice versa.
In probability theory, the following equality
holds: $P(A)\,(1-P(A\to B)) = 1-P(\bar{A}\vee B)$.
Thus, for any $A=\{a,\bar{a}\}$ and $B=\{b,\bar{b}\}$ with $P(A)\gt 0$
the following inference is valid:
$$
P(A\to B) = 1 ~~~~~~~~~~~~~~\Leftrightarrow~~~~~~~~~~~~~P(\bar{A}\vee B) = 1.
$$
Additionally, due to the definition of conditional probability, we have $P(A,B)=P(A)$,
which directly leads to $P(A,\bar{B})=0$, as shown in the figure on the right.
This means that the remaining cells (interpretations) sum to a total probability of one,
which corresponds to $\bar{A}\vee B$, i.e., the union of the first row ($\bar{A}$) and the second column ($B$).
✒
 Similarly, the law of contraposition:
$
A\to B~~\Rightarrow~~\bar{B}\to \bar{A}
$
in probability theory is expressed as:
$$
P(A\to B) = 1~~~~~~~~~~~~~\Leftrightarrow~~~~~~~~~~~P(\bar{B}\to \bar{A}) = 1.
$$
To prove this, you can use the previous rule or get
$P(\bar{B}\to\bar{A})=1$ by contradiction, showing that $P(\bar{B}\to A)=0$:
$$
P(\bar{B})\,P(\bar{B}\to A) = P(A,\bar{B}) = P(A)\,P(A \to \bar{B}) = 0,
$$
where $P(A \to \bar{B})=0$ by the law of total probability derived from $P(A \to B)=1$.
Since in both logic and probability theory for events $\bar{\bar{A}}=A$ and $\bar{\bar{B}}=B$,
this inference is bidirectional. Another way to prove this is by using the fact
that if $P(A\to B)=1$ in the sample space, then
$A\subseteq B$, from which it is clear that $\bar{B}\subseteq \bar{A}$.
Similarly, the law of contraposition:
$
A\to B~~\Rightarrow~~\bar{B}\to \bar{A}
$
in probability theory is expressed as:
$$
P(A\to B) = 1~~~~~~~~~~~~~\Leftrightarrow~~~~~~~~~~~P(\bar{B}\to \bar{A}) = 1.
$$
To prove this, you can use the previous rule or get
$P(\bar{B}\to\bar{A})=1$ by contradiction, showing that $P(\bar{B}\to A)=0$:
$$
P(\bar{B})\,P(\bar{B}\to A) = P(A,\bar{B}) = P(A)\,P(A \to \bar{B}) = 0,
$$
where $P(A \to \bar{B})=0$ by the law of total probability derived from $P(A \to B)=1$.
Since in both logic and probability theory for events $\bar{\bar{A}}=A$ and $\bar{\bar{B}}=B$,
this inference is bidirectional. Another way to prove this is by using the fact
that if $P(A\to B)=1$ in the sample space, then
$A\subseteq B$, from which it is clear that $\bar{B}\subseteq \bar{A}$.
Thanks to this rule, if it is known that for specific values
$P(a\to \bar{b})=1$, then $P(\bar{a}\to b)=1$.
Additionally, according to the law of total probability, the remaining values are zero: $P(a\to b)=P(\bar{a}\to \bar{b})=0$.
Thus, a conditional probability of one fixes the conditional probabilities for all other values.
 ✒ Another bidirectional inference, $C\to A,~C\to B~~~~\Leftrightarrow~~~~C\to A\,\&\,B~~$, has the form:
$$
P(C\to A) = P(C\to B) = 1 ~~~~~~~~~~~~~~\Leftrightarrow~~~~~~~~~~~~~P(C \to A,B) = 1.
$$
This can be proven right-to-left using the formula for total probability. Since $P(C\to A,B)=1$, we have
$$
P(A,B,C) = P(C)= P(A,B,C) + P(A,\bar{B},C) + P(\bar{A},B,C) + P(\bar{A},\bar{B},C).
$$
As all probabilities are non-negative, it follows that
$P(A,\bar{B},C)=P(\bar{A},B,C)=P(\bar{A},\bar{B},C)=0$ or $P(\bar{B},C)=P(\bar{A},C)=0$.
Thus, $P(C)=P(A,C)+P(\bar{A},C)=P(A,C)$, and similarly, $P(C)=P(B,C)$.
✒ Another bidirectional inference, $C\to A,~C\to B~~~~\Leftrightarrow~~~~C\to A\,\&\,B~~$, has the form:
$$
P(C\to A) = P(C\to B) = 1 ~~~~~~~~~~~~~~\Leftrightarrow~~~~~~~~~~~~~P(C \to A,B) = 1.
$$
This can be proven right-to-left using the formula for total probability. Since $P(C\to A,B)=1$, we have
$$
P(A,B,C) = P(C)= P(A,B,C) + P(A,\bar{B},C) + P(\bar{A},B,C) + P(\bar{A},\bar{B},C).
$$
As all probabilities are non-negative, it follows that
$P(A,\bar{B},C)=P(\bar{A},B,C)=P(\bar{A},\bar{B},C)=0$ or $P(\bar{B},C)=P(\bar{A},C)=0$.
Thus, $P(C)=P(A,C)+P(\bar{A},C)=P(A,C)$, and similarly, $P(C)=P(B,C)$.
The inference from left to right follows similarly from $P(A,C)=P(C)$ and $P(B,C)=P(C)$, by applying the total probability formula to both sides.
 ✒ The one-way inference of modus ponens $A,~A\to B~~\Rightarrow~B$:
$$
P(A)=P(A\to B)=1~~~~~~~~~~~\Rightarrow~~~~~~~~~~~P(B)=1
$$
can be proven using the total probability formula: $P(B)=P(A,B)+P(\bar{A},B)=1 + P(\bar{A},B)\le 1$,
taking into account that the premises provide $P(A,B)=1$. Since probabilities are non-negative, we conclude that $P(B)=1$.
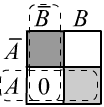
The graphical proof is shown in the figure. Given $P(A,B)=P(A)=1$, we have $P(A,\bar{B})=0$ and $P(A,B)=1$.
That's why there are zeros in the top row. The non-zero truth domain is a subset of the truth
$P(B)=1$ (second column).
✒ The one-way inference of modus ponens $A,~A\to B~~\Rightarrow~B$:
$$
P(A)=P(A\to B)=1~~~~~~~~~~~\Rightarrow~~~~~~~~~~~P(B)=1
$$
can be proven using the total probability formula: $P(B)=P(A,B)+P(\bar{A},B)=1 + P(\bar{A},B)\le 1$,
taking into account that the premises provide $P(A,B)=1$. Since probabilities are non-negative, we conclude that $P(B)=1$.
The graphical proof is shown in the figure. Given $P(A,B)=P(A)=1$, we have $P(A,\bar{B})=0$ and $P(A,B)=1$.
That's why there are zeros in the top row. The non-zero truth domain is a subset of the truth
$P(B)=1$ (second column).
✒ Besides modus ponens,
formal logic has many other non-trivial ways of deriving
new true formulas.
A very powerful method, widely used in automated reasoning, is
the resolution rule:
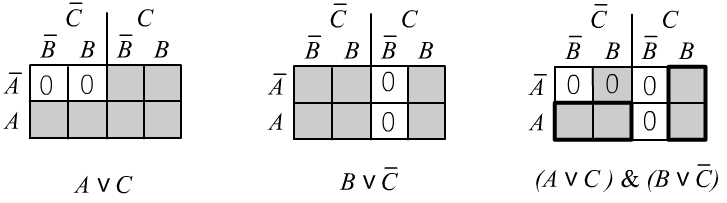
$$
A\vee C,~~~B\vee\bar{C}~~~~\Rightarrow~~~~A\vee B
$$
(The premises are true, so if $C\equiv \F $, then $A\equiv \T $,
if $C\equiv \T $, then $B\equiv \T $, and in any case $A\vee B\equiv \T $).
Let’s prove this rule by listing interpretations:
It is also worth verifying the correctness of the inference using the property of transitivity of implication: $ A\to B,~B\to C~~\Rightarrow~~A\to C, $ which corresponds to the probabilities: $$ P(A\to B) = P(B\to C) = 1 ~~~~~~~\Rightarrow~~~~~~~~P(A\to C) = 1. $$ In fact, this result also follows directly from the resolution method.
Alice and Bob revisited
✒ Let’s consider probabilistic logical inference in the theory about Alice and Bob. We will express the axioms $(\mathbf{A_1})-(\mathbf{A_3})$ as follows: $$ P(l\to \bar{a}\vee \bar{b}) ~=~ P(\bar{l}\to a) ~=~ P(\bar{l}\to b) ~=~ 1. $$ Note that in logic, axioms like $\bar{L}\to A$ are true for any values of the statements $L,\,A$ in the set of true interpretations for this theory. In probability theory, they must be used with “semantically correct” specific values, as shown above. Otherwise, the relation $P(\bar{L}\to A)=1$ would lead to a contradiction: $P(\bar{L}\to a)=P(\bar{L}\to \bar{a})=1$ for both $A=a$ and $A=\bar{a}$.
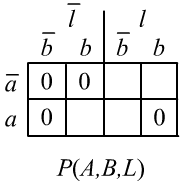 Using the implication reversal rule, we can immediately derive:
$$
P( a,b \to \bar{l}) ~=~ P(\bar{a}\to l) ~=~ P(\bar{b}\to l) ~=~ 1,
$$
and from the total probability formula, we get (capital letters $A$, $B$ represent any value):
$$
P(a,b,l)~=~P(\bar{a},B,\bar{l})~=~P(A,\bar{b},\bar{l}) ~=~ 0.
$$
Thus, the axioms set the joint probabilities $P(A,B,L)$ to zero,
as shown in the table to the right (probabilities of interpretations), but they do not provide values for the “non-logical probabilities”
in the empty cells. All we know is that their total probability equals one.
Using the implication reversal rule, we can immediately derive:
$$
P( a,b \to \bar{l}) ~=~ P(\bar{a}\to l) ~=~ P(\bar{b}\to l) ~=~ 1,
$$
and from the total probability formula, we get (capital letters $A$, $B$ represent any value):
$$
P(a,b,l)~=~P(\bar{a},B,\bar{l})~=~P(A,\bar{b},\bar{l}) ~=~ 0.
$$
Thus, the axioms set the joint probabilities $P(A,B,L)$ to zero,
as shown in the table to the right (probabilities of interpretations), but they do not provide values for the “non-logical probabilities”
in the empty cells. All we know is that their total probability equals one.
However, logical inferences can be made from premises, just as in Boolean logic. For example, let’s prove that from $A=a$ and $L=l$, it follows that $B=\bar{b}$. We will use the method of contradiction. If $P(a,l\to \bar{b})=1$, then by the total probability formula, we must have $P(a,l\to b)=0$. Indeed: $$ P(a,l \to b) = \frac{P(a,b,l)}{P(a,l)} = 0. $$
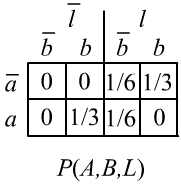 ✒ Probability theory is more flexible than Boolean logic
because it allows us to express non-binary probabilities as well.
For example, suppose it is known that Alice is more often in the living room than Bob,
and the probability of finding anyone in the living room is $1/3$:
$$
P(l\to \bar{a}, b) = \frac{1}{2},~~~~~~~~
P(l\to a, \bar{b})=\frac{1}{4},~~~~~~~~
P(l\to \bar{a}, \bar{b})=\frac{1}{4},~~~~~~~~~~P(\bar{l})=\frac{1}{3}.
$$
Together with the axioms, this information is sufficient to answer any question.
The corresponding joint probabilities are shown in the table to the right.
✒ Probability theory is more flexible than Boolean logic
because it allows us to express non-binary probabilities as well.
For example, suppose it is known that Alice is more often in the living room than Bob,
and the probability of finding anyone in the living room is $1/3$:
$$
P(l\to \bar{a}, b) = \frac{1}{2},~~~~~~~~
P(l\to a, \bar{b})=\frac{1}{4},~~~~~~~~
P(l\to \bar{a}, \bar{b})=\frac{1}{4},~~~~~~~~~~P(\bar{l})=\frac{1}{3}.
$$
Together with the axioms, this information is sufficient to answer any question.
The corresponding joint probabilities are shown in the table to the right.
For example, in binary logic, from $L,\bar{A}$ neither $B$, nor its negation $\bar{B}$ can be deduced. Indeed, if someone is in the living room ($L$) and Alice is not in her bedroom, then Bob may either be with her in the living room or in his own bedroom (trust this, the truth set of $L\,\bar{A}$ is not a subset of either $B$, or $\bar{B}$). In probability theory, a definitive conclusion cannot be made either, but probabilistic reasoning is possible: $$ P(l,\bar{a}\to b) = \frac{P(\bar{a}, b, l)}{P(\bar{a},l)} = \frac{1/3}{1/2} = \frac{2}{3}. $$ In interval logic even stronger results can be obtained under conditions of uncertainty.
Predicate probabilities
In conclusion, let’s briefly consider a formal theory constructed using predicates. As before, we will assume that the probability of an axiom like $\forall_x \,A(x)$ is equal to one. If the probability of a conjunction is equal to one, then the probabilities of each argument in the conjunction are also equal to one: $$ P(A(x_1)\,\&\,A(x_2)\,\&\,...) = 1~~~~~~~~~~\Rightarrow~~~~~~~~~~~~\forall_x \,[\,P\bigr(A(x)\bigr)= 1\,]. $$ Thus, the theorems $\forall_x\, A(x)$ of binary predicate logic have unit probabilities $P\bigr(A(x)\bigr)=1$ for any object in the theory.
◊ As an example, consider the relation $(x\,\text{in}\,y)$ from common knowledge: object $x$ is inside object $y$. It satisfies the following axioms of strict tree order (universal quantifiers omitted): $$ \begin{array}{lll} \neg(x~\text{in}~x) & ~~~~~~ & (1) & \text{anti-reflexivity}\\ (x~\text{in}~z)\,\&\,(z~\text{in}~y)~\to~(x~\text{in}~y) & & (2) & \text{transitivity}\\ (z~\text{in}~x)\,\&\,(z~\text{in}~y)~\to~(x~\text{in}~y)\vee(y~\text{in}~x)\vee(x=y) & & (3) & \text{tree structure} \end{array} $$
From anti-reflexivity and transitivity, asymmetry of the relation follows: $$ \begin{array}{lll} (y~\text{in}~x)~\to~\neg (x~\text{in}~y) &~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ & (4) & \text{asymmetry}\\ \end{array} $$ Let’s prove this using probabilistic methods. For any objects, from the first two axioms, we have the following relations between probabilities: $$ P(x~\text{in}~x) = 0,~~~~~~~~~~~~~~~P(x~\text{in}~z,~z~\text{in}~y) = P(x~\text{in}~y). $$ Setting $y=x$, we get: $$ P(x~\text{in}~z,~z~\text{in}~x)=0~~~~~~\Rightarrow~~~~~ P\bigr(\,\neg(x~\text{in}~z~\,\&\,~z~\text{in}~x)\,\bigr)=P\bigr(\,\neg(x~\text{in}~z)\vee\neg(z~\text{in}~x)\,\bigr)=1. $$ From this, using the implication unit rule, we obtain asymmetry: $P\bigr(\,(x~\text{in}~z)~\to~ \neg(z~\text{in}~x)\,\bigr)=1$.
