ML: Fuzzy Logic
Introduction
The uncertainty of a certain statement may arise due to a lack of information or uncertainty about the outcomes of future events. In such cases, probabilistic logic is usually applied. However, sometimes everything about the statement is known, yet it cannot be considered either true or false. Usually these are evaluative, comparative judgments: "Masha is beautiful" (but still not a dream); "The coffee is hot" (but already drinkable). Evaluative in nature are also oppositional fuzzy quantifiers:
A relation can be fuzzy: $\text{in}(x,y)$ – "object $x$ is inside object $y$". For example, "a pencil in a case" may stick out a little, yet still be inside it.
Finally, rules can also be fuzzy:
Logical connectives
Let's assume that an evaluative statement $A$ is characterized by a degree of truth $T_A$, which is a real number in the range $[0...1]$. The value $T_A=0$ corresponds to a false statement, and $T_A =1$ to a true one. Intermediate values represent "intermediate truth". For example, $T_A=0.7$ for $A:$ "Masha is beautiful" means that the statement is more true than false.
The degree of truth of the logical negation "NOT $A$" is naturally defined as follows:$$ \neg A:~~1-T_A. $$
For logical AND, OR, the minimum and maximum of the truth degrees of the statements are most often used: $$ A\,\&\,B:~~~\min(T_A,T_B),~~~~~~~~~~~~~A\vee B:~~~\max(T_A,T_B). $$ Recall that in probability theory the inequalities $P(A\,\&\,B)\le \min(P_A,\,P_B)$ and $ \max(P_A,\,P_B)\le P(A\vee B)$ hold for any two events. Fuzzy logic is not equivalent to probability theory or probabilistic logic and uses the upper bound for conjunction ($\,\&\,$) and the lower for disjunction ($\vee $).
Below, the figures show height maps for the truth degrees of logical operations:
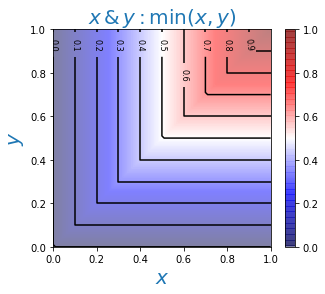
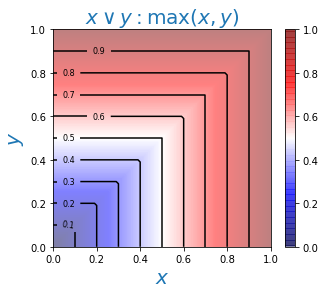
Thus, the logical connectives defined in this way satisfy all the axioms of Boolean algebra, except for the law of the excluded middle: $$ A\vee \neg A = 1,~~~~~~~~~~~~~~~A\,\&\,\neg A = 0. $$ It is worth checking this, for example, for $T_A=0.5$. Violation of this law is typical for multi-valued logics, in which the requirement that a statement must be either true or false, obviously, loses its meaning.
Note that in probabilistic logic the truth degree $P(A\,\&\,B)$ depends not only on $P(A)$ and $P(B)$, but also on the degree of correlation (dependence) of these statements (events). In fuzzy logic, such correlation is ignored.
Further, if this does not lead to ambiguity, instead of $T_A$ we will simply write $A$. Then for negation $\neg A=1-A$, disjunction $A\vee B =\max(A,B)$ and conjunction $A\,\&\, B =\min(A,B)$.
Fuzzy sets
It is convenient to describe the truth of evaluative judgments using set theory. When we say "Masha is beautiful," we imply the set of beautiful women, to which Masha belongs with some degree of accuracy.
Thus, in fuzzy set theory, a membership function $\mu_A(x)$ is introduced, which characterizes the degree of membership of an object $x$ to a set $A$: $x\in A$. The values of this function lie in the interval $[0...1]$, where $1$ means definitely belongs, and $0$ means definitely does not belong.
 The union $A\cup B$ of fuzzy sets $A$, $B$
corresponds to disjunction (OR), and the intersection $A\cap B$ to conjunction (AND).
Therefore, their membership functions are equal to:
$$
\begin{array}{lll}
\mu_{A\cap B}(x) = \min\{ \mu_A(x),~\mu_B(x)\},\\
\mu_{A\cup B}(x) = \max\{ \mu_A(x),~\mu_B(x)\}.
\end{array}
$$
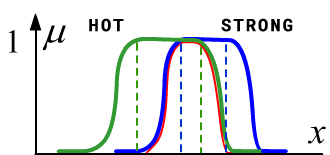
On the right, the set of various cups of coffee is shown as a line $x$
(these objects are not ordered and are usually drawn
as regions on a plane). Each cup corresponds to a certain value of its membership to
the sets "hot" and "strong".
The dashed lines are the boundaries of crisp sets. The red line is the membership function
of the intersection of sets ($\min$).
The union $A\cup B$ of fuzzy sets $A$, $B$
corresponds to disjunction (OR), and the intersection $A\cap B$ to conjunction (AND).
Therefore, their membership functions are equal to:
$$
\begin{array}{lll}
\mu_{A\cap B}(x) = \min\{ \mu_A(x),~\mu_B(x)\},\\
\mu_{A\cup B}(x) = \max\{ \mu_A(x),~\mu_B(x)\}.
\end{array}
$$
On the right, the set of various cups of coffee is shown as a line $x$
(these objects are not ordered and are usually drawn
as regions on a plane). Each cup corresponds to a certain value of its membership to
the sets "hot" and "strong".
The dashed lines are the boundaries of crisp sets. The red line is the membership function
of the intersection of sets ($\min$).
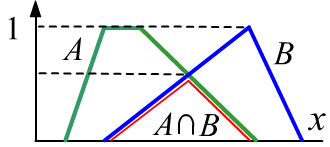 In this example, the fuzzy intersection includes the crisp intersection,
since its height (the maximum value) is equal to 1.
But in general, this may not be the case (if the height is less than 1).
A set is called normal if its height equals 1.
On the right is an example where the intersection is not normal.
In this example, the fuzzy intersection includes the crisp intersection,
since its height (the maximum value) is equal to 1.
But in general, this may not be the case (if the height is less than 1).
A set is called normal if its height equals 1.
On the right is an example where the intersection is not normal.
Inclusion or strict subset $A\subset B$ is by definition true, if $\mu_A(x) \lt \mu_B(x)$. Otherwise, it is false. This is a crisp logical concept. In various ways, one can also define fuzzy inclusion (for example, as the normalized sum $|\mu_A(x)-\mu_B(x)|$ over all elements $x$ of the set).
A cut of a fuzzy set $A$ at level $\alpha$ is defined as the set of elements for which the membership function is greater than the level: $\{x|~ \mu_A(x) \ge \alpha\}$. These elements belong to $A$ with accuracy not less than $\alpha$.
The logical statement "the coffee is hot and strong" means that there exists a set of various cups of coffee. Some of them belong to the set "hot", and some to the set "strong". The given cup (the one referred to in the statement) belongs to both sets (in the fuzzy sense).
Fuzzy predicates
In binary logic, statements are a special case of predicates. A predicate is a logical function (values $0,1$) of subject variables: $A(x),~ B(x,y)$. Subject variables are elements of certain sets (the domain of definition of the predicate). Examples of predicates: $P(x)$ – the number $x$ is positive, $M(x,y)$ – some $x$ is the mother of $y$, $A \in \alpha$ – the point $A$ lies on the line $\alpha$.
In fuzzy logic, the values of predicates naturally lie in the range $[0...1]$. Unary predicates $A(x)$ are fuzzy membership functions of element $x$ to the set $A$. Above, for $x\in A$ we used $\mu_A(x)$, now for brevity we will simply write $A(x)$.
Special cases of fuzzy predicates are fuzzy variables and relations.
Fuzzy variables
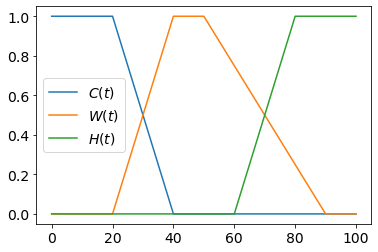 A fuzzy variable is a predicate depending on one or several real numbers.
For example, when talking about coffee, we can define the following
fuzzy variables depending on its temperature $t$:
A fuzzy variable is a predicate depending on one or several real numbers.
For example, when talking about coffee, we can define the following
fuzzy variables depending on its temperature $t$:
Other examples: slow, fast (functions of speed); light, heavy (functions of mass); young, old (functions of age), etc.
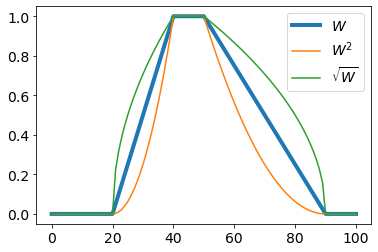 Various modifiers can be applied to fuzzy variables:
$$
\text{very}:~~~~A^2(x),~~~~~~\text{not very}:~~~~\sqrt{A(x)}.
$$
Thus "very warm"
$W^2(t)$ strengthens the function $W(t)$, while "not very warm" $\sqrt{W(t)}$ weakens it.
The first modifier is also called concentration,
and the second – dilution.
Various modifiers can be applied to fuzzy variables:
$$
\text{very}:~~~~A^2(x),~~~~~~\text{not very}:~~~~\sqrt{A(x)}.
$$
Thus "very warm"
$W^2(t)$ strengthens the function $W(t)$, while "not very warm" $\sqrt{W(t)}$ weakens it.
The first modifier is also called concentration,
and the second – dilution.
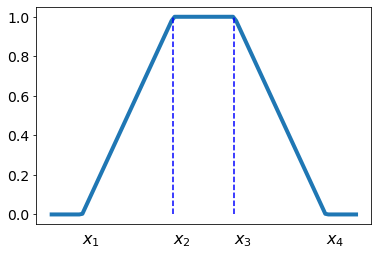
Here is an example of constructing a trapezoidal membership function depending on one real variable, in Python using the NumPy library:
def tra(min_X, x1,x2,x3,x4, max_X, num=100):
X = np.linspace(min_X, max_X, num, dtype = 'float32')
Y = np.zeros_like(X)
idx = (X >= x1) & (X <= x2); Y[idx] = (X[idx]-x1)/(x2-x1)
idx = (X > x2) & (X <= x3); Y[idx] = 1
idx = (X > x3) & (X <= x4); Y[idx] = (x4-X[idx])/(x4-x3)
return X,Y
Fuzzy relations
A fuzzy relation is a predicate depending on two subject variables. The function $R(x,y)$ assigns to a given pair of entities $x,y$ (subject constants) a real number from the range $[0...1]$ (the degree of truth of the relation). For example, for the relation "two numbers are almost equal" $x\approx y$ one can set $R(x,y)=e^{-(x-y)^2}.$ Then $R(x,x)=1$; if $x$ and $y$ are close, then $R(x,y)\approx 1$; otherwise, $R(x,y)\to 0$.
In binary logic, the relation $R(x,y)$ is a subset of the set of pairs (Cartesian product) $\mathbb{X}\times \mathbb{Y}$. Therefore, a fuzzy relation is a fuzzy set. All definitions (union, intersection, complement of relations, etc.) carry over without change.
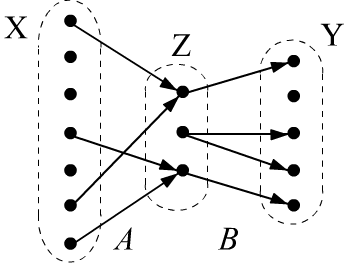 Let's consider in more detail the composition $(A \circ B)(x,y)$ of two relations $A(x,z)$ and $B(z,y)$.
Assume there are three sets $\mathbb{X},\mathbb{Z},\mathbb{Y}$ (generally different).
The relation $A(x,z)$ is defined on the set $\mathbb{X}\times \mathbb{Z}$,
and the relation $B(z,y)$ on the set $\mathbb{Z}\times \mathbb{Y}$.
In binary logic, if $A(x_i,z_k)$ is true, then the elements $x_i$ and $z_k$ are linked by relation $A$.
This can be represented as an arrow from $x_i$ to $z_k$ (see the figure on the right).
The composition of relations $(A \circ B)(x_i,y_j)$ is true,
if from $x_i$ one can "reach" $y_j$ through some $z_k$. Formally this is expressed
using the existential quantifier (there exists $z$ such that ...):
$$
(A \circ B)(x,y) : ~~~~~~\exists_z\, A(x,z)\,\&\,B(z,y) = \bigr[A(x,z_1)\,\&\,B(z_1,y)\bigr]\vee \bigr[A(x,z_2)\,\&\,B(z_2,y)\bigr]\vee ...,
$$
where the existential quantifier is expressed as a "sum" of logical OR across all elements of a finite set $\mathbb{Z}$.
For fuzzy relations this definition generalizes naturally:
$$
(A \circ B)(x,y) = \max_z \bigr[\min\{A(x,z),~B(z,y)\}\bigr],
$$
where the $\max$ is taken over all elements $z\in \mathbb{Z}$.
Let's consider in more detail the composition $(A \circ B)(x,y)$ of two relations $A(x,z)$ and $B(z,y)$.
Assume there are three sets $\mathbb{X},\mathbb{Z},\mathbb{Y}$ (generally different).
The relation $A(x,z)$ is defined on the set $\mathbb{X}\times \mathbb{Z}$,
and the relation $B(z,y)$ on the set $\mathbb{Z}\times \mathbb{Y}$.
In binary logic, if $A(x_i,z_k)$ is true, then the elements $x_i$ and $z_k$ are linked by relation $A$.
This can be represented as an arrow from $x_i$ to $z_k$ (see the figure on the right).
The composition of relations $(A \circ B)(x_i,y_j)$ is true,
if from $x_i$ one can "reach" $y_j$ through some $z_k$. Formally this is expressed
using the existential quantifier (there exists $z$ such that ...):
$$
(A \circ B)(x,y) : ~~~~~~\exists_z\, A(x,z)\,\&\,B(z,y) = \bigr[A(x,z_1)\,\&\,B(z_1,y)\bigr]\vee \bigr[A(x,z_2)\,\&\,B(z_2,y)\bigr]\vee ...,
$$
where the existential quantifier is expressed as a "sum" of logical OR across all elements of a finite set $\mathbb{Z}$.
For fuzzy relations this definition generalizes naturally:
$$
(A \circ B)(x,y) = \max_z \bigr[\min\{A(x,z),~B(z,y)\}\bigr],
$$
where the $\max$ is taken over all elements $z\in \mathbb{Z}$.
The following axioms often occur to fix the properties of relations: $$ \begin{array}{lllll} \text{reflexive} & R(x,x) = 1 \\ \text{antireflexive} & R(x,x) = 0 \\ \text{symmetric} & R(x,y) = R(y,x) \\ \text{asymmetric} & \min\bigr\{R(x,y),\,R(y,x)\bigr\} = 0 \\ \text{antisymmetric} & x\neq y ~\Rightarrow~ \min\bigr\{R(x,y),\,R(y,x)\bigr\} = 0 \\ \text{transitive} & \min\bigr\{R(x,y),\,R(y,z)\bigr\} \le R(x,z) \\ \end{array} $$ For example, the proximity relation $x\approx y$ is reflexive and symmetric.
T-norm and T-conorm *
The choice of the functions $\min$ for conjunction (intersection) and $\max$ for disjunction (union) is not the only possible one (although often it is more preferable). Let's denote logical AND as the function $T(x,y)$ (norm), and logical $OR$ as $S(x,y)$ (conorm). We require that they be symmetric and associative: $$ \begin{array}{llll} \&:~ \\ \vee\,:\\ \end{array}~~~~~~~~~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} T(x,y) &=& T(y,x) \\ S(x,y) &=& S(y,x) \end{array}\right.,~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} T(x, T(y,z)) &=& T(T(x, y),z)\\ S(x, S(y,z)) &=& S(S(x, y),z)\\ \end{array}\right.. $$ In addition, let us impose the properties of boundedness and monotonicity (holding for $\&, \vee$ also in binary logic): $$ \begin{array}{llll} \&:~ \\ \vee\,:\\ \end{array}~~~~~ \left\{ \begin{array}{llll} T(0,0) = 0, & T(1,x) = x\\ S(1,1) = 1, & S(0,x) = x\\ \end{array} \right.,~~~~~~~ \left\{ \begin{array}{llll} x_1 \le x_2,~~~ y_1 \le y_2~~~\Rightarrow~~~~~T(x_1, y_1) \le T(x_2, y_2)\\ x_1 \ge x_2,~~~ y_1 \ge y_2~~~\Rightarrow~~~~~S(x_1, y_1) \ge S(x_2, y_2)\\ \end{array} \right.. $$Note that the monotonicity condition holds not only in Boolean logic, but is also quite natural for fuzzy logic. For example: $0.5 \,\&\, 0.8 ~\lt~ 0.7 \,\&\, 0.9$ means that $0.5$ is less true than $0.7~~~$ AND $~~~0.8$ is less true than $0.9$.
We will also assume that De Morgan's laws hold $\neg(X\,\&\,Y) = \neg X\vee \neg Y$ and $\neg(X\vee Y) = \neg X\,\&\, \neg Y$, which connect these two operations: $$ \begin{array}{llll} 1-T(x,y) = S(1-x,1-y), & ~~~~~ & 1-S(x,y) = T(1-x,1-y). \\ \end{array} $$ There are various functions that satisfy these axioms (typically, for example, $T(x,y)$ is defined,, and $S(x,y)$ s derived from De Morgan’s law). For example, consider the following three variants: $$ \begin{array}{l|c|c|l|l|} & \text{1. logical} & \text{2. algebraic} & \text{3.} \\ \hline A\,\&\,B & \min(A,B) & A\,B & \max(A+B-1,~ 0) \\ A\vee B & \max(A,B) & A+B - A\,B & \min(A+B,~ 1) \\ \hline A \,\&\, A \equiv A & \mathbb{T} & (0,1) & (0, 1) \\ A \vee A \equiv A & \mathbb{T} & (0,1) & (0, 1) \\ A \,\&\, \neg A & (0.0,0.5) & (0,0.25) & \mathbb{F} \\ A \vee \neg A & (0.5,1.0) & (0.75,1) & \mathbb{T} \\ A\,\&\,(B\vee C) \equiv~... & \mathbb{T} & (0,1) & (0, 1) \\ A\vee (B\,\&\,C)\equiv~... & \mathbb{T} & (0,1) & (0, 1) \\ \end{array} $$ Under the definition of connectives, the truth values of some identities of Boolean algebra are indicated when using these connectives. If $\mathbb{T}$ is indicated, the identity always holds; if $\mathbb{F}$, it is always false; otherwise, the ranges of possible truth values are given for all argument assignments.
Note that the law of the excluded middle is valid for variant (3.), whereas in the other cases $A \,\&\, \neg A$ tends to be mostly false, and $A \vee \neg A$ tends to be mostly true. The properties of idempotence: $$ A\,\&\,A \equiv A,~~~~~~~~~~~~A\vee A \equiv A. $$ are satisfied only for the "logical" variant ($\min,\max$). In fact, these are very natural properties both for logical values and for sets ($A\cap A=A$ and $A\cup A=A$). Therefore, usually, their fulfillment is desirable.
Let's also note that for definitions 2,3 the laws of distributivity are violated: $$ \begin{array}{lcl} A\,\&\,(B\vee C) &\equiv& (A\,\&\,B)\vee (A\,\&\,B)\\ A\vee(B\,\&\,C) &\equiv& (A\vee B)\,\&\, (A\vee B). \end{array} $$ While this is not particularly critical, it does not fully align with the standard intuitive interpretation of logical operations.
Implication
In Boolean logic, implication plays an important role: $A\to B$. This logical connective in language corresponds to the phrases: "from $A$ follows $B$", "if $A$, then $B$". It is accepted that it is false only for $1\to 0$ ("from truth one cannot obtain falsehood"). In all other cases: $0\to 0$, $0\to 1$, $1\to 1$ it is true.
It is usually assumed that there is some connection between the premise $A$ and the consequence $B$ of the implication $A\to B$.
Thus, in arithmetic, for any $x$ the formula $(x<2) \to (x<4)$ is true.
When the premise is true ($x=1$), the consequence is also true.
If the premise is false, then the consequence may be either true (for $x=3$),
or false ($x=5$).
The "less correct" statement $(x > 2) \to (x < 4)$ is false for $x=5$.
In fuzzy logic, there is no single consensus on which expression should be used for implication. Below are some variants proposed by different authors:
$$ A\to B:~~~~~~~~~~~~~~~~~~~ \begin{array}{lll} \text{Kleene} & \neg A \vee B & ~~~~~ & \max(1-A,~B) \\ \text{Zadeh} & \neg A \vee (A\,\&\,B)& & \max(1-A,~\min(A,B)) \\ \text{Wadie} & & & \max(1-A, ~A\,B)\\ \\ \text{Sharp} & & & \text{if}(A \le B)~ \{1,~0\} \\ \text{Brouwer} & & & \text{if}(A \le B)~ \{1,~B\} \\ \text{Łukasiewicz} & & & \text{if}(A \le B)~ \{1,~B+1-A\} \\ \text{Goguen} & & & \text{if}(A \le B)~ \{1,~B/A\}, \\ \end{array} $$where the construction $\text{if}(C)\{A, B\}$ equals $A$, if $C$ is true, and $B$ otherwise. All these definitions reproduce Boolean implication for the values $0,1$.

The first three definitions are based on expressing implication through disjunction in binary logic. In Kleene’s definition, this is written explicitly. In Zadeh’s case, under distributivity (for $\&=\min,$ $\vee=\max$), one can write $(\neg A \vee A)\,\&\,(\neg A \vee B)$. The first bracket in binary logic equals $1$. In fuzzy logic (with $\min$, $\max$) it is greater than $0.5$ and the closer to $1$, the truer $A$ is. The numerical values of these implications differ if one of the arguments is near the indeterminate value $0.5$.
The last four definitions proceed from the fact that implication must be strictly true, if from a less true statement it "follows" a not less true one ($A \le B$). Differences arise when $A$ is truer than $B$.
Logical inference
 In binary logic, $P$ logically implies $Q$
if whenever the formula $P$ is true, the formula $Q$ is also true.
This is denoted as $P\Rightarrow Q$.
Logical inference is a way of obtaining some true formulas from others that are also true.
It should not be confused with implication $P\to Q$, which is a logical connective
taking the values $0$ or $1$.
In binary logic, $P$ logically implies $Q$
if whenever the formula $P$ is true, the formula $Q$ is also true.
This is denoted as $P\Rightarrow Q$.
Logical inference is a way of obtaining some true formulas from others that are also true.
It should not be confused with implication $P\to Q$, which is a logical connective
taking the values $0$ or $1$.
Let us consider the simplest example of logical inference: if the conjunction of statements is true, then each of the statements is also true (derivable). In fuzzy logic, this rule is generalized in an obvious way, leading to interval estimates for the derived formula: $$ A\,\&\,B~~~~~ \Rightarrow~~~~~~ A,~~~~~~~~~~~~~~~~~~~~~~\min(A,~B) ~~~\le~~~ A ~~~\le~~~ 1, $$ where $\min(A,~B)$ on the one hand is the value of the conjunction $A\,\&\,B$, and on the other hand, the lower bound for $A$. Naturally, in this inference it is assumed that the truth value of $A\,\&\,B$ is given, and as a result of logical inference, it serves as the lower bound for the truth value of $A$. The inequalities for the following inference are interpreted similarly: $$ A~~~~~ \Rightarrow~~~~~~ A\vee B,~~~~~~~~~~~~~~~~~~~~~~0 ~~~\le~~~ A ~~~\le~~~ \max(A,~B). $$
Thus, in fuzzy logic, besides indicating the derived formula, it is necessary to be able to compute its truth value. The definition of such logical inference is not entirely unambiguous, which is reflected in the variety of proposed variants of implication between two statements.
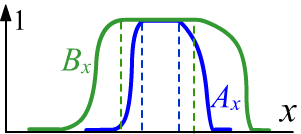 One of the possibilities, as in probabilistic logic,
is to assume that $A~\Rightarrow~B$ if $A \le B$.
The inference examples given above satisfy this condition.
In the case of predicates defined on the same set
$\mathbb{X}$, such inference $A(x)~\Rightarrow~B(x)$ means that $A\subset B$ and the sets $A,B$
are normal, i.e., they have unit height (see the figure on the right).
Then, on the cut $\alpha=1$, $A$ will be an ordinary subset of $B$.
One of the possibilities, as in probabilistic logic,
is to assume that $A~\Rightarrow~B$ if $A \le B$.
The inference examples given above satisfy this condition.
In the case of predicates defined on the same set
$\mathbb{X}$, such inference $A(x)~\Rightarrow~B(x)$ means that $A\subset B$ and the sets $A,B$
are normal, i.e., they have unit height (see the figure on the right).
Then, on the cut $\alpha=1$, $A$ will be an ordinary subset of $B$.
Knowledge (common or mathematical) is often formulated as "IF ... THEN ..." rules
(implication).
Then in binary logic
the important methods of inference are modus ponens and modus tollens
(writing the premises of the inference separated by commas implies
they are connected by logical AND):
$$
\begin{array}{cccccc}
A, & A\to B&~~~~~~~~&\Rightarrow&~~~~~~~~&B\\
\neg B,& A\to B&~~~~~~~~&\Rightarrow&~~~~~~~~&\neg A\\
\end{array}
$$
Assuming these inferences hold in fuzzy logic,
let's find the truth values of the resulting formulas.
For modus ponens we have $\min(A,~A\to B) ~\le~ B~\le~ 1$. In the case when the "axiom" $A \to B$ is always true, then $A \le B$. If $A=1$, then $B=1$ (the binary case), and if $A=0$, we have $0 \le B\le 1$, i.e. the value of $B$ is completely undefined (which is also consistent with binary logic). For modus tollens for a true rule $A \to B$ we also obtain $$ A ~\le~ B ~\le~ 1. $$ Recall that obtaining the truth value of the derived formulas in the form of an inequality is also typical for probabilistic logic.
When the truth value of the rule $A\to B$ differs from $1$, it is necessary to choose a particular formula for implication. It should also be noted that among all definitions of implication, with the inequality $\min(A,~A\to B) \le B$, only Sharp and Brouwer implications are consistent in the general case.
Let's consider a simple example with two rules: $$ A\to B,~~~~~~~\neg A\to \neg B. $$ For instance, they are valid for $A$: "hit the glass hard", $B$: "the glass will break". From the first rule it follows that $A \le B$, and from the second $1-A \le 1-B$ or $B\le A$. Therefore $B = A$ (the exact value given $A$). This is a natural result: if the glass is hit lightly ($A = 0.2$), then apparently it will not break ($B = 0.2$).
✒ In binary logic there exists a very powerful method of resolution inference, applied in automated reasoning: $$ A\vee C,~\neg A\vee B~~~~~~~~~~\Rightarrow~~~~~~~~~~C\vee B. $$ In fuzzy logic it does not work, since the inequality $\min\bigr(\max(A,C),~\max(1-A, B)\,\bigr)~\le \max(C,B)$ is not valid (for example, for $A=1/2,~B=C=0$). This is due to the violation of the law of the excluded middle. In binary logic, resolution means that if the premises are true, then either $A=0$ and then $C=1$, $B$ is arbitrary, or $A=1$ and then $B=1$, $C$ is arbitrary. Therefore, in any case $B \vee C$ is true.
Zadeh’s inference for predicates
Zadeh’s inference generalizes the rule of modus ponens to the case of fuzzy predicates. Suppose there is a rule $A(x)\to B(y)$ and a predicate $A'(x)$ “similar” to $A(x)$. Then: $$ A'(x),~~A(x)\to B(y)~~~~~~~~~\Rightarrow~~~~~~~B'(x) = A'\circ (A\to B) = \max_x\bigr[ \min\bigr[ A'(x),~ A(x)\to B(y)\bigr]\bigr]. $$ A fuzzy rule $A(x)\to B(y)$ can be given in the form of a relation (a matrix $\mathbb{X}\times\mathbb{Y}$) or computed using the given predicates $A(x), B(y)$ and one of the definitions of implication (which is simpler).
In the special case of statements $A'=A$ and Brouwer’s implication $A\to B:~R=\text{ if }(A \le B): \{~1;~ B\}$, we obtain: $$ B' = \left\{ \begin{array}{llll} \min(A,~1)=A, & ~~~& A \le B \\ \min(A,~B)=B, & ~~~& A \gt B \end{array} \right. ~~~~~=~~~~ \min(A,B) $$ If $A=1$, then $B'= B = R$ (the truth degree of the rule); if $A=0$, then $B'=0$ (?), although in binary logic the truth of $B$ is undefined. For $A=0.5$ we have $B'=0.5$.
Mamdani inference
Mamdani’s logical inference is a heuristic method for fuzzy reasoning, used when there is a set of rules containing fuzzy variables. Suppose, for example, there are two rules depending on six fuzzy variables $A_i,B_i,C_i$, defined by three parameters $x,y,z$: $$ \begin{array}{llll} A_1(x) \,\&\,B_1(y) \to C_1(z),\\ A_2(x) \,\&\,B_2(y) \to C_2(z).\\ \end{array} $$ Assume the real parameter values $x,y$ are known and equal to $x_0,y_0$.The task is to determine the most appropriate value of parameter $z$ that satisfies these rules.
At the first stage of finding $z$, fuzzification is performed (obtaining the values
of fuzzy variables $A_1(x_0)$, etc.)
and the premises are evaluated based on fuzzy logic formulas ($\min$ for $\&$ and $\max$ for $\vee$):
$$
\left\{
\begin{array}{llll}
\alpha_1 = \min\bigr(A_1(x_0),~B_1(y_0)\bigr) \\
\alpha_2 = \min\bigr(A_2(x_0),~B_2(y_0)\bigr)
\end{array}\right.,
~~~~~~~~~~~~~~
\left\{
\begin{array}{llll}
\alpha_1 \to C_1(z)\\
\alpha_2 \to C_2(z)\\
\end{array}\right..
$$
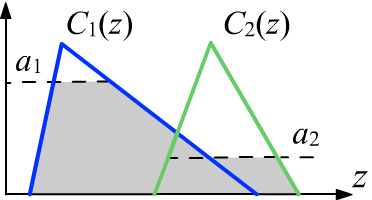 Then the rule consequents are "activated", assuming
that their truth value should not exceed the truth of the premises (on the right in the figure, the levels $\alpha_i$
cut off the higher truth values of the consequents):
$$
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~C'_i(z) = \min (\alpha_i, C(z)).
$$
These modified consequents are combined
across all rules (logical OR), resulting in
a distribution function $\mu(z)\in[0...1]$ for the variable $z$:
$$
\mu(z) = \max_i C'_i(z).~~~~~~
$$
At the final stage, defuzzification is performed, resulting in
a specific value for $z$.
For example, one can take
the centroid of the function $\mu(z)$:
$$
z_0 =\int z\,\mu(z)\,dz ~\Bigr/~ \int \mu(z)\,dz.
$$
Note that, both at the activation stage and during defuzzification,
premises with low truth values give little contribution to the result
(completely false premises do not affect it at all).
Therefore, instead of the $\min$ function, one can also
use multiplication: $C'_i(z)=\alpha_i\,C_i(z)$ (Larsen’s algorithm).
Then the rule consequents are "activated", assuming
that their truth value should not exceed the truth of the premises (on the right in the figure, the levels $\alpha_i$
cut off the higher truth values of the consequents):
$$
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~C'_i(z) = \min (\alpha_i, C(z)).
$$
These modified consequents are combined
across all rules (logical OR), resulting in
a distribution function $\mu(z)\in[0...1]$ for the variable $z$:
$$
\mu(z) = \max_i C'_i(z).~~~~~~
$$
At the final stage, defuzzification is performed, resulting in
a specific value for $z$.
For example, one can take
the centroid of the function $\mu(z)$:
$$
z_0 =\int z\,\mu(z)\,dz ~\Bigr/~ \int \mu(z)\,dz.
$$
Note that, both at the activation stage and during defuzzification,
premises with low truth values give little contribution to the result
(completely false premises do not affect it at all).
Therefore, instead of the $\min$ function, one can also
use multiplication: $C'_i(z)=\alpha_i\,C_i(z)$ (Larsen’s algorithm).
There is a modification of this method — Tsukamoto inference. At the activation stage, the equations $C_i(z) = \alpha_i$ are solved, giving unique solutions $z_i$. This approach is possible only when the fuzzy variables $C_i(z)$ in the rules are monotonic functions of $z$ (increasing or decreasing), otherwise there would be multiple solutions. At the defuzzification stage, the centroid is also computed based on the obtained solutions $z_1,z_2,...$: $$ z= \sum_i \alpha_i z_i~\Bigr/~\sum_i\alpha_i. $$
There is also the Sugeno approach, in which the consequents in the rules are written in the form of instructions for the values $z=F(x,y)$, where $F$ are some functions (usually linear). After fuzzification, we immediately obtain the values $z_i$, and as above, using the premise truth values $\alpha_i$, the centroid is computed.
Fuzzy numbers
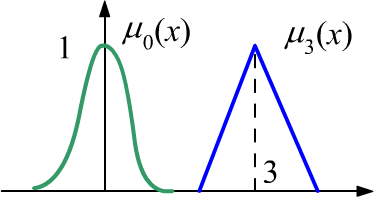 A fuzzy number $X$ is a membership function $\mu_X(x)$ of a real number $x$,
which has a single unit maximum at $x=X$. In the figure on the right, $\mu_0(x)$ is
"approximately zero," and $\mu_3(x)$ is "approximately three."
A fuzzy number $X$ is a membership function $\mu_X(x)$ of a real number $x$,
which has a single unit maximum at $x=X$. In the figure on the right, $\mu_0(x)$ is
"approximately zero," and $\mu_3(x)$ is "approximately three."
Let there be a real function of two (ordinary) numbers $z=f(x,y)$ and two fuzzy numbers $A(x), B(y)$. We are interested in the membership function $\mu_{f(A,B)}(z)$, which equals the degree of confidence that a particular number $z$ is the result of applying the operation (function) $f$.
We iterate through all possible values $x,y$ such that $z=f(x,y)$ and determine the degrees of confidence that these are fuzzy numbers $A(x), B(y)$. Then, according to Zadeh’s extension principle, the membership function of the operation, by definition, will be equal to: $$ \mu_{f(A,B)}(z) = \sup_{x,y: f(x,y)=z}\min\bigr\{\mu_A(x),\,\mu_B(y)\bigr\}. $$ Thus, from all possible "crisp" ways to obtain $z$ we choose the one that gives the greatest ($\sup$) value of the minimum of the membership functions of the fuzzy number arguments of the function.
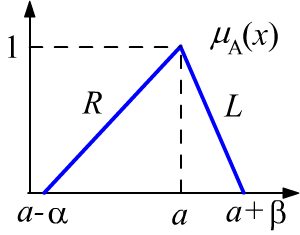 Often, $L-R$ type membership functions are used for fuzzy numbers:
$$
\mu_A(x) =
\left\{
\begin{array}{lll}
L(a-x) & x \ge a \\
R(x-a) & x \ge a \\
\end{array}
\right.
~~~~~~~
\begin{array}{lll}
L(0)=R(0) = 1 \\
L,R \text{ - non-increasing} \\
\end{array}
$$
The simplest example is the triangular membership function $\langle a;\, \alpha, \beta \rangle$, shown in the figure.
Using the extension principle for triangular numbers,
one can obtain the following results for standard arithmetic operations:
$$
\begin{array}{lll}
\langle a_1;\, \alpha_1,\beta_1 \rangle \pm \langle a_2;\, \alpha_2,\beta_2 \rangle
= \langle a_1\pm a_2;\, \alpha_1+\alpha_2,\beta_1+\beta_2 \rangle\\
\langle a_1;\, \alpha_1,\beta_1 \rangle \cdot \langle a_2;\, \alpha_2,\beta_2 \rangle
= \langle a_1\cdot a_2;\, \alpha_1 a_2+\alpha_2 a_1,\beta_1 b_2+\beta_2 b_1\rangle\\
\langle a;\, \alpha,\beta \rangle^{-1} = \langle 1/a;\, \beta/a^2,\alpha/a^2 \rangle \\
\end{array}
$$
Note that for the position of the maximum, ordinary arithmetic operations are applied,
while the fuzziness (the width of the triangle) increases.
Often, $L-R$ type membership functions are used for fuzzy numbers:
$$
\mu_A(x) =
\left\{
\begin{array}{lll}
L(a-x) & x \ge a \\
R(x-a) & x \ge a \\
\end{array}
\right.
~~~~~~~
\begin{array}{lll}
L(0)=R(0) = 1 \\
L,R \text{ - non-increasing} \\
\end{array}
$$
The simplest example is the triangular membership function $\langle a;\, \alpha, \beta \rangle$, shown in the figure.
Using the extension principle for triangular numbers,
one can obtain the following results for standard arithmetic operations:
$$
\begin{array}{lll}
\langle a_1;\, \alpha_1,\beta_1 \rangle \pm \langle a_2;\, \alpha_2,\beta_2 \rangle
= \langle a_1\pm a_2;\, \alpha_1+\alpha_2,\beta_1+\beta_2 \rangle\\
\langle a_1;\, \alpha_1,\beta_1 \rangle \cdot \langle a_2;\, \alpha_2,\beta_2 \rangle
= \langle a_1\cdot a_2;\, \alpha_1 a_2+\alpha_2 a_1,\beta_1 b_2+\beta_2 b_1\rangle\\
\langle a;\, \alpha,\beta \rangle^{-1} = \langle 1/a;\, \beta/a^2,\alpha/a^2 \rangle \\
\end{array}
$$
Note that for the position of the maximum, ordinary arithmetic operations are applied,
while the fuzziness (the width of the triangle) increases.
Another way of defining membership functions $\langle a,b; \alpha, \beta \rangle$ is a trapezoid with a maximum over the interval $[a,b]$ and boundary points $\alpha,\beta$.
Fuzzy logic in Python
Let's define a class with overloaded logical operators for fuzzy logic:
class Fuzzy:
def __init__(self, val=0):
val = np.array(val) if isinstance(val,(list, np.ndarray)) else np.array([val])
self.val = val.astype('float32')
def __invert__(self): # ~x NOT
return Fuzzy(1-self.val)
def __and__(self, other): # x & y AND
return Fuzzy( np.minimum(self.val, other.val) )
def __or__(self, other): # x | y OR
return Fuzzy( np.maximum(self.val, other.val) )
def __eq__(self, other):
return Fuzzy(self.val == other.val)
def __str__(self):
return f"{self.val[0]}" if len(self.val)==1 else f"{self.val}"
def minmax(self):
return (self.val.min(), self.val.max())
def __gt__(self, other):
return Fuzzy( np.minimum( np.ones_like(self.val), 1-self.val+other.val) )
Example of its usage:
x = Fuzzy( [0, 0, 0, 0.5,0.5,0.5,1, 1, 1] ) y = Fuzzy( [0, 0.5,1, 0, 0.5,1, 0, 0.5,1] ) print(x & y ) # [0. 0. 0. 0. 0.5 0.5 0. 0.5 1. ] print(x | y ) # [0. 0.5 1. 0.5 0.5 1. 1. 1. 1. ]Verification of Boolean algebra identities:
vals = np.linspace(0,1,101, dtype='float32') x = Fuzzy(vals) print ( (x & x).minmax() ) # (0.0, 1.0) print ( (x & ~x).minmax() ) # (0.0, 0.5) print ( (x | ~x).minmax() ) # (0.5, 1.0) x, y, z = np.meshgrid(vals, vals, vals) x, y, z = Fuzzy(x), Fuzzy(y), Fuzzy(z) print ( ((x & (y | z)) == ((x & y) | (x & z))).minmax() ) # (1.0, 1.0)