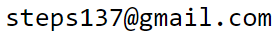ML: Interval Probabilistic Logic

---

Introduction

When accumulating everyday knowledge in the form of facts and rules, people rarely use binary logic.
Since knowledge is a generalization of experience, the degree of its truth has a probabilistic and fuzzy nature. Conclusions drawn from knowledge, using the available information, are also made under conditions of uncertainty. This document discusses an interval-probabilistic approach to logic. It is useful first to become familiar with the basics of probabilistic methods and the connection between logic and probability. Reading the informal introduction to logic may also be helpful. A direct continuation of this topic is the discussion of fuzzy logic.

---

Several examples

In the real world, there are no absolutely true or false statements. There are many reasons why one should move away from binary (yes–no) logic when evaluating the truth of statements:

• future events are always probabilistic in nature;
• there may be a lack of information about an event that has occurred;
• some events are unique and non-repeatable;
• attitudes toward an object or process are often evaluative or emotional.

Let's consider a few examples of statements about such events.

1. Probability. The statement "The coin that is about to be tossed will land heads up" is traditionally attributed to probability theory. If the coin is fair (symmetric) and tossed fairly ("randomly"), then statement $A$ is assigned a numerical characteristic $P(A)=1/2$, called the probability of event $A$. In practice, this number can be measured only after a large number of repetitions, and even then only under the assumption of a constant "true" probability. We move away from "pure" probability theory if we encounter this coin for the first time and it happens to be in the hands of a dubious individual.

2. Uncertainty. "There is a cat in the room". Although the cat is already either in the room (or not), this statement will only turn out to be true or false in the future (one must enter the room). If we are in this room for the first time, the truth of the statement is undefined (the cat may be there, or it may not).
It is important to distinguish this uncertainty from the probability $P(A)=1/2$ in the case of a coin, since we have no reason to assume that the cat’s presence in the room is an equally likely event. Naturally, if it is our own room and we don’t own a cat, the uncertainty decreases, though not completely (for example, if we forgot to close the window when leaving).

3. Conviction. "The count was most likely killed by the butler; he had a motive and no alibi". The murder has already occurred, and unlike the coin toss, it is fundamentally unrepeatable. Nevertheless, similar precedents in the past (with other crimes) allow us to make certain judgments.
At first, in the complete absence of information (no one saw the crime itself), it is impossible to give a definite evaluation of the statement’s truth. As evidence and motives accumulate, one can present arguments for and against the truth of the statement, gradually reducing its uncertainty.

4. Uniqueness. "This century, Earth will collide with the Moon" - this event, like all the previous ones, will either happen or not. However, it is unique, and purely probabilistic reasoning is not suitable. At the same time, it cannot be considered completely uncertain, since we have accumulated experience on the basis of which this event seems highly unlikely. Unlike the butler case, such experience can only refute the truth of the statement, but not confirm it (we have experience that collisions have not occurred, but no experience that they have).

5. Evaluation. "This coffee is strong and hot," "Masha is beautiful and strong," "The old car runs fast" - these are all evaluative judgments associated with fuzzy sets ("cups of coffee of different temperatures," "many beautiful women," etc.). Unlike the previous examples, where a statement is "actually" either true or false, here the law of the excluded middle $A\vee \neg A ~=~ \mathbb{T}$ (truth) does not apply. Such evaluative statements may be fully known, and yet they cannot be considered either true or false. Evaluative judgments can also be combined with probabilistic ones: "Tomorrow, it will most likely rain heavily".

In this document, we will rely on the relatively solid foundation of probability theory, assuming that a statement is "actually" either true or false, but we do not possess complete information. Generally speaking, measures of "confidence" in truth, or the degree of "evaluation" in an emotional judgment, may have a mathematical basis different from probability theory. Nevertheless, as far as possible, probabilistic logic will deal with tasks similar to the first four examples. The fifth example is addressed in the following document on fuzzy logic and set theory.

---

Probability of truth

From now on, when it does not lead to ambiguity, instead of writing the probability $P(A)$ of an event, we will simply write $A$, similarly $A\,\&\,B$ instead of $P(A\,\&\,B)$ and so on. In addition, two ways of describing the truth of a statement $A$ about some event or process will be used.

Point measure $A$, as usual, means the probability that the event will occur (or has already occurred).
The closer $A$ is to one, the "truer" the statement is. The negation $\neg A$ or $\bar{A}$ of a statement $A$ has probability: $$ \bar{A}=1-A. $$ At the same time, it is assumed that the identities of probability theory hold $A\vee B=A+B-(A\,\&\,B)$, as well as all identities of Boolean algebra: $\neg(A\,\&\,B) = \bar{A}\vee \bar{B}$, etc., including the law of the excluded middle $(A\,\&\,\bar{A})=0$.

Interval estimation is the second way of specifying the degree of truth of a statement $A$. We denote the lower bound of the interval by $a$, and the upper bound by $1-\bar{a}$: $$ A=[a,\,1-\bar{a}],~~~~~~~~~~a~\le~A ~\le~ 1-\bar{a},~~~~~~~~a+\bar{a}~\le~1, $$ where the last inequality means that the upper bound cannot be less than the lower one. When $a+\bar{a}=1$, the probability of the event is fully determined. Conversely, when $a=\bar{a}=0$, i.e. $A=[0,~1]$, the probability value is completely undefined. An interval estimate makes it possible to distinguish between a probabilistic but determined judgment $A=[0.5,\,0.5]$ (tossing a coin) and an indeterminate one $A=[0,\,1]$ (a cat in an unknown room).

Considering that always $\bar{A}=1-A$, for the probability interval of the negation we should write: $$ \bar{A}=[\bar{a},\,1-a]. $$ The intervals of a statement and its negation may either not overlap ($a+\bar{a} \gt 0.5$) - a more definite situation, or overlap (if $a+\bar{a} \le 0.5$) - a less definite one:

On the plane $(A,\bar{A})$ the possible values of the probabilities of a statement and its negation lie on the segment shown in bold in the figures.

A detective hypothesis "The butler killed the count" at the beginning of the investigation has indeterminate truth $[0,\,1]$. As the investigation progresses, it may be supported by facts in favor ($a$), or refuted by facts against($\bar{a}$). Naturally, even when the uncertainty is eliminated $(a+\bar{a}=1)$, the resulting number is only the probability of the truth of a past or future event. If the butler killed the count with probability $A=0.75$, this means that in a quarter of the "parallel universes" he is not guilty. Should he be convicted in our universe?

---

Set of hypotheses

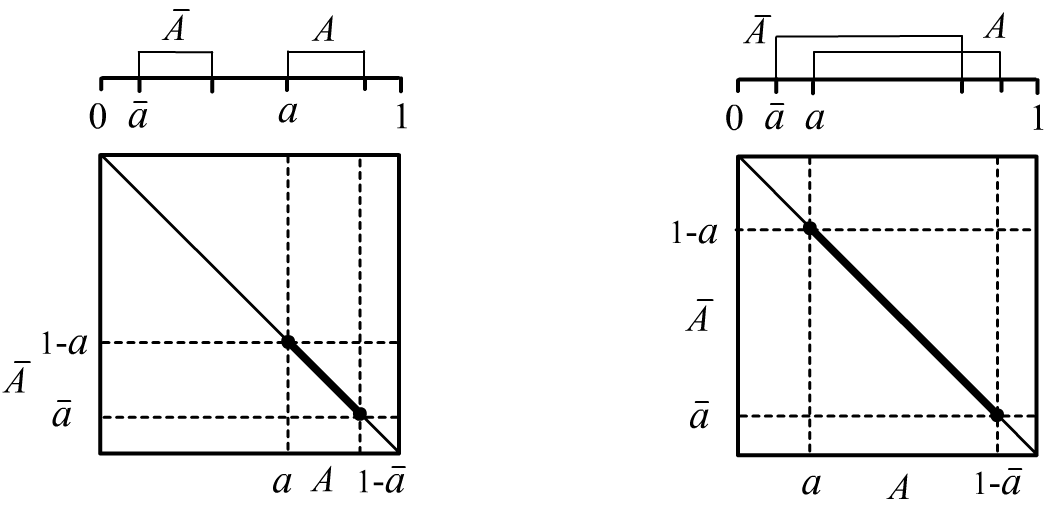
When considering a statement $A$ and its negation $\bar{A}$, we saw that their intervals cannot be arbitrary and are determined by two parameters ($a$, $\bar{a}$), rather than four. In the general case, let there be a set $\mathbb{H}=\{H_1,...,H_n\}$ of mutually exclusive events, $H_i\,\&\,H_j = 0$ for $i\neq j$ (hypotheses), which produce a partition of the sample space (in each trial exactly one of the $\mathbb{H}$ occurs). In this case: $$ H_1+...+H_n = 1,~~~~~~~~~~h_i \le H_i \le 1-\bar{h}_i,~~~~i=1...n $$ and the conditions for the consistency of the set of pairs $(h_i,\,\bar{h}_i)$ that define the interval bounds are more complex. One approach to satisfying these constraints was proposed in the Dempster–Shafer theory.

Let's describe another, simpler method.
Fix the lower bounds of the hypotheses $\mathbf{h}=\{h_1,...,h_n\}$ so that their sum does not exceed one. In vector notation, this sum can be expressed using the vector with unit components $\mathbf{t}=\{1,...,1\}$ (these are the coordinates of the vertex of the $n$-dimensional unit cube located "opposite" the origin): $$ \mathbf{h}\,\mathbf{t} ~=~ \sum^n_{i=1} h_i ~\le~ 1. $$ The vector of the "true" (but unknown) probabilities $H_i$ of the hypotheses satisfies the hyperplane equation $\mathbf{H}\mathbf{t}=1$. Since $\mathbf{t}^2=n$, it is easy to see that the point $$ \mathbf{h}' = \mathbf{h} + \frac{1-\mathbf{h}\,\mathbf{t}}{n}\,\mathbf{t} $$ also lies in this hyperplane ($\mathbf{h}'\mathbf{t}=1$). If we shift by the doubled vector $\mathbf{h}'-\mathbf{h}$, we end up on the opposite side of the hyperplane at the same distance (see the figure for $n=2$). This point determines the upper bounds of the truth-probability intervals of the hypotheses: $$ H_i = [h_i,~h_i+\frac{2}{n}\,(1-\mathbf{h}\,\mathbf{t})]. $$

As an example, consider $n=4$ hypotheses. Let $\mathbf{h}=\{0.0,~0.2,~0.2,~0.4\}$, then $\mathbf{h}\mathbf{t}=0.8$ and the consistent intervals of the hypotheses’ truth probabilities are: $$ H_1=[0.0,\,0.1],~~~H_2=[0.2,\,0.3],~~~H_3=[0.2,\,0.3],~~~H_4=[0.4,\,0.5]. $$

---

Conjunction, disjunction, and implication

Let the point probabilities of two events $A$ and $B$ be given, and suppose nothing else is known about them.
Then, in probability theory, the intervals for logical AND (conjunction) and logical OR (disjunction) are equal:

$$ \begin{array}{lccclcccccc} \max[0,~A+B-1]&\le& A\,\&\,B &\le& \min[A,\,B]\\[2mm] \max[A,\,B]&\le& A\vee B &\le&\min[1,~A+B] \end{array} $$

On the right is a graphical interpretation of these inequalities. For example, the maximum value of the intersection (conjunction) occurs when one event is a subset of the other. If the two event regions "fit" in the sample space without overlap, then the minimum intersection is zero. If their union "doesn’t fit," then the minimum intersection equals $P(A)+P(B)-1$.

---

In binary logic, implication $A\to B$ is false only for $\mathbb{T}\to \mathbb{F}$ (truth cannot imply falsehood) and is true in all other cases. It can also be expressed through disjunction and negation: $A\to B~~\equiv~~\bar{A} \vee B.$

	$W$	$\bar{W}$	Tot
$B$	8	2	10
$\bar{B}$	32	58	90
Tot	40	60	100

In probabilistic logic, implication can be interpreted as either the conditional probability $P(A\to B)$,
or the probability of the event $P(\bar{A} \vee B)$. In the general case $P(A\to B) \le P(\bar{A} \vee B)$. Therefore, choosing one or the other generally leads to different results. In the example of the smart blondes, for the rule

$B\to W$ : "if someone is blonde, then they are smart", we obtain: $P(B\to W)=0.8$ and $P(\bar{B} \vee W) = 0.98$. Intuitively, the first result seems more appropriate. From now on, we will assume that implication is expressed by conditional probability. As before, the probability symbol will be omitted, so $A\to B$ denotes either a number or, more generally, an interval within $[0...1]$.

From the definition $P(A\to B)=P(A,B)/P(A)$, when only the point probabilities of $A$, $B$ are known (and no additional information), we have $$ \max\bigr[0,~1-\frac{1-B}{A}\bigr]~~~~~~~\le~~~~A\to B~~~~\le~~~~~~\min\bigr[1,~B/A\bigr]. $$ The upper bound of this interval coincides with Goguen’s definition of implication in many-valued logic.

---

Interval relations

If only interval probabilities are known $A=[a,~1-\bar{a}]$, $B=[b,~1-\bar{b}]$ and no other information is available, then the intervals for conjunction and disjunction are as follows: $$ \begin{array}{lclclcccccc} A\,\&\,B &=& \bigr[ \max(0,~a+b-1) &,& 1-\max(\bar{a},\,\bar{b})\bigr]\\[2mm] A\vee B &=& \bigr[ \max(a,b) &,& 1-\max(0,~\bar{a}+\bar{b}-1)\bigr]\\[2mm] \end{array} $$

For the lower bound of the implication interval $P(A\to B)=P(A\,\&\,B)/P(B)$ we must take the minimum conjunction $A\,\&\,B$ and the maximum probability $A$. For the upper bound - the opposite (but not exceeding $1$): $$ \begin{array}{lclclcccccc} A\to B &=& \Bigr[ \max\Bigr(0,~\displaystyle\frac{a+b-1}{1-\bar{a}}\Bigr),~~~ 1- \max\Bigr(0,~ 1+\frac{\max(\bar{a},\,\bar{b})-1}{a}\Bigr)\Bigr]. \end{array} $$

The intervals for conjunction and disjunction can easily be obtained from the relations in the previous section. Some additional useful reasoning is also possible.

Suppose there exists a large number of equally probable elementary events $\mathbb{E}=\{E_1,...,E_n\}$.
Any event $A$ is a union of some part of elementary events (a subset of the set $\mathbb{E}$). We can represent it as a sequence $A=(01110?1??011)$ of length $n$, where a $1$ at position $i$ means $E_i\in A$, and $0$ means $E_i\not\in A$. The question mark denotes uncertainty (it is unknown whether $E_i\in A$ or $E_i\not\in A$). The number of known ones is $a\cdot n$, and the number of known zeros is $\bar{a}\cdot n$, so $A = [a,~1-\bar{a}]$.
If there are no question marks, then this is a point, unambiguous probability $a+\bar{a}=1$ (a coin). If the whole sequence consists only of question marks, then the probability $A=[0,\,1]$ is completely undefined (a cat in a room).

Let only $(\bar{a},a)$, $(\bar{b},b)$, be known for the events, while the order of the symbols $0,1,?$ in the sequences is unknown. The minimum value of their conjunction occurs when all $?=0$ (exactly $a\cdot n$ ones) and the ones of both sequences overlap as little as possible. The maximum value of the conjunction occurs when all $?=1$ (exactly $\bar{a}\cdot n$ zeros) and the sequences overlap on the ones as much as possible: $$ \min(A\,\&\,B) = \begin{array}{lclll} ~\overbrace{1...111}^{a}\,\overbrace{0...0}^{1-a}\\ ~\underbrace{0...0}_{1-b}\,\underbrace{1...111}_{b} \end{array} =\max(0,~a+b-1), ~~~~~~~~~~~~ \max(A\,\&\,B) = \begin{array}{lclll} ~\overbrace{1...11}^{1-\bar{a}}\,\overbrace{0...0}^{\bar{a}}\\ ~\underbrace{1...111}_{1-\bar{b}}\,\underbrace{0...0}_{\bar{b}} \end{array} =\min(1-\bar{a},\,1-\bar{b}). $$

Naturally, any meaningful information reduces the degree of uncertainty. For example, if it is known that the events are independent $P(A,B)=P(A)\,P(B)$, then $$ A\Prep B:~~~~~~~A\,\&\,B = [a\cdot b,~~~(1-\bar{a})\cdot(1-\bar{b})]. $$

Under the a priori assumption of equal probability for the arrangement of the symbols $0,1,?$ in the sequence, one can obtain the probability distribution of the "true value" $P(A)$ within the interval $A=[a,~1-\bar{a}]$.

---

Logical inference

In binary logic, $P$ logically implies $Q$, if, whenever formula $P$ is true, formula $Q$ is also true. This is denoted as: $P\Rightarrow Q$. Logical inference is a way of deriving some true formulas from other formulas that are also true. It is important not to confuse inference with implication $P\to Q$, which is a logical connective that takes values $0$ or $1$.

The rule of inference modus ponens: $A,~A\to B ~~\Rightarrow~~ B$ in Boolean logic this means: if statement $A$ is true, and from $A$ follows $B$ (implication), then one can conclude that statement $B$ is also true (and derivable).

In interval probabilistic logic, in addition to specifying the inference rule, one must also know the interval of truth for the derived formula. Suppose it is known that $A~=~[a,~1-\bar{a}]$ and $A\to B~=~[r,~1-\bar{r}]$ Using the identity of total probability, one can write: $$ P(A)\cdot P(A\to B) = P(A,B) ~~~~\le~~~ P(B)~~~~ \le~~~ 1. $$ On the other hand, $\min\bigr(A\cdot (A\to B)\bigr) ~=~ a\cdot r$, therefore, modus ponens takes the following form: $$ A~=~[a,~1-\bar{a}],~~~A\to B~=~[r,~1-\bar{r}]~~~~~~~~~~~\Rightarrow~~~~~~~~~~B~=~[a\cdot r,~1]. $$

If $r=1$, then $B=[a,~1]$. Graphically, this is an obvious result. If whenever event $A$ occurs, event $B$ also occurs, i.e. the conditional probability $P(A\to B)=1$. This means that event $A$ is a subset of event $B$. In the trial space the minimum possible area of $B$ cannot be smaller than the area of $A$ (see figure on the right).

---

---

Example: box and chest

Consider a world of rectangular closed boxes with the always true axiom

$(Y \lt X) ~\to~ \neg(X~\text{in}~Y)$: "if box $Y$ is smaller than box $X$, then box $X$ cannot be inside box $Y$". Assume there are two types of them — boxes and chests. Boxes are usually smaller than chests (although sometimes there are very small chests). It is also possible that boxes and chests are incomparable (for example, a tall and narrow box versus a wide and low chest). Therefore, let: $$ P(b \lt c) = 0.8,~~~~~~~~~~P(c \lt b) = 0.1. $$ Using modus ponens, we obtain: $$ \left\{ \begin{array}{lll} P(c~\neg\text{in}~b) ~=~ [0.8,~ 1] \\ P(b~\neg\text{in}~c) ~=~ [0.1,~1] \end{array} \right. ~~~~~~~\Rightarrow~~~~~~~ \left\{ \begin{array}{lll} P(c~\text{in}~b) ~=~[0,~ 0.2]\\ P(b~\text{in}~c) ~=~[0,~ 0.9] \end{array} \right. $$

Thus, the statement "the box is inside the chest" has an interval probability of $[0,~0.9]$. We have a small doubt ($\bar{a}=0.1=1-0.9$) that the box may be inside the chest. However, there is no supporting evidence for the hypothesis that it is actually there (it may or may not be). For the statement "the chest is inside the box", the probability restriction is much stricter.

---

Examples of inferences

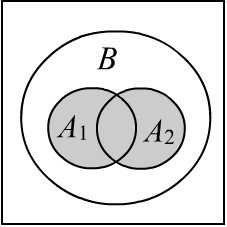Let there be two true rules $$ A_1\to B,~~~~~ A_2\to B $$ and probabilistic point premises $P(A_1),~P(A_2)$. Then (see figure): $$ \left\{ \begin{array}{lll} A_1\to B\\ A_2\to B\\ \end{array} \right. ~~~~~~~~~~~\Rightarrow~~~~~~~~~~P(A_1\vee A_2)~\le~ P(B)~\le~ 1. $$ In the case where the premises are independent, $B = [a_1+a_2-a_1a_2,~~1].$

---

Now consider two true rules $$ A_1\,\&\,\bar{A}_2\to B,~~~~~~~ A_2\,\&\,\bar{A}_1\to \bar{B}. $$ In Boolean logic, the premises cannot both be true simultaneously, otherwise a contradiction would be obtained: $B,\,\bar{B}$. This is accounted for in the conjunctions of the premises. In this case, we have: $$ b = \min B = \min(A_1\,\&\,\bar{A}_2),~~~~~~~~ \bar{b}~=~\min \bar{B} = \min(\bar{A}_1\,\&\,A_2). $$ If the statements $A_1, A_2$ are independent, then for $B$ we obtain an interval estimate: $[a_1\,(1-a_2),~1-(1-a_1)\,a_2]$, i.e. both bounds of the interval are nonzero.

---

If it is known that $A\to B$ and $B$ is true, then in classical logic one cannot, generally speaking, deduce $A$. Nevertheless, information about $B$ must somehow influence our conclusions. In probabilistic logic, this corresponds to the posterior adjustment of the probability of statement $A$ according to Bayes’ formula: $$ P(B\to A) = P(A\to B)\,P(A)/P(B). $$

---

---