ML: Dempster–Shafer Theory

Introduction

In Dempster–Shafer theory (DST), the truth measure of a statement $A$ is represented by an interval estimate $[a,~1-\bar{a}]$, where the lower bound $a$ is called belief and equals the sum of facts supporting the statement, and the upper bound, called plausibility, is equal to $1-$ the sum of facts contradicting statement $A$, i.e., supporting its negation $\bar{A}$. If there are no facts supporting the statement, then the lower bound (belief) is zero. If there are no facts contradicting the statement, then the upper bound (plausibility) is one. Such a situation, $[0,1]$, corresponds to complete uncertainty ("either I will meet a dinosaur, or I won’t").

The ability to distinguish between uncertainty $[0,1]$ and equal probability $[0.5,~0.5]$ is important for reasoning. For example, in the Bayesian method, if the prior probability of event $A$ is unknown, it is usually assumed that $P(A)=1/2$. The same choice must be made for "a truly equiprobable" event (such as a coin toss). Dempster–Shafer theory makes it possible to distinguish between these two situations.

Event truth interval

As an example, consider the statement "there is a box inside the chest" (the chest is closed).
There are two mutually exclusive hypotheses: $A$:"there is" and $\bar{A}$: "there is not." The truth intervals of these hypotheses may or may not overlap:

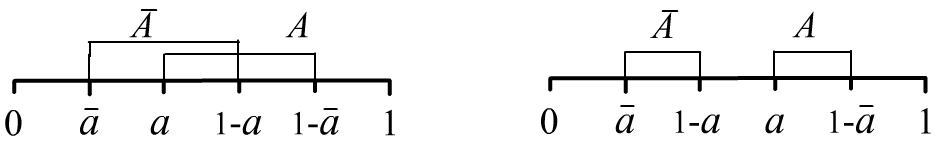
In the first illustration $a\lt 1/2$, in the second $a\gt 1/2$, and in both cases $\bar{a}\lt a$. Two more variants correspond to swapping $A$ and $\bar{A}$. When the intervals do not overlap and $a=1-\bar{a}$, we obtain the standard point probabilities $P(A)=a$ and $P(\bar{A})=\bar{a}$.

Since in the interval $A:~[\text{Bel}(A),~1-\text{Bel}(\bar{A})]=[a,\,1-\bar{a}]$ the upper bound must not be lower than the lower bound, the following constraint must hold: $$ \text{Bel}(A) + \text{Bel}(\bar{A}) \le 1. $$

For a large number of mutually exclusive statements $\{H_1,...,H_n\}$, tracking such inequalities to maintain consistency of the theory becomes nontrivial. The main task of Dempster–Shafer theory is precisely to construct a method for reconciling the interval bounds in evaluating the truth of different statements.

Mass functions

Let there be a set of mutually exclusive statements (hypotheses): $\mathbb{H}=\{H_1,...,H_n\}$, such that $H_i\,\&\,H_j = \mathbb{F}$ (false) for all $i\neq j$. In DST, such a set is called a frame of discernment or the universal set. In particular, the set $\mathbb{H}$ may consist of elementary events.

Now consider all the subsets of the set $\mathbb{H}$. They can be enumerated using $n$-digit binary numbers like $101...1$ (where hypothesis $H_1$ is included, hypothesis $H_2$ is not included, and so on). There will be $2^{|\mathbb{H}|}$ such numbers, where $|\mathbb{H}|=n$ is the number of elements in the set $\mathbb{H}$. The set of all subsets is denoted as $2^{\mathbb{H}}=\{\,A\mid A\subseteq \mathbb{H}\,\}$, where the symbol before the bar is an element, and the part after the bar specifies the condition it satisfies.

◊ For $\mathbb{H}=\{H_1,H_2,H_3\}$, there are eight subsets (including the empty set $\varnothing$ and $\mathbb{H}$ itself): $$ 2^{\mathbb{H}} ~=~ \{~ \varnothing,~\{H_1\},~\{H_2\},~\{H_3\},~\{H_1,H_2\},~\{H_1,H_3\},~\{H_2,H_3\},~\mathbb{H}~ \}. $$

Subsets are interpreted as the union of hypotheses using the logical exclusive OR: $H_1\oplus H_2$, i.e. $\{H_1,H_2\}$ means that either $H_1$ or $H_2$ (but not both) is true. The negation of a hypothesis $\bar{H}_1$ means that everything except it is true, i.e. $\{~\{H_2\},~\{H_3\},~\{H_2,H_3\}~\}$ (everything not containing $H_1$).

It is assumed that there are experts, each of whom may select one of the subsets as true. The proportion of experts who "voted" for a given subset $A\in 2^{\mathbb{H}}$ is called the mass of its support, denoted $m(A)$. We believe that each expert has made a choice, therefore: $$ m(\varnothing)=0,~~~~~~~~m(A) \ge 0,~~~~~~~~\sum_{A\,|\,A\,\in \,2^{\mathbb{H}}} m(A) = 1. $$ Instead of experts, one often speaks of the total (mass) of evidence supporting a given subset. Subsets for which $m(A) \gt 0$ are called focal elements, and their union is called the core.

◊ Suppose in the example with three hypotheses, the distribution of expert votes across subsets is as follows: $$ \begin{array}{r|l|l|l|l|l|l|l|l|} A: & \varnothing & \{H_1\} & \{H_2\} & \{H_3\} & \{H_1,H_2\} & \{H_1,H_3\} & \{H_2,H_3\} & \mathbb{H}\\ \hline m(A): & 0 & 0.1 & 0.4 & 0 & 0.2 & 0 & 0.3 & 0 \end{array} $$ Thus, not a single vote was cast for $H_3$, yet $30\%$ of experts believe that either $H_2$ or $H_3$ is true.
Moreover, $\mathbb{H}=\{H_1,H_2,H_3\}$ received no supporting votes at all. The focal elements are $\{H_1\}$, $\{H_2\}$, $\{H_1,H_2\}$, $\{H_2,H_3\}$, and their union (the core) coincides with $\mathbb{H}$.

Belief

A key concept in DST is the belief function of a subset $A$. It is denoted as $\text{Bel}(A)$ and is defined as the total mass of all subsets of hypotheses contained within $A$: $$ \text{Bel}(A) ~=~ \sum_{S\,\mid\, S\subseteq A} m(S) ~=~ m(A)~+~\sum_{S\,\mid\, S\subset A} m(S). $$

◊ Let’s calculate the belief values for some sets in the three-hypotheses example: $$ \begin{array}{lcll} \text{Bel}(H_1) &=& m(H_1) = 0.1,\\ \text{Bel}(H_1,H_2) &=& m(H_1) + m(H_2) + m(H_1,H_2) = 0.1+0.4 + 0.2 = 0.7, \\ \text{Bel}(H_1,H_3) &=& m(H_1) + m(H_3) + m(H_1,H_3) = 0.1+0 + 0 = 0.1, \\ \text{Bel}(H_1,H_2,H_3) &=& 1 \text{ (since one of them must be true)}. \end{array} $$

The belief in the entire set of hypotheses is always equal to one: $\text{Bel}(\mathbb{H})=1$, and the belief in a single hypothesis equals its mass $\text{Bel}(H_i)=m(H_i)$. It is easy to see that, knowing the beliefs of all subsets, one can reconstruct their masses: $$ m(\varnothing)=0,~~~~~~~~~m(A)~=~\text{Bel}(A) - \sum_{S\,\mid\, S\subset A} m(S) ~=~ \sum_{S\,\mid\, S\subseteq A} (-1)^{|A-S|}\,\text{Bel}(S). $$

Note that any subset $B\subset A$ represents a stronger (more specific) claim than $A$. Typically, it requires stronger evidence to support it. Nevertheless, even if $m(B)\gt m(A)$, the belief in $A$ will always be at least as high: $\text{Bel}(B)\le \text{Bel}(A)$.

Plausibility

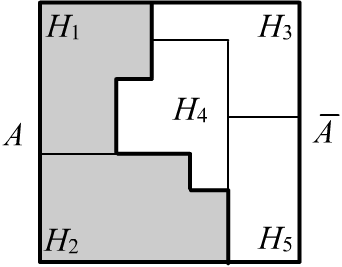Let the set $\mathbb{H}$ consist of five hypotheses, and the event (statement) be $A=\{H_1,H_2\}$.
Then its negation is $\bar{A}=\{H_3,H_4,H_5\}$. As a result, the event $A$ and its negation $\bar{A}$ split the hypothesis space $\mathbb{H}$ into two disjoint parts. Clearly, the belief in the negation $\bar{A}$ equals the sum of the masses of all subsets $2^{\mathbb{H}}$ that do not intersect with $A$: $$ \text{Bel}(\bar{A}) = \sum_{S\,\mid\,S\cap A = \varnothing} m(S). $$

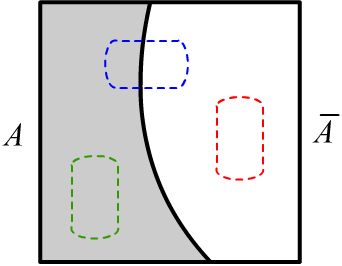The set $2^\mathbb{H}$ can be divided into three parts: all subsets $A$ (green in the figure): $\{S\,\mid\, S\subseteq A\}$; all subsets of its negation $\bar{A}$ (red): $\{S\,\mid\, S\subseteq \bar{A}\}$; and all subsets that intersect both $A$ and $\bar{A}$ (blue): $\{S\,\mid\,S\cap A\neq\varnothing \,\&\,S\cap \bar{A}\neq\varnothing \,\}$. The sum of their masses (which is the mass of the entire $2^\mathbb{H}$) equals one. Therefore, the degree of plausibility, defined as one minus the belief in the truth of the negation of $A$, can be expressed as: $$ \text{Pl}(A) ~=~ 1-\text{Bel}(\bar{A}) ~=~\sum_{S\,\mid\, S \cap A \neq \varnothing}m(S), $$ where the sum runs over the "blue" and "green" subsets, and $\text{Bel}(\bar{A})$ is the total mass of the "red" ones.

Since neither $\text{Bel}(A)$ nor $\text{Bel}(\bar{A})$ includes the "blue" subsets, whose masses in general may be nonzero, we conclude that the sum of the belief in a statement and the belief in its negation does not exceed one: $$ \text{Bel}(A)+\text{Bel}(\bar{A}) \le 1. $$ This is exactly what is required for any statement. For example, in the case of three hypotheses from the previous section, if $A=\{H_2\}$, then $\text{Bel}(\bar{A})=\text{Bel}(H_1,H_3)$ and $\text{Bel}(A)+\text{Bel}(\bar{A}) = 0.5$.

◊ Let’s calculate plausibility values in the three-hypotheses example: $$ \begin{array}{lcll} \text{Pl}(H_1) &=& m(H_1)+m(H_1,H_2)+m(H_1,H_3)+m(H_1,H_2,H_3) = 0.3,\\ \text{Pl}(H_1,H_2) &=& m(H_1) + m(H_2) + m(H_1,H_2) + m(H_1,H_3)+ m(H_2,H_3)+ m(H_1,H_2,H_3) = 1, \\ \text{Pl}(H_1,H_3) &=& m(H_1) + m(H_3) + m(H_1,H_2)+ m(H_1,H_3)+ m(H_2,H_3)+ m(H_1,H_2,H_3) = 0.6, \\ \text{Pl}(H_1,H_2,H_3) &=& 1. \end{array} $$

The probability $P(A)$ of the truth of statement $A$ lies within the interval: $ m(A)~\le~\text{Bel}(A)~\le~P(A)~\le~ \text{Pl}(A). $

Dempster’s rule

Often, information about the support (mass) of subsets comes from different independent sources and may be contradictory. Dempster’s Rule reconciles such information. Let there be two sets of mass functions $m_1(S)$ and $m_2(S)$ for all $S\subseteq \mathbb{H}$. They are combined into a unified mass system as follows: $$ m(A) = \frac{1}{\mathcal{N}}\,\sum_{S_1\cap S_2=A} m_1(S_1)\cdot m_2(S_2). $$ Here, all pairs of subsets $S_1,S_2 \subseteq \mathbb{H}$, whose intersection yields $A\neq\varnothing$ are considered. The combined mass $m(A)$ is proportional to the sum of products of the masses of such subsets. This relation is inspired by classical probability theory, where the probability of the joint occurrence of independent events is equal to the product of their probabilities.

The normalization coefficient $\mathcal{N}$ is calculated so that the total sum of $m(A)$ over all subsets of $\mathbb{H}$ equals one: $$ \mathcal{N} ~=~ \sum_{S\subseteq \mathbb{H}}\sum_{S_1\cap S_2=S} m_1(S_1)\cdot m_2(S_2) ~=~ \sum_{S_1\cap S_2\neq \varnothing} m_1(S_1)\cdot m_2(S_2). $$ The mass sets $m_1$ and $m_2$ are assumed to be normalized to one, therefore: $$ 1 = \sum_{S_1\subseteq \mathbb{H}}m_1(S_1) ~\sum_{S_2\subseteq \mathbb{H}}m_2(S_2) = \sum_{S_1,S_2\subseteq \mathbb{H}} m_1(S_1)m_2(S_2) = \sum_{S_1\cap S_2\neq \varnothing} m_1(S_1)\cdot m_2(S_2) ~~+ \sum_{S_1\cap S_2 = \varnothing} m_1(S_1)\cdot m_2(S_2), $$ where in the last equality all pairs of subsets $(S_1,S_2)$ are divided into intersecting and non-intersecting ones. As a result, the normalization coefficient can be written in a more convenient form for practical calculations: $$ \mathcal{N} ~=~ 1~~-\sum_{S_1\cap S_2 = \varnothing} m_1(S_1)\cdot m_2(S_2). $$ The value $\mathcal{N}$ is a measure of conflict between the sets $m_1(S)$ and $m_2(S)$, since it sums all non-intersecting subsets with $S_1\cap S_2=\varnothing$, which nevertheless received nonzero masses in each set (there are "votes" in their favor).

Finding the criminal

Let's consider an example borrowed from Yager, Liu (2008). Suppose there are three suspects in a bank robbery: Tony ($T$), Smith ($S$) and Dick ($D$). An elderly witness, Mrs. Johnson, saw a tall man near the bank at the time of the robbery. Her eyesight is not very good, so let us assume the reliability of her testimony is $60\%$. Since both Tony and Dick are tall, we have $m_1(T,\,D) = 0.6$. At the same time, since there are no other criminals in the city and Mrs. Johnson saw nothing else, we set $m_1(T,\,S,\,D) = 0.4$.

Another set of evidence is based on video surveillance. Although the robber was masked, the camera captured a blurry image of his eyes, which appeared black $4$ times more often than gray. Since Smith has black eyes, we assign $m_2(S)=0.8$ and $m_2 (T,\,D) = 0.2$.

$$ m(S) = \frac{1}{\mathcal{N}}\,m_1(T,\,S,\,D)\,m_2(S)=\frac{0.32}{\mathcal{N}},~~~~~~~~~\mathcal{N}=1-m_1(T,\,D)\,m_2(S)=1-0.48~~~~~~\Rightarrow~~~~~m(S)=0.62. $$ Similarly: $$ m(T,D) = \frac{0.12+0.08}{1-0.48}=0.38. $$

Let's present the belief intervals for the suspects, according to each source of evidence and their combination: $$ \begin{array}{ccccc} ~ & \text{Mrs. Johnson} & \text{Video surveillance} & \text{Combination} \\ \hline T & [0.0,\,1.0] & [0.0,\,0.2] & [0.00,\,0.62] \\ S & [0.0,\,0.4] & [0.8,\,0.8] & [0.62,\,0.62] \\ D & [0.0,\,1.0] & [0.0,\,0.2] & [0.00,\,0.62] \end{array} $$

It should be noted that Dempster’s rule can lead to strange results in highly conflicting situations. Suppose, for example, there are three suspects $T,D,S$ and two witnesses $W_1$ and $W_2$, who make the following statements: $$ \begin{array}{lll} W1:& m(T)=0.9 & m(D)=0.1\\ W2:& m(S)=0.9 & m(D)=0.1\\ \end{array} $$ Applying Dempster’s rule gives $\mathcal{N}=0.99$ and $m(D)=1$, even though both witnesses assigned only small masses to the hypothesis $m(D)$.

Classification algorithm

In the work of Chena et al. (2014), a classification algorithm was proposed based on Dempster’s rule. As the frame of discernment $\mathbb{H}$, the hypotheses $H_k$ represent the object’s membership in the $k$-th class.

In the simplest case of two classes, $\mathbb{H}=\{H_1,H_2\}$, the algorithm works as follows. For each feature (individually), mass functions are constructed in the form of sigmoids $m_i(H_1)=1/(1+e^{v_i-t_i})$, $m(H_2)=1-m(H_1)$, where $v_i$ is the value of the $i$-th feature, and $t_i$ is the threshold (a training parameter). Then, the mass functions of the features are multiplied (Dempster’s rule) and normalized.. The resulting mass function is used as a classifier: if $m(H_1) \gt m(H_2)$, then class $H_1$ is chosen.

There is a Python implementation of this algorithm.

References