ML: Some problems in probability theory
The Wumpus World
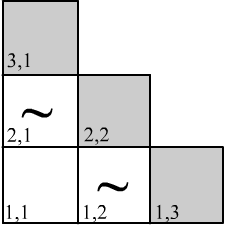Let's consider a good example of decision-making in the model world of the Wumpus.
This world consists of cells through which an intelligent agent moves.
Let each cell independently have a probability of $P(h)=0.2$ of containing a hole.
In this case, in each of the four neighboring cells with a hole, there will definitely be a breeze.
Suppose the agent has explored three corner cells of its world. There are no holes in them,
but two of them have a breeze (tilde in the figure on the right). It is necessary to determine the probabilities of holes in the cells (gray color)
adjacent to the explored area.
Let's denote the known information about holes and breeze as two sets: $\mathbb{H}=\{\bar{h}_{11},\,\bar{h}_{12},\,\bar{h}_{21}\}$ (no holes) and $\mathbb{B}=\{\bar{b}_{11},\,b_{12},\,b_{21}\}$ (there is no breeze in cell $[1,1]$, but there is a breeze in $[1,2]$ and $[2,1]$). We want to compute, for example, the probability of a hole in the upper cell of border $H_{3,1}:\,\{h_{3,1},\,\bar{h}_{3,1}\}$, where the value $h_{3,1}$ of the random variable $H_{3,1}$ means that there is a hole, and the value $\bar{h}_{3,1}$ means that there is none: $$ P(\mathbb{H}, \mathbb{B}\to H_{31}) ~\sim~ P(H_{31},\mathbb{H},\mathbb{B}) = \sum_{H_{22},H_{13}} P(H_{31}, H_{22},H_{13}, \mathbb{H},\mathbb{B}). $$ Above, the symbol "$\sim$" means that we omit the factor independent of the variable $H_{1,3}$, which is by definition the conditional probability $P(\mathbb{H}, \mathbb{B})$. Then we expand the joint probability to neighboring cells using the law of total probability. The sum consists of four terms for all possible values $H_{2,2}:\,\{h_{2,2},\,\bar{h}_{2,2}\}$ и $H_{1,3}:\,\{h_{1,3},\,\bar{h}_{1,3}\}$. Utilizing again the definition of conditional probability and the independence of $H_{ij}$, we have: $$ P(\mathbb{H}, \mathbb{B}\to H_{31}) ~\sim~ \sum_{H_{22},H_{13}} \, P(H_{31})P(H_{22})P(H_{13})\, P(H_{31}, H_{22},H_{13}, \mathbb{H}\to \mathbb{B}). $$ The joint probability was extended to the entire border, as the probability of breeze presence (the information available to the agent $\mathbb{B}$) depends on the presence or absence of holes in all cells shown in the figure. Now we can proceed with the calculations, explicitly expanding the sums: $$ \begin{array}{lcl} P(\mathbb{H}, \mathbb{B}\to h_{31}) &\sim& \, P(h_{31})P(h_{22})P(h_{13})\,P(h_{31}, h_{22},h_{13}, \mathbb{H}\to \mathbb{B})~+~P(h_{31})P(\bar{h}_{22})P(h_{13})\,P(h_{31}, \bar{h}_{22},h_{13}, \mathbb{H}\to \mathbb{B})\\ & +& \, P(h_{31})P(h_{22})P(\bar{h}_{13})\,P(h_{31}, h_{22},\bar{h}_{13}, \mathbb{H}\to \mathbb{B})~+~\, P(h_{31})P(\bar{h}_{22})P(\bar{h}_{13})\,P(h_{31}, \bar{h}_{22},\bar{h}_{13}, \mathbb{H}\to \mathbb{B}), \\ P(\mathbb{H}, \mathbb{B}\to \bar{h}_{31}) &\sim& \, P(\bar{h}_{31})P(h_{22})P(h_{13})\,P(\bar{h}_{31}, h_{22},h_{13}, \mathbb{H}\to \mathbb{B})~+~P(\bar{h}_{31})P(\bar{h}_{22})P(h_{13})\,P(\bar{h}_{31}, \bar{h}_{22},h_{13}, \mathbb{H}\to \mathbb{B})\\ & +& \,P(\bar{h}_{31})P(h_{22})P(\bar{h}_{13})\,P(\bar{h}_{31}, h_{22},\bar{h}_{13}, \mathbb{H}\to \mathbb{B})~+~ P(\bar{h}_{31})P(\bar{h}_{22})P(\bar{h}_{13})\,P(\bar{h}_{31}, \bar{h}_{22},\bar{h}_{13}, \mathbb{H}\to \mathbb{B}). \\ \end{array} $$ Let's consider that $P(h_{ij})=0.2$ and $P(\bar{h}_{ij})=0.8$. The probability $P(h_{31}, h_{22},h_{13}, \mathbb{H}\to \mathbb{B})=1$ since there are holes on the border everywhere, which inevitably leads to breeze, while $P(h_{31}, \bar{h}_{22},\bar{h}_{13}, \mathbb{H}\to \mathbb{B})=0$ as the absence of holes in cells $[2,2]$ and $[1,3]$ contradicts the presence of breeze in $[1,2]$. Similarly in other cases: $$ \begin{array}{lcl} P(\mathbb{H}, \mathbb{B} \to h_{31} ) &\sim& 0.2^3 + 0.2^2\,0.8 + 0.2^2\,0.8, \\ P(\mathbb{H}, \mathbb{B} \to \bar{h}_{31} ) &\sim& 0.2^2\,0.8 + 0.2\,0.8^2. \end{array} $$ This result can be represented as a vector, with two components: $$ P(\mathbb{H}, \mathbb{B}\to H_{31})~\sim \bigr\{0.2^3 + 2\cdot 0.2^2\cdot 0.8,~~~ 0.2^2\cdot 0.8 + 0.2\cdot 0.8^2\bigr \} \sim \bigr\{1 + 2\cdot 4,~~~ 4 + 4\cdot 4\bigr \}. $$ Now it needs to be normalized to unity (restoring the omitted factors): $$ P(\mathbb{H}, \mathbb{B}\to H_{31}) = \bigr\{9,~ 20\bigr \}/(9+20) = \bigr\{0.31,~ 0.69 \}. $$ Thus, the probability of finding a hole in cell $[3,1]$ is $0.31$. It is worth checking similarly that the probability of a hole in a cell $[2,2]$ is $0.86$. Therefore, the agent should (if necessary) move either to cell $[3,1]$, or to cell $[1,3]$.
Shen's unfair game
Two players toss a coin with sides marked $0$ and $1$, resulting in a sequence like $00110101...$. Before the game begins, the first player chooses and announces any three-digit sequence, for example, $001$. Then, the second player selects their own sequence of the same length. The winner is the one whose sequence appears first. This game is an example of a random process with terminal states.
Since the first player has the opportunity to choose the optimal combination, at first glance, they seem to have an advantage in this game. However, this is not the case, and the second player has significantly greater chances of winning!
Let's say the first player chose $001$. What combination should the second player choose? Obviously, they should select one that blocks the winning combination of the first player as much as possible. Before the potential victory of the first player $001$, there may be such scenarios: $...\underline{000}1$ or $...\underline{100}1$. Therefore, the second player should choose $000$ or $100$. The option $000$ is worse because it "blocks" itself. Let's consider the option $100$.
On the first graph above, all transitions for the random process are shown, where the state is determined by the last three values. For example, let the last three results of the coin toss be $...000$ (three heads). The next toss will equally likely yield two new sequences $...000$ (a loop at the node) or $...001$. In the second figure the graph splits into two subgraphs due to the presence of terminal nodes (red, where the first player wins, and blue, where the second player wins). Arrows do not exit these nodes (end of the game). There are $6$ equiprobable nodes leading to the second player's winning node (including this node obtained after the first three tosses). Therefore, the probability of the second player winning is $6/8=3/4$.
The same result can be obtained using the following calculations. Let's denote the conditional probability of the second player winning as $p_{00}$, if the last two digits of the sequence are $00$. After that, $0$ or $1$ can equally likely follow, leading to $000$ or $001$. In the first case, we again get $p_{00}$, and in the second case, the second player loses. Similar reasoning applies to the other four cases: $$ p_{00}=\frac{1}{2}\,p_{00}+\frac{1}{2}\,0,~~~~~~~~~~~~ p_{01}=\frac{1}{2}\,p_{10}+\frac{1}{2}\,p_{11},~~~~~~~~~~~~ p_{10}=\frac{1}{2}\,1+\frac{1}{2}\,p_{01},~~~~~~~~~~ p_{11}=\frac{1}{2}\,p_{10}+\frac{1}{2}\,p_{11}. $$ Solving this system, we obtain $p_{00}=0$, $p_{10}=p_{01}=p_{11}=1$. Since all backstory variants are equally probable, the probability of the second player winning is $(0+1+1+1)/4=3/4$.
| 000 | 001 | 100 | 010 | 101 | 011 | 110 | 111 |
| 100 | 100 | 110 | 001 | 110 | 001 | 011 | 011 |
| 7/8 | 3/4 | 2/3 | 2/3 | 2/3 | 2/3 | 3/4 | 7/8 |
It is worth noting that four combinations $000$, $010$, $101$, $111$ are disadvantageous for the second player in any case. The transition graphs split, giving the maximum probability of winning, only in four out of eight cases. In the remaining four cases, the advantage of the second player is also easy to see:
On the first graph, the red node $010$ (for the first player) can be reached from 4 nodes ($101$, $011$, $111$, $110$), while the blue node (for the second player) can be reached from six nodes.
