ML: Линейная модель
Введение
В этом документе рассматривается многомерная линейная модель. Она имеет самостоятельное значение в некоторых задачах машинного обучения и лежит в основе сложных архитектур глубоких нейронных сетей. Обсуждаются математические формулировки модели и аналитический поиск её параметров. Приведены примеры кода на Python которые можно найти в файле: ML_Line_Model.ipynb.
Рассмотрим $n_x$-мерное пространство признаков. Каждый объект в этом пространстве описывается вектором $\mathbf{x}$. Задача состоит в преобразовании исходного пространства признаков в другое, $n_y$-мерное пространство $\mathbf{y}$. Величины $\mathbf{y}$, сами по себе, могут иметь практический смысл и тогда это регрессия или быть новыми признаками объектов, определяющими вероятности в задаче классификации.
Линейная модель является простейшей связью входа $\mathbf{x}$ и выхода $\mathbf{y}$. Её матричная и индексная записи имеют вид:
$$ \mathbf{y} = \mathbf{b} + \mathbf{x}\cdot\mathbf{w}, ~~~~~~~~~~~~~~~~~~~~ y_\alpha = b_\alpha + \sum_\beta (x_\beta\, w_{\beta\alpha}) $$В процессе обучения необходимо подобрать оптимальные параметры модели: матрицу вектор $b_\beta$ и $w_{\alpha\beta}$. Линейная модель является первым нетривиальным приближением разложения в ряд Тейлора произвольной функции $\mathbf{y}=f(\mathbf{x}\, \boldsymbol{\omega})$.
Линейная модель как гиперплоскость
Рассмотрим геометрическую интерпретацию линейной модели.
В $n$-мерном пространстве каждая точка описывается $n$ вещественными координатами $\mathbf{x}=\{x_1,...,x_n\}$.
Как и в обычном 3-мерном пространстве, плоскость задаётся вектором нормали
$\boldsymbol{\omega}=\{w_1,...,w_n\}$ (перпендикуляр к плоскости)
и произвольной точкой
$\mathbf{x}_0=\{x_{01},...,x_{0n}\}$,
лежащей в этой плоскости (фиксирующей смещение плоскости вдоль нормали).
Когда $n > 3$ плоскость принято называть гиперплоскостью.
Расстояние $d$ от гиперплоскости до некоторой точки $\mathbf{x}=\{x_1,...,x_n\}$ вычисляется по формуле ($\boldsymbol{\omega}^2=1$):
$$ d = b+\mathbf{x}\cdot\boldsymbol{\omega}, ~~~~~~\text{где}~~~~~~~~~~ b ~=~ -\mathbf{x}_0\cdot\boldsymbol{\omega} ~=~ -( x_{01}w_1 + ... + x_{0n}w_{n} ). $$При этом $d > 0$, если точка $\mathbf{x}$ лежит с той стороны гиперплоскости, куда указывает вектор $\boldsymbol{\omega}$ и $d < 0$, если с противоположной. Когда $d=0$ - точка $\mathbf{x}$ лежит в гиперплоскости ($b+\mathbf{x}\cdot\boldsymbol{\omega} = 0$ - её уравнение).
Изменение параметра $b$ сдвигает плоскость параллельным образом в пространстве. Если $b$ уменьшается, то плоскость смещается в направлении вектора $\boldsymbol{\omega}$ (расстояние $d$ меньше), а если $b$ увеличивается - плоскость смещается против вектора $\boldsymbol{\omega}$. Это непосредственно следует из приведенной выше формулы.
◄
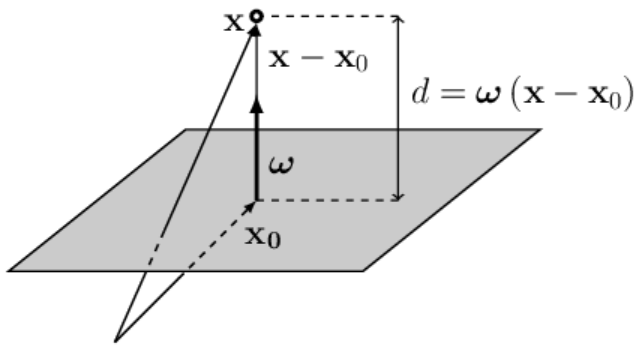Запишем вектор $\mathbf{x}-\mathbf{x}_0$, начинающийся в точке $\mathbf{x}_0$
(лежащей в плоскости)
и направленный в точку $\mathbf{x}$ (см. рисунок справа; векторы складываются по правилу треугольника).
Положение точки $\mathbf{x}_0$ выбрано в основании вектора $\boldsymbol{\omega}$,
поэтому $\boldsymbol{\omega}$ и $\mathbf{x}-\mathbf{x}_0$ коллинеарны (лежат на одной прямой).
Если вектор $\boldsymbol{\omega}$ единичный ($\boldsymbol{\omega}^2=1$), то скалярное произведение векторов
$\mathbf{x}-\mathbf{x}_0$ и $\boldsymbol{\omega}$ равно расстоянию точки $\mathbf{x}$ до плоскости:
$$
d = (\mathbf{x}-\mathbf{x}_0)\cdot \boldsymbol{\omega} ~=~ -\mathbf{x}_0\cdot\boldsymbol{\omega} + \mathbf{x}\cdot\boldsymbol{\omega}
~=~ b + \mathbf{x}\cdot\boldsymbol{\omega}.
$$
Если длина $\omega=|\boldsymbol{\omega}|$ вектора $\boldsymbol{\omega}$ нормали к гиперплоскости отлична от единицы, то $d$ в $\omega$ раз больше ($\omega > 1$) или меньше ($\omega < 1$) евклидового расстояния в $n$-мерном пространстве. Когда векторы $\mathbf{x}-\mathbf{x}_0$ и $\boldsymbol{\omega}$ направлены в противоположные стороны: $d < 0$. ►
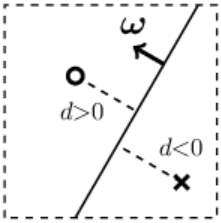Если пространство имеет $n$ измерений,
то гиперплоскость это $(n-1)$-мерный объект.
Она делит всё пространство на две
части.
Для наглядности рассмотрим 2-мерное пространство.
Гиперплоскостью в нём будет прямая линия (одномерный объект).
Справа на рисунке кружок изображает одну точку пространства,
а крестик - другую. Они расположены по разные стороны от линии (гиперплоскости).
Если длина вектора $\boldsymbol{\omega}$ много больше единицы, то и расстояния
$d$
от точек к плоскости по модулю будут существенно большими единицы.
Регрессии (предсказание вещественного числа)
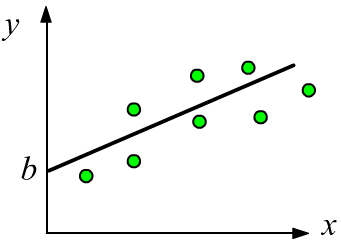Простейшим примером регрессии является одномерная линейная функция $y = b + w \,x$,
в которой параметр $w$ характеризует наклон прямой, а параметр $b$ - сдвиг (смещениие) по оси $y$ от начала координат.
Наличие подобной связи между $x$ и $y$, обычно, легко обнаружить визуально на графике даннных.
В многомерном случае $y=b + w_1x_1+...w_n x_n$ визуализировать данные сложнее. Чтобы убедится в адекватности линейной модели, необходимо найти оптимальные параметры и вычислить величину ошибки (сравнив её с ошибками других моделей, в т.ч. с тривиальной $y=b=\text{const}$).
Логистическая регрессия (задача классификации)
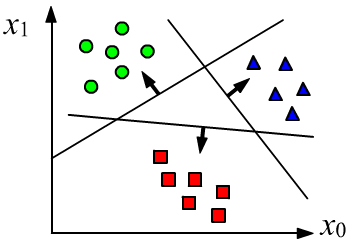В задаче классификации объект $\mathbf{x}$ необходимо отнести к одному или нескольким
классам, общее число $C$ которых фиксированно.
Обычно, результатом классификации является $C$ условных вероятностей $p(c|\mathbf{x})$ того,
что объект с признаками $\mathbf{x}$ принадлежит $c$-тому классу: $c\in [0...C-1]$.
При использовании в задаче классификации линейной модели, её выходы $y_\alpha$ "пропускают" через нелинейную функцию $z_\alpha=f(y_\alpha)$, значения которой находятся в диапазоне $[0...1]$. Чем ближе $z_\alpha$ к единице, тем увереннее модель относит объект к классу с номером $\alpha$.
$$ z_{\alpha} ~=~f(\mathbf{y}) ~=~f\Bigr(b_\alpha + \sum_{\mu} x_{\mu}\, w_{\mu \alpha} \Bigr) $$Если объект может принадлежать к нескольким классам (классы пересекаются), то в качестве $f(z)$ удобна сигмоидная функция. Если на нескольких выходах модели получаются значения близкие к единице, то объект принадлежит всем этим классам. При больших $y_\alpha$ сигмоид стремиться к единице, а при $y_\alpha\to -\infty$ - к нулю: $\sigma(y_\alpha) = 1/(1+e^{-y_\alpha})$
Для непересекающихся классов $C > 2$ (объект $\mathbf{x}$ принадлежит только одному классу), обычно, применяют функцию softmax. На её выходе получаются положительные значения, сумма которых равна единице. Поэтому их можно интерпретировать как распределение вероятностей $p(c|\mathbf{x})$: $$ z_\alpha = \mathrm{sm}(y_\alpha) = \displaystyle \frac{e^{y_\alpha}}{\sum_\beta e^{y_\beta}},~~~~~~~~~~~~~~~~~~~~~\sum_\alpha z_\alpha = 1,~~~~~~~~~z_\alpha > 0. $$
Если разделяющие плоскости для $\{y_0,y_1,y_2\}$ проведены верно и классы линейно разделимы, то для точки, относящейся к классу $0$, значения выходов будут стремиться к $\{1,0,0\}$, для класса $1$ - $\{0,1,0\}$ и т.д.
Формула Байеса и софтмакс
Существует замечательный математический факт, который подводит "теоретическую основу" под использование функции софтмакса. Пусть примеры каждого класса $c=[0...,C-1]$ в пространстве признаков $\mathbf{x}$ образуют "кластеры" с нормальными распределениями, которые имеют одинаковую дисперсию $\mathbf{D}$ и различные средние $\bar{\mathbf{x}}_c$. Тогда условная вероятность $p(c|\mathbf{x})$ принадлежности объекта с признаками $\mathbf{x}$ к классу $c$, описывается линейной моделью с софтмакс-функцией на выходе: $$ P(\mathbf{x} | c) \sim e^{-\frac{1}{2}\,(\mathbf{x}-\bar{\mathbf{x}}_c)\,\mathbf{D}^{-1}(\mathbf{x}-\bar{\mathbf{x}}_c)}~~~~~~~~~~~~~ \Rightarrow~~~~~~~~~~~~~ p(c|\mathbf{x}) = \frac{e^{y_c}}{\sum_\alpha e^{y_\alpha}},~~~~~~~\mathbf{y} = \mathbf{b} + \mathbf{x}\mathbf{w}. $$
Естественно, в реальных задачах классы в пространстве признаков редко удовлетворяют исходной посылке. Однако, при помощи нейронных сетей, часто удаётся построить подходящее нелинейное преобразование, дающее новое пространство признаков. В этом пространстве объекты, принадлежащие различным классам, образуют линейно разделимые, компактные кластеры классов. Ниже идёт идея доказательства, которое можно пропустить.🔥 Из определения условной вероятности следует формула Байеса: $$ p(c|\mathbf{x}) = \frac{p(c,\mathbf{x})}{p(\mathbf{x})} = \frac{p(c)\,P(\mathbf{x}|c)}{p(\mathbf{x})} = \frac{p(c)\,P(\mathbf{x}|c)}{\sum_\alpha p(\alpha)\,P(\mathbf{x}|\alpha)}, $$ где $p(c)$ - вероятности принадлежности случайно выбранного объекта к классу $c$. Распишем произведение $(\mathbf{x}-\bar{\mathbf{x}}_c)\,\mathbf{D}^{-1}(\mathbf{x}-\bar{\mathbf{x}}_c)$ под экспонентой в $P(\mathbf{x} | c)$. Слагаемое $-(1/2)\,\mathbf{x}\,\mathbf{D}^{-1}\mathbf{x}$, присутствующее и в числителе, и в знаменателе формулы Байеса сокращается. Остальные слагаемые и множитель $p(c)$ можно факторизовать следующим образом (обратная матрица дисперсии $\mathbf{D}^{-1}$ симметрична): $$ p(c)\,P(\mathbf{x}|c) \sim e^{b_c + \mathbf{x}\,\mathbf{w}_c},~~~~~~~~~ b_c = -\frac{1}{2}\,\bar{\mathbf{x}}_c\,\mathbf{D}^{-1}\bar{\mathbf{x}}_c + \log\, p(c),~~~~~~~~~~ \mathbf{w}_c = \mathbf{D}^{-1}\bar{\mathbf{x}}_c. $$
Батчи и перемножение матриц
Пусть есть 2 признака: $\{x_0,x_1\}$ (вход модели), которые определяют три целевых величины: $\{y_0,y_1,y_2\}$ (выход). Линейную связь между выходом и входом: $$ \left\{\begin{array}{lcl} y_0 &=& b_0+ x_0 \,w_{00} + x_1\, w_{10} \\ y_1 &=& b_1+ x_0 \,w_{01} + x_1\, w_{11} \\ y_2 &=& b_2+ x_0 \,w_{02} + x_1\, w_{12} \end{array} \right. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \mathbf{w} = \overbrace{ \begin{array}{|c|c|c|} \hline w_{00} & w_{01} & w_{02} \\ \hline w_{10} & w_{11} & w_{12} \\ \hline \end{array} }^{\displaystyle n_y} \left. \phantom{ \begin{array}{c} \\ \\ \end{array} } \right\} n_x $$ можно записать в табличном виде (точка - это dot-умножение строки на столбец):
$$ \begin{array}{|c|c|} \hline b_{0} & b_{1} & b_{2} \\ \hline \end{array} ~~~+~~~ \begin{array}{|c|c|} \hline x_0 & x_1 \\ \hline \end{array} ~\cdot~ \begin{array}{|c|c|c|} \hline w_{00} & w_{01} & w_{02} \\ \hline w_{10} & w_{11} & w_{12} \\ \hline \end{array} ~~~=~~~ \begin{array}{|c|c|} \hline y_{0} & y_{1} & y_{2} \\ \hline \end{array} $$
В алгоритмах машинного обучения вычисление происходит не с одним примером,
а сразу с некоторым их множеством - пачкой (batch).
Поэтому представим $\mathbf{x}$ в виде 2D матрицы,
расположив примеры построчно (первый индекс, начиная с нуля - номер примера, а второй - номер признака в данном примере).
Ниже приведено $N=4$ примера, $n_x=2$ признака и $n_y=3$ выходов модели:
Размерности индексов (атрибут shape в numpy)
матрицы произведения $\mathbf{x}\cdot\mathbf{w}$ равны:
$$
(N,n_x) . (n_x,n_y) = (N,n_y).
$$
При свёртке матриц:
$(\mathbf{x}\cdot\mathbf{w})_{i\alpha} = \sum_\mu x_{i\mu}\,w_{\mu\alpha}$
действует принцип "строка на столбец"
и размерность среднего индекса сокращается.
К каждой строке матрицы $\mathbf{x}\cdot\mathbf{w}$ формы (N,ny)
добавляется вектор $\mathbf{b}$ формы (ny,).
В библиотеке numpy это соответствует правилу расширения
(broadcasting).
Тензорный анализ
Далее будут вычисляться производные по тензорам и использоваться матричные оозначения. Поэтому напомним некоторые важные моменты.
☝ Матрица, обратная к матрице $\mathbf{A}$, обозначается как $\mathbf{A}^{-1}$, а транспонированная как $\mathbf{A}^{\top}$. У транспонированной матрицы колонки и строки (индексы) переставлены местами: $A^\top_{ij}=A_{ji}$, а произведение обратной на исходную даёт единичную матрицу (символ Кронекера). Они обладают следующими свойствами: $$ \mathbf{A}^{-1}\cdot\mathbf{A}=\mathbf{A}\cdot\mathbf{A}^{-1}=\mathbf{1},~~~~~~~~~~ (\mathbf{A}\cdot\mathbf{B})^{-1} = \mathbf{B}^{-1}\cdot\mathbf{A}^{-1},~~~~~~~~~~ (\mathbf{A}\cdot\mathbf{B})^{\top} = \mathbf{B}^{\top}\cdot\mathbf{A}^{\top}. $$
☝ Справедлива формула для частной производной (многоточие - это другие индексы):
$$ \frac{\partial W_{\mu\nu...}}{\partial W_{\alpha\beta...}} = \delta_{\mu\alpha}\,\delta_{\nu\beta}\,...,~~~~~~~~~~~~~~ \sum_{\mu} T_{...\mu...}\,\delta_{\mu\alpha} = T_{...\alpha...}, $$где $\delta_{\alpha\beta}$ - единичная квадратная матрица (символ Кронекера), равная $0$, если $\alpha\neq\beta$ и $1$, если $\alpha=\beta$. При суммировании с символом Кронекера (по одному из его индексов), сумма и символ Кронекера убираются, а суммационный индекс заменяется на второй индекс символа Кронекера (выше вторая формула).
Формула для $\partial W_{\mu\nu}/\partial W_{\alpha\beta}$, означает, что производная равна нулю, если $\mu\neq\alpha$ и $\nu\neq\beta$. Например, $\partial W_{12}/\partial W_{13} = 0$ так это разные переменные (типа $\partial y/\partial x = 0$), а $\partial W_{12}/\partial W_{12} = 1$ (типа $\partial x/\partial x = 1$).
Аналитическое решение
В линейной модели с mse-ошибкой аналитически несложно найти оптимальные параметры. Вычисления оказываются заметно проще, если вектор $\mathbf{b}$ и матрицу $\mathbf{w}$ объединить в одну матрицу $\mathbf{W}$, добавив в $\mathbf{w}$, в качестве ещё одной строки, вектор $\mathbf{b}$. Дополнительно в матрицу $\mathbf{x}$ добавляется колонка, состоящая из единиц, что даёт матрицу $\mathbf{X}$:
$$ \mathbf{X}\cdot\mathbf{W} ~=~ \begin{array}{|c|c|c|} \hline x_{00} & x_{01} & ~1~ \\ \hline x_{10} & x_{11} & 1 \\ \hline x_{20} & x_{21} & 1 \\ \hline x_{30} & x_{31} & 1 \\ \hline \end{array} ~\cdot~ \begin{array}{|c|c|} \hline w_{00} & w_{01} & w_{02} \\ \hline w_{10} & w_{11} & w_{12} \\ \hline b_{0} & b_{1} & b_{2} \\ \hline \end{array} ~=~ \begin{array}{|c|c|c|} \hline y_{00} & y_{01} & y_{02} \\ \hline y_{10} & y_{11} & y_{12} \\ \hline y_{20} & y_{21} & y_{22} \\ \hline y_{30} & y_{31} & y_{32} \\ \hline \end{array} ~=~ \mathbf{y}. $$ Такая запись означает введение ещё одного фиктивного признака всегда равного единице: $\mathbf{x}=\{x_0,...,x_{n-1},1\}$.Теперь модель имеет вид: $\mathbf{y} = \mathbf{X}\cdot\mathbf{W}$, что, как несложно проверить, эквивалентно исходной записи $\mathbf{y}=\mathbf{b} + \mathbf{x}\mathbf{w}$. Найдём минимум mse-ошибки $L$ (опускаем постоянный множитель):
$$ L = \sum_{i,\nu} (y_{i\nu} -\hat{y}_{i\nu} )^2,~~~~~~~~~~~~~~~ y_{i\nu} = \sum_{\mu} X_{i\mu} W_{\mu\nu}. $$Запишем производные ошибки и выхода модели: $$ \frac{\partial L}{\partial y_{i\nu}}~=~ 2(y_{i\nu} -\hat{y}_{i\nu} ),~~~~~~~~ \frac{\partial y_{i\nu}}{\partial W_{\alpha\beta}} = \sum_{\mu} X_{i\mu}\,\delta_{\mu\alpha}\,\delta_{\nu\beta}. ~=~X_{i\alpha} \,\delta_{\nu\beta}. $$ Теперь несложно найти производную ошибки $L$ по элементам матрицы $W_{\alpha\beta}$: $$ \frac{\partial L}{\partial W_{\alpha\beta}} = \sum_{i,\nu} \frac{\partial L}{\partial y_{i\nu}}\,\frac{\partial y_{i\nu}}{\partial W_{\alpha\beta}} ~=~ 2 \sum_{i} (y_{i\beta} -\hat{y}_{i\beta} )\, X_{i\alpha} ~=~2 \bigr[\mathbf{X}^\top\cdot(\mathbf{y}-\hat{\mathbf{y}} )\bigr]_{\alpha\beta}. $$
Приравняв производную нулю (условие экстремума и в данном случае минимума $L$), получаем матричное уравнение $\mathbf{X}^\top\cdot(\mathbf{X}\cdot\mathbf{W}-\hat{\mathbf{y}} ) = 0$, которое легко решается:
$$ \mathbf{W} = (\mathbf{X}^\top\cdot \mathbf{X})^{-1}\cdot (\mathbf{X}^\top\cdot \hat{\mathbf{y}}) ~~~~~~~~\text{или}~~~~~~~~~~~~~~ \mathbf{W}= \mathbf{X}^{-1} \cdot \hat{\mathbf{y}}. $$В принципе, можно пользоваться любой из этих формул. Первая формула оказывается быстрее, если примеров N существенно больше чем признаков nX = число входов $\mathbf{x}$. Искать обратную матрицу для квадратной матрицы $\mathbf{X}^\top\cdot \mathbf{X}$ формы (nX+1, nX+1) проще, чем для матрицы $\mathbf{X}^{-1}$ формы (nX+1, N) во второй формуле, хотя при этом добавляется перемножение матриц $\mathbf{X}^\top\cdot \mathbf{X}$.
Пример на numpy
Проведём вычисление по полученным формулам при помощи библиотеки numpy. Краткое введение в numpy можно найти в документе NN_Base_Numpy.
Cгенерим сначала модельные данные в которых выходы линейно связаны с входами и добавлен небольшой случайный шум:
import numpy as np # работа с тензорами
N = 100 # число точек (примеров)
nX, nY = 2, 3 # число входов (признаков) и выходов
w = np.array([[ 1, 3, 5], # матрица w формы (nX,nY)
[ 6, 4, 2] ])
b = np.array( [ -3, -2, -1] ) # вектор b формы (nY, )
X = np.random.random ((N, nX)) # равномерные случ.точки в [0...1]
Y = np.dot(X, w) + b # выходы модели
Y += np.random.normal (0, 0.01, (N, nY)) # добавляем случайный гаусовый шум
Получим матрицы линейной модели по первой и второй формуле. Так как матрица во второй формуле не квадратная, для поиска обратной к ней матрицы используем функцию pinv, а не inv как в первом случае:
from numpy.linalg import inv, pinv # обратные для квадрат. и прямоуг. XX = np.concatenate( (X, np.ones((N, 1))), axis=1) # добавляем столбик единиц W1 = np.dot( inv(np.dot(XX.T, XX)), np.dot(XX.T, Y) ) # первая формула W2 = np.dot( pinv(XX), Y) # вторая формула
Регрессия на sklearn
Для решения этой-же задачи, на практике удобнее пользоваться готовой библиотекой машинного обучения Scikit-learn (кратко sklearn):
from sklearn.linear_model import LinearRegression
lr = LinearRegression().fit(X,Y)
print(lr.coef_.T) # [[1.007 3.001 5.001] матрица W
# [6.003 4. 1.998]]
print(lr.intercept_) # [-3.002 -2.001 -0.999] вектор b
Вызов LinearRegression() создаёт экземпляр класса данного метода обучения, которому через функцию fit передаются обучающие данные X,Y. Эта функция снова возвращает экземпляр класса, в атрибутах которого находятся параметры модели. Обратим внимание, что матрица $\mathbf{w}$ (атрибут lr.coef_) в sklearn хранится в транспонированном виде (по сравнению с принятым выше).
Получив параметры модели, можно теперь вычислить её mse-ошибку:
mse = np.mean((X @ lr.coef_.T + lr.intercept_ - Y) ** 2)
print(f"mse:{mse:.5f}, sqrt(mse):{np.sqrt(mse):.5f} ")
# mse:0.00010, sqrt(mse):0.01005
Классификация на sklearn
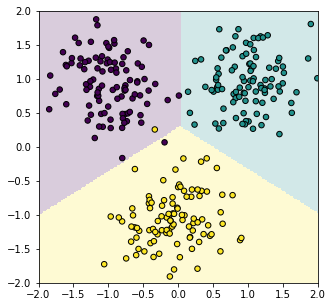
Задача классификации с нелинейными функциями сигмоида или софтмакса на выходе линейной модели не имеет такого простого решения. Поэтому приходится применять численные методы из которых в машинном и глубоком обучении оказался наиболее эффективным градиентный спуск. Тем не менее, в линейном случае можно успешно решить задачу многоклассовой классификации, отказавшись от нелинейности на выходе модели.
Рассмотрим для наглядности двумерное пространство признаков $\mathbf{x}=\{x_0, x_1\}$ и три класса $c=\{0,1,2\}$, к одному из которых необходимо отнести объект. У модели будет три выхода: $n_y=3$, на которых, в качестве целевых значений будем требовать для первого, второго и третьего классов соответственно: $$ \mathbf{y}=\{+1,-1,-1\},~~~~~\mathbf{y}=\{-1,+1,-1\},~~~~~\mathbf{y}=\{-1,-1,+1\}. $$ По-прежнему будем использовать среднеквадратичную ошибку, для которой есть точное решение. Естественно, линейная модель не сможет для всех примеров добиться целевых значений. Однако, три выхода модели $\mathbf{y}=\{d_0,d_1,d_2\}$ - это три знакопеременных расстояния от точки $\mathbf{x}$ до трёх плоскостей. Расстояния положительны, если вектор нормали "смотрит" на точку и отрицательны - если в противоположную сторону. Метод наименьших квадратов будет стремится развернуть эти векторы, чтобы, по крайней мере, совпадали знаки выхода модели и целевых значений. Это даст необходимый классификатор.
Подготовим модельные данные в виде трёх кластеров с нормальным разбросом точек вокруг их центров:
nx, ny, N = 2, 3, 300 # число признаков, классов, объектов (точек)
C = np.zeros(N) # номера правильных классов
Y = np.full((N,ny), -1) # матрица N x ny для выходов, заполненная -1
X = np.random.normal (0, 0.4, (N,nx)) # облако N точек с центром в начале координат
X0 = [[-1,1], [1,1], [0,-1]] # центры кластеров каждого класса
nc = int(N/ny) # число примеров каждого класса
for i, x0 in enumerate(X0):
C[i*nc:(i+1)*nc] = i # номер i-го класса
Y[i*nc:(i+1)*nc, i] = 1 # целевые выходы
X[i*nc:(i+1)*nc] += np.array(x0) # сдвигаем кластер i-го класса
Модель, которая проводит классификацию оформим в виде класса:
class Model:
def __init__(self):
"Конструктор"
self.lr = LinearRegression()
def __call__(self, x):
"Функциональный вызов объекта"
y = x @ self.lr.coef_.T + self.lr.intercept_
return np.argmax(y, axis=1)
def fit(self, x,y):
"Обучение по примерам x,y"
self.lr.fit(x,y)
Процесс обучения и тестирования выглядит следующим образом:
model = Model() # экземпляр модели model.fit(X,Y) # обучаем y = model(X) # поучаем номера классов A = (y==C).mean() # сравниваем с точными (аккуратность)
Чтобы получить график как в начале раздела, необходимо добавить к классу Model следующий метод:
. def plot(self, x1_min=0, x1_max=1, x2_min=0, x2_max=1, n=201):
# сетка точек 201 x 201 в интервале x1,x2=[xMin,xMax]
x1,x2 = np.meshgrid(np.linspace(x1_min, x1_max, n),
np.linspace(x2_min, x2_max, n))
grid = np.c_[x1.ravel(), x2.ravel()] # shape = (n*n, 2)
yp = self(grid).reshape(x1.shape) # (n*n, ) -> (n, n)
fig,ax = plt.subplots(figsize=(5, 5)) # размеры картинки (квадрат)
plt.axis([x1_min,x1_max, x2_min,x2_max]) # диапазон изменения осей
plt.imshow(yp, interpolation='nearest', # цвет. карту для 2D массива yp
extent=(x1.min(), x1.max(), x2.min(), x2.max()),
aspect='auto', origin='lower', alpha=0.2,
vmin=0, vmax=yp.max())
С помощью этого метода рисуем разделяющие поверхности и обучающие объекты:
model.plot(-2, 2, -2, 2) plt.scatter(X[:,0], X[:,1], c=C, s=30, edgecolors='black') plt.show()
