ML: Градиентный метод

Введение

В этом документе продолжается обсуждение многомерной линейной модели. На её примере мы рассмотрим метод стохастического градиентного спуска и выбор оптимальных гиперпараметров. Приведеный код на Python с использованием библиотек Numpy, PyTorch и Keras, можно найти в файле: ML_Line_Model.ipynb.

Градиентный метод

В сложных моделях точное аналитическое выражение для оптимальных параметров найти проблематично. Поэтому используют приближённые численные методы, основанные на том, что антиградиент функции локально направлен в сторону её уменьшения.

Обозначим набор параметров вектором $\mathbf{w}$. Ошибка является их функцией $L=L(\mathbf{w})$. В пространстве параметров существуют поверхности постоянного значения $L(\mathbf{w})=\mathrm{const}$. Смещение $d\mathbf{w}$ вдоль таких поверхностей не меняет $L$ и, следовательно, её диффернциал равен нулю:

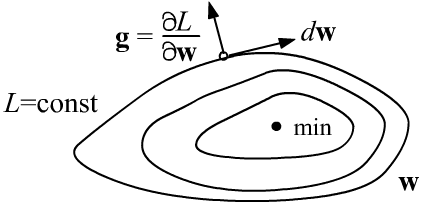
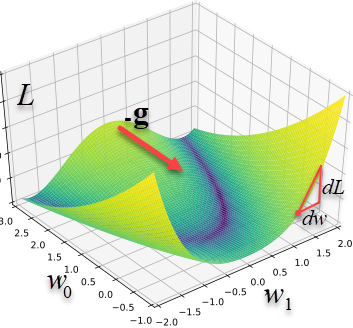$$ dL = \frac{\partial L}{\partial \mathbf{w}}\cdot d\mathbf{w} = \mathbf{g}\cdot d\mathbf{w} = 0, $$ $$ ~ $$ $$ \mathbf{g} = \frac{\partial L}{\partial \mathbf{w}} = \Bigr\{\frac{\partial L}{\partial w_1},..., \frac{\partial L}{\partial w_m} \Bigr\} $$

Такими образом, вектор градиента $\mathbf{g}$ перпендикулярен поверхностям $L=\mathrm{const}$ и направлен в сторону увеличения $L$ (как и любая производная). При приближении к минимуму длина градиента, обычно уменьшается, а в точке минимума (экстремум) она равна нулю (выше второй рисунок).

Чтобы найти минимум $L$, необходимо двигаться в обратном к градиенту направлении (вдоль антиградиента), с шагом пропорциональным некоторому числу $\lambda$.
Этот гиперпараметр называется скоростью обучения:

$$ \mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - \lambda\,\mathbf{g}^{(t)},~~~~~~~~~~~~~\mathbf{g}^{(t)} = \frac{\partial L}{\partial\mathbf{w}^{(t)}}. $$

Чем больше скорость обучения $\lambda$, тем быстрее параметры модели приближаются к оптимальным значениям. Однако при больших $\lambda$ существует риск проскочить минимум (несмотря на уменьшение длины градиента в его окрестности). Проиллюстрируем это примерами.

✍ В одномерном случае уравнение параболы с минимумом в точке $w=0$ и её "градиент" $g$ имеют вид: $$ L(w)=\frac{1}{2}\,\Gamma\,w^2,~~~~~~~~~~~~~g=\frac{dL}{dw}=\Gamma\,w, $$ где $\Gamma$ - константа. Спуск со скоростью $\lambda$ из точки $w^{(0)}$, на $t$-той итерации приводит в точку: $$w^{(t)}=(1-\lambda\,\Gamma)^t\,w^{(0)}.$$ При $\lambda > 1/\Gamma$ метод становится неустойчивым: $w^{(t)} \to \pm \infty$. Однако, чем ближе $\lambda$ снизу к критическому значению $\lambda_c = 1/\Gamma$, тем быстрее достигается минимум.

✍ Аналогично велёт себя градиентный спуск для "многомерной параболы" с различными коэффициентами $\Gamma_i$ по каждой координате: $$ L = \frac{1}{2}\sum_i \Gamma_i\,w_i ^2,~~~~~~~~~g_i = \Gamma_i\, w_i,~~~~~~w^{(t)}_i=(1-\lambda\Gamma_i)^t\,w^{(0)}_i. $$ Если мы находимся в точке $\mathbf{w}$, то кратчайший путь к минимуму $\mathbf{w}_{\text{min}}=\mathbf{0}$ будет в направлении вектора $-\mathbf{w}$. Однако градиентный метод будет изменять параметры в отличающемся направлении $-\mathbf{g}$ и поведёт к минимуму "окружным путём". Справа приведены траектории движения к минимуму $\{0,0\}$ в двумерном случае из различных начальных положений c $\Gamma=\{5, 1\}$ и $\lambda=0.1$. Обратим внимание не только на кривизну траекторий, но и на заметное уменьшение шага по мере приближения к минимуму. Критическое значение $\lambda_c$ определяется наибольшим коэффициентом параболы: $\lambda_c = 1/\max \Gamma_i = 0.2$.

Stochastic Gradient Descent

SGD (Stochastic Gradient Descent) - несколько более продвинутый градиентный метод оптимизации. В нём ошибка $L$ вычисляется не по всем данным, а по выборке (пачка, batch) размера batch_size. Это ускоряет сходимость, т.к. для вычисления очередного шага требуются не все данные, а лишь небольшое их подмножество. После каждой подправки параметров, выборка меняется (поэтому метод называется "stochastic"). При прохождении через все N примеров (одна эпоха), происходит int(N/btach_size) итераций (шагов в пространстве признаков).

Так как данных для вычисления $\mathbf{g}$ немного (обычно batch_size = 10-300), градиент от итерации к итерации может "вилять" в разные стороны. Чтобы уменьшить этот эффект, вектор $\mathbf{g}$ усредняется $\langle\mathbf{g}\rangle$ при помощи скользящего среднего. Это же усреднение помогает перемещаться по покрытой "мелкой рябью" поверхности. Степень сглаживания (усреднения) регулируется параметром $\beta=[0...1)$. Итерации $t=0,1,2,..$ метода SGD при $\langle\mathbf{g}\rangle_{(-1)}=0$ имеют вид:

$$ \mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - \lambda \,\langle\mathbf{g}\rangle^{(t)},~~~~~~~~~~~~ \langle\mathbf{g}\rangle^{(t)} = \beta\,\langle\mathbf{g}\rangle^{(t-1)} + (1-\beta)\,\mathbf{g}^{(t)}. $$

Величины batch_size и $\beta$ скоррелированы. Чем они больше, тем сильнее сглажен градиент. Увеличение batch_size замедляет обучение (за эпоху делается меньше итераций). Однако на графических карточках, благодаря быстрому перемножению больших матриц, увеличение batch_size может уменьшать время прохода по всем данным, даже в расчёте на одну итерацию.

☝ Скользящее среднее градиента имеет следующий смысл. С весами $\beta$ и $1-\beta$ (сумма которых равна 1) складываются среднее значение $\langle\mathbf{g}\rangle^{(t-1)}$ (полученное на предыдущей итерации) и текущий градиент $\mathbf{g}^{(t)}$. Чем ближе $\beta$ к 1, тем сильнее сглаживание $\langle\mathbf{g}\rangle^{(t)}\approx \langle\mathbf{g}\rangle^{(t-1)}$. При $\beta=0$ усреднения не происходит и $\langle\mathbf{g}\rangle^{(t)} = \mathbf{g}^{(t)}$.

Ниже приведен пример сглаживания данных при помощи скользящего среднего. Синяя линия - это одномерное стохастическое случайное блуждание (подобное цене на акцию). Гладкие жёлтая и зеленая линии - это усреднение с различным параметром $\beta$.

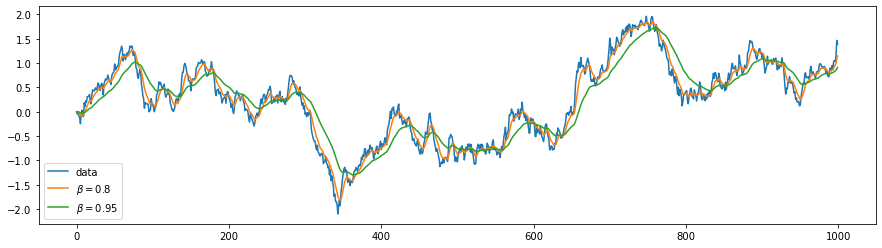
Понятно, что чем больше усреднение (ближе $\beta$ к единице), тем сильнее отстаёт среднее от исходных данных.

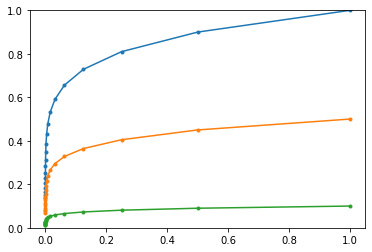
Если усредняемая величина равна константе $\mathbf{g}^{(t)}=\mathbf{g}=\text{const}$, то её среднее, через достаточно большое число итераций, также выйдет на эту константу (сумма геометрческой прогрессии): $\langle\mathbf{g}\rangle^{(1)} = \beta\,\mathbf{0} + (1-\beta)\,\mathbf{g}$, $$ \langle\mathbf{g}\rangle^{(2)} =\beta\,\langle\mathbf{g}\rangle^{(1)}+ (1-\beta)\,\mathbf{g}=(1+\beta)(1-\beta)\mathbf{g},....~~~~~~~~ \langle\mathbf{g}\rangle^{(t)} = (1+\beta+...+\beta^{t-1})(1-\beta)\,\mathbf{g} = (1-\beta^t)\,\mathbf{g}. $$

☝ В библиотеках PyTorch и Keras параметр $\beta$ называется momentum, а скорость обучения lr - это $\lambda\,(1-\beta)$ и $\langle\mathbf{g}\rangle^{(t)} \mapsto (1-\beta)\langle\mathbf{g}\rangle^{(t)}$. Кроме этого, метод SGD "includes support for momentum, learning rate decay, and Nesterov momentum". Распад означает уменьшение lr с каждой эпохой iterations в соответствии с параметром распада decay (код из Keras): 

lr_t = lr * (1. / (1. + decay * iterations ))
Далее происходят вычисления: 
v = momentum * v - lr_t * grad
if nesterov:  params = params + momentum * v - lr_t * grad
       else:  params = params + v

По умолчанию приняты следующие параметры: SGD(lr=0.01, momentum=0.0, decay=0.0, nesterov=False).

Вычисление градиента

Найдём градиент от среднеквадратичной ошибки (MSE) в линейной модели. Для этого воспользуемся правилом дифференцирования сложной функции. В данном случае $L$ зависит от $y_{i\gamma}$, которые уже непосредственно зависят от параметров: $y_{i\gamma}=\sum_\mu\,x_{i\mu}w_{\mu\gamma}+b_{\gamma}$. Поэтому для среднеквадратичной ошибки $L= \langle (\mathbf{y}-\hat{\mathbf{y}})^2\rangle$, усреднённой по $N$ примерам (первый индекс) и $m$ выходам модели (второй индекс) имеем:

$$ \frac{\partial L}{\partial w_{\alpha\beta}} = \sum_{i, \gamma} \frac{\partial L}{\partial y_{i\gamma}} \, \frac{\partial y_{i\gamma}}{\partial w_{\alpha\beta}} = \frac{2}{N\,m} \sum_{i, \gamma} (y_{i\gamma}-\hat{y}_{i\gamma})\,\sum_\mu\,x_{i\mu}\,\delta_{\mu\alpha}\,\delta_{\gamma\beta} = \frac{2}{N\,m} \sum_{i} x_{i\alpha}\, (y_{i\beta}-\hat{y}_{i\beta}). $$

Аналогично для градиента по $\mathbf{b}$:

$$ \frac{\partial L}{\partial b_{\alpha}} = \frac{2}{N\,m} \sum_{i} (y_{i\alpha}-\hat{y}_{i\alpha}). $$

В матричном виде это можно записать так:

$$ \frac{\partial L}{\partial \mathbf{w} } = \frac{2}{N\,m}~\mathbf{x}^\top\cdot(\mathbf{y}-\hat{\mathbf{y}}),~~~~~~~~~~~~~ \frac{\partial L}{\partial \mathbf{b} } = \frac{2}{N\,m}~\mathrm{sum}(\mathbf{y}-\hat{\mathbf{y}},~ \mathrm{axis}=0). $$

Произведение $N\,m$ равно числу элементов массива $\mathbf{y}$, которые в numpy находятся в атрибуте size.

Численный поиск минимума

Приведём алгоритм поиска оптимальных параметров методом SGD при помощи библиотеки numpy. Ошибку будем вычислять по batch_size примерам, проходя по всем обучающим примерам epochs раз: 

def Loss(X,Y, W, B):                                     # функция ошибки
    return np.mean((X @ W + B - Y) ** 2)

def My_SGD(X, Y, lr, mo, batch_size, epochs):
    
    W = np.random.random ((nX, nY))                      # случайные начальные значения
    B = np.random.random ((nY, )  )                      # параметров модели W,B

    agW, agB, iters = 0, 0, int( len(X)/batch_size )     # средние градиенты, число батчей
        
    for epoch in range(epochs):                          # эпоха - проход по всем примерам
        idx = np.random.permutation( len(X) )            # перемешанный список индексов
        X, Y = X[idx], Y[idx]                            # перемешиваем данные 
        
        for i in range(0, iters*batch_size, batch_size): # примеры разбиты на пачки 
            xb = X[i: i+batch_size]                      # входы пачки
            yb = Y[i: i+batch_size]                      # выходы пачки (целевые значения)
        
            y = xb @ W + B                               # выходы модели
        
            gW = (2 / y.size) * xb.T @ (y - yb)          # градиент по w
            gB = (2 / y.size) * np.sum(y - yb, axis=0)   # градиент по b
        
            agW = mo*agW + (1-mo)*gW;   W -= lr * agW    # сглаживаем градиенты и
            agB = mo*agB + (1-mo)*gB;   B -= lr * agB    # подправляем параметры
        
    return W, B, Loss(X,Y, W, B)                         # параметры и ошибка

Обратим внимание, что обучающие примеры перед началом каждой эпохи случайно перемешиваются. Для этого, при помощи функции np.random.permutation создаётся перемешенный список целых чисел о 0 до len(X)-1. Следующая строчка собственно производит перемешивание. Перемешивать данные перед каждой эпохой в принципе не обязательно, но если данных немного это может улучшить сходимость к минимуму. Кроме этого, если число примеров N нацело не делятся на batch_size, не все данные попадут в вычисление градиента. Перемешивание ослабляет эту проблему.

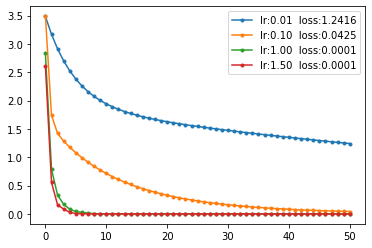
Справа приведены графики ошибки при различных скоростях обучения и mo=0. Критическое значение lr находится в районе 1.75. При приближении к этому значению скорость обучения заметно возрастает.

Оптимальные гиперпараметры

Любой метод оптимизации зависит от гиперпараметров, выбор которых иногда оказывается очень важным.

Нарисуем карту высот ошибки Loss линейной модели, как функцию гиперпараметров $\lambda$ (=lr) и $\beta$ (=mo).
Синий цвет - минимум ошибки, коричневый - максимум. Количество эпох epochs = 10 и размер пачки batch_size = 10 фиксированы (точек N=100). Голубая линия с точками означает значение $\beta$ соответствующее минимальной ошибке при данном $\lambda$. Под картой высот приведен график ошибки как функции $\lambda$ (при оптимальном $\beta$ для данного $\lambda$). Коричневый цвет на карте высот соответствует области неустойчивости градиентного метода:

Как видно, для такой простой модели, при $\beta \sim 0.8$, значение $\lambda$ может меняться в широких пределах. Оптимальные гиперпараметры: mo=0.63, lr=5.31, loss=0.00013. Отметим, что подходящая параметризация гиперпараметров важна.
Например, если выбрать как в Keras lr=$\lambda\,(1-\beta)$, то получится менее устойчивая картина:

Оптимальные гиперпараметры в этом случае: mo=0.58, lr=2.25, loss=0.00013.

Градиент на графе в PyTorch

Библиотека PyTorch от Facebook является популярным инструментом при разработки сложных архитектур нейронных сетей. PyTorch создаёт динамический вычислительный граф (строится в процессе вычислений и не требует компиляции).

Воспроизведём на PyTorch простой градиентный метод. Параметры модели W,B являются терминальными узлами вычислительного графа, для которых будет вычисляться градиент (requires_grad=True):

Метод randn возвращает тензор нормально распределённых случайных чисел. По умолчанию они имеют тип float32. Чтобы он совпадал с типом обучающих данных X,Y, происходит явное задание типа аргументом dtype.

Затем идёт основной цикл вычислений: 

import torch

def grad_tourch(X, Y, lr=1, batch_size=10, epochs=10):
    W = torch.randn(nX, nY, dtype=torch.float64,  requires_grad=True)
    B = torch.randn(nY,     dtype=torch.float64,  requires_grad=True)

    for epoch in range(epochs):                          # эпоха - проход по всем примерам
        
        idx = torch.randperm( len(X) )                   # перемешанный список индексов
        X, Y = X[idx], Y[idx]                            # мешаем данные
        
        sumL, iters = 0, int( len(X)/batch_size)         # суммарная ошибка и число батчей 
        
        for i in range(0, iters*batch_size, batch_size): # примеры разбиты на пачки 
         
            xb = torch.from_numpy(X[i: i+batch_size])
            yb = torch.from_numpy(Y[i: i+batch_size])
            
            y = xb.mm(W).add(B)                          # модель y = bx @ W + B
            loss = ((y-yb)**2).mean()                    # mse ошибка по батчу
            sumL += loss.data.item()

            loss.backward()                              # вычисление градиентов
                                                
            with torch.no_grad():   
                W.add_(- lr *  W.grad)                   # без перестраивания графа
                B.add_(- lr *  B.grad)            
            
            W.grad.zero_()                               # обнуляем градиенты
            B.grad.zero_()                               
            
        print(f"{epoch:3d}({iters})  loss:{sumL/iters:0.5f}")

    return W, B

grad_tourch(X, Y)

Вначале формируются torch-тензоры пачек из numpy-тензоров (новая память при этом не выделяется). Затем строится вычислительный граф, корнем которого будет ошибка модели loss. Попутно происходят вычисления на графе. Затем для корня запускается метод backward, который возвращается по веткам и вычисляет градиенты.

Любое выражение с тензорами, имеющими свойство requires_grad=True приводит к динамической перестройке вычислительного графа, ведущего к его корню (ошибке модели loss). Чтобы этого не произошло, после backward устанавливается окружение no_grad(), которое блокирует изменение графа При этом, меняя параметры, мы не создаём новых тензоров (функция add_ это "инкрементация"). После изменения W,B необходимо сбросить в ноль градиенты (для следующей итерации).

Нейронная сеть на PyTorch

Параметры линейной модели можно также найти при помощи нейронной сети из одного слоя без активационной функции: 

import torch.nn as nn

model = nn.Sequential( nn.Linear(nX, nY) )

Создадим SGD оптимизатор (который будет подправлять параметры) и mse функцию ошибки: 

optimizer = torch.optim.SGD(model.parameters(), lr=1, momentum=0.9)
criterion = nn.MSELoss()

Цикл обучения выглядит следующим образом. На каждой итерации на сеть передают пачку примеров y=model(xb), в результате чего происходит прямое распространение (forward). Полученный выход сети y, вместе с "истинными" значениями yb передают функции ошибки. Для неё вызывают обратное распространение backward, в результате которого будут вычислены градиенты. Метод оптимизатора step, при помощи этих градиентов, подправляет параметры модели. Затем оптимизатор обнуляет градиенты (zero_grad): 

iters = int( len(X)/batch_size )
for epoch in range(epochs):                           # эпоха - проход по всем примерам
    for i in range(0, iters*batch_size, batch_size):  # примеры разбиты на пачки 
        bx = torch.Tensor( X[i: i+batch_size] )       # по numpy массивам создаём
        by = torch.Tensor( Y[i: i+batch_size] )       # тензоры torch типа float32
    
        y = model(bx)                                 # прямое распространение
        
        loss = criterion(y, by)                       # вычисляем ошибку
        loss.backward()                               # вычисляем градиенты
         
        optimizer.step()                              # подправляем параметры
        optimizer.zero_grad()                         # обнуляем градиенты
            
    print('epoch: %d  Loss: %.6f'  % (epoch,  loss) )

После обучения можно вывести параметры модели: 

print(model[0].weight, model[0].bias)
Матрица весов weight, как и в sklearn, хранится в транспонированном виде.

Нейронная сеть на Keras

Библиотека Keras является простым в использовании инструментом для проектирования нейронных сетей. В настоящее время она является составной частью фреймворка tensorflow от Google.
Введение в Keras можно найти в документе NN_Base_Keras.

Линейная модель (один слой без активационной функции) в Keras реализован в полносвязном слое Dense. Создания нейронной сети с одним таким слоем делается следующим образом: 

from   tensorflow       import keras              # keras из tensorflow
from   keras.models     import Sequential         # способ формирования слоёв (стопка)
from   keras.layers     import Dense              # полносвязный слой
from   keras.optimizers import SGD                # метод оптимизации

model = Sequential()                              # линейная стопка слоёв
model.add(Dense(units=nY, input_dim=nX))

После создания модели, она компилируется (compile) и запускается её обучением (fit). При обучении будем использовать SGD-оптимизатор и mse-ошибку: 

model.compile(optimizer = SGD(lr=2, momentum=0.5), loss = 'mse') 

res = model.fit(X, Y, batch_size=batch_size, epochs=10,  verbose=0 ) )
После обучения можно вывести график ошибок, как функцию числа эпох: 
plt.plot(res.history['loss'], marker=".")
plt.legend(["loss: %.5f"  % ( res.history['loss'][-1] )])
plt.show()
Параметры каждого слоя (в нашем случае слой один) находятся в списке, получаемом методом слоя get_weights(). Поэтому веса и смещения линейной модели (или в общем случае многослойной полносвязной модели) выводятся следующим образом: 
for lr in model.layers:                           # по всем слоям
    w = lr.get_weights()[0]                       # веса синапсов нейронов
    b = lr.get_weights()[1]                       # смещения нейронов
    ...