ML: Введение в PyTorch: 1. Тензоры

Введение

Библиотека PyTorch является универсальным инструментом машинного обучения. Она популярна при проектировании новых архитектур нейронных сетей. Является open-source проектом и поддерживается компанией Facebook. В библиотеке есть четыре ключевых составляющих:

PyTorch необходимо установить, выбрав правильную конфигурацию на странице проекта и подключить библиотеку: 

import torch

e  = torch.eye(2)                    # единичная матрица 2x2
print(e)                             # tensor([[1., 0.],
                                               [0., 1.]])

Для чтения этого документы желательно уверенное владение библиотекой numpy, в частности такими понятиями как размерность тензора, его форма и то, как они изменяются при различных операциях. Ниже мы рассмотрим основы работы с тензорами. Следующие документы посвящены вычислительным графам и нейронным сетям в PyTorch.

Создание тензоров

Тензоры с вещественными компонентами типа float32 создаются следующим образом: 

v = torch.empty(10)                      # вектор из 10 элементов float32 (мусор)
m = torch.empty(2, 3)                    # матрица формы (2,3)    float32 (мусор)
x = torch.empty_like(m)                  # с мусором, такой же формы как m
Тензор можно также создать по списку Python или массиву numpy: 
x = torch.tensor( [ [0,1,2], [3,4,6] ] ) # матрица формы  (2,3) int64 из списка
s = torch.tensor(137.)                   # скаляр (dim=0) типа  float32 (точка!)
s = torch.tensor(137, dtype=torch.double)# тоже, но типа float64 (хотя и без точки)
                                 
e = torch.from_numpy( np.eye(3) )        # из numpy-тензора (с его памятью)

print( x )                               # tensor([[0., 1., 2.], [3., 4., 6.]])
print( x.numpy() )                       # numpy-тензор (в той же памяти)
Основные свойства тензора - это его размерность (число индексов), форма (размерности индексов), тип элементов и их количество: 
print( x.dim(),  x.type(), x.numel() )   # размерность, тип элементов, их количество
print( x.size(), x.shape )               # torch.Size([2, 3]) форма (эквивалентны)
print( tuple(x.shape), *x.shape )        # (2, 3) 2 3 форма 

print( s.item(), s.dim()  )              # 137 0 (для скаляра или матрицы с одним эл.)

Тензор можно создавать при помощи конструкторов. Доступны следующие типы (вместо torch.FloatTensor(...) можно писать torch.Tensor(...)): 

   HalfTensor   - float16,      ShortTensor - int16,        CharTensor - int8,       
   FloatTensor  - float32,      IntTensor   - int32,        ByteTensor - uint8,
   DoubleTensor - float64,      LongTensor  - int64,        BoolTensor - bool.
При преобразовании типа (если он меняется) под данные выделяется новая память: 
x = torch.Tensor(2,3)                    # матрица (2,3) из 6 элементов float32 (мусор)
y = x.long()                             # int64   новый тензор 
y = x.float()                            # float32 новый тензор
y = x.double()                           # float64 новый тензор
Тип элементов можно также указывать в методе empty или функциях инициализации (см ниже): 
x = torch.empty(2,3, dtype=torch.float64)# матрица 2x3 с мусором float64
x = torch.empty(2,3, dtype=torch.double) # тоже самое
y = torch.zeros(2,3, dtype=torch.int64)  # матрица 2x3 нулей     int64
y = torch.zeros(2,3, dtype=torch.long)   # тоже самое

y.element_size()                         # 8 - размер в байтах элемента

Инициализация значений

При создании тензор можно сразу инициализировать значениям (по умолчанию типа float == float32): 

y = torch.zeros (2, 3)                   # матрица 2x3 из нулей  типа float32
x = torch.zeros_like(y)                  # такой же формы как y из нулей

x = torch.ones (2, 3)                    # матрица 2x3 из единиц 
x = torch.ones_like(y)                   # такой же формы как y из единиц

x = torch.full((2, 3), 3.14159265)       # заполнить матрицу 2x3 числом pi 

x = torch.eye   (3)                      # единичная матрица 3x3
x = torch.eye   (2,3)                    # "единичная" не квадратная [[1., 0., 0.], 
                                         #                            [0., 1., 0.]]
x = torch.linspace(0,2,5)                # [0.0,0.5,1.0,1.5,2.0] [beg,end], num

x = torch.rand (2, 3)                    # 2x3 равномерно случ.матрица [0...1]
x = torch.randn(2, 3)                    # 2x3 нормально  случ.матрица (mean=0, var=1)

x = torch.empty(3).uniform_(0, 1)        # вектор с равномерным распределением [0..1]
x = torch.empty(3).normal_(mean=0,std=1) # вектор с нормальным распределением
Следующие методы по умолчанию возвращают элементы типа long == int64: 
x = torch.arange(4)                      # [0,1,2,3]             [0,end)
x = torch.arange(2,14,3)                 # [2,5,8,11]            [beg,end), step

x = torch.randperm(10)                   # [8,6,9,3,5,0,1,4,7,2] - случ.перестановка
x = torch.randint (1, 10, (2,3))         # 2x3 случ.целых из интервала [1...10)

Управление памятью

У многих методов есть вторая версия, имя которой оканчивается подчёркиванием (in-place функции). Например, экспонента от элементов тензора: x.exp() или torch.exp(x) возвращает новый тензор. Метод x.exp_() вычисляет экспоненту от элементов x и записывает значения на место этих же элементов, т.е. новая память не выделяется (метод item() возвращает единственный элемент тензор как число): 

x = torch.ones(1)                        # вектор из одной компоненты
y = x.exp()                              # разная память:
print(x); y[0]=2;  print(x.item())       # tensor([1.])      1.0

y = x.exp_()                             # одна память:
print(x);  y[0]=2;  print(x.item())      # tensor([2.7183])  2.0
Эту же семантику использует метод fill_, который присваивает всем элементам данное значение или метод обнуления всех элементов zero_: 
x = torch.empty(2, 3).fill_(-1)          # матрица из -1
x.zero_()                                # теперь нули (в том же тензор)

Оператор присваивания, как обычно, происходит по ссылке (данные расшариваются). Если нужна копия данных, её можно получить методом clone или copy_: 
y = x                                    # y и z - один объект
y = x.clone()                            # копирование 

y.copy_(x)                               # копирует в себя x (broadcastable)
y = torch.empty_like(x).copy_(x)         # выделяем память и копируем

Для "обычных" тензоров copy_ и clone приводят к одинаковому результату. Разница начинается при построении графа вычислений (см. ниже).

Операции

Большинство операций с тензорами такие же как и в библиотеке numpy: 

x1, x2 = torch.ones(2,3),  torch.ones(2,3)  

x1[0]   = 2           # меням первую строчку на 2 [ [2., 2., 2.],  [1., 1., 1.]]
x2[:,1] = 3           # меням вторую колонку на 3 [ [1., 3., 1.],  [1., 3., 1.]]

y = x1 + x2           # складываем                [ [3., 5., 3.],  [2., 4., 2.]]

Сложение, вычитание, умножение и деление (без свёртки) можно делать инкрементным (в той-же памяти): 

x += y
x.add_(y)             # к тензору x добавили y (инкриментация)
x.add_(y, alpha=2.0)  # x += 2*y (так быстрее для больших тензоров)

x *= y
x.mul_(y)

При помощи тензора индексов можно делать выборки элементов: 

a = torch.ByteTensor(2,3).random_() # случайные байты [[185,  16, 242], [223, 147, 202]]

print(a > 128)                      # [[ True, False,  True], [ True,  True,  True]]
a[a > 128]                          # [185, 242, 223, 147, 202] - элементы, большие 128

Полезным примером таких операций является синхронное перемешивание тензоров (создаётся новая память): 

X = torch.arange(10)                # [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Y = -X                              # [ 0,-1,-2,-3,-4,-5,-6,-7,-8,-9]

idx = torch.randperm(X.shape[0])    # перестановка индексов
X = X[idx]                          # [ 4, 9, 7, 3, 2, 0, 5, 6, 1, 8]
Y = Y[idx]                          # [-4,-9,-7,-3,-2, 0,-5,-6,-1,-8]

Конкатенацию тензоров можно делать вдоль определённой оси или стопками: 

x1 = torch.arange(-3,0)             # [-3, -2, -1]
x2 = torch.arange(3)                # [ 0,  1,  2]

torch.cat([x1, x2], dim=0)          #  [-3, -2, -1,  0,  1,  2]    конкатенация 
torch.stack([x1, x2])               # [[-3, -2, -1], [ 0,  1,  2]]

Тензорные свёртки

Все функции этого раздела есть в двух эквивалентных версиях: x.mm(y) и torch.mm(x,y). 

v.dot(u)                # cкалярное умножение - только 1D векторов
x.mv(v)                 # матрица на вектор: (n,s) (s)   = (n)
x.mm(y)                 # только 2D матриц : (n,s) (s,m) = (n,m)

x.bmm(y)                # для 3D тензоров:   (b, n,s) (b, s,m) =   (b, n,m)
x.matmul(y)             # аналог из numpy: (j,1, n,s) (k, s,m) = (j,k, n,m)

torch.addmv(t, m, v, beta=1, alpha=1)  #  alpha*(m  @ v)  + beta*t
torch.addmm(t,m1,m2, beta=1, alpha=1)  #  alpha*(m1 @ m2) + beta*t

Много функций выполняют вычисления либо со всеми элементами, либо по одному из индексов (вдоль оси). Ниже это ось 1 (второй индекс): 

x = torch.Tensor([[2,1,3],
                  [1,2,1]])
x.sum(1)                # [6., 4.]   cумма     
x.mean(1)               # [2., 1.33] cреднее   
x.prod(1)               # [6., 2.]   произведение 

x.argmin(1)             # [1, 2]

v,i = x.topk(2, dim=1)  # 2 наибольших значений и их индексов
Аналогично: std(), var(), median(), max(), min().

Изменение формы

Форма тензора (число индексов и их размерности) меняется функциями view и reshape: 

torch.arange(6).view(2,3)         #    tensor([[0, 1, 2],
torch.arange(6).reshape(2,3)      #            [3, 4, 5]])
В этих функциях перечисляются новые размерности индексов (их произведение должно совпадать с числом элементов). Одна из размерностей может быть равна -1 и тогда она будет посчитана автоматически. Например, выше можно было бы написать view(-1,3) или view(2,-1). Можно также изменять форму, используя другой тензор с тем-же числом элементов: 
a, b = torch.zeros(2,5), torch.zeros(10)
b.view_as(a)

Напомним, что тензоры принято изображать в табличной форме: вектор (ndim=1) - это строка чисел, матрица формы (rows,cols) - это прямоугольная таблица с rows строчками и cols колонками. Трёхмерный тензор (три индекса, ndim=3) изображают в виде стопки матриц:

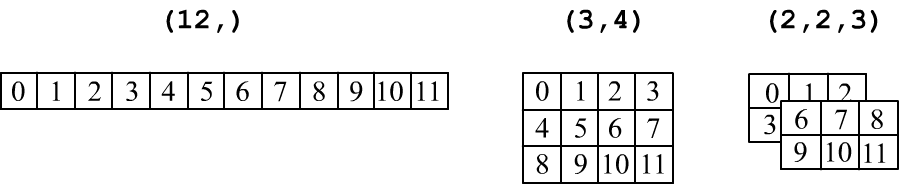
Операция транспонирования (перестановка местами столбцов и строк): t() или t_() разрешена только для 2D матриц: 

z = x.t()                              # сам x не меняется
z = x.t_()                             # меняется x
Перестановка любых двух осей (индексов) в тензорах произвольной размерности делается методом transpose: 
x.transpose(1, 2)                      # перестановка осей 1 и 2
Напомним, что x.t() не тоже самое, что x.view(x.shape[1], x.shape[0]).

Ещё более универсальный способ перестановки индексов: 

x = torch.randn(3, 5)               
x.permute(1, 0) == x.t()               # эквивалентно транспонированию

x = torch.randn(2, 3, 5)
x.permute(2, 0, 1).size()              # torch.Size([5, 2, 3])

Элементы в памяти

Форма тензора (x.size() или x.shape) - это способ нумерации линейно упорядоченных элементов тензора при помощи x.dim() индексов. Метод x.stride() даёт набор смещений на которые умножаются индексы, для получения соответствующего элемента (от указателя на начальный): 

x[i,j,k] = x + stride[0]*i  #  shape[1]*shape[0]
             + stride[1]*j  #  shape[0]
             + stride[2]*k  #  1                          (псевдокод)
Например: 
x = torch.arange(935).view(5,17,11)    #     11*17
print( x.stride(), x[1,1,1].item() )   #< (187, 11, 1) 199=187+11+1
При изменении формы view меняется x.stride(), но не данные в памяти. Однако, при этом может возникнуть ситуация, когда строки матрицы будут в памяти идти не последовательно друг за другом. Ниже на рисунке тензор x это 2D матрица формы (2,3). Её элементы в памяти идут последовательно и построчно. Операция транспонирования (без подчёркивания) исходный тензор не меняет и возвращает ссылку на те же данные, но с другим stride. В результате её строки в памяти "перепутываются". Если вызвать метод y.contiguous(), то будет создана новая память, куда перенесутся элементы, так, чтобы строки шли последовательно:

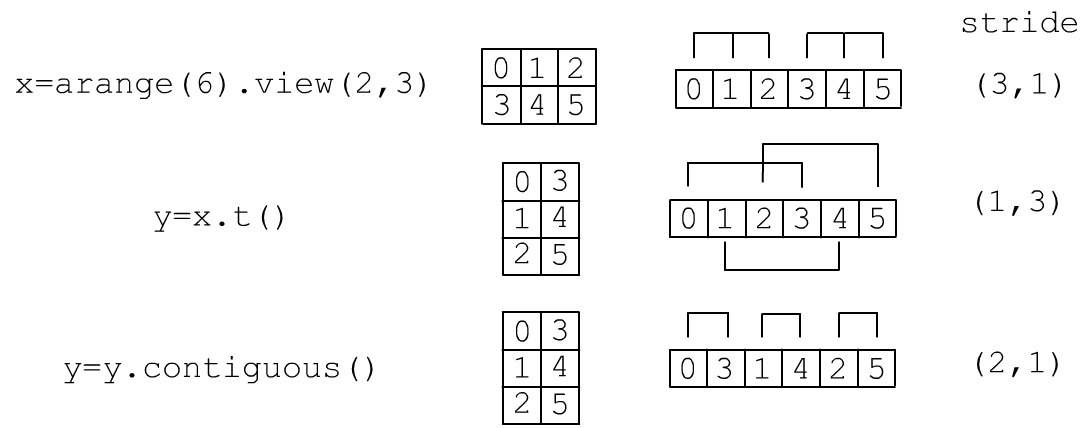
Проверить находятся ли строки тензора в памяти последовательно можно так: 

print( x.is_contiguous() )             # True - непрерывно построчно
Для произвольной размерности этот метод проверяет условие stride[i]=stride[i+1]*size[i+1] для всех индексов. Если это не так, методом x = x.contiguous() можно перенести данные в непрерывный фрагмент.

Изменение формы методом reshape сначала проверяет is_contiguous и если она False вызывает contiguous (создаёт новую память). После этого вызывается view. Так, в примере на картинках для операции y=x.t() тензоры x,y имеют общие данные (по ссылке), а после y = y.contiguous() уже нет.

Таким образом, reshape может вернуть данные как по ссылки, так и по значению. Метод view возвращает всегда по значению, но может выдать ошибку, если нарушается условие is_contiguous.

Вычисления на GPU

Перемножим две большие единичные матрицы. На центральном процессоре Intel i3-3220 3.3GHz, 16Gb это займёт 35 секунд: 
x1 = torch.eye(10000)
y1 = torch.eye(10000)
z1 = x1.mm(y1)                         # 35s
Если на компьютере есть графическая карта (например, NVIDIA GeForce GTX 1050 Ti), то можно создать дополнительное вычислительное устройство (ноль означает номер графической карты): 
torch.cuda.device_count()              # число доступных GPU

cpu = torch.device("cpu")
gpu = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
Повторим эти же вычисления, создавая и перемножая тензоры непосредственно в GPU: 
x1 = torch.eye(10000, device = gpu)
y1 = torch.eye(10000, device = gpu)
z1 = x1.mm(y1)                         # 0.04s
На самом деле, чаще тензоры создаются в памяти CPU, затем методом to пересылаются в GPU, там перемножаются и возвращаются обратно в CPU: 
x1 = torch.eye(10000).to(gpu)
y1 = torch.eye(10000).to(gpu)
z1 = x1.mm(y1).to(cpu)                 # 2s

Размер занятой памяти GPU можно получить следующим образом: 

from GPUtil import showUtilization as gpu_usage
gpu_usage()
Иногда её необходимо очищать "руками:" 
torch.cuda.empty_cache()
Полезные статьи по вычислениям на GPU: