ML: Введение в PyTorch: 2. Графы

Введение
Прямой и обратный проходы
Построение графа
Вычисление градиентов
Градиент в промежуточных узлах
Приостановка построения графа

Отсоединение узла от графа
Немного примеров
Что нельзя делать с листьями графа
Срезы теноров
Визуализация
Минимизация функции

Введение

В этом документе содержится продолжение описания работы с тензорами в PyTorch. Теперь мы рассмотрим вычислительные графы и распространение на них градиентов. Следующий документ посвящен основам работы с нейронными сетями.

Прямой и обратный проходы

Напомним, что вычислительный граф является последовательностью действий для получения значения некоторой величины. В машинном обучении обычно это скалярная функция ошибки (тензор нулевой размерности). Результат вычисления получается при прямом проходе по графу. Ниже нарисован граф для функции $z = x\cdot x + \sin(2\cdot y)$ и приведены значения узлов (зелёный цвет) при x=4 и y=3.14159265:

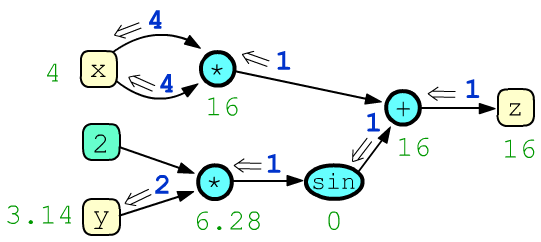
$$ z = x\cdot x + \sin(2\cdot y) $$ $$ \begin{array}{lcl} g_x = \frac{\displaystyle\partial z}{\displaystyle\partial x} &=& 2\cdot x\Bigr|_{x=4} = 8,\\[4mm] g_y = \frac{\displaystyle\partial z}{\displaystyle\partial y} &=& 2\,\cos(2\cdot y)\Bigr|_{y=\pi} = 2. \end{array} $$

После прямого прохода по графу (от листьев к корню $z$ дерева), запускается процедура обратного прохода, вычисляющая производные (градиенты, синий цвет) целевого выражения $z$ по остальным узлам графа. На рисунке из узла z выходит $g_z=1$. Суммарный $g_x=8$, входящий в узел x, равен частной производной $\partial z/\partial x$, a $g_y=2$, входящий в y, равен $\partial z/\partial y$. С деталями вычисления градиентов стоит ознакомиться в документе "Вычислительный граф".

В PyTorch графы динамические. Они строятся по ходу вычисления выражений. Чтобы повторить вычисления с новыми данными, необходимо повторно "пройти" по всем выражениям. Этот подход отличен от статических графов, которые строятся в tensorflow. Статический граф определяется один раз, компилируется и потом может произвольное число раз запускаться на вычисления с различными значениями в листовых узлах, но при этом не может быть изменён.

Построение графа

Тензор в PyTorch, по-мимо данных со значениями элементов, может хранить градиенты по этим элементам и многое другое, необходимое для работы с вычислительным графом:

from torch import tensor, empty, ones, zeros

v  = zeros(2)                # 2D - вектор из нулей

print(v.data)                # tensor([0.,0.])  - данные тензора (тоже, что просто v)
print(v.grad)                # None             - градиент по тензору (пока его нет)
print(v.grad_fn)             # None             - функция к нему привела (пока нет графа)
print(v.is_leaf)             # True             - является листом графа (да)
print(v.requires_grad)       # False            - по нему нужен градиент (пока не нужен)

Все операции с тензором v выполняются с его атрибутом v.data. Атрибут v.grad (если он есть) является тензором той-же размерности, что и v (у него также есть data, grad,..., и т.д.).

В PyTorch граф начинает строиться, если в выражении есть тензор с атрибутом requires_grad в значении True.
Этот атрибут можно задать в конструкторе (при создании тензора) или в любой момент позже:

x = ones(2, requires_grad=True)          # вектор [1., 1.] сразу будет узлом графа

y = empty(2).fill_(3)                    # сначала создали вектор [3.,3.],
y.requires_grad = True                   # а позже объявили его узлом

print(y)                                 # tensor([3., 3.], requires_grad=True)

Атрибут requires_grad "заразный" и если в выражении есть хотя бы один такой тензор, возникает граф. Каждый его не листовой узел содержит последнюю операцию которая к нему приводит (в атрибуте grad_fn):

z = (y*y).sum()                          # скаляр (dim=0) y[0]**2 + y[1]**2
 
print(z)                                 # tensor(18., grad_fn=<SumBackward0>)
print(y.is_leaf, z.is_leaf)              # True False
print(y.requires_grad, y.grad_fn)        # True None
print(z.requires_grad, z.grad_fn)        # True <SumBackward0>

Узел y является листом (is_leaf), тогда как z - нет (он является корневым = финальным узлом дерева).

Вычисление градиентов

Метод backward() корневого узла графа запускает процедуру вычисления градиентов в листовых (is_leaf) узлах, имеющих атрибут requires_grad.
Для примера выше число 1, проходя через узел суммы, дублируется столько раз, сколько было суммирований, превращаясь в вектор [1,1]. Затем на узле произведения без свёртки он умножается на противоположный аргумент:

print(y.grad)                              # None
z.backward()                               # запускаем вычисление градиентов
print(y.grad)                              # tensor([6., 6.]) - сумма 2-х входящих grad

Повторно метод backward() вызвать нельзя (только снова перестроив граф). Исключение составляет такой его вызов: z.backward(retain_graph = True). Но в этом случае градиенты будут накапливаться (суммироваться).

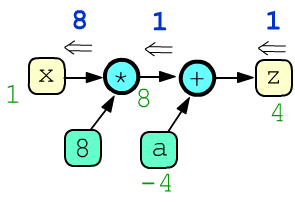Листовые узлы без атрибута requires_grad=True считаются константами и по ним градиент не вычисляется. Ниже есть две константы (8, a) :

x = ones(1, requires_grad=True)
a = tensor(-4.)
z = 8*x + a

z.backward()

print(x, x.grad)         # tensor([1.], requires_grad=True), tensor([8.])
print(a, a.grad)         # tensor([-4.]), None
print(z)                 # tensor([4.], grad_fn=<AddBackward0>)

При анализе вычислительного графа, стоит помнить, что любая переменная (листовая или промежуточная) всегда представляется одним узлом. Если переменная используется в различных вычислениях, то из неё выходит несколько ребер, по которым затем (при обратном распространении) входят (суммируясь) несколько градиентов. Таковым являлся узел y в примере из начала раздела.

Градиент в промежуточных узлах

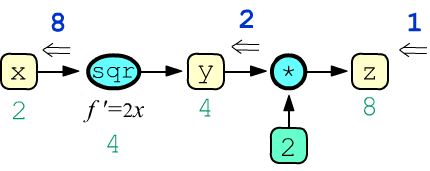По умолчанию промежуточные (не листовые) узлы графа не хранят прошедшие через них градиентов. Эту ситуацию можно изменить,
вызвав для для конкретного узла метод retain_grad:

x = tensor(2., requires_grad=True)

y  = x**2;    y.retain_grad()                    
z  = 2*y;     z.retain_grad()       

z.backward()

print(z.item(),     y.item(),     x.item())      # 8.0 4.0 2.0
print(z.grad.item(),y.grad.item(),x.grad.item()) # 1.0 2.0 8.0

В этом примере корнем дерева вычислений является тензор z, а единственным листом, требующим градиента по умолчанию - узел x. Узел y - это промежуточный узел.

Приостановка построения графа

Граф должен строится каждый раз при повторном вычислении градиентов:

for i in range(1,3):
    x = empty(2).fill_(i).requires_grad_(True)
    
    z = x.dot(x)                           # граф
    z.backward()                           # получаем градиенты
    
    print(z.item(), x.grad)

Выше в цикле два раза создаётся новый тензор x, затем вычислительный граф для получения суммы квадратов его компонент: $z=x^2_0+x^2_1$. Градиент от листовой переменной равен: $\partial z/\partial x_i = 2x_i$.

Иногда с листовыми узлами необходимо проделать действия, не меняя при этом графа. Такие действия проводят под окружением no_grad, которое блокирует создание новых узлов графа. Так, в примере ниже под тензор x память выделяется только один раз (для больших тензоров это важно). Затем в цикле под no_grad происходит изменение значений в этой памяти и дальше строится граф. Так как листовой тензор x не пересоздаётся, у него необходимо обнулить градиенты иначе они начнут суммироваться на следующих итерациях цикла:

x = empty(2).requires_grad_(True)

for i in range(1,3):
    with torch.no_grad():                  # disabled gradient calculation
        x.fill_(i)                         # меняем существующий 
        
    z = x.dot(x)
    z.backward()                           # вычислительный граф
    
    print(z.item(), x.grad.numpy())    
    
    x.grad.zero_()                         # обнуляем градиенты

Этот и предыдущий пример приведут к одинаковым результатам:

2.0  [2., 2.]
8.0  [4., 4.]

Другой способ изменения данных тензора, без изменения вычислительного графа, это непосредственная работа с его атрибутом data. Так, выше можно было бы написать:

for i in range(1,3):
    x.data.fill_(i)                         # меняем существующий 
...

После окончания окружения with с методом torch.no_grad(), построение графа включится само. Это же можно сделать руками при помощи метода torch.enable_grad():

x = ones(1, requires_grad=True)
with torch.no_grad():                      # отключаем построение графа
    z1 = 2 * x
    with torch.enable_grad():              # включаем  построение графа 
        z2 = 2 * x
print(x.requires_grad, z1.requires_grad, z2.requires_grad)  # True False True

Пример вычислений в цикле для поиска оптимальных параметров линейной модели можно найти в этом документе.

Отсоединение узла от графа

При помощи метода detach можно получит "отсоединенный" от графа тензор, который будет ссылаться на данные исходного узла, но не быть частью графа:

x = tensor([1.,2.], requires_grad=True)   
y = x.detach()                                

print(x)                                   # tensor([1., 2.], requires_grad=True)
print(y)                                   # tensor([1., 2.])
y[0]=5 
print(x)                                   # tensor([5., 2.], requires_grad=True)

Это альтернативный к окружению no_grad() способ изменения листовых узлов без изменения графа:

x  = empty(2).requires_grad_(True)
xd = x.detach()
 
for i in range(1,3):
    xd.fill_(i)
         
    z = x.dot(x)                   # начинаем строить граф
    z.backward()                   # вычислительный граф
     
    print(z.item(), x.grad)
     
    x.grad.zero_()                 # обнуляем градиенты

Немного примеров

Рассмотрим пример в котором при прямом проходе получается одно и тоже значение, однако градиенты оказываются различными, в зависимости от способов формирования переменной y:

x  = tensor(3.).requires_grad_(True)   #   x.grad y.grad  y.requires_grad
y  = tensor(3.).requires_grad_(True)   # A:  1    6       True  
#y = x                                 # B:  7    7       True  
#y = tensor(1.)                        # C:  1    None    False 
#y = x.detach().clone()                # D:  1    None    False
#y = x.clone()                         # E:  7    None    True, grad_fn=<CloneBackward>

z = x + y*y                            # z = 12
z.backward()

Случай A: производные вычисляются по двум независимым переменным $z=z(x,y)=x+y^2$. Это приводит к градиентам: $\nabla_x\, z(x,y) = 1$ и $\nabla_y\, z(x,y) = 2y$.
Случай B: присвоение y=x происходит по ссылке и переменная y является просто "другим обозначением" x. Поэтому $z=z(x)=x+x^2$ и $\nabla_x\, z(x) = 1+2x$ (в $y$ будет такой же градиент).
Случаи С, D эквивалентны. В методе torch.tensor(1.) создаётся тензор без requires_grad, поэтому для графа это константа. Аналогично, x.clone() делает копию x, которая затем методом detach "отсоединяется" от графа (ниже она снова присоединится, но уже как константа).
Случай E чуть более сложный и наименее осмысленный. Метод x.clone() делает копию x. Эта операция является узлом графа. При обратном проходе в листовом узле сойдутся два градиента (от сложения и от операции клонирования), которые сложившись дадут 7.

На самом деле клонирование без отсоединения иногда приводит к не самому ожидаемому результату, поэтому под графом при клонировании обычно стоит делать detach().clone() или вызывать его под окружением no_grad:

x = torch.ones(1, requires_grad=True)
                               # y.requires_grad:  y.grad_fn:
with torch.no_grad():          
    y = x.clone()              # False             None
y = x.detach().clone()         # False             None
y = x.clone()                  # True              <CloneBackward>

Что нельзя делать с листьями

В PyTorch стартовые (листовые) переменные по которым вычисляют градиент не должны участвовать в in-place вычислениях и их нельзя перезаписывать. Рассмотрим эти ограничения подробнее.

Напомним, что in-place операции меняют значение переменной не создавая новой памяти. В PyTorch такими являются все методы с подчёркиванием в конце имени: fill_(), add_(), mm_() и т.д. Ниже в последней строке происходит не in-place вычисление (результат x+1 записывается в новую память - см. значение id():

x = ones(1);    print(x, id(x))   # tensor([1.]) 2769629314008

x += 1;         print(x, id(x))   # tensor([2.]) 2769629314008   in-place
x.add_(1);      print(x, id(x))   # tensor([3.]) 2769629314008   in-place
x = x + 1;      print(x, id(x))   # tensor([4.]) 2769629311928   non in-place

Следующий код приведёт к ошибке "a leaf Variable that requires grad has been used in an in-place operation":

x = tensor(1., requires_grad=True)
x += 1                             # in-place для листа запрещён!

Та же ошибка возникнет в следующем коде (y получает ссылку на x, поэтому это и есть x):

x = ones(1.,requires_grad=True); print(x,id(x)) # tensor(1.,requires_grad=True) ...95208
y = x                          ; print(y,id(y)) # tensor(1.,requires_grad=True) ...95208
y *= 1                                          # in-place для листа

Для нелистовых узлов использовать in-place вычисления можно:

x = tensor(1.,requires_grad=True)   # x.grad = tensor(0.5)
y = 2*x                             # tensor(2.,     grad_fn=<MulBackward0>)
y += 2                              # tensor(4.,     grad_fn=<AddBackward0>)
y.log_()                            # tensor(1.3863, grad_fn=<LogBackward> )
y.backward()                        # y = log(2*x+2); y'=1/(x+1)

Листовая переменная не должна переприсваиваться, потому, что она будет "уничтожена" и потеряет свойство requires_grad:

x = tensor(1., requires_grad=True) #  tensor(1., requires_grad=True)
x = x + 1                          #  tensor(2., grad_fn=<AddBackward0>) нет requires_grad

Срезы теноров

Срезы (slice) тензоров возвращают новый тензор, с частью данных исходного. При этом они используют для хранения данных общую память. Поэтому вычисление градиентов на графах с функциями срезов требует определённой аккуратности:

x = tensor(1., requires_grad=True)    
s = ones(2)
s[1] =  s[0] * x                      # s[1] =  s[0].clone() * x <- так надо!!!
z = s.sum()                           # z = s[0] + s[0]*x
z.backward()

Этот код приведёт к ошибке: "one of the variables needed for gradient computation has been modified by an inplace operation". Чтобы её устранить, необходимо сделать копию тензора-элемента: s[1] = s[0].clone() * x. При этом должен использоваться именно метод clone(): "Unlike copy_(), this function is recorded in the computation graph. Gradients propagating to the cloned tensor will propagate to the original tensor." В частности на графе у тензора s имеем: s.grad_fn=<CopySlices>.

Присвоение в срез является in-place операцией, поэтому запрещена для листьев. Следующий код приведёт к ошибке:

x, w = torch.randn(1), torch.randn(1, requires_grad=True)
w[0] = 1.
y = x*w
y.backward()

Наконец, срезы могут существенно замедлять обратное распространение градиента. Ниже два кода выполняют одинаковые вычисления, однако правый код работает почти в 10 раз медленнее:

y = []       
for i in range(100):
    x = torch.randn(1,256,256, 
                    requires_grad=True)
    y.append( x )        
y = torch.cat(y, dim=0)
z = y.sum()
z.backward()

y = torch.empty(100,256,256)        
for i in range(100):
    x = torch.randn(256,256, 
                    requires_grad=True)
    y[i] = x   
    
z = y.sum()
z.backward()

Если закомментировать z.backward(), то время вычисления станет сравнимым.

Таким образом, при работе с вычислительными графами, стоит избегать слайс-копирований, приводящих к grad_fn=<CopySlices>

Визуализация

Для визуализации вычислительных графов можно использовать небольшую библиотеку torchviz (см. её документацию и примеры):

import torchviz
from torch import tensor, empty, ones, zeros

w, b = ones(5, requires_grad=True), tensor(0., requires_grad=True)
x = ones(5)
z = x.dot(w) + b

torchviz.make_dot(z,  params = {'x': x, 'w': w, 'b': b} )

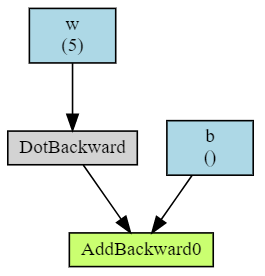
Обратим внимание, что библиотека рисует только листовые узлы для которых установлено requires_grad=True.

Минимизация функции

Приведём пример минимизации функции нескольких переменных при помощи градиентного метода. Для этого воспользуемся стандартным оптимайзером SGD:

import torch

def fun(x):    
    return x[0]**2 + (x[1]-1)**2

x = torch.tensor([1.,2.], requires_grad=True)    # начальные значения

optimizer = torch.optim.SGD([x],  lr=1, momentum=0.5) 
for it in range(20):
    optimizer.zero_grad()                        # обнуляем градиенты  
    y = fun(x)                                   # вычисляем значения функции
    y.backward()                                 # вычисляем градиенты     
    optimizer.step()                             # подправляем параметры
    
    print(y.item(), x.detach().numpy())