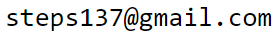ML: Вычислительный граф
Введение
Машинное обучение обычно сводится к минимизации скалярной функции,
зависящей от множества переменных.
Простейшим примером является линейная модель
$\mathbf{y} = \mathbf{x}\cdot\mathbf{w} + \mathbf{b}$
с параметрами $\mathbf{w}$ (матрица) и $\mathbf{b}$ (вектор).
По набору обучающих примеров $\{\hat{\mathbf{x}},\hat{\mathbf{y}}\}$
вычисляется ошибка обучения $L$. Для mse-ошибки (mean squared error)
она равна среднему значению квадрата разности обучающих значений $\hat{\mathbf{y}}$
и выходов модели $\mathbf{y}$:
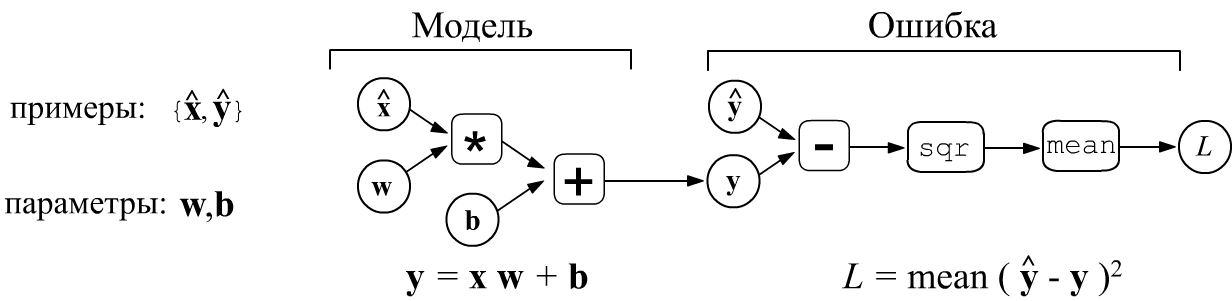
Ошибка модели зависит от её параметров $L=L(\mathbf{w},\mathbf{b})$. Обучение модели означает поиск значений параметров при которых ошибка достигает своего минимума: $\mathbf{w},\,\mathbf{b} = \text{argmin}\,L(\mathbf{w},\,\mathbf{b})$. Если параметров очень много, наиболее эффективен градиентный метод и различные его модификации. Для сложной модели аналитически вычислить градиент (производные по параметрам) непросто. Удобнее представить модель в виде вычислительного графа (computational graph). Граф имеет топологию дерева, корень которого - это искомая величина (ошибка $L$), а узлы выполняют элементарные вычисления. Если производные в каждом узле известны, то можно найти и градиент ошибки по параметрам модели, которые находятся в листьях дерева. Подобный подход лежит в основе всех современных фреймворков машинного обучения.
Общая постановка задачи
Пусть модель задана функцией $\mathbf{y}=f(\mathbf{x},\,\mathbf{p})$,
где $\mathbf{x}$ - вектор признаков объекта,
а $\mathbf{p}$ - вектор параметров.
Кроме этого, есть $N$ обучающих примеров
$\{\hat{\mathbf{x}},\,\hat{\mathbf{y}}\}=(\hat{\mathbf{x}}^{(1)},\,\hat{\mathbf{y}}^{(1)}),\,...,\,(\hat{\mathbf{x}}^{(N)},\,\hat{\mathbf{y}}^{(N)})$,
которые помечаются шляпкой.
Параметры $\mathbf{p}$ модели подбираются так, чтобы минимизировать среднюю ошибку $L$ на один пример:
$$
L ~=~ L(\mathbf{p})~=~ \frac{1}{N}\sum^N_{i=1} L(\hat{\mathbf{y}}^{(i)},\,\mathbf{y}^{(i)}),~~~~~~~~~~~
\mathbf{y}^{(i)} = f(\hat{\mathbf{x}}^{(i)},\mathbf{p}).
$$
Чтобы найти минимум $L$, необходимо сдвигать вектор параметров в направлении обратном к градиенту (частным производным)
$L$ по $\mathbf{p}$. Величина сдвига определяется скалярным гиперпараметром $\lambda$ (скорость обучения):
Вычисления проводятся в два этапа. Сначала при прямом проходе (слева-направо)
вычисляется ошибка $L$ при заданных $\hat{\mathbf{x}}$, $\hat{\mathbf{y}}$ и $\mathbf{p}$.
При этом определённые значения принимают все узлы вычислительного графа.
Затем запускается процедура обратного прохода.
Начальный градиент $g$ в скалярном узле ошибки $L$ является скаляром.
Проходя через узлы графа от ошибки справа-налево, он превращается в вектор $\mathbf{g}$ (в общем случае в тензор).
Изменения $\mathbf{g}$ на каждом узле происходят таким образом, что,
когда он "добирается" до параметров $\mathbf{p}$,
то оказывается равным частным производным: $\mathbf{g}^{(\mathbf{p})}=\partial L/\partial\mathbf{p}$.
Прямой и обратный проходы
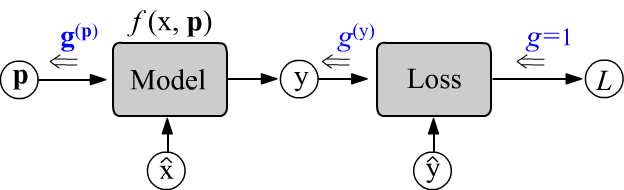
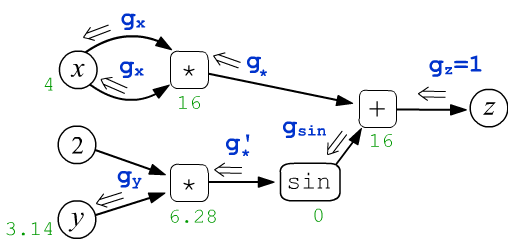
Рассмотрим в качестве простого примера функцию $z=f(x,y)=x\cdot x + \sin(2 y)$ двух скалярных переменных $x$ и $y$. Пусть $x=4$ и $y=3.14159$. Эти числа присваиваются в листовые узлы $x,y$ и затем распространяются по вычислительному графу слева-направо. Так, в узел умножения входят две стрелки каждого аргумента операции. В первом таком узле они "несут" одинаковые значения $4$, которые перемножаясь, дают на выходе узла число $16$ (зелёный цвет). В результате, каждый узел, включая финальный ($z=16$), принимает определённое значение:
$$ z = x\cdot x + \sin(2\cdot y) $$
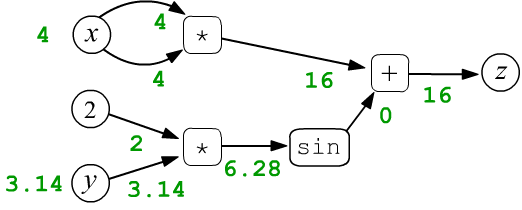
После прямого прохода по графу, запускается обратное (backward) распространение вычисления производных. Ниже на рисунке из корневого узла $z$ выходит число $g_z$ (его полагают равным $1$). Оно движется по графу к листовым узлам $x,y$. Проходя через каждый узел эта величина определённым образом изменяется:
$$ \begin{array}{lcl} g_x = \frac{\displaystyle\partial z}{\displaystyle\partial x} &=& 2\cdot x,\\[4mm] g_y = \frac{\displaystyle\partial z}{\displaystyle\partial y} &=& 2\,\cos(2\cdot y) \end{array} $$
Необходимо так определить правила этих изменений, чтобы входящие в листовые узлы $x,y$ величины $g_x, g_y$ оказались частными производными $z$ по $x,y$.
Спойлер
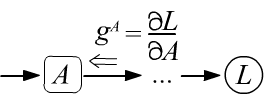 В этом документе встречается много громоздких формул. Чтобы не потеряться в них,
перечислим сначала основные правила обратного распространения:
В этом документе встречается много громоздких формул. Чтобы не потеряться в них,
перечислим сначала основные правила обратного распространения:
- Входящий в любой узел $A$ градиент $g^A$, имеет смысл производной целевой величины (корня дерева) по значению в этом узле: $g^A = \partial L/\partial A$.
- Тензорная размерность градиента, входящего в узел,
совпадает с размерностью
тензора, получаемого этим узлом на его выходе.
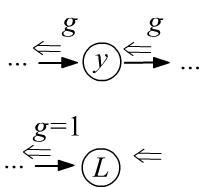
- Через узлы переменных градиент проходит без изменений, а в узлы констант "не заходит".
- Начальный градиент, входящий и выходящий из корня дерева $L$
равен единице,
так как по определению это: $g=\partial L/\partial L =1$. - Пройдя через узел, градиент расщепляется по всем входящим в узел рёбрам и умножается на производные между узлами, которые связывает ребро (ниже левый рисунок).
- Если в узел входит несколько градиентов, то они складываются (ниже правый рисунок), что является следствием правила вычисления производной от сложной функции (формула под рисунком).
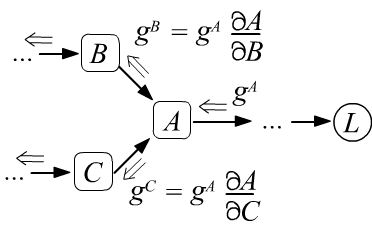 $$
g^B ~=~ \frac{\partial L}{\partial B} ~=~ \frac{\partial L}{\partial A}\,\frac{\partial A}{\partial B} ~=~ g^A\,\frac{\partial A}{\partial B},
$$
$$
g^B ~=~ \frac{\partial L}{\partial B} ~=~ \frac{\partial L}{\partial A}\,\frac{\partial A}{\partial B} ~=~ g^A\,\frac{\partial A}{\partial B},
$$
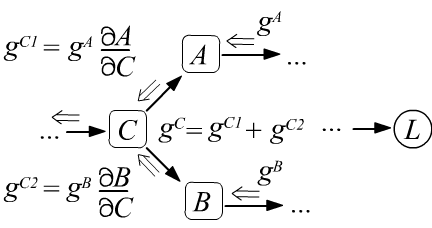 $$
g^C ~=~ \frac{\partial L}{\partial C} ~=~
\frac{\partial L}{\partial A}\,\frac{\partial A}{\partial C}
+
\frac{\partial L}{\partial B}\,\frac{\partial B}{\partial C}
~=~ g^A\,\frac{\partial A}{\partial C} + g^B\,\frac{\partial A}{\partial B}.
$$
$$
g^C ~=~ \frac{\partial L}{\partial C} ~=~
\frac{\partial L}{\partial A}\,\frac{\partial A}{\partial C}
+
\frac{\partial L}{\partial B}\,\frac{\partial B}{\partial C}
~=~ g^A\,\frac{\partial A}{\partial C} + g^B\,\frac{\partial A}{\partial B}.
$$
Производные для скаляров
Рассмотрим сначала скалярные функции одной $f(x)$ и двух $f(x,y)$ переменных. В узлы которые их вычисляют входит одно и два ребра соответственно (аргументы функции). Пусть при обратном распространении в узел функции справа-налево попадает некоторое число $g$. Потребуем что-бы на выходе оно изменялось следующим образом:
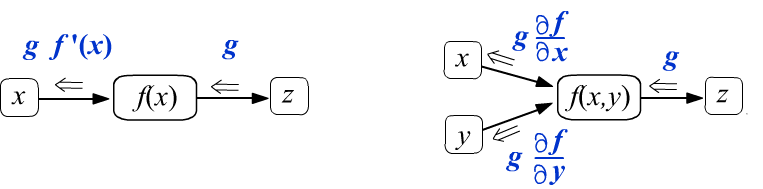
(def1)
Проходя через узел, вычисляющий $f(x)$, величина $g$ умножается на производную функции $f'(x)$.
Аналитическое выражение для $f'(x)$ известно, т.к. предполагается, что функция узла вычислительного графа
достаточно простая.
Числовые значения $f(x)$ и $f'(x)$ зависят от значения аргумента $x$,
известного в результате прямого прохода по графу (слева направо).
Аналогичная ситуация для функции двух переменных.
Если граф состоит только из этих узлов, то при начальном градиенте $g=1$, мы получим правильные выражения для производных, входящих в листовые узлы $x,y$.
Применим эти определения к функции синуса и операциям сложения и умножения:
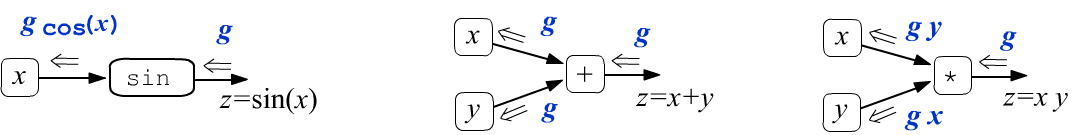
Таким образом, операция сложения не меняет проходящей через него градиент $g$, расщепляется его на две одинаковых величины. Проходя через узел умножения, градиент изменяется, умножаясь на "другой" аргумент.
Теперь несложно записать распространение производных для функции $z=x*x+\sin(2*y)$:
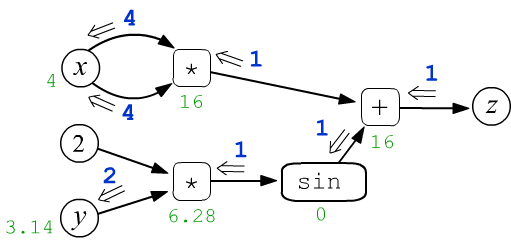
где учтено, что $\cos(2\pi)=1$. Таким образом, в узел $y$ входит двойка ($\partial z/\partial y = 2$), а в узел $x$ входит два раза четвёрка, т.е. $\partial z/\partial x = 8$.
Приведём пример вычисления этих градиентов на PyTorch:
from torch import tensor, sin x, y = tensor(4., requires_grad=True), tensor(3.14159265, requires_grad=True) z = x*x + sin(2*y) # граф с корнем: tensor(16., grad_fn=<AddBackward0>) z.backward() # запускаем вычисление градиентов (обратный проход) print(x.grad, y.grad) # tensor(8.) tensor(2.)В этом коде на Python вводятся два тензора $x,y$ нулевой размерности (скаляры). Свойство requires_grad означает, что эти тензоры будут листьями дерева вычисления. В результате записи выражения для $z$ (корень), это дерево непосредственно строится и одновременно с этим запускается прямой проход (вычисляется значение $z$). Вызов метода backward инициирует обратный проход, в результате которого, у $x,y$ появляется свойство grad, в котором находятся значения производных $\partial z/\partial x$ и $\partial z/\partial y$.
Граф для составных функций
Рассмотрим в качестве примера обратное распространение для составных функций. Ниже слева $z$ равна функции $A$, которая зависит от функции $B(x)$. Производная $z$ по $x$ берётся как производная сложной функции (формула под рисунком). К этому же результату мы прийдём анализируя обратное распространение производной по графу. Из узла $z$ выходит единица. Заходя в узел $B$ она превращается в $\partial A/\partial B$. После прохождения узла $B$ эта производная умножается на $\partial B/\partial x$:
 $$
g^x ~=~ \frac{\partial z}{\partial x} ~=~ \frac{\partial A}{\partial x} ~=~ \frac{\partial A}{\partial B}\,\frac{\partial B}{\partial x},
$$
$$
g^x ~=~ \frac{\partial z}{\partial x} ~=~ \frac{\partial A}{\partial x} ~=~ \frac{\partial A}{\partial B}\,\frac{\partial B}{\partial x},
$$
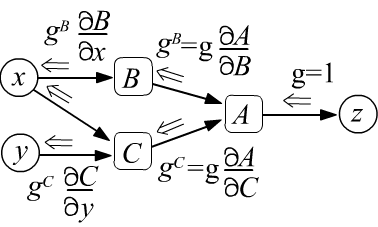 $$
g^x ~=~ \frac{\partial z}{\partial x} ~=~ \frac{\partial A}{\partial x} ~=~
\frac{\partial A}{\partial B}\,\frac{\partial B}{\partial x} ~+~
\frac{\partial A}{\partial C}\,\frac{\partial C}{\partial x}.
$$
$$
g^x ~=~ \frac{\partial z}{\partial x} ~=~ \frac{\partial A}{\partial x} ~=~
\frac{\partial A}{\partial B}\,\frac{\partial B}{\partial x} ~+~
\frac{\partial A}{\partial C}\,\frac{\partial C}{\partial x}.
$$
Аналогично анализируется второй пример. В нём поток градиента расщепляется на узле $A$, а затем сходится на листе дерева $x$. Эти две производные необходимо просуммировать, что соответствует знаку плюс в формуле частной производной (под рисунком).
Градиенты для тензоров
В задачах машинного обучения корнем графа (дерева) обычно является скалярная величина (например ошибка модели), тогда как листовые узлы графа (параметры модели) - это тензоры. Частные производные корня по компонентам тензора собственно и называются градиентами.
 Пусть из скалярной функции ошибки $L$ на вход модели поступает градиент.
Он распространяется по графу и
входит в виде тензора $g^{(\mathbf{Z})}_{ij...}$ справа в некоторый узел $\mathbf{Z}$.
В этом узле происходит вычисление, меняющее тензор на $g^{(\mathbf{X})}_{\alpha\beta...}$
и он входит в узел $\mathbf{X}$.
Пусть из скалярной функции ошибки $L$ на вход модели поступает градиент.
Он распространяется по графу и
входит в виде тензора $g^{(\mathbf{Z})}_{ij...}$ справа в некоторый узел $\mathbf{Z}$.
В этом узле происходит вычисление, меняющее тензор на $g^{(\mathbf{X})}_{\alpha\beta...}$
и он входит в узел $\mathbf{X}$.
В зависимости от характера вычислений в $Z$, число индексов и их размерности тензора могут измениться. При этом размерность и форма градиента, входящего в узел всегда должны совпадать с размерностью и формой данных которые хранятся в этом узле. Так как $L$ зависит от тензора $\mathbf{Z}$, который зависит от тензора $\mathbf{X}$, то производная сложной функции вычисляется следующим образом:
(def2)
Если корнем вычислительного графа выступает скалярная величина, то выходящий из неё градиент, как и раньше, полагают равным 1, т.к. $\partial L/ \partial L = 1$.
☯ Приведенное определение можно обобщить на случай, когда в корне графа находится тензор, а не скаляр. В зависимости от целей, градиент в нём инициализируют тем или иным тензором (той-же размерности!). Например, если это тензор состоит из единиц: $g^{(\mathbf{L})}_{ij...}=g^{(\mathbf{Z})}_{ij...}=1$, то будет происходить суммирование всех компонент корневого тензора, что превратит его в скаляр:
$$ g^{(\mathbf{X})}_{\alpha\beta...} ~=~ \sum_{i,j,...} \frac{\partial Z_{ij...}}{\partial X_{\alpha\beta...}} ~=~ \frac{\partial Z}{\partial X_{\alpha\beta...}},~~~~~~~~~~~~~~~Z~=~\sum_{i,j,...} \,Z_{ij...} $$Чтобы получить частную производную непосредственно от компонент $Z_{ij...}$, необходимо взять $g^{(\mathbf{Z})}_{ij...}$ состоящим из нулей, кроме единственного элемента с индексами $i,j,...$, равного единице (проекционный тензор). Впрочем для машинного обучения эти случаи не важны.
Сложение и умножение тензоров
Выясним как градиент изменяется при прохождении через различные вычислительные узлы. Предварительно стоит просмотреть напоминание по работе с символом Кронекера $\delta_{ij}$ в этом документе.
✒ Простейший узел складывает два тензора с одинаковым числом индексов. Воспользовавшись определением (def2), имеем:
$$ Z_{ij...} = X_{ij...} + Y_{ij...}, ~~~~~~~~~~~~~ g^{(\mathbf{X})}_{\alpha\beta...} ~=~ \sum_{ij...} g^{(\mathbf{Z})}_{ij...}\,\frac{\partial Z_{ij...}}{\partial X_{\alpha\beta...}} ~=~ \sum_{ij...} g^{(\mathbf{Z})}_{ij...}\,\delta_{i\alpha}\,\delta_{j\beta}... ~=~ g^{(\mathbf{Z})}_{\alpha\beta...} $$
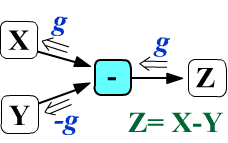 Таким образом, суммирование не меняет градиента,
расщепляя его на два одинаковых тензора, которые попадают в узлы каждого аргумента операции.
При вычитании $Z_{ij...} = X_{ij...} - Y_{ij...}$
градиент, входящий в узел Y изменит свой знак,
а градиент в узел X попадёт без изменения.
Таким образом, суммирование не меняет градиента,
расщепляя его на два одинаковых тензора, которые попадают в узлы каждого аргумента операции.
При вычитании $Z_{ij...} = X_{ij...} - Y_{ij...}$
градиент, входящий в узел Y изменит свой знак,
а градиент в узел X попадёт без изменения.
✒ Если $\mathbf{M}$ - матрица формы (n,m), а $\mathbf{v}$ - вектор с m компонентами, то при их сложении происходит расширение (broadcasting) вектора $\mathbf{v}$: (n,m)+(m,) = (n,m)+(1,m) = (n,m). В этом случае градиент $\mathbf{g}^{(\mathbf{v})}$, входящий в узел векторного аргумента $\mathbf{v}$, также является вектором:
$$ Z_{ij} = M_{ij} + v_j, ~~~~~~~~~~~~~~~~~ g^{(\mathbf{v})}_{\alpha} = \sum_{i,j} g^{(\mathbf{Z})}_{ij}~\frac{\partial Z_{ij}}{\partial v_{\alpha}} ~=~ \sum_{i,j} g^{(\mathbf{Z})}_{ij}~\delta_{j\alpha} ~=~ \sum_i \,g^{(\mathbf{Z})}_{i\alpha}. $$В матричный аргумент $M_{ij}$ узла сложения градиент $g^{(\mathbf{Z})}_{ij}$, как и раньше, попадает без изменения. В общем случае суммирование производится по всем индексам, которые подверглись процедуре расширения.
✒ Узел умножения тензоров (без свёртки) рассмотрим на примере двух матриц:
$$ Z_{ij} = M_{ij}\,N_{ij},~~~~~~~~~~~~~~~ g^{(\mathbf{M})}_{\alpha\beta} = \displaystyle\sum_{ i,j} g^{(\mathbf{Z})}_{ij}~\frac{\partial Z_{ij}}{\partial M_{\alpha\beta}} = \displaystyle\sum_{i,j} g^{(\mathbf{Z})}_{ij}~\delta_{i\alpha}\delta_{i\beta}\, N_{ij} = \displaystyle g^{(\mathbf{Z})}_{\alpha \beta}\, N^{\phantom{(\mathbf{Z})}}_{\alpha\beta} $$и аналогично для $g^{(\mathbf{N})}_{\alpha\beta}$ Таким образом, изменение градиента полностью аналогично изменению производных скалярных величин при прохождении узла их произведения.
Свёртка тензоров
✒ Рассмотрим свёртку двух векторов в узле dot. Её результатом будет скаляр, поэтому и в узел входит скаляр $g^{(z)}$:
$$ z = \sum_i u_i\,v_i,~~~~~~~~~~~~~~ g^{(\mathbf{u})}_\alpha = g^{(z)}\, \displaystyle\frac{\partial z}{\partial u_{\alpha}} = g^{(z)}\,v_{\alpha}, $$и аналогично для $g^{(\mathbf{v})}_{\alpha} $ Таким образом, при обратном распространении в узел dot попадает скаляр $g^{(z)}$, а при выходе из него он превращается в два вектора: $\mathbf{g}^{(\mathbf{u})} = \mathbf{g}^{(z)} \, \mathbf{v}$ и $\mathbf{g}^{(\mathbf{v})} = \mathbf{g}^{(z)} \, \mathbf{u}$.
✒ Свёртка матрицы $M_{ij}$ и вектора $v_j$, в фреймворке PyTorch,
обозначается как mv.
Результатом операции будет вектор, поэтому
и входящий в узел градиент будет вектором $g^{(\mathbf{z})}_{i}$:
Вторая формула - это просто свёртка вектора и матрицы: $\mathbf{g}^{(\mathbf{v})} = \mathbf{g}^{(\mathbf{z})}\,\mathbf{M}$.
✒ Вычисления для свёртки двух матриц (результат снова матрица) проводится аналогичным образом:
$$ Z_{ij} = \sum_{k} M_{ik}\,N_{kj},~~~~~~~~~~~~~~~ \left\{ \begin{array}{lclclcl} g^{(\mathbf{M})}_{\alpha\beta} &=& \displaystyle\sum_{ i,j} g^{(\mathbf{Z})}_{ij}~\frac{\partial Z_{ij}}{\partial M_{\alpha\beta}} &=& \displaystyle\sum_{i,j,k} g^{(\mathbf{Z})}_{ij}~\delta_{i\alpha}\delta_{k\beta}\, N_{kj} &=& \displaystyle\sum_{j} \displaystyle g^{(\mathbf{Z})}_{\alpha j}\, N^{\phantom{(\mathbf{Z})}}_{\beta j}, \\[3mm] g^{(\mathbf{N})}_{\alpha\beta} &=& \displaystyle\sum_{i,j} g^{(\mathbf{Z})}_{ij}~\frac{\partial Z_{ij}}{\partial N_{\alpha\beta}} &=& \displaystyle \sum_{i,j,k} g^{(\mathbf{Z})}_{ij}~M_{ik}\,\delta_{k\alpha}\delta_{j\beta} &=& \displaystyle \sum_{i} M^{\phantom{(\mathbf{Z})}}_{i\alpha}\,g^{(\mathbf{Z})}_{i\beta}. \end{array} \right. $$ Переставляя индексы в матрице при помощи операции транспонирования $M^\top_{\alpha\beta}=M_{\beta\alpha}$, эти формулы можно записать в безындексной форме: $~~\mathbf{g}^{(\mathbf{M})}= \mathbf{g}^{(\mathbf{Z})}\,\mathbf{N}^\top~~$ и $~~\mathbf{g}^{(\mathbf{N})}= \mathbf{M}^\top\,\mathbf{g}^{(\mathbf{Z})}$.
Представим, полученные выше формулы в графическом виде, опуская индексы у матриц и векторов:

Пример вычисления градиента от скалярного произведения двух векторов $z=\mathbf{u}\cdot \mathbf{v}$, для которого $\partial z/\partial \mathbf{u} = \mathbf{v}$:
u, v = tensor([1.,2.], requires_grad=True), tensor([3.,4.], requires_grad=True) z = u.dot(v) # tensor(11., grad_fn=<DotBackward>) z.backward() # запускаем вычисление градиентов print(u.grad) # tensor([3., 4.]) print(v.grad) # tensor([1., 2.])
Функции от тензоров
Рассмотрим теперь функции от тензора. Если это "обычная" функция, применяемая независимо к каждому элементу тензора, то всё как и в скалярном случае:
$$ Z_{ij...} = f(X_{ij...}),~~~~~~~~~~ g^{(\mathbf{X})}_{\alpha\beta...} ~=~ \sum_{i,j,...} g^{(\mathbf{Z})}_{ij...}~\frac{\partial f(X_{ij...})}{\partial X_{\alpha\beta...}} ~=~\sum_{i,j,...} g^{(\mathbf{Z})}_{ij...}~f'(X_{ij...})~\delta_{i\alpha}\delta_{j\beta}... ~=~ g^{(\mathbf{Z})}_{\alpha\beta...}~f'(X_{\alpha\beta...}). $$ Наиболее популярные в нейронных сетях функции имеют следующие производные: $$ \left\{ \begin{array}{rcl} y=\sigma(x)&=&\displaystyle\frac{1}{1+e^{-x}},\\[3mm] \sigma'(x)&=& y\,(1-y) \end{array} \right. ~~~~~~~~~~~~~ \left\{ \begin{array}{rcl} y=\tanh(x) &=& \displaystyle\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\\[3mm] \tanh'(x) &=& 1-y^2 \end{array} \right. ~~~~~~~~~~~~~ \left\{ \begin{array}{rcl} y=\text{relu}(x) &=& \text{max}(0,\,x)\\[3mm] \text{relu}'(x) &=& \mathrm{0~if~x~<~0~else~1} \end{array} \right. $$Чуть сложнее с функциями, которые меняют размерность тензора. Рассмотрим например, суммирование тензора по первому индексу: X.sum(axis=0):
$$ Z_{jk...} = \sum_i X_{ijk...},~~~~~~~~~~ g^{(\mathbf{X})}_{\alpha\beta\gamma...} ~=~ \sum_{j,k,...} g^{(\mathbf{Z})}_{jk...}~\frac{\partial Z_{jk...}}{\partial X_{\alpha\beta\gamma...}} ~=~ \sum_{i,j,k,...} g^{(\mathbf{Z})}_{jk...}~\delta_{i\alpha}\delta_{j\beta}\delta_{k\gamma}\,... ~=~ g^{(\mathbf{Z})}_{\beta\gamma...} $$Таким образом, для каждого значения индекса $\alpha$ в $g^{(\mathbf{X})}_{\alpha\beta\gamma...} $ происходит дублирование входящего в функцию градиента $g^{(\mathbf{Z})}_{\beta\gamma...}$. Когда суммируются все компоненты тезора $\mathbf{X}$, входящий в него градиент (той же размерности) из узла суммирования будет состоять из единиц, умноженных на входящий в узел скалярную величину $g^{(Z)}$.
x = 5*torch.eye(2,3) # [ [5., 0., 0.],
x.requires_grad=True # [0., 5., 0.] ]
z = x.sum()
z.backward() # запускаем вычисление градиентов
print(x.grad) # [ [1., 1., 1.],
# [1., 1., 1.] ]
Софтмакс и ошибка по кросс-энтропии
В задачах классификации часто используют ошибку кросс-энтропии (CE, CrossEntropyLoss) перед которой стоит функция softmax. Эти два вычислительных узла являются стартовыми при обратном распространении градиента.
Функция softmax: $\mathbf{y}=\text{sm}(\mathbf{x})$ нормирует вектор $\mathbf{x}$, так, чтобы сумма компонент вектора $\mathbf{y}$ на выходе функции была равна единице (обычно $y_i$ интерпретируются как вероятности классов).
$$ y_i = \frac{e^{x_i}}{\sum_k e^{x_k}},~~~~~~~~~~~~~~~~~~~~~~y_i > 0,~~~~~~\sum_k y_k = 1, ~~~~~~~~~~~~~~~ \frac{\partial y_i}{\partial x_\alpha} = y_i\,\delta_{i\alpha}\ - y_i\, y_\alpha. $$ Отметим, что софтмакс $\mathbf{y}=\text{sm}(\mathbf{x})$ неоднозначная функция. Если к каждой компоненте вектора $\mathbf{x}$ добавить одно и тоже число, то результат функции не изменится: $\text{sm}(\mathbf{x}+a) = \text{sm}(\mathbf{x})$. Градиент, $\mathbf{g}^{(\mathbf{y})}$, проходя через софтмакс, преобразуется в градиент $\mathbf{g}^{(\mathbf{x})}$: $$ g^{(\mathbf{x})}_\alpha ~=~ \sum_{i}\,g^{(\mathbf{y})}_i\,\frac{\partial y_i}{\partial x_\alpha} ~=~ \Bigr(g^{(\mathbf{y})}_\alpha - \sum_i g^{(\mathbf{y})}_i y_{i}\Bigr)\,y_\alpha. $$Таким образом, из входящего в функцию $\mathbf{y} = \text{sm}(\mathbf{x})$ градиента $g^{(\mathbf{y})}_\alpha$ вычитается его "среднее" по всем компонентам с весами $y_i$ ("вероятности") и результат снова умножается на "вероятности": $\mathbf{g}^{(\mathbf{y})}\odot \mathbf{y} - (\mathbf{g}^{(\mathbf{y})}\mathbf{y})\,\mathbf{y}$.
Ошибка CE получает на вход "вероятности" классов $y_i$, вычисленные моделью
и номер истинного класса $c$.
В качестве ошибки выступает логарифм с обратным знаком от вероятности правильного класса.
Минимизация CE-ошибки - это задача максимизации значения "вероятности"
$y_c$ правильного класса (т.к. благодаря софтмаксу все $y_i > 0$ и их сумма равна единице, максимизация
$y_c$ минимизирует вероятности остальных классов):
$$
L=\text{CE}(\mathbf{y}, c) = -\log y_c,~~~~~~~~~~~~~~~~g^{(\mathbf{y})}_i=\frac{\partial L}{\partial y_i} = -\frac{\delta_{i c}}{y_c}
=\{0,...,0,\frac{-1}{y_c},0,...,0\}.
$$
Градиент $g^{(\mathbf{y})}_i$, выходящий из функции ошибки - это вектор с нулевыми компонентами, кроме $c$-той компоненты истинного класса. Далее, проходя через софтмакс, он превращается в: $$ g^{(\mathbf{x})}_\alpha ~=~ y_\alpha - \delta_{\alpha c} ~=~ \left\{ \begin{array}{ll} y_i & i \neq c, \\ y_c - 1 & i = c. \end{array} \right. $$ Если бы $x_\alpha$ были параметрами модели, то градиентый метод со скоростью обучения $\lambda$ подправлял бы их следующим образом: $$ x_\alpha \mapsto x_\alpha - \lambda\,g^{(\mathbf{x})}_\alpha = \left\{ \begin{array}{ll} x_\alpha - \lambda\, y_\alpha & \alpha\neq c \text{ - уменьшаем для неверных классов} \\[2mm] x_c + \lambda\, (1-y_c) & \alpha = c \text{ - увеличиваем для правильного класса} \end{array} \right. $$ Если "правильная вероятность" $y_c$ близка к единице (а остальные $y_i$, соответственно, к нулю), параметры $x_i$ перестают изменяться. На практике, естественно, вектор $\mathbf{x}$ является не параметром, а выходом модели. Поэтому, при обратном распространении градиент $g^{(\mathbf{x})}_i$ продолжает двигаться по узлам в начало графа (к его параметрам).
Мини-PyTorch
Наметим идею построения графа вычислений (детали можно найти в файле: ML_Comp_Graph.ipynb).
Создадим класс тензора, который будет хранить элементы в numpy массиве.
Синтаксис методов сделаем близким к синтаксису фреймворка PyTorch,
с обзором которого можно познакомиться по этому документу.
У класса Tensor определим конструктор и метод tensor который преобразует аргумент в экземпляр класса Tensor, если он им ещё не является:
import numpy as np
class Tensor:
def __init__(self, val, args=None, fn=None):
self.data = np.array(val) # хранимые данные
self.grad = None # градиент, входящий в узел
self.fn = fn # операция, вычисляемая узлом
self.args = args # список аргументов операции
def tensor(self, t): # для констант в выражениях
return t if isinstance(t, Tensor) else Tensor(t)
Основные операции с тензорами осуществляются при помощи библиотеки numpy. Кроме возвращения значения операции, запоминают имя функции и ссылки на её аргументы. Вызов t = self.tensor(t) делается, чтобы аргументом операции мог быть не только Tensor, но и константа в виде числа или массива numpy:
class Tensor: # продолжение
def add(self, t): # сложение
t = self.tensor(t)
return Tensor(self.data + t.data, [self, t], "add")
def sub(self, t): # вычитание
t = self.tensor(t)
return Tensor(self.data - t.data, [self, t], "sub")
def mul(self, t): # умножение без свёртки
t = self.tensor(t)
return Tensor(self.data * t.data, [self, t], "mul")
def dot(self, v): # скалярное произведение векторов
v = self.tensor(v)
return Tensor(np.dot(self.data, v.data), [self, v], "dot")
def mv(self, v): # свёртка матрицы и вектора
v = self.tensor(v)
return Tensor(np.dot(self.data, v.data), [self, v], "mv")
def mm(self, n): # свёртка матриц
n = self.tensor(n)
return Tensor(np.dot(self.data, n.data), [self, n], "mm")
Ключевой метод backward вычисления градиентов при обратном распространении по графу имеет вид:
class Tensor: # продолжение
def backward(self, grad = 1):
if self.grad is None:
self.grad = grad
else: # накапливаем входящие градиенты
self.grad += grad
if self.fn == "add": # сложение
self.args[0].backward( grad)
self.args[1].backward( grad)
elif self.fn == "sub": # вычитание
self.args[0].backward( grad)
self.args[1].backward(-grad)
elif self.fn in ["dot", "mul"]: # свёртка векторов или умножение тензоров
self.args[0].backward( grad * self.args[1].data)
self.args[1].backward( self.args[0].data * grad)
elif self.fn == "mv": # свёртка матрицы и вектора
self.args[0].backward( np.outer(grad, self.args[1].data))
self.args[1].backward( np.dot(grad, self.args[0].data))
elif self.fn == "mm": # свёртка двух матриц
self.args[0].backward( np.dot(grad, self.args[1].data.T))
self.args[1].backward( np.dot(self.args[0].data.T, grad))
Рассмотрим пример использования класса Tensor.
v = Tensor([1,2]) # создаём вектор
m = Tensor(np.eye(2)) # создаём единичную матрицу
n = Tensor(np.ones((2,2))) # создаём матрицу из единиц
z = m.mm(n).mv(v).dot(v) # строим вычислительный граф
z.backward() # вычисляем градиенты
print(z) # 9.0
print(v.grad) # [6. 6.]
print(m.grad) # [[3. 3.]
# [6. 6.]]
print(n.grad) # [[1. 2.]
# [2. 4.]]