ML: Введение в PyTorch: 3. Нейронные сети
Последовательность слоёв
В этом документе обсуждается создание и обучение нейронных сетей на библиотеке PyTorch, основы которой описаны здесь и здесь. Справочник по основным типам слоёв, ошибок и оптимизаторов находятся здесь.
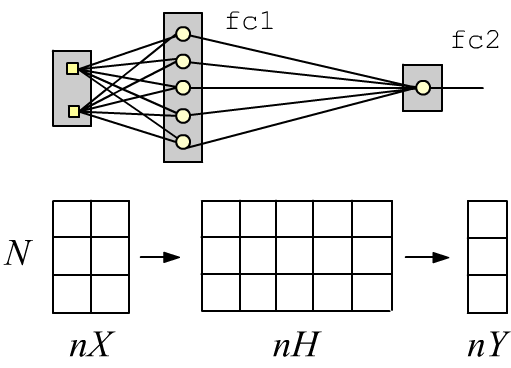
Простые нейронные сети с последовательной архитектурой можно создавать при помощи стопочного интерфейса. Например, двухслойная полносвязная сеть с двумя входами (nX=2 признака), одним (nY=1) сигмоидным выходом (2 класса) и пятью нейронами (nH=5) в скрытом слое имеет вид:
import torch
import torch.nn as nn
nX, nH, nY = 2, 5, 1
model = nn.Sequential(
nn.Linear(nX, nH), # первый слой
nn.Sigmoid(), # активация скрытого слоя
nn.Linear(nH, nY), # второй, выходной слой
nn.Sigmoid() ) # его активационная фу-я
Слой Linear делает линейное преобразование входного тензора формы (N, nX), где N - число примеров. На выходе слоя получается тензор формы (N, nH), который пропускается через сигмоид (новые nH признаков). Второй слой даёт тензор (N, nY) от которого также берётся через сигмоид. Если его значение меньше 0.5 - это первый класс, если больше 0.5 - второй.
Функциональная архитектура
При проектировании сложных нейронных сетей, их архитектуру удобнее задавать в функциональном виде.
Для этого создаётся наследник класса nn.Module.
В нём переопределяется конструктор и метод forward.
В конструкторе задаются необходимые слои и инициализируются их параметры.
Обратим внимание на вызов конструктора предка которому необходимо передать имя нашего класса.
В методе forward (прямое распространение) строится архитектура сети (слои связываются
в вычислительный граф):
class TwoLayersNet(nn.Module):
def __init__(self, nX, nH, nY):
super(TwoLayersNet, self).__init__() # конструктор предка с этим именем
self.fc1 = nn.Linear(nX, nH) # создаём параметры модели
self.fc2 = nn.Linear(nH, nY) # в полносвязных слоях
def forward(self, x): # задаётся прямой проход
x = self.fc1(x) # выход первого слоя
x = nn.Sigmoid()(x) # пропускаем через Sigmoid
x = self.fc2(x) # выход второго слоя
x = nn.Sigmoid()(x) # пропускаем через сигмоид
return x
model = TwoLayersNet(2, 5, 1) # экземпляр сети
Вызов nn.Line(in_features, out_features) создаёт два экземпляра линейного полносвязного слоя fc1, fc2 (fully connected). Одновременно с этим задаются случайные значения их весов и смещений. Скобочный оператор fc1(x) в методе forward запускает вычисления внутри слоя и на выходе выдаёт результирующий тензор.
Модельные данные
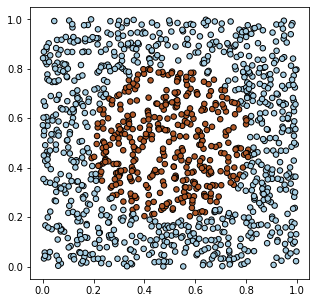Создадим на PyTorch модельные данные для объектов двух видов (два класса),
характеризующихся двумя признаками. Пусть на 2D плоскости
объекты первого класса заполняют единичный квадрат $[0...1]^2$, кроме круга в центре квадрата, где находятся
объекты второго класса:
X = torch.rand (1200,2) Y = (torch.sum((X - 0.5)**2, axis=1) < 0.1).float().view(-1,1)
При помощи библиотеки matplotlib нарисуем то, что в результате получилось:
import matplotlib.pyplot as plt # построение графиков
plt.figure (figsize=(5, 5)) # размеры (квадрат)
plt.scatter(X.numpy()[:,0], X.numpy()[:,1], c=Y.numpy()[:,0],
s=30, cmap=plt.cm.Paired, edgecolors='k')
plt.show() # выводим рисунок
Обучение сети
Для обучения сети необходимо создать функцию ошибки (то, что следует минимизировать) и оптимизатор (который будет минимизировать ошибку). Оптимизатору передаются параметры модели. В качестве ошибки выберем бинарную кросс-энтропию (BCELoss), а оптимизатором будет SGD (Stochastic Gradient Descent):
model = TwoLayersNet(2, 5, 1) # экземпляр сети
loss = nn.BCELoss()
optimizer = torch.optim.SGD(model.parameters(), # параметры модели
lr=0.5, momentum=0.8) # параметры оптимизатора
На каждой итерации из обучающих примеров формируется массив батчей,
запускается прямое распространение
y = model(bx) и
вычисляется ошибка loss (из сравнения выхода y модели с "правильными" значениями yb).
На вычислительном графе ошибки метод loss.backward() даёт
градиенты параметров модели, при помощи которых оптимизатор optimizer в методе step()
получает новые значения параметров:
def fit(model, X,Y, batch_size=100, train=True):
model.train(train) # важно для Dropout, BatchNorm
sumL, sumA, numB = 0, 0, int( len(X)/batch_size ) # ошибка, точность, батчей
for i in range(0, numB*batch_size, batch_size):
xb = X[i: i+batch_size] # текущий батч,
yb = Y[i: i+batch_size] # X,Y - torch тензоры
y = model(xb) # прямое распространение
L = loss(y, yb) # вычисляем ошибку
if train: # в режиме обучения
optimizer.zero_grad() # обнуляем градиенты
L.backward() # вычисляем градиенты
optimizer.step() # подправляем параметры
sumL += L.item() # суммарная ошибка (item из графа)
sumA += (y.round() == yb).float().mean() # точность определения класса
return sumL/numB, sumA/numB # средняя ошибка и точность
Функция fit делает проход по всем данным. Это называется эпохой обучения. Если параметр leran=True, то происходит обучение модели (изменение её параметров). Значение leran=False используется при оценке качества модели без её изменения. В качестве метрик качества используется средняя ошибка по всем примерам и средняя точность (доля правильно предсказанных классов). Обычно требуется достаточно много эпох обучения:
# режим оценки модели:
print( "before: loss: %.4f accuracy: %.4f" % fit(model, X,Y, train=False) )
epochs = 1000 # число эпох
for epoch in range(epochs): # эпоха - проход по всем примерам
L,A = fit(model, X, Y) # одна эпоха
if epoch % 100 == 0 or epoch == epochs-1:
print(f'epoch: {epoch:5d} loss: {L:.4f} accuracy: {A:.4f}' )
В результате получим что-то типа:
before: loss: 0.6340 accuracy: 0.6950 epoch: 0 loss: 0.6327 accuracy: 0.6550 .... epoch: 999 loss: 0.0334 accuracy: 0.9908
Для улучшения обучения, обычно стоит перемешивать данные. Это можно сделать двумя способами. Первый запускается перед функцией fit в начале каждой эпохи:
idx = torch.randperm( len(X) ) # перемешанный список индексов
X = X[idx]
Y = Y[idx]
В этом методе создаётся новая память для всех данных, что для больших обучающих массив
не всегда хорошо. Второй способ делает случайную выборку только для текущего батча
внутри функции fit:
idx = torch.randint(high = len(X), size = (batch_size,) )
xb = X[idx]
yb = Y[idx]
Памяти при этом используется меньше, но при проходе по одной эпохе в обучение
могут попасть не все примеры, а в батч могут попасть одинаковые примеры.
Этот метод используется в классе DataLoader (параметр shuffle), см. ниже.
Таким образом, по сравнению с Keras в TensorFloor, процедуру обучения необходимо написать самостоятельно. Однако в сложных случаях это позволяет вмешиваться в процесс на любом этапе. Например, можно вставить свой оптимизатор :)
. if train: # в режиме обучения
L.backward() # вычисляем градиенты
with torch.no_grad():
for p in model.parameters():
p.add_(p.grad, alpha=-0.7) # p += -0.7*grad
p.grad.zero_()
Вывод структуры сети
Простейший способ увидеть слои сети, это просто вывести на печать модель:
print(model) # текстовое представление модели
Удобнее воспользоваться сторонним модулем modelsummary. В его функцию summary передаётся входной тензор с любыми значениями (но правильной формы) из одного примера (в shape это будет первая размерность -1):
from modelsummary import summary summary(model, torch.zeros(1, 2), show_input=False) # аналог summary в keras
-----------------------------------------------------------------------
Layer (type) Output Shape Param #
=======================================================================
Linear-1 [-1, 5] 15
Linear-2 [-1, 1] 6
=======================================================================
Total params: 21
Trainable params: 21
Non-trainable params: 0
Если установить show_input=True, то, вместо формы выхода,
будет печататься форма входа каждого слоя
Для составных моделей можно запускать функцию summary
с параметром show_hierarchical=True.
for layer in model:
print("***", layer)
for param in layer.parameters():
print(param.data.numpy())
В общем случае параметры модели выводятся таким образом:
for param in model.parameters():
print(param.numel(), param.size(), param.data.numpy())
tot = 0
for k, v in model.state_dict().items():
pars = np.prod(list(v.shape)); tot += pars
print(f'{k:20s} :{pars:7d} shape: {tuple(v.shape)} ')
print(f"{'total':20s} :{tot:7d}")
fc1.weight : 10 shape: (5, 2) fc1.bias : 5 shape: (5,) fc2.weight : 5 shape: (1, 5) fc2.bias : 1 shape: (1,) total : 21
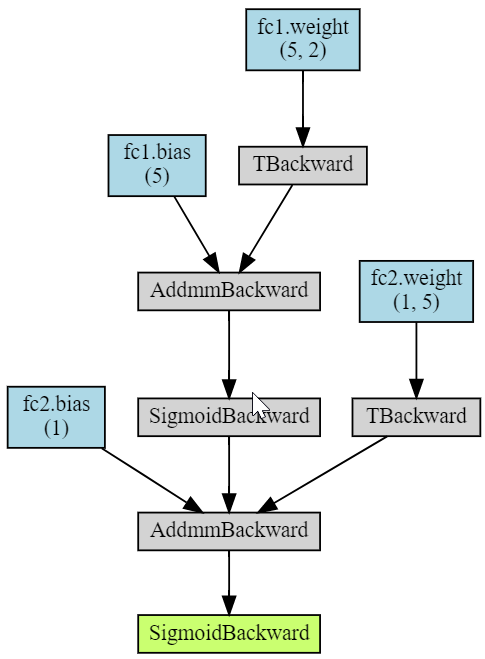
Наконец, библиотека torchviz позволяет изобразить вычислительный граф модели (рисунок справа):
import torchviz
torchviz.make_dot(model(X),
params = dict(model.named_parameters()) )
Узел AddmmBackward соответствует функции torch.addmm(v, m1, m2, b=1, a=1), которая перемножает матрицы и добавляет к ним вектор: b v + a (m1 @ m2).
Сохранение и загрузка
Метод torch.save сохраняет в бинарном виде любой словарь, в том числе состояния модели и оптимизатора:
import datetime
state = {'info': "Это моя сеть", # описание
'date': datetime.datetime.now(), # дата и время
'model' : model.state_dict(), # параметры модели
'optimizer': optimizer.state_dict()} # состояние оптимизатора
torch.save(state, 'state.pt') # сохраняем файл
Затем их можно загрузить, создав предварительно модель и оптимизатор (его парметры могут быть любыми,
т.к. они загрузятся из файла):
state = torch.load('state.pt') # загружаем файл
m = TwoLayersNet(2, 5, 1) # экземпляр сети
optimizer = torch.optim.SGD(m.parameters(),lr=1) # оптимизатор (любые параметры)
m. load_state_dict(state['model']) # получаем параметры модели
optimizer.load_state_dict(state['optimizer']) # получаем состояние оптимизатора
print(state['info'], state['date']) # вспомогательная информация
Классы датасетов
В PyTorch принято оборачивать обучающие данные в класс. Он является наследником класса Dataset и переопределяет метод __len__ числа примеров и метод __getitem__ получения примера по индексу idx:
class MyDataset(torch.utils.data.Dataset): # Наследник класса Dataset
def __init__(self, N = 10, *args, **kwargs):
super().__init__(*args,**kwargs)
self.x = torch.rand(N,1) # cлучайные данные
def __len__(self): # Количество примеров
return len(self.x)
def __getitem__(self, idx): # получить idx-тый пример
return {'input' : self.x[idx],
'target': 2*self.x[idx]}
data = MyDataset()
for sample in data:
print(sample) # {'input': tensor([0.1545]), 'target': tensor([0.3090])} ...
Создав датасет, его можно передать объекту DataLoader,
который будет выдавать батчи, перемешивать, разбивать на обучение и тест, нормализовать данные и т.п.
(см. документацию).
train_loader = torch.utils.data.DataLoader(dataset=data, batch_size=12, shuffle=False)
for batch in train_loader: # получаем батчи для тренировки
print(batch['input'], batch['target'])
Вычисления на GPU
Для вычисления на GPU (как и в общем случае) необходимо создать соответствующие вычислительные устройства:
gpu = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
cpu = torch.device("cpu")
После создания модели, её можно отправить на графическую карточку и (если позволяет её память)
тоже сделать с обучающими данными:
model = TwoLayersNet(2, 5, 1) # экземпляр сети model.to(gpu) # отправляем его на GPU X = X.to(gpu) # отправляем обучающие данные на GPU Y = Y.to(gpu)
Если для обучающих данных места на GPU не хватает, их можно отправлять туда батчами.
При обучении, ошибка пересылается из GPU в CPU. Заметим, что для маленьких моделей и обучающих массивов данных использование GPU не целесообразно и может даже замедлить обучение по сравнению с CPU.
Собственные слои
Слои, как и вся сеть, являются наследником класса nn.Module. Пример реализации линейного слоя:
import math
from torch.nn.parameter import Parameter
class My_Linear(nn.Module):
def __init__(self, in_F, out_F):
super(My_Linear, self).__init__()
self.weight = Parameter(torch.Tensor(out_F, in_F))
self.bias = Parameter(torch.Tensor(out_F))
self.reset_parameters()
def reset_parameters(self):
for p in self.parameters():
stdv = 1.0 / math.sqrt(p.shape[0])
p.data.uniform_(-stdv, stdv)
def forward(self, x):
return x @ self.weight.t() + self.bias
Собственный оптимизатор
Ниже приведен код простого SGD-оптимизатора. Обратим внимание на декоратор @torch.no_grad() перед методом step. Он означает, что этап изменения параметров будет выполняться при отключенном режиме построения графа.
class SGD(torch.optim.Optimizer):
def __init__(self, params, lr=0.1, momentum=0):
defaults = dict(lr=lr, momentum=momentum)
super(SGD, self).__init__(params, defaults)
@torch.no_grad()
def step(self):
for group in self.param_groups:
momentum = group['momentum']
lr = group['lr']
for p in group['params']:
if p.grad is None:
continue
grad = p.grad
if momentum != 0:
p_state = self.state[p]
if 'momentum_buf' not in p_state:
buf = p_state['momentum_buf'] = torch.clone(grad)
else:
buf = p_state['momentum_buf']
buf.mul_(momentum).add_( grad )
grad = buf
p.add_(grad, alpha = -lr)
optimizer = SGD(model.parameters(), lr=0.1, momentum=0.9)
Параметры готовых оптимизаторов можно также менять непосредственно в процессе обучения
def adjust_optim(optimizer, epoch):
if epoch == 1000:
optimizer.param_groups[0]['betas'] = (0.3, optimizer.param_groups[0]['betas'][1])
if epoch > 1000:
optimizer.param_groups[0]['lr'] *= 0.9999
