ML: Нейронные сети в Torch - Справочник

Интерфейсы для слоёв
Базовые слои:

Linear, Embedding, Conv2d, RNN, LSTM, MultiheadAttention, TransformerEncoderLayer, TransformerEncoder

Cлои без параметров:

Flatten, CosineSimilarity, PairwiseDistance, Dropout, BatchNorm1d, MaxPool2d, AvgPool2d

Активационные функции:
- Sigmoid, Tanh, ReLU, ELU, Softmax, LogSoftmax
Функции ошибки:
- MSELoss, BCELoss, CrossEntropyLoss, NLLLoss
Оптимизаторы

Интерфейсы для слоёв

Этот документ содержит обзор основных типов слоёв, ошибок и оптимизаторов в библиотеке PyTorch. Основы PyTorch описаны здесь, а основы программирования на ней нейронных сетей - здесь.

Слои в PyTorch реализованы в двух формах: как функции и как классы.

Первая - это обычные функции, которым передаются параметры слоя и входящий тензор. Например, линейный слой умножает входную матрицу формы (N, nX) на транспонированную матрицу весов W формы (nY, nX) и опционально добавляет вектор смещений bias. На выходе получается тензор (N, nY):

import  torch.nn.functional as F
 
N, nX, nY = 1, 2, 3                               # число примеров, входов, выходов
X = torch.ones(N,  nX)                            # матрица примеров
W = torch.ones(nY, nX)                            # матрица весов 
B = torch.ones(nY)                                # вектор смещений
 
Y = F.linear(X, W, B)                             # [[3., 3., 3.]]
Y = X.mm(W.t())+B                                 # тоже самое
Y = torch.addmm(B,X,W.t())                        # тоже самое

Слои как экземпляры классов, сами создают параметры с начальными случайными значениями.
Ниже обязательными аргументами при создании класса является число входов nX и число выходов nY слоя (число нейронов в нём == число новых признаков). Затем экземпляру fc класса Linear через оператор ( ) передаётся входная матрица X:

import torch.nn as nn
 
fc =  nn.Linear(nX, nY)
Y  = fc(X)                                        # tensor([[-0.1559, -0.2140, 0.1462]],
                                                  #         grad_fn=<Addmm>)

Класс слоя у своих параметров объявляет свойство requires_grad=True. Это приводит к построению вычислительного графа при прямом распространении по сети и к получению градиентов от параметров при обратном распространении:

print(fc.bias)            # tensor([ 0.529, -0.103,  0.646], requires_grad=True)
print(fc.bias.is_leaf)    # True
print(fc.bias.grad)       # None
 
L = torch.sum(Y*Y)        # скалярная "функция ошибки"
L.backward()              # запускаем вычисление градиентов
fc.bias.grad              # tensor([-0.3688,  0.6441, -1.6415])

Дальше идёт небольшой справочник наиболее важных типов слоёв, активационных функций и оптимизаторов. За более подробной информацией стоит обратиться к документации.

Базовые слои

Полносвязный слой

✒ nn.Linear
… (in_features, out_features, bias=True) [doc]

Осуществляет линейное преобразование $\mathbf{y} = \mathbf{x}\cdot \mathbf{W}^T + \mathbf{b}$ . Параметры слоя находятся в атрибутах weight и bias. Матрица весов $\mathbf{W}$ хранится в транспонированном виде (чтобы при перемножении матриц $\mathbf{X}\mathbf{W}^\top$ использовать их строки, а не строку и столбец). Если необходимо задать веса руками, это делается вне вычислительного графа:

fc = nn.Linear(nX, nY)
with torch.no_grad():
    fc.weight.copy_(W)     # устанавливаем матрицу весов
    fc.bias.  copy_(B)     # устанавливаем вектор смещений

Чтобы заморозить параметры (не менять при обучении) достаточно отключить у них вычисление градиента: fc.weight.requires_grad = False.

Реализация линейного слоя в torch.nn.functional выглядит следующим образом:

def linear(X, weight, bias=None):
    if X.dim() == 2 and bias is not None:       # fused op is marginally faster 
        ret = torch.addmm(bias, X, weight.t())  # bias + X @ weight.t()
    else:
        output = X.matmul(weight.t())
        if bias is not None: output += bias
        ret = output
    return ret

Пусть in_features=nX, out_features=nY и есть смещение: bias=True. Входной тензор может иметь произвольное число индексов (многоточие) и слой так меняет его форму: (N,...,nX) -> (N,...,nY).
Число параметров слоя равно nX*nY + nY.

Эмбеддинг

✒ nn.Embedding
… (num_embeddings, embedding_dim, padding_idx=None, max_norm=None, norm_type=2.0,
… scale_grad_by_freq=False, sparse=False, _weight=None)

Слой Embedding преобразует массив целых чисел long на входе в матрицу (массив векторов). Подробнее см. Embedding слов. При создании экземпляра слоя обязательны два первых параметра: размер словаря и размерность эмбеддига. Ниже создаётся слой с 5 словами и их 2-мерными (случайными) векторами:

emb = nn.Embedding(5, 2)
 
X = torch.tensor([0,2,1])
 
print (emb(X))
print(emb.weight)

tensor([[-1.3062, -1.6261],
        [-0.3903,  0.0998],
        [ 0.2643,  1.6466]],  grad_fn=<Embedding>)
Parameter containing:
tensor([[-1.3062, -1.6261],
        [ 0.2643,  1.6466],
        [-0.3903,  0.0998],
        [-0.5463, -0.5028],
        [ 1.3299, -0.0580]],  requires_grad=True)

При установлении параметра padding_idx=0, слово с нулевым индексом всегда будет имеет нулевые компоненты. Подобный паддинг используется в предложениях переменной длинны. Нулями забиваются "несуществующие слова" для выравнивания длин предложений.

Параметр max_norm задаёт максимальную длину векторов и если при обучении она превышается, вектор перенормируется. В качестве нормы по умолчанию используется сумма квадратов компонент: norm_type = 2.

При параметре scale_grad_by_freq = True градиенты при обучении будут взвешиваться по обратной частоте слов в батче (усиливать изменение более редких слов). Но батч при этом стоит брать достаточно большой. Загрузить готовые векторы можно, создав слой следующим образом:

weight = torch.FloatTensor([[1, 2.3, 3], 
                            [4, 5.1, 6]])
emb = nn.Embedding.from_pretrained(weight)    # Создать слой с готовыми векторами
input = torch.LongTensor([1])                 # Get embeddings for index 1
emb(input)                                    # tensor([[ 4.0,  5.1,  6.0]])

Параметры функции from_pretrained:

from_pretrained(embeddings, freeze=True, padding_idx=None, 
                max_norm=None, norm_type=2.0, scale_grad_by_freq=False, sparse=False)

Конволюция

✒ nn.Conv2d
… (in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True,
… padding_mode='zeros')

Свёрточный слой Conv2D применяется к "картинкам" высотой rows, шириной cols и имеющих in_channels "цветовых" каналов. На самом деле графические термины условны и слой Conv2D может применяться не только при обработке изображений. Форма входного тензора (N, in_channels, rows, cols). На выходе будет тензор (N, out_channels, rows_out, cols_out) По исходному тензору проходит out_channels фильтров размером kernel_size (число или tuple). Глубина фильтра определяется числом входных каналов in_channels.

Ниже на рисунке in_channels=2, out_channels=3 (три фильтра), размеры фильтров kernel_size = 2 или, что тоже kernel_size = (2,2). Фильтры по умолчанию скользят по картинке с шагом один stride=(1,1), поэтому результирующие ширина и высота картинки на 1 меньше:

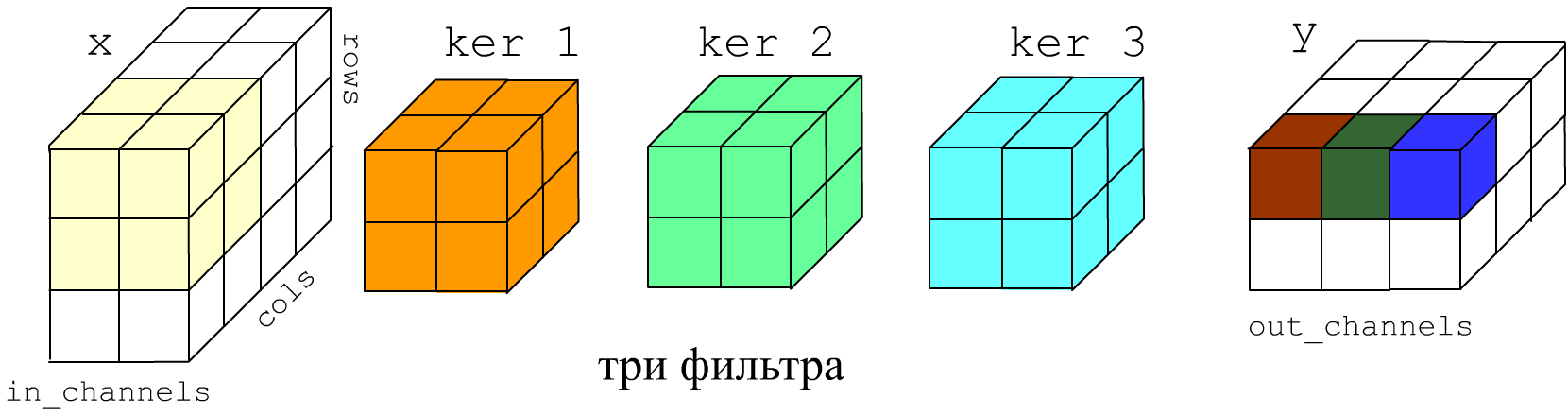
Параметр padding (int or tuple) задаёт на сколько "пикселей" необходимо расширить картинку с обоих сторон, перед прохождением по ней фильтрами. Расширенная область заполняется значениями в соответствии с параметром padding_mode: 'zeros', 'reflect', 'replicate', 'circular'. Параметр dilation = 1 задаёт расстояние между пикселями, попадающими в фильтр.

Для примера создадим "картинку" 3x4, левая половина которой белая (1), а правая - чёрная (0) и пройдём по ней фильтром 2x2, выделяющим вертикальный край:

X = torch.zeros(1,1,3,4)
X[0,0,:,:2] = 1
print(X)
 
conv = nn.Conv2d(1,1,kernel_size=2,bias=False)
print( conv ) 
 
with torch.no_grad():
    conv.weight.copy_(torch.tensor([[-1.,1.], 
                                    [-1.,1.]]))
 
print( conv.weight )
print( conv.bias )
print( conv(X) )

tensor([[[[1., 1., 0., 0.],
          [1., 1., 0., 0.],
          [1., 1., 0., 0.]]]])
           
Conv2d(1,1,kernel_size=(2,2),stride=(1,1))
 
 
# задаём ядро фильтра
tensor([[[[-1.,1.],
          [-1.,1.]]]],requires_grad=True)
None
tensor([[[[ 0., -2.,  0.],
          [ 0., -2.,  0.]]]], 
          grad_fn=<ThnnConv2D>)

RNN

✒ nn.RNN
… (input_size, hidden_size, num_layers=1, nonlinearity='tanh', bias=True,
… batch_first=False, dropout=0, bidirectional=False) [doc]

Базовый рекуррентный слой по входу $\mathbf{x}^{(t)}$ и предыдущему скрытому состоянию $\mathbf{h}^{(t-1)}$ вычисляется новое скрытое состояние $\mathbf{h}^{(t)}$ : $\mathbf{h}^{(t)} = \tanh(\mathbf{x}^{(t)}\,\mathbf{W}_{ih} + \mathbf{b}_{ih} + \mathbf{h}^{(t-1)}\,\mathbf{W}_{hh} + \mathbf{b}_{hh})$

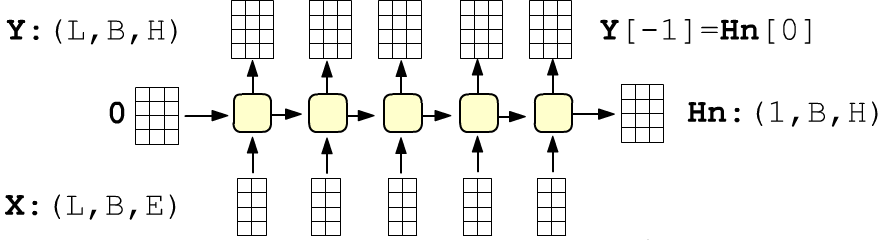
Обязательные параметры: input_size - размерность входов ( $\mathbf{x}$ ) и hidden_size - размерность выхода ( = скрытого состояния $\mathbf{h}$ ).

По умолчанию размерность входа (seq_len, batch_size, input_size), где seq_len - число RNN-ячеек (входов). Индекс батча можно сделать первым при помощи параметра batch_first. Впрочем тензор по умолчанию получается, если перед слоем RNN находится слой Embedding c seq_len входами и с input_size = VEC_DIM размерностью векторов.

Слой возвращает кортеж из тензора всех выходов сети формы (seq_len, batch_size, hidden_size) и последнего скрытого состояния (последний выход) формы (num_layers, batch_size, hidden_size), где для одного слоя num_layers = 1. По умолчанию компоненты начального скрытого состояние нулевые. Иначе их можно передать вторым аргументом:

X_dim  = 2           # размерность входов             = dim(x)
H_dim  = 4           # размерность скрытого состояния = dim(h)
L      = 3           # число входов (ячеек RNN слоя)
B      = 1           # число примеров (batch_size)
 
rnn = nn.RNN(X_dim, H_dim)
 
X  = torch.zeros(L, B, X_dim)
H0 = torch.zeros(1, B, H_dim)     
 
Y, Hn = rnn(X, H0)                       # H0 не обязательно, по умолчанию и так 0
 
print(tuple(Y.shape), tuple(Hn.shape))   #  (3, 1, 4) (1, 1, 4)
print(Y[-1] == Hn[-1])                   #  tensor([[[True, True, True, True]]])

В слое можно сразу задать стопку RNN-слоёв (num_layers) Между слоями можно вставить режим случайного забивания нулями выходов с вероятностью dropout. Слой можно также превратить в двунаправленный: bidirectional = True. В этом случае размерность выхода будет (inputs, batch_size, 2*hidden_size), а размерность начального скрытого состояния (2 * num_layers, batch_size, hidden_size).

LSTM

✒ torch.nn.LSTM
… (input_size, hidden_size, num_layers=1, nonlinearity='tanh', bias=True,
… batch_first=False, dropout=0, bidirectional=False) [doc]

Аналогичен RNN. Подробности см. в NN_RNN.html. Кроме скрытого состояния $\mathbf{h}$ имеет память ячеек $\mathbf{c}$ , см. документацию.

rnn = nn.LSTM(10, 20, 2)
...
output, (hn, cn) = rnn(input, (h0, c0))

MultiheadAttention

✒ nn.MultiheadAttention
… (embed_dim, num_heads, dropout=0.0, bias=True, add_bias_kv=False,
… add_zero_attn=False, kdim=None, vdim=None)

$\text{MultiHead}(\mathbf{Q},\mathbf{K}, \mathbf{V}) = \text{Concat}(\text{h}_1,\dots,\text{h}_H)\,\mathbf{W}^O, ~~~~~~~ \text{h}_i = \text{Attn}(\mathbf{Q}\,\mathbf{W}_i^Q,~ \mathbf{K}\,\mathbf{W}_i^K,~ \mathbf{V}\,\mathbf{W}_i^V)$

Inputs: Q:(L,N,E), K,V:(S,N,E), где L - длина последовательности target (для декодера),
N - размер батча, E - размерность эмбединга (embed_dim), S - длина последовательности source.

Outputs: output: (L,N,E), weights: (N,L,S)

Размерности матриц: $\mathbf{W}^Q:$ (E, E), $\mathbf{W}^K:$ (E, kdim), $\mathbf{W}^V:$ (E, vdim), где kdim,vdim задаются или равны E, но они передаются в функцию linear, поэтому при умножении транспонируются.
Размерность каждой головы равны head_dim = E // num_heads.
Выходная матрица $\mathbf{W}^O:$ это слой Linear(E, E, bias=bias).
Если bias есть, он добавляется после умножения на проекционные матрицы $\mathbf{W}^Q,\mathbf{W}^K,\mathbf{W}^V$ (к каждой свой).

Если эмбединг входов одинаковый, то проекционные матрицы упакованы в in_proj_weight формы (3*E,E), иначе это параметры: q_proj_weight, k_proj_weight, v_proj_weight. Смещение (если он есть) это in_proj_bias формы (3*E,), а выходной слой: out_proj.

Концептуально происходят следующие вычисления (N - размер батча, подробности см. в NN_Attention.html):

q = linear(Q, q_proj_weight, in_proj_bias[0 : E])     # (L,N,E) @ (E, E).T    = (L,N,E)
k = linear(K, k_proj_weight, in_proj_bias[E : E*2])   # (S,N,E) @ (E, kdim).T = (S,N,kdim)
v = linear(V, v_proj_weight, in_proj_bias[E*2:])      # (S,N,E) @ (E, vdim).T = (S,N,vdim)
 
q = q.contiguous().view( L, N * num_heads, head_dim).transpose(0,1)
k = k.contiguous().view(-1, N * num_heads, head_dim).transpose(0,1)
v = v.contiguous().view(-1, N * num_heads, head_dim).transpose(0,1)
 
a_weights = torch.bmm(q, k.transpose(1,2))
a_weights = softmax(a_weights, dim=-1)
 
a = torch.bmm(a_weights, v)
 
a = a.transpose(0, 1).contiguous().view(L, N, E)
a = linear(a, out_proj_weight, out_proj_bias)

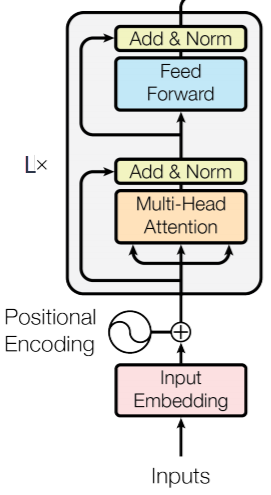
TransformerEncoderLayer

✒ nn.TransformerEncoderLayer
… (d_model, nhead, dim_feedforward=2048, dropout=0.1, activation='relu')

Параметры: d_model – размерность входа (вектора одного токена), nhead – число голов (делитель параметра d_model), dim_feedforward – размерность полносвязной сети.

TransformerEncoder

✒ nn.TransformerEncoder
… (encoder_layer, num_layers, norm=None)

L, N, E = 10, 32, 512            # число слов, размер батча, размерность эмбединга
 
encoder_layer       = nn.TransformerEncoderLayer(d_model=E, nhead=8)
transformer_encoder = nn.TransformerEncoder     (encoder_layer, num_layers=6)
 
src = torch.rand(L, N, E)
out = transformer_encoder(src)   # out.shape == src.shape

Cлои без параметров

Лиаринизация тензора

✒ nn.Flatten(start_dim=1, end_dim=-1)

При создании с параметрами по умолчанию, все индексы кроме первого (индекс примера) сольются в один (для каждого примера получится вектор). Слой параметров не имеет.

X = torch.ones(2, 5,4,3)
Y = torch.nn.Flatten()(X)
print( tuple(Y.shape) )                   # (2, 60)

Косинус между векторами

✒ nn.CosineSimilarity(dim=1, eps=1e-08)

$\frac{\mathbf{u}\mathbf{v}}{ \max( |\mathbf{u}|\,|\mathbf{v}|,~~\epsilon) }$

Input1, Input2: (*, D, *), где D - размерность вектора и формы одинаковые. Output: (*,*).
Ниже косинус вычисляется между строчками матриц:

u, v = torch.randn(100, 128), torch.randn(100, 128)
output = nn.CosineSimilarity(dim=1, eps=1e-6) (u, v)

Расстояние между векторами

✒ nn.PairwiseDistance(p=2.0, eps=1e-06, keepdim=False)

$\bigr(\sum_{i} |x_i|^p \Bigr)^{1/p}$

Input1, Input2: (N, D), где D - размерность вектора. Output: (N) или (N, 1), если keepdim = True.

Отключение нейронов

✒ nn.Dropout(p=0.5, inplace=False)

В режиме тренировке: m.train(), с вероятностью "p" зануляет каждый элемент матрицы и делит их на 1-p.
В режиме оценивания: m.eval() ничего не делает. Благодаря делению на 1-p среднее значение по модулю элементов в режиме тренировки будет такой-же, как и врежиме оценивания (у входного тензора).

m = nn.Dropout(p = 0.2)
                               #                     v                      v
print( m(torch.ones(10)) )     # [1.25, 1.25, 1.25, 0.0, 1.25, 1.25, 1.25, 0.0, 1.25, 1.25]
 
x = torch.randn(100, 100)
 
m.eval()                       # This is equivalent with self.train(False)
y = m(x)
print( (x==y).float().mean() ) # не меняется
 
m.train() 
y =m(x)
 
print(x.abs().mean(),   (x*x < 1e-10).float().mean()  )   # 0.8025     0.
print(y.abs().mean(),   (y*y < 1e-10).float().mean()  )   # 0.8001     0.206

Нормализация тензора

✒ nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)

По батчу (перый индекс) вычисляются средние значения и дисперсии по каждому признаку независимо. Затем делается нормализаци данных и афинный сдвиг с обучаемыми параметрами $\gamma,\,\beta$ . $y = \frac{x - \mathrm{E}[x]}{\sqrt{\mathrm{Var}[x] + \epsilon}} \odot \text{weight} + \text{bias}$ Вход должен быть тензором формы (N,F) или (N,F,L). Параметр num_features = F. Для тензора (N,F,L) усреднение происходит для dim=0,2, т.е. одинаковые средние по каждому "входу" последнего индекса [0...L-1].

В процессе тренировки средние значения сглаживаются скользящим средним с параметром momentum (если None - то обычное среднее). Эти средние запоминаются и затем используются при тестировании (даже с одним батчем).

m =  nn.BatchNorm1d(2)
 
x = torch.randn(100000,2)
print( x.mean(dim=0), x.var(dim=0) )    # [-0.0005,  0.0067]      [1.0058, 0.9956]
 
x = 2 *  x + 3
print( x.mean(dim=0), x.var(dim=0) )    # [ 3.0010,  2.9867]      [4.0231, 3.9824]
 
y = m(x)
with torch.no_grad():
    print(y.mean(dim=0), y.var(dim=0))  # [ 0.0000,  0.0000]      [1.0000, 1.0000]
     
     
for k, v in m.state_dict().items():     # weight             :(2,)
    print(f'{k:20s}: {tuple(v.shape)}') # bias               :(2,)
                                        # running_mean       :(2,)
                                        # running_var        :(2,)
                                        # num_batches_tracked:(  )

MaxPool2d

✒ nn.MaxPool2d
(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)

AvgPool2d

✒ nn.AvgPool2d
(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True, divisor_override=None)

Активационные функции

Сигмоид:

$\mathrm{Sigmoid}(x) = 1/(1+e^{-x})$

✒ nn.Sigmoid() [doc]
✒ F.sigmoid(x)

Tanh:

$\mathrm{Tanh}(x) = (e^{x}-e^{-x})/(e^{x}+e^{-x})$

✒ nn.Tanh() [doc]
✒ F.tanh(x)

ReLU:

$\mathrm{Sigmoid}(x) = \max(0,x)$

✒ nn.ReLU(inplace=False) [doc]
✒ F.relu(x, inplace=False)

ELU:

$\mathrm{ELU}(x) = \max(0,x) + \min(0, \alpha\,(e^{x}-1))$

✒ nn.ELU(alpha=1.0, inplace=False) [doc]
✒ nn.elu(x, alpha=1.0, inplace=False)

Софтмакс:

$\mathrm{Softmax}(x_i) = e^{x_i}/\sum_j e^{x_j}$

✒ nn.Softmax(dim=None) [doc].
✒ F.softmax(x, dim)

X = torch.tensor( [ [1.,2.,3] ] )
torch.nn.Softmax(dim=1)(X)              # tensor([[0.09, 0.24, 0.66]])

Логарифмический софтмакс:

$\mathrm{LogSoftmax}(x_i) = \log \bigr(e^{x_i}/\sum_j e^{x_j}\bigr)$

✒ nn.LogSoftmax (dim=None) [doc].

Функции ошибки

Среднеквадратичная ошибка

✒ nn.MSELoss
… (size_average=None, reduce=None, reduction='mean') [doc] $L(y,\hat{y}) = (y - \hat{y})^2 \left\{ \begin{array}{ll} .\mathrm{mean}() & \text{if reduction='mean'}\\ .\mathrm{sum}() & \text{if reduction='sum'} \end{array} \right.$

По умолчанию (reduction='mean') квадраты отклонений усредняются по всем примерам батча и по всем выходам (ошибка это скаляр!).

loss = torch.nn.MSELoss()
 
y  = torch.rand(10, 2)                  # 10 примеров, 2 выхода
yb = torch.rand(10, 2)
 
loss(y, yb) == ((y-yb)**2).mean()  

Бинарная кросс-энтропия

✒ nn.BCELoss
… (weight=None, size_average=None, reduce=None, reduction='mean') [doc]

Предполагается, что эта ошибка ставится после сигмоидной активации, т.е. выходы модели y и целевые значения yb находятся в диапазоне [0...1]. Обычно BCELoss используется для сети с одним выходом (задача для двух классов 0 и 1). Если классы пересекаются (т.е. пример может относится сразу к нескольким классам), то число выходов равно числу классов. По умолчанию (reduction='mean') ошибки усредняются по всем примерам и всем выходам:

loss = torch.nn.BCELoss()
 
y  = torch.rand(10, 2, 3)                  # 10 примеров, 2x3 выходов
yb = torch.rand(10, 2, 3)
 
print(    loss(y, yb) )
print(  -( yb*y.log() + (1-yb)*(1-y).log() ).mean()  )

Вектор weight с числом компонент равных числу примеров в батче может по-разному взвешивать различные примеры. Ошибка для

$i$ -го примера (

$y$ - выход модели,

$\hat{y}$ - целевое значение):

$L_i = -w_i\,\bigr[ \hat{y}_i\,\log y_i + (1-\hat{y}_i)\,\log (1-y_i)\bigr]$

Кросс-энтропия

✒ nn.CrossEntropyLoss
… (weight=None,size_average=None,ignore_index=-100,reduce=None,reduction='mean') [doc]

Применяется к задаче классификации не пересекающихся $C$ классов. Сеть должна иметь $C$ выходов, т.е. в ошибку из модели входит тензор $y_{i\alpha}$ формы $(N,C)$ , где $N$ - размер батча. Целевыми являются целые числа $\hat{y}_i \in [0...C-1]$ - номера классов каждого примера формы (N,). Ошибка для одного $i$ -того примера и $\hat{y}_i=c$ равна:

$L(y, c) = -\,w_c\,\log\left( \frac{\exp {y_{ic}}}{ \sum_\alpha \exp{y_{i\alpha}}}\right).$ Веса

$w_\alpha$ (по числу классов) могут усиливать вклад отдельных классов. Таким образом, CrossEntropyLoss совмещает в себе Softmax и на выходе сети его ставить не нужно.

$C$ выходов сети

$y_{i\alpha}$ превращаются в "вероятности" и максимизируется логарифм вероятности правильного класса

$\hat{y}_i=c$ (знак минус - ошибка минимальна). Итоговая ошибка равна среднему

$L(y, c)$ по всем примерам батча (если reduction='mean').

Входные данные в функцию ошибки CE_loss(y, y_t)могут иметь форму y=(B,C):float, y_t=(B,):long или в n-мерном случае: y=(B,C,L1,...,Ln):float, y_t=(B,L1,...,Ln):long

B, C, L = 10, 5, 4                   # примеров, классов, выходов
w = torch.rand(C)                    # веса важности классов
 
CE_loss = nn.CrossEntropyLoss(weight=w, ignore_index=1)   
 
y     = torch.randn(B, C, L)
yb    = torch.empty(B, L,     dtype=torch.long).random_(C)
 
loss  = CE_loss(y, yb)
print(loss)                          # ошибка

Воспроизведём, полученное значение:

y = -nn.Softmax(dim=1)(y).log()      # минус логарифма от софтмакса 
 
loss, norm = 0, 0
for b in range(B):
    for l in range(L):
        c = yb[b,l]                  # правильный класс
        if c != 1:                   # игнорируем класс 1
            loss += w[c]*y[b, c, l]  # ошибка
            norm += w[c]             # нормировка
print(loss/norm)

Логарифмический максимум правдоподобности

✒ nn.NLLLoss
… (weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean') [doc]

Результат будет таким же как и при CrossEntropyLoss, если последним слоем стоит LogSoftmax.

Оптимизаторы

torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), 
                 eps=1e-08, weight_decay=0, amsgrad=False)

torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, 
                    initial_accumulator_value=0, eps=1e-10)

torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)

torch.optim.RMSprop(params, lr=0.01, alpha=0.99, weight_decay=0, momentum=0,
                    eps=1e-08, centered=False)

torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))

torch.optim.SGD(params, lr, momentum=0, 
                dampening=0, weight_decay=0, nesterov=False)