ML: Рекуррентные сети на PyTorch
Введение
Иногда обучающие данные представляют собой набор упорядоченных последовательностей. Примерами являются временные ряды (котировки акций, показания сенсоров) или текст на естественном языке. В этих случаях подходящей архитектурой являются рекуррентные нейронные сети RNN (recurrent neural network).
Мы будем использовать фреймфорк PyTorch с основами которого можно познакомиться здесь и здесь. Импорт его библиотек выглядит следующим образом:
import torch import torch.nn as nnВсе примеры находятся в файле ML_RNN_Torch.ipynb, а обсуждение рекуррентных сетей на библиотеке Keras приведено здесь.
Простая RNN
Рекуррентный слой состоит из L ячеек с одинаковыми параметрами.
На его вход подают упорядоченную последовательность $\mathbf{x}^{(0)},...,\mathbf{x}^{(\mathrm{L}-1)}$ длины L.
Элементы последовательности - это E-мерные векторы признаков
$\mathbf{x}^{(t)}=\{x^{(t)}_0,...,x^{(t)}_{\mathrm{E}-1}\}$
(E от эмбединга слов).
Первый вектор поступает на вход первой ячейки, второй - на вход второй и т.д.
Каждая ячейка характеризуется H-мерным вектором скрытого состояния
$\mathbf{h}=\{h_0,...,h_{\mathrm{H}-1}\}$.
Этот вектор является выходом ячейки (стрелка вверх),
и он же отправляется в следующую ячейку. Внутри простой RNN-ячейки
проводится следующее вычисление (для $t=0,...,\text{L}-1$):
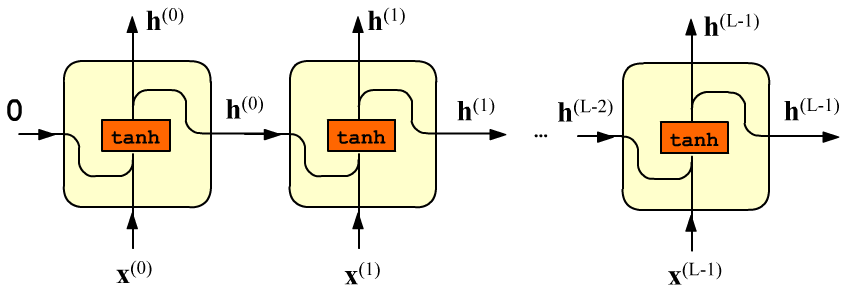
Матрицы $\mathbf{W}:$(E, H), $~\mathbf{H}:$(H, H) и вектор $~\mathbf{b}:$(H,) являются параметрами ячейки (и всего слоя). Так как ячейки одинаковые, число входов L на число параметров не влияет. Общее число параметров равно (E + H + 1) * H. Начальный вектор скрытого состояния $\mathbf{h}^{(-1)}$ (входящий в первую ячейку) или равен нулю $\mathbf{0}$ или задаётся руками.
Нелинейная функция гиперболического тангенса $\tanh(x)=(e^x-e^{-x})/(e^x+e^{-x})$ , как обычно, необходима, чтобы последовательность матричных умножений не "схлопнулась" в одно. Знакопеременность tanh борется с неконтролированным положительным ростом компонент вектора $\mathbf{h}^{(t)}$ при последовательном (рекуррентном) умножении матриц.
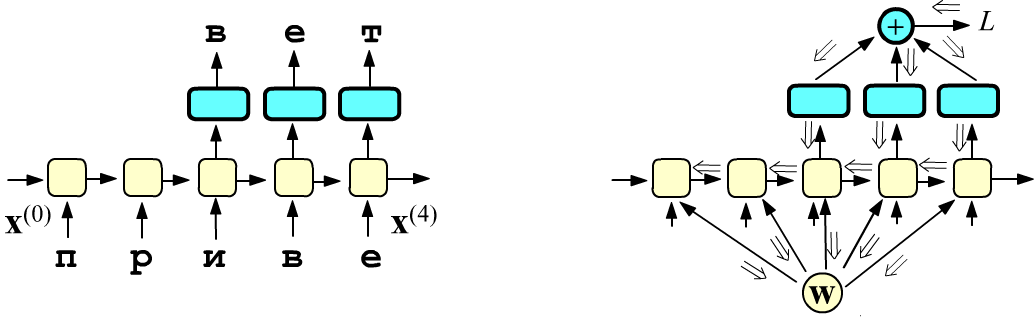
Примеры RNN-архитектур
 Вектор скрытого состояния постепенно "накапливает" усреднённую информацию о предыдущих входах.
Финальный вектор $\mathbf{h}^{(\mathrm{L}-1)}$ характеризует всю последовательность и называется
контекстным вектором (context vector).
Его можно, например, направить в стопку линейных слоёв,
на выходе которых происходит классификация текста (sentiment analysis - положительный или отрицательный отзыв на продукт)
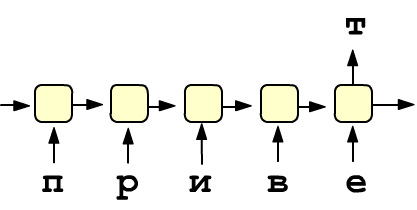
или предсказание очередного члена последовательности. Справа приведен пример простой архитектуры,
предсказывающей следующую букву в тексте. При этом предполагается наличие дополнительных слоёв.
Вектор скрытого состояния постепенно "накапливает" усреднённую информацию о предыдущих входах.
Финальный вектор $\mathbf{h}^{(\mathrm{L}-1)}$ характеризует всю последовательность и называется
контекстным вектором (context vector).
Его можно, например, направить в стопку линейных слоёв,
на выходе которых происходит классификация текста (sentiment analysis - положительный или отрицательный отзыв на продукт)
или предсказание очередного члена последовательности. Справа приведен пример простой архитектуры,
предсказывающей следующую букву в тексте. При этом предполагается наличие дополнительных слоёв.
 Номер буквы в алфавите подаётся на вход слоя векторизации Embedding.
На его выходе получается E-мерный вектор, компоненты которого являются параметрами обучения.
После прохождения через RNN-ячейку это вектор меняет свою размерность,
превращаясь в H-мерный вектор новых признаков на выходе ячейки.
Затем он отправляется в обычный полносвязый слой (fully connected) с "C" нейронами,
где "C" равно числу букв в алфавите.
Прохождение этого C-мерного вектора через softmax-функцию
даёт "вероятности" очередной буквы в последовательности. Задача обучения состоит в подборе параметров
RNN-ячейки и векторов эмбединга таким образом, чтобы вероятность предсказания
правильной буквы была максимальной.
Номер буквы в алфавите подаётся на вход слоя векторизации Embedding.
На его выходе получается E-мерный вектор, компоненты которого являются параметрами обучения.
После прохождения через RNN-ячейку это вектор меняет свою размерность,
превращаясь в H-мерный вектор новых признаков на выходе ячейки.
Затем он отправляется в обычный полносвязый слой (fully connected) с "C" нейронами,
где "C" равно числу букв в алфавите.
Прохождение этого C-мерного вектора через softmax-функцию
даёт "вероятности" очередной буквы в последовательности. Задача обучения состоит в подборе параметров
RNN-ячейки и векторов эмбединга таким образом, чтобы вероятность предсказания
правильной буквы была максимальной.
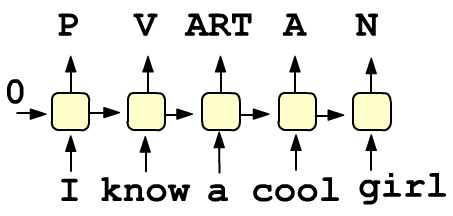 Можно использовать не только последнее скрытое состояние, но и скрытые состояния всех ячеек.
Например, архитектура сети, осуществляющая разметку текста, при которой каждому слову ставится в соответствие его часть речи (местоимение,
глагол, артикль, прилагательное, существительное) имеет вид, приведенный справа.
Как и в предыдущем примере, на всех входах должны быть слои эмбединга слов.
На выходе - полносвязный свой с числом нейронов, равному числу частей речи и софтмакс-функция дающая их вероятности.
Можно использовать не только последнее скрытое состояние, но и скрытые состояния всех ячеек.
Например, архитектура сети, осуществляющая разметку текста, при которой каждому слову ставится в соответствие его часть речи (местоимение,
глагол, артикль, прилагательное, существительное) имеет вид, приведенный справа.
Как и в предыдущем примере, на всех входах должны быть слои эмбединга слов.
На выходе - полносвязный свой с числом нейронов, равному числу частей речи и софтмакс-функция дающая их вероятности.
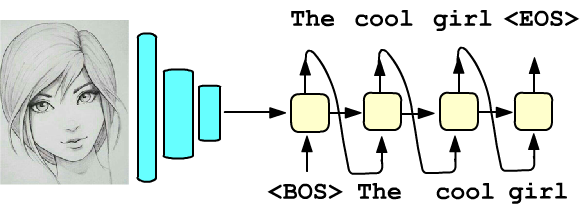 В примерах выше начальное скрытое состояние, поступающее на первую ячейку,
являлось нулевым вектором.
В качестве этого вектора, можно также использовать призводные признаки некоторого
объекта. Например, справа схемативно представлена задача текстового описания изображения.
Пиксели исходной картинки пропускаются через последовательность свёрточных слоёв. Веса этих слоёв обучаются
на некоторой другой задаче (например, распознавания классов объектов). Финальный слой свёрточной сети
в виде начального скрытого состояния направляется в RNN-слой.
Входом его первой ячейки является эмбединг служебного токена (слова) <BOS> (begin of sentence).
Рекуррентную сеть учат на выходах выдавать релевантный картинке текст. При этом первое сгенерённое слово поступает на вход второй
ячейки и т.д., пока на некоторой итерации слой не выдаст служебный токен <EOS> (end of sentence).
В примерах выше начальное скрытое состояние, поступающее на первую ячейку,
являлось нулевым вектором.
В качестве этого вектора, можно также использовать призводные признаки некоторого
объекта. Например, справа схемативно представлена задача текстового описания изображения.
Пиксели исходной картинки пропускаются через последовательность свёрточных слоёв. Веса этих слоёв обучаются
на некоторой другой задаче (например, распознавания классов объектов). Финальный слой свёрточной сети
в виде начального скрытого состояния направляется в RNN-слой.
Входом его первой ячейки является эмбединг служебного токена (слова) <BOS> (begin of sentence).
Рекуррентную сеть учат на выходах выдавать релевантный картинке текст. При этом первое сгенерённое слово поступает на вход второй
ячейки и т.д., пока на некоторой итерации слой не выдаст служебный токен <EOS> (end of sentence).
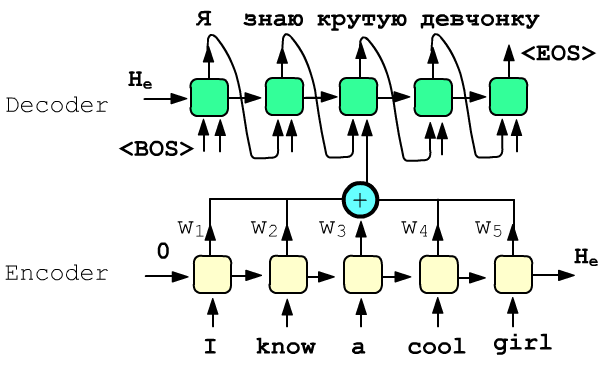 Последний пример связан с машинным переводом и архитектурой внимания (attention).
Пусть есть два рекуррентных слоя с различными параметрами.
Первый называется энкодер (encoder), а второй - декодер (decoder).
На входы ячеек энкодера поступают эмбединги слов предложения
"I know a cool girl"
на исходном (source) языке.
На выходах декодера ожидается перевод предложения на целевом (target) языке:
"Я знаю крутую девчонку".
Последний пример связан с машинным переводом и архитектурой внимания (attention).
Пусть есть два рекуррентных слоя с различными параметрами.
Первый называется энкодер (encoder), а второй - декодер (decoder).
На входы ячеек энкодера поступают эмбединги слов предложения
"I know a cool girl"
на исходном (source) языке.
На выходах декодера ожидается перевод предложения на целевом (target) языке:
"Я знаю крутую девчонку".
Скрытые состояния RNN-энкодера, как обычно, накапливают информацию об исходном предложении. Их сумма с некоторыми весами $w_i$ поступает в качестве дополнительных входов на ячейки рекуррентного слоя декодера (на рисунке показан только один такой вход). Веса вычисляются обучаемой функцией от скрытых состояний энкодера и скрытого состояния декодера из предшествующей ячейки (в примере это "знаю"). Текущее скрытое состояние декодера "предполагает", что в исходном предложении важно для перевода и "фокусирует внимание" на нужной информации, что отражается в значении весов $w_i$.
Матричные умножения
Рассмотрим как перемножаются матрицы $\mathbf{x}^{(t)}\cdot \mathbf{W} + \mathbf{h}^{(t-1)}\cdot \mathbf{H} + \mathbf{b}$
при вычислении скрытого состояния.
В общем случае в RNN-ячейку текущий вход $\mathbf{x}^{(t)}$ поступает пачками (batches) по
B штук в каждой пачке.
Поэтому $t$-тый вектор признаков $\mathbf{x}^{(t)}$ является матрицей формы (B,E)
(в строчках находятся примеры).
Эта матрица умножается на матрицу $\mathbf{W}:$ (E,H) слева
и затем добавляется произведение матриц $\mathbf{h}^{(t-1)}:$ (B,H)
и $\mathbf{H}:$ (H,H). К результате добавляется вектор смещения $\mathbf{b}$:
$$
\underbrace{\text{(B,E)} \cdot \text{(E,H)}}_{\mathbf{x}^{(t)}\,\cdot\,\mathbf{W}} ~~~+~~~
\underbrace{\text{(B,H)}\cdot\text{(H,H)}}_{\mathbf{h}^{(t-1)}\,\cdot\,\mathbf{H}} ~~~+~~~
\underbrace{\text{(1,H)}}_{\mathbf{b}} ~~~=~~~ \text{(B,H)}
$$
Пусть размерности входа и скрытого состояния равны E=2 и H=3,
а примеров в пачке B=4. Тогда в одной ячейке происходит следующее вычисление,
результат которого затем пропускается через tanh:
Тоже самое получится компактнее, если сделать конкатенацию векторов $\mathbf{x}^{(t)}$, $\mathbf{h}^{(t-1)}$ справа: torch.cat([x,h], dim=1) и присоеденить матрицу $\mathbf{H}$ к матрице $\mathbf{W}$ снизу: torch.cat([W,H], dim=0):
$$ \begin{array}{|c|c|c|c|c|} \hline x^{(t)\phantom{-1}}_{00} & x^{(t)\phantom{-1}}_{01} & h^{(t-1)}_{00} & h^{(t-1)}_{01}& h^{(t-1)}_{02}\\ \hline x^{(t)\phantom{-1}}_{10} & x^{(t)\phantom{-1}}_{11} & h^{(t-1)}_{10} & h^{(t-1)}_{11}& h^{(t-1)}_{12}\\ \hline x^{(t)\phantom{-1}}_{20} & x^{(t)\phantom{-1}}_{21} & h^{(t-1)}_{20} & h^{(t-1)}_{21}& h^{(t-1)}_{22}\\ \hline x^{(t)\phantom{-1}}_{30} & x^{(t)\phantom{-1}}_{31} & h^{(t-1)}_{30} & h^{(t-1)}_{31}& h^{(t-1)}_{32}\\ \hline \end{array} \cdot \begin{array}{|c|c|c|} \hline W_{00}^{\phantom{(0)}} & W_{01} & W_{02} \\ \hline W_{10}^{\phantom{(0)}} & W_{11} & W_{12} \\ \hline H_{00}^{\phantom{(0)}} & H_{01} & H_{02} \\ \hline H_{10}^{\phantom{(0)}} & H_{11} & H_{12} \\ \hline H_{20}^{\phantom{(0)}} & H_{21}& H_{22} \\ \hline \end{array} ~~+~~ \begin{array}{|c|c|c|} \hline b_{0} & b_{1} & b_{2}\\ \hline \end{array} ~~=~~ \begin{array}{|c|c|c|} \hline r_{00} & r_{01} & r_{02}\\ \hline r_{10} & r_{11} & r_{12}\\ \hline r_{20} & r_{21} & r_{22}\\ \hline r_{30} & r_{31} & r_{32}\\ \hline \hline \end{array} $$
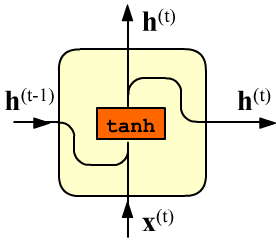 Именно поэтому в ячейке рисуются слитые в одну стрелки векторов $\mathbf{x}^{(t)},\mathbf{h}^{(t-1)}$
на входе $\tanh$.
Именно поэтому в ячейке рисуются слитые в одну стрелки векторов $\mathbf{x}^{(t)},\mathbf{h}^{(t-1)}$
на входе $\tanh$.
Такие вычисления проводятся в каждой ячейке. Если входной тензор X
имеет форму (L,B,E),
то X[t] являются матрицами (B,E), рассмотренными выше:
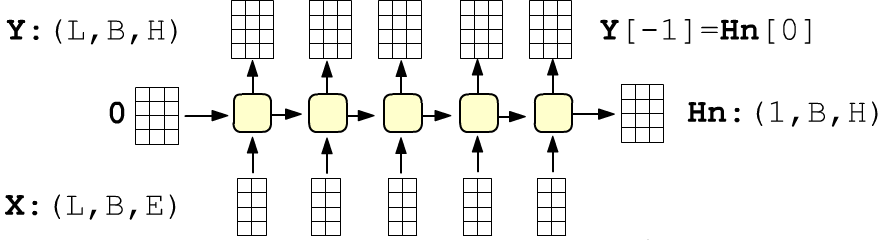
Формой скрытого состояния последней ячейки Hn для единообразия принято считать (1,B,H), а не (B,H).
Рекуррентные сети в PyTorch
В PyTorch простой рекуррентный слой называется nn.RNN. Его обязательными параметрами являются размерность входов E и скрытых состояний H:
E, H = 2, 3 # размерности входов и скрытых состояний B, L = 4, 5 # число примеров, длина примера (число векторов) rnn = nn.RNN(E, H) # экземпляр класса nn.RNNВыведем имена параметров RNN-слоя и их формы:
for k, v in rnn.state_dict().items(): # weight_ih_l0 : (3, 2) (H,E)
print(f'{k:10s} : {tuple(v.shape)}') # weight_hh_l0 : (3, 3) (H,H)
# bias_ih_l0 : (3,) (H,)
# bias_hh_l0 : (3,) (H,)
Как и в линейном слое, матрицы весов хранятся в транспонированном виде, для построчного умножения матриц. Обратим внимание, что в списке параметров находится два смещения. На самом деле значащими параметрами является суммарный вектор bias_ih_l0 + bias_hh_l0. В исходниках поясняется, что: "Second bias vector included for CuDNN compatibility" (так видимо должно работать быстрее на графических картах).
Создадим случайный набор данных X и отправим его в рекуррентный слой. На выходе получится кортеж: тензор всех скрытых состояний формы (L,B,E) и тензор скрытого состояния последней ячейки (1,B,E):
X = torch.rand(L, B, E)
Y, Hn = rnn(X) # все выходы и последнее скрытое состояние
# (L, B, H) (1, B, H)
print(tuple(Y.shape), tuple(Hn.shape)) # (5, 4, 3) (1, 4, 3) Y[-1] == Hn[0]
Воспроизведём вычисления, происходящие внутри простого рекуррентного слоя. Для этого получим от объекта rnn значения параметров ячейки (отсоединив их от графа методом detach):
W_ih, W_hh = rnn.weight_ih_l0.detach(), rnn.weight_hh_l0.detach() B_ih, B_hh = rnn.bias_ih_l0.detach(), rnn.bias_hh_l0.detach()Скрытое состояние $\mathbf{h}^{(-1)}$, входящее в первую ячейку заполним нулями, как это делает по умолчанию nn.RNN.
В цикле "пробежимся по всем ячейкам" (метод addmm(v,M1,M2) вычисляет v + M1 @ M2):
Hn = torch.zeros(B,H) # начальное скрытое состояние - нули
for x in X: # по ячейкам for x:(B,E) in X:(L,B,E)
Hn =torch.tanh( torch.addmm(B_ih, x, W_ih.t())
+ torch.addmm(B_hh, Hn, W_hh.t()) )
print(Hn)
Начальное скрытое состояние можно передавать объекту сети вторым параметром (тогда оно будет ненулевое). Повторим предыдущие вычисления, подавая в rnn по одному входу последовательности:
Hn = torch.zeros(1,B,H) # начальное скрытое состояние - нули
for x in X:
_, Hn = rnn( x.view(1,B,E), Hn ) # Hn от предыдущей ячейки
print(Hn)
Слой Bidirectional и стопка слоёв
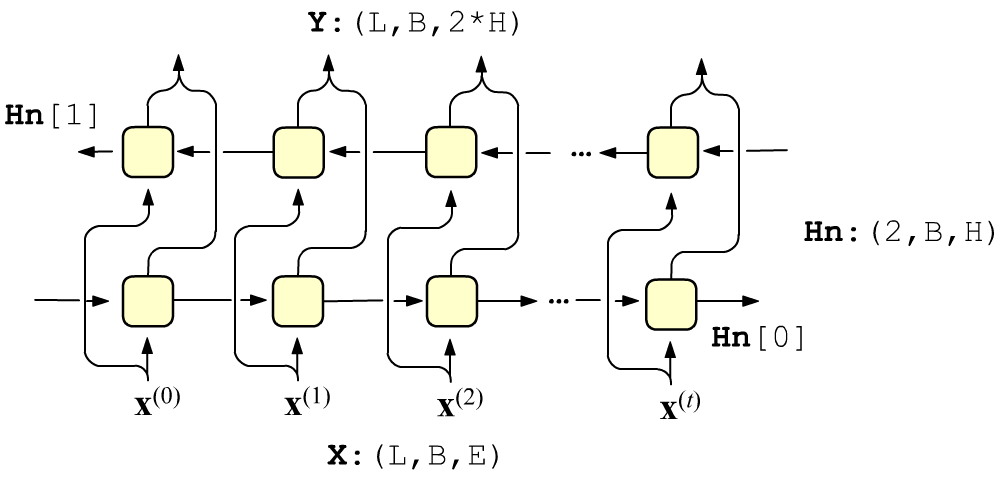 Иногда на настоящее влияет не только прошлое, но и будущее.
Например, смысл слова в предложении определяется всем предложением,
а не только предшествующими ему словами.
Иногда на настоящее влияет не только прошлое, но и будущее.
Например, смысл слова в предложении определяется всем предложением,
а не только предшествующими ему словами.
В этом случае уместно совместно использовать два рекуррентных слоя с различными параметрами. В первом слое скрытые состояния распространяются слева направо, а во втором - справа налево. Входные векторы подаются независимым образом на каждый слой, а выходы слоёв конкатенируются. Поэтому выходной тензор имеет размерность (L,B,2*H). Финальные скрытые состояния в Hn: (2,B,E) поступают от каждого слоя. При этом Hn[0] - это скрытое состояние последней (самой правой) ячейки первого слоя, а Hn[1] - первой (самой левой) ячейки второго слоя. В PyTorch двунаправленный слой создаётся так:
rnn = nn.RNN(E, H, bidirectional=True)
Рекуррентный слой (одиночный или двунаправленный) можно превратить в стопку слоёв:
 rnn = nn.RNN(E, H, num_layers=3)
rnn = nn.RNN(E, H, num_layers=3)
Положим Dir = 2 if bidirectional==True else 1.
Если число слоёв равно Num, тогда
входные и выходные тензоры в общем случае имеют следующие размерности:
X : (L, B, E) => Y : (L, B, Dir*H) H0: (Num*Dir, B, H) => Hn: (Num*Dir, B, H )
Упаковка последовательностей
Обучающие последовательности часто имеют различную длину. Например, число слов заметно меняется от предложения к предложению. Возможны различные стратегии работы с RNN в таких ситуациях.
Можно подавать на вход RNN по одной последовательности (B=1). Так как PyTorch строит динамические графы, необходимое число ячеек будет "создаваться на лету". Однако пропускание через сеть по одному примеру замедляет вычисления, особенно при использовании графических карт. Если разброс длин невелик, можно сортировать последовательности по длине и формировать батчи из примеров одинаковой длины.
Наконец, при формировании батчей можно воспользоваться функцией pack_padded_sequence, которая сама отсортирует примеры в батче по убыванию длины и для каждой ячейки сформирует максимально длинный батч.
from torch.nn.utils.rnn import pack_padded_sequence, pad_packed_sequenceПроиллюстрируем действие этой функции на примере. Пусть в батче B=4 обучающих примеров. Первый имеет длину 5, второй - 3, третий - 4 и четвёртый - 2. Примеры объединены в тензор, более короткие последовательности "добиваются" до максимальной длины L=5 нулевыми входными векторами (размерности E=2). Таким образом входной тензор X имеет форму (L,B,E)=(5,4,2):
X = torch.tensor([[1,1],[1,2],[1,3],[1,4],[1,5],
[2,1],[2,2],[2,3],[0,0],[0,0],
[3,1],[3,2],[3,3],[3,4],[0,0],
[4,1],[4,2],[0,0],[0,0],[0,0]],
dtype=torch.float)
X = X.view(B,L,E) # (B*L,E)->(B,L,E)
X = X.transpose(0,1) # -> (L,B,E)
Зададим длины примеров X_len (длины строк, если отбросить нули) и вызовем функцию упаковки:
X_len = torch.tensor([5,3,4,2])# длины примеров
Xp = pack_padded_sequence(X, # пакуем
X_len,
enforce_sorted=False)
PackedSequence(
data=tensor(
[[1., 1.],
[3., 1.],
[2., 1.],
[4., 1.], <- 1-я ячейка B=4
[1., 2.],
[3., 2.],
[2., 2.],
[4., 2.], <- 2-я ячейка B=4
[1., 3.],
[3., 3.],
[2., 3.], <- 3-я ячейка B=3
[1., 4.],
[3., 4.], <- 4-я ячейка B=2
[1., 5.]]),<- 5-я ячейка B=1
batch_sizes = tensor([4,4,3,2,1]),
sorted_indices = tensor([0,2,1,3]))
Теперь можно отправить упаковку в сеть: Yp, Hn = rnn(Xp). Последнее скрытое состояние Hn будет обычного размера (1,B,H)=(1,4,3). Выходы всех ячеек Yp, как и входы Xp, будут упакованы. Чтобы их распаковать, необходимо вызвать вторую функцию:
Y, Y_len = pad_packed_sequence(Yp)В результате получится что-то типа (теперь Y[-1] != Hn[0], т.к. Hn содержит последние не нулевые строки из всех выходов Y[i]):
Y[0] = [[-0.4083, 0.2363, 0.8988], | Y[-1]= [[-0.8162, 0.9937, 0.9942],
[-0.8875, -0.6924, 0.9849], | [ 0.0000, 0.0000, 0.0000],
[-0.7268, -0.2967, 0.9605], | [ 0.0000, 0.0000, 0.0000],
[-0.9561, -0.8852, 0.9943]] | [ 0.0000, 0.0000, 0.0000]]
Y_len = tensor([5, 3, 4, 2]) # тоже самое, что и X_len
Алгоритм работы RNN с упакованными данными воспроизводится следующим образом:
Hn = torch.zeros(Xp.batch_sizes[0], H) # нули в начальном состоянии
Yp = torch.empty(len(Xp.data), H) # упакованный тензор выходов ячеек
beg = 0
for bs in Xp.batch_sizes: # по размерам батчей
XX = Xp.data[beg: beg + bs] # батч текущей ячейки
HH = Hn[ : bs] # входящее в неё скрытое состояние
HH = torch.tanh( torch.addmm(B_ih, XX, W_ih.t()) # собственно вычисления
+ torch.addmm(B_hh, HH, W_hh.t()) )
Yp[beg: beg + bs].copy_(HH) # пакуем батч выхода
Hn[ : bs].copy_(HH) # накапливаем его в скр.состоянии
beg += bs
Hn = Hn[Xp.sorted_indices] # исходный порядок строчек
print(Yp, Hn) # совпадёт с Yp, Hn = rnn(Xp)
Кроме input=X и length у функций упаковки есть ещё два параметра. Если enforce_sorted = True, то батч должен быть отсортирован по убыванию длины последовательностей. Параметр batch_first = True предполагает, что входной тензор имеет форму (B,L,E). Этот же параметр тогда необходимо использовать в конструкторе RNN при создании экземпляра слоя.
Все параметры класса RNN
Приведём список всех параметров класса RNN в фреймворке PyTorch:
✒ nn.RNN
… (input_size,
hidden_size, num_layers=1, nonlinearity='tanh', bias=True,
… batch_first=False, dropout=0, bidirectional=False)
[doc]
Отметим не упомянутый ранее параметр dropout. По умолчанию он равен нулю. При ненулевом значении, после каждого слоя (num_layers > 1), кроме последнего, вставляется слой dropout, который с вероятностью dropout случайно "отключает" (делает нулевыми) часть элементов тензоров на выходах каждой ячейке.
Установка параметра bias в значение False ликвидирует вектор смещения после перемножения матриц.
Ячейка LSTM
В LSTM слое (long short-term memory), кроме скрытого состояния $\mathbf{h}$ между ячейками передаётся "состояние памяти" $\mathbf{c}$. Размерность H этого вектора совпадает с размерностью скрытого состояния $\mathbf{h}$. Векторы $\mathbf{c}$ регулируют какие признаки надо запомнить или забыть при передаче к следующей ячейке, что улучшает долгосрочную память.
Внутри LSTM-ячейки присутствует четыре линейных слоя с H нейронами. Три из них имеют сигмоидную активацию $\sigma$ (на выходе вектор со значениями $[0...1]$) и один слой с гиперболическим тангенсом $\tanh$: $[-1...1]$.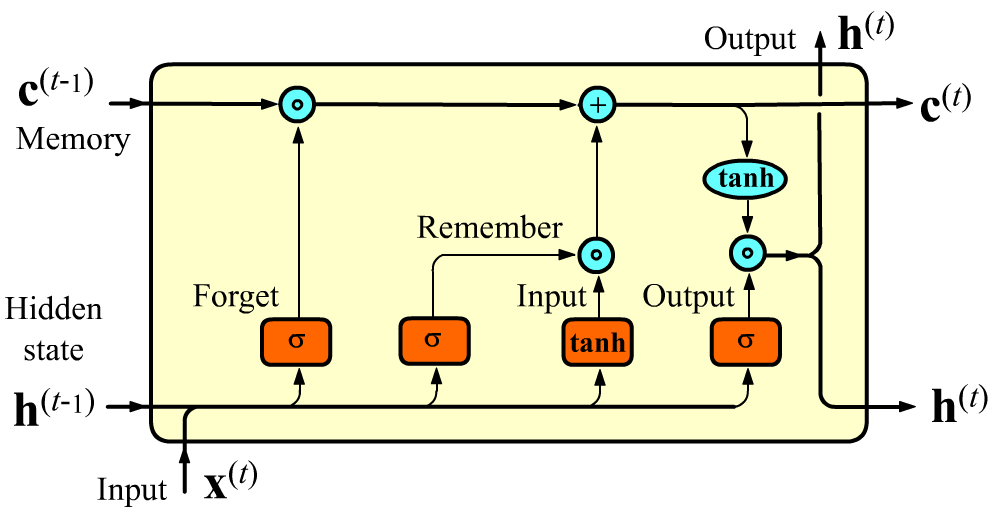
Перед этим вычислением происходит изменение значения входящего в ячейку вектора памяти $\mathbf{c}^{(t-1)}$. Сначала $\mathbf{x}^{(t)}, \mathbf{h}^{(t-1)}$ попадают в полносвязный слой Forget с сигмоидой (гейт забывания). Размерность выхода этого слоя равна H (как у $\mathbf{h}$ и $\mathbf{c}$). Этот вектор без свёртки умножается на компоненты предыдущего вектора памяти $\mathbf{c}^{(t-1)}$. Предполагается, что при умножении какие-то признаки в $\mathbf{c}^{(t-1)}$ забываются (если их умножили на 0), а какие-то двигаются дальше (если их умножили на 1). Пример забывания: "Он взял джин, а она взяла мартини" ("взяла" после "она" может забыть про "он"). Аналогично точка, как признак конца предложения, должна обнулить существенную часть компонент вектора памяти $\mathbf{c}^{(t)}$.
Похожим образом работают следующий гейт, реализующие запоминание. Те фичи которые необходимо запомнить добавляются в вектор $\mathbf{c}$. Слой с $\tanh$ [-1...1] формирует "фичи-кандидаты", а слой с сигмоидом [0...1] усиливает или ослабляет роль запоминаемой фичи. Аналитически вычисления в LSTM ячейке выглядят следующим образом: $$ \left\{ \begin{array}{lclclcl} \mathbf{F} &=& ~~~~~~\sigma(\mathbf{x}^{(t)}\, \mathbf{W}_{f} &+& \mathbf{h}^{(t-1)}\, \mathbf{H}_{f} &+& \mathbf{b}_f),\\ \mathbf{I} &=& ~~~~~~\sigma(\mathbf{x}^{(t)}\, \mathbf{W}_{i} &+& \mathbf{h}^{(t-1)}\, \mathbf{H}_{i} &+& \mathbf{b}_i),\\ \mathbf{R} &=& \text{tanh}(\mathbf{x}^{(t)}\, \mathbf{W}_{r} &+& \mathbf{h}^{(t-1)}\, \mathbf{H}_{r} &+& \mathbf{b}_r),\\ \mathbf{O} &=& ~~~~~~\sigma(\mathbf{x}^{(t)}\, \mathbf{W}_{o} &+& \mathbf{h}^{(t-1)}\, \mathbf{H}_{o} &+& \mathbf{b}_o), \end{array} \right. ~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} \mathbf{c}^{(t)} &=& \mathbf{F} \odot \mathbf{c}^{(t-1)} + \mathbf{R}\odot \mathbf{I},\\[2mm] \mathbf{h}^{(t)} &=& \tanh\bigr(\mathbf{c}^{(t)}\bigr) \odot \mathbf{O}. \end{array} \right. $$
Размерности матриц для E$=\dim(\mathbf{x}),~~$ H$=\dim(\mathbf{h}),~\dim(\mathbf{c})$ равны: $$ \mathbf{W}_{i}, ~\mathbf{W}_{f}, ~\mathbf{W}_{r}, ~\mathbf{W}_{o}:~~~\mathrm{(E, H)};~~~~~~~~~~ \mathbf{H}_{i}, ~\mathbf{H}_{f}, ~\mathbf{H}_{r}, ~\mathbf{H}_{o}:~~~\mathrm{(H, H)};~~~~~~~~~~ \mathbf{b}_i, ~\mathbf{b}_f, ~\mathbf{b}_r, ~\mathbf{b}_o: ~~~~\mathrm{(1, H)}. $$ В PyTorch LSTM-сеть реализует класс torch.nn.LSTM. В отличии torch.nn.RNN при прямом проходе возвращается три тензора: Y, Hd, Cn (скрытое состояние и вектор памяти имеют одинаковую размерность).Ячейка GRU
Управляемый рекуррентный блок (Gated Recurrent Units, GRU) является упрощённой версией LSTM при сравнимой вычислительной мощности. Он производит следующие вычисления: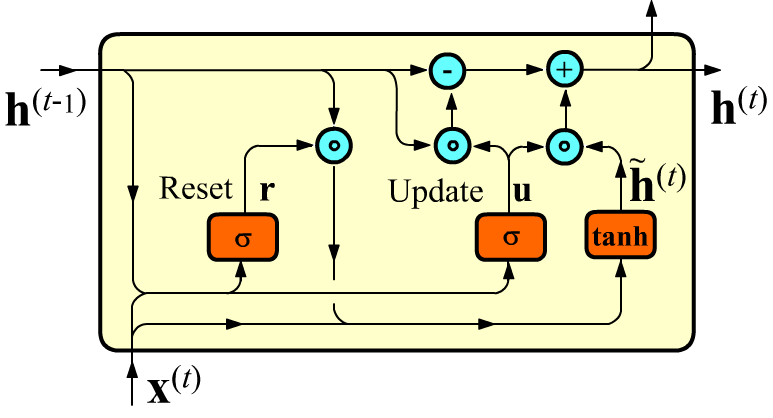
Распространение градиентов
Рассмотрим особенности распространения градиентов по рекуррентному слою во время его обучения. Поток градиентов существенно зависит от того, как вычисляется ошибка $L$, которая инициирует его запуск.
Будем для определённости прогнозировать очередную букву в тексте.
Пусть буквы векторизованы (эмбединг)
и поступают на вход слоя в виде последовательности L=5
векторов: $\{\mathbf{x}^{(0)},\mathbf{x}^{(1)},\mathbf{x}^{(2)},\mathbf{x}^{(3)},\mathbf{x}^{(4)}\}$.
Выход последней ячейки можно направить в полносвязный слой (с числом нейронов равных числу букв) и затем пропустить через функцию
softmax, дающую "вероятности" очередной буквы $\mathbf{x}^{(5)}$.
В более общем случае можно обучать сеть предсказывать буквы на нескольких последних ячейках (ниже - это последние три выхода $\{\mathbf{x}^{(3)},\mathbf{x}^{(4)},\mathbf{x}^{(5)}\}$). На выходе последней ячейке мы по-прежнему ожидаем получить $\mathbf{x}^{(5)}$, а на предыдущих двух выходах - последние "входные" буквы , но смещённые назад. На первых двух ячейках слой накапливает в скрытом состоянии историю, а затем начинает предсказания, "продолжая" накопление истории:
Ошибки равны логарифмам вероятностей (с обратным знаком) "правильных" букв. От каждой из трёх букв эти ошибки суммируются, что даёт суммарную ошибку $L$. При обратном распространении, градиент $g=1$ из $L$, расщепившись, спускается вниз, проходя через софтмакс-функцию и линейный слой, попадают на выходы последних трёх ячеек. Затем, пройдя через ячейки, градиенты двигаются влево по слою.
Набор параметров RNN-ячейки на правом рисунке обозначен вектором $\mathbf{w} = \{\mathbf{W},\mathbf{H},\mathbf{b},...\}$. Так как для всех ячеек эти параметры одни и те-же, градиенты из ячеек попадают в $\mathbf{w}$ и там суммируются.
Обратим внимание, что в последнюю (5-ю) ячейку заходит суммарный градиент меньший чем в 4-ю и 3-ю, т.к. в него не попадает градиент в горизонтальном направлении.
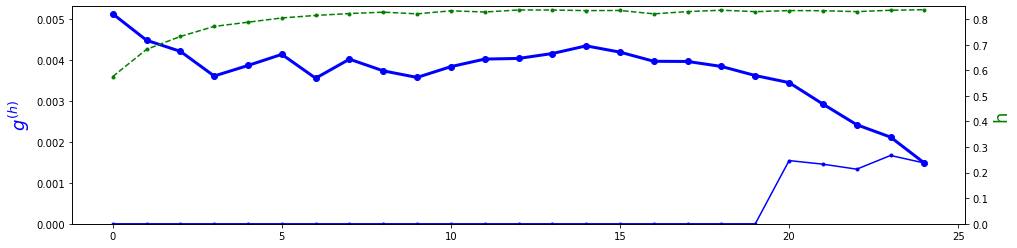
Ниже представлен реальный пример изменения вдоль RNN-слоя длины градиента усреднённого по батчу. У слоя L=25 ячеек и ошибка вычисляется по последним 5 выходам (E=10, H=50, один слой, GRU-ячейки). Жирная синяя линия - это суммарный градиент входящий в ячейку (сверху и справа); тонкая линия - градиент входящий только сверху и пунктирная зелёная - средняя длина вектора скрытого состояния. График соответствует началу обучения:
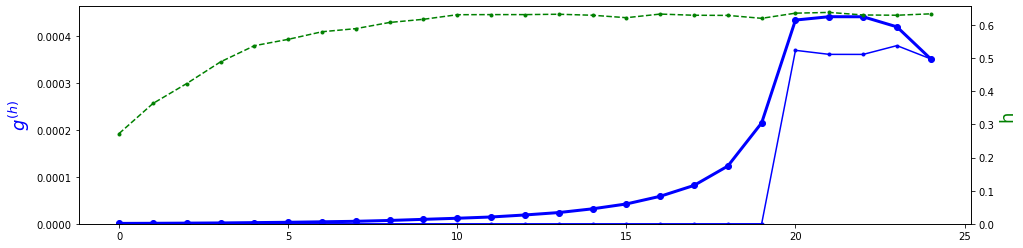
Если смотреть на график справа-налево, видно, что градиент сначала начинает подрастать (к "вертикальным" градиентам добавляются "горизонтальные"). Затем, когда "впрыскивание" вертикальных градиентов от ошибок прекращается, градиент монотонно затухает к началу последовательности (vanishing gradient problem).
Такая ситуация типична в начале обучения (после первой эпохи loss: trn=3.07 val=2.78). Когда сеть обучена после 30 эпохи loss: trn=1.12 val=1.10, затухание градиента может пропадать (среднее значение по модулю элементов матриц $H$, сворачивающихся со скрытым состоянием увеличивается с 0.12 до 0.42).
Градиенты в ячейках
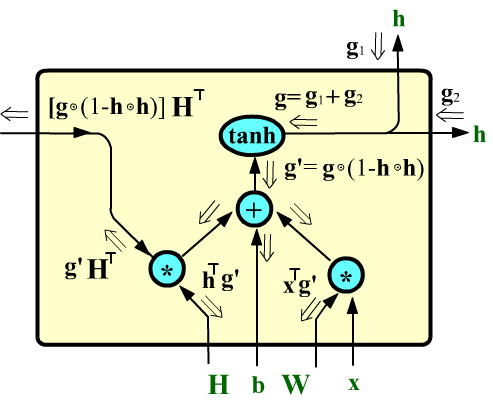 Пусть в простую ячейку nn.RNN справа, по линии скрытого состояния входит градиент $\mathbf{g}$.
Производная от гиперболического тангенса $\tanh (x)$ равна $1-\tanh^2(x)$.
На выходе узла тангенса на этапе прямого прохождения получился вектор $\mathbf{h}$.
Поэтому пройдя узел $\tanh$, компоненты градиента умножаться на
$1-\mathbf{h}\odot \mathbf{h}$, где символ $\odot$ - это умножение без свёртки:
$(\mathbf{u}\odot\mathbf{v})_i = u_i v_i$.
Пусть в простую ячейку nn.RNN справа, по линии скрытого состояния входит градиент $\mathbf{g}$.
Производная от гиперболического тангенса $\tanh (x)$ равна $1-\tanh^2(x)$.
На выходе узла тангенса на этапе прямого прохождения получился вектор $\mathbf{h}$.
Поэтому пройдя узел $\tanh$, компоненты градиента умножаться на
$1-\mathbf{h}\odot \mathbf{h}$, где символ $\odot$ - это умножение без свёртки:
$(\mathbf{u}\odot\mathbf{v})_i = u_i v_i$.
Учитывая правила преобразования градиентов на узлах элементарных операций, получаем, что на выходе ячейки градиент равен $[\mathbf{g}\odot (1-\mathbf{h}\odot \mathbf{h})]\cdot \mathbf{H}^\top$. Если $\mathbf{h}$ близок к $\pm 1$, то градиент будет уменьшается. Аналогично уменьшают его малые компоненты матрицы $\mathbf{H}$.
После прохождения n ячеек градиент, попадающий внутрь первой ячейки будет умножен на фактор типа: $$ \mathbf{g}' = \bigr[\bigr[...\bigr[\mathbf{g}^{(n)} \odot (1-\mathbf{h}^{(n)}\odot \mathbf{h}^{(n)})\cdot \mathbf{H}^\top\bigr] \odot (1-\mathbf{h}^{(n-1)}\odot \mathbf{h}^{(n-1)})\cdot \mathbf{H}^\top\bigr]\,\odot ... \odot\, (1-\mathbf{h}^{(1)}\odot \mathbf{h}^{(1)})\bigr] \cdot \mathbf{H}^\top $$ Так как параметры всех ячеек одинаковы, входяшие в них градиенты необходимо сложить. Наиболее значимыми будут градиенты от последних ячеек если ошибка вычисляется только к последнему скрытому состоянию (т.е. градиент от ошибки входит только в последнюю ячейку).
Одна из возможных стратегий борьбы с затуханием состоит в том, что обучение начинается с учёта ошибок выходов всех ячеек. Затем, по мере обученности сети, учитываются только ошибки последних ячеек. Можно также увеличивать дисперсию начальных случайных значений матрицы $\mathbf{H}$.
Напомним, что в стопке полносвязных слоёв затухание градиента приводит к полной остановке обучения. В рекуррентном слое проблема затухания не столько серьёзная. Так как у всех ячеек параметры одни и те же, они будут в любом случае меняться за счёт градиета в последних ячейках
Дополнительное чтение :
- The Unreasonable Effectiveness of Recurrent Neural Networks
- Understanding LSTM Networks
- Building a LSTM by hand on PyTorch
- Как научить свою нейросеть генерировать стихи
