ML: Рекуррентные сети на Keras

Введение

Иногда обучающие данные являются упорядоченной последовательностью. Например, временные ряды (котировки акций, показания сенсора) или последовательность слов естественного языка. В этих случаях имеет смысл использовать рекуррентные нейронные сети RNN (recurrent neural network).

В качестве примеров на Python ниже мы будем использовать библиотеки numpy и keras: 

import numpy as np                                # работа с тензорами

from keras.models import Sequential, Model
from keras.layers import SimpleRNN, LSTM, Dense, Embedding, Concatenate, Bidirectional
Все примеры можно найти в файле:ML_RNN_Keras.ipynb. Обсуждение RNN на фреймворке PyTorch можно найти здесь.

SimpleRNN

Простая рекуррентная сеть состоит из inputs связанных ячеек с одинаковыми параметрами. Сеть получает упорядоченную последовательность длинной inputs. Каждый элемент последовательности является f-мерным вектором $\mathbf{x}=\{x_0,...,x_{f-1}\}$ признаков (features). Первый вектор поступает на вход первой ячейки, второй - на вход второй и т.д. Каждая ячейка характеризуется units-мерным вектором скрытого состояния: $\mathbf{h}=\{h_0,...,h_{u-1}\}$. Этот вектор является выходом ячейки (стрелка вверх), и он же отправляется в следующую ячейку. Внутри ячейки проводится следующее вычисление:

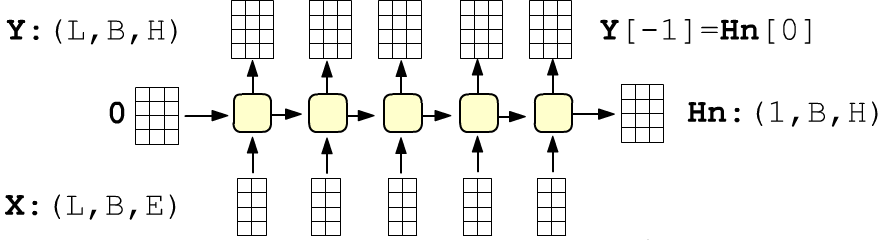
$$ \begin{array}{rcl} \mathbf{h}^{(t)} &=& f(\mathbf{x}^{(t)},\mathbf{h}^{(t-1)}) \\[3mm] &=& \tanh(\mathbf{x}^{(t)}\cdot \mathbf{W} + \mathbf{h}^{(t-1)}\cdot \mathbf{H} + \mathbf{b}) \end{array} $$

Так как все ячейки одинаковые, число входов inputs на число параметров не влияет. Размерности (shape) матриц равны: $\mathbf{W}:$(features, units), $~\mathbf{H}:$(units, units), $~\mathbf{b}:$( units, ), а общее число параметров: 

   params = (features + units + 1) * units

Начальный вектор скрытого состояния $\mathbf{h}^{(-1)}$ (входящий в первую ячейку) или равен нулю $\mathbf{0}$, или полагается равным скрытому состоянию последней ячейки на примере предыдущей последовательности (или батче последовательностей). Рассмотрим подробнее матричные умножения при вычислении скрытого состояния.

Матричные умножения

Фактически в RNN ячейке входной вектор $\mathbf{x}^{(t)}$ и вектор скрытого состояния предыдущей ячеки $\mathbf{h}^{(t-1)}$ объединяются (конкатенируются) и пропускаются через полносвязный слой с функцией активации than. На его выходе и получается скрытое состояние текущей ячейки. Рассмотрим подробнее как происходят матричные вычисления.

Вектор признаков $\mathbf{x}_t$, как обычно, умножается на матрицу весов $\mathbf{W}$ слева, чтобы можно было добавлять к нему строки батча. Например для размерности входа features=3 и размерности выхода (скрытого состояния) units=2 имеем:

$$ \begin{array}{|c|c|c|} \hline x^{(t)}_{0} & x^{(t)}_{1} & x^{(t)}_{2} \\ \hline \end{array} \cdot \begin{array}{|c|c|} \hline W_{00} & W_{01} \\ \hline W_{10} & W_{11} \\ \hline W_{20} & W_{21} \\ \hline \end{array} ~~ + ~~ \begin{array}{|c|c|} \hline h^{(t-1)}_{0} & h^{(t-1)}_{1} \\ \hline \end{array} \cdot \begin{array}{|c|c|} \hline H_{00} & H_{01} \\ \hline H_{10} & H_{11} \\ \hline \end{array} ~~+~~ \begin{array}{|c|c|} \hline b_{0} & b_{1} \\ \hline \end{array} ~~=~~ \begin{array}{|c|c|} \hline r^{(t)}_0 & r^{(t)}_1 \\ \hline \end{array} $$

Подобное матричное умножение можно сделать более компактным, произведя конкатенацию векторов $\mathbf{x}^{(t)}$, $\mathbf{h}^{(t-1)}$ и присоеденив матрицу $\mathbf{H}$ к матрице $\mathbf{W}$ снизу:

$$ \begin{array}{|c|c|c|c|c|} \hline x^{(t)}_{0} & x^{(t)}_{1} & x^{(t)}_{2} & h^{(t-1)}_{0} & h^{(t-1)}_{1}\\ \hline \end{array} \cdot \begin{array}{|c|c|} \hline W_{00} & W_{01} \\ \hline W_{10} & W_{11} \\ \hline W_{20} & W_{21} \\ \hline H_{00} & H_{01} \\ \hline H_{10} & H_{11} \\ \hline \end{array} ~~+~~ \begin{array}{|c|c|} \hline b_{0} & b_{1} \\ \hline \end{array} ~~=~~ \begin{array}{|c|c|} \hline r^{(t)}_0 & r^{(t)}_1 \\ \hline \end{array} $$

Именно в этом смысле выше нарисованы слитые в одну стрелки векторов $\mathbf{x}^{(t)},\mathbf{h}^{(t-1)}$. Вычислив гиперболический тангенс от результата перемножения $\mathbf{r}^{(t)}$, мы получим вектор скрытого состояния $\mathbf{h}^{(t)}= \tanh(\mathbf{r}^{(t)})$. Если умножение производится сразу для всех примеров батча, то они добавляются как строки (ниже batch_size=3):

$$ \begin{array}{|c|c|c|c|c|} \hline x^{(t)}_{00} & x^{(t)}_{01} & x^{(t)}_{02} & h^{(t-1)}_{00} & h^{(t-1)}_{01}\\ \hline x^{(t)}_{10} & x^{(t)}_{11} & x^{(t)}_{12} & h^{(t-1)}_{10} & h^{(t-1)}_{11}\\ \hline x^{(t)}_{20} & x^{(t)}_{21} & x^{(t)}_{22} & h^{(t-1)}_{20} & h^{(t-1)}_{21}\\ \hline \end{array} \cdot \begin{array}{|c|c|} \hline W_{00} & W_{01} \\ \hline W_{10} & W_{11} \\ \hline W_{20} & W_{21} \\ \hline H_{00} & H_{01} \\ \hline H_{10} & H_{11} \\ \hline \end{array} ~~+~~ \begin{array}{|c|c|} \hline b_{0} & b_{1} \\ \hline \end{array} ~~=~~ \begin{array}{|c|c|} \hline r^{(t)}_{00} & r^{(t)}_{01} \\ \hline r^{(t)}_{10} & r^{(t)}_{11} \\ \hline r^{(t)}_{20} & r^{(t)}_{21} \\ \hline \end{array} $$

В этом случае строка смещения $(b_1~b_2)$ формы (1,2) прибавляется к каждой строке матрицы формы (3,2), по правилу расширения (broadcasting), принятого в numpy.

SimpleRNN в Keras

При создании рекуррентного слоя обязательно указывается размерность скрытого состояния units и (если слой первый) размерности входных векторов features (не первый слой получит их от предыдущих слоёв): 

units    = 4          # размерность скрытого состояния   = dim(h)
features = 2          # размерность входов               = dim(x)
inputs   = 3          # число входов (ячек RNN слоя)

model = Sequential()                  
model.add(SimpleRNN(units=units, input_shape=(inputs, features))) # Output Shape: (None, 4)
По умолчанию такой слой возвращает скрытое состояние только последней ячейки слоя (см. следующий раздел). Поэтому тензор, который возвращает слой имеет размерность (None, units) и не зависит от числа входов (ячеек) inputs и их размерности features. None соответствует произвольному числу примеров в батче.

Так как все ячейки одинаковые, число входов можно не указывать, поставив None: 

model = Sequential()     
model.add(SimpleRNN(units=units, input_shape=(None, features)))   # Output Shape: (None, 4)
Тогда одна и та же модель может обрабатывать не только различные батчи, но и батчи с полследовательностями разной длины (но одной для каждого примера данного батча): 
                         
model.predict( np.zeros( (2, 3, features)  ))
model.predict( np.zeros( (2, 4, features)  ))

В первом predict батч из двух "примеров" c тремя входами. Во втором примеры батча с четырьмя входами.

Иногда при определении модели необходимо жёстко задать размер батча. Тогда, как обычно, используем параметр batch_input_shape вместо input_shape: 

                         
model = Sequential()
model.add(SimpleRNN(units=units, batch_input_shape=(10, inputs, features)))  #    (10, 4)

Many-to-one или Many-to-many

Рекуррентный слой, может возвращать скрытое состояние только последней ячейки (return_sequences = False) или скрытые состояния всех ячеек слоя (return_sequences = True):

В зависимости от режима, изменяется размерность выхода рекуррентного слоя. Если return_sequences = True (все ячейки возвращают), то размерность выхода слоя это (batch_size, inputs, units): 

model = Sequential()
model.add(SimpleRNN(units=4, input_shape=(None,2), return_sequences = True ))

Output Shape: (None, None, 4)
При return_sequences = False (в Keras по умолчанию), то размерность выхода слоя это (batch_size, units): 
model = Sequential()
model.add(SimpleRNN(units=4, input_shape=(None, 2), return_sequences = False ))

Output Shape:  (None, 4)
Число параметров слоя (в данном примере 28) от значения return_sequences не зависит (это число элементов матриц ячейки).

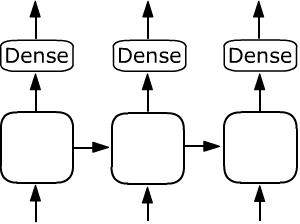Если после рекуррентного слоя с return_sequences = True стоит, например, полносвязный слой Dense, то он с одними и теми же параметрами применяется к выходу каждой ячейки: 

model = Sequential()
model.add(SimpleRNN(units=4, input_shape=(None,2), return_sequences=True))
model.add(Dense(units=8))

Output Shape: (None, None, 8)
Таким образом на выходе имеем матрицу (batch_size, rnn_inputs, dense_units). Вектор скрытого состояния $\mathbf{h}$ каждой ячейки проходя через слой Dense переходит в вектор другой размерности (выше dense_units=8). Если бы было return_sequences = False, то на выходе модели была бы матрица (batch_size, dense_units).

Аналогичным образом, вместо Dense, можно использовать другие рекуррентные слоя, создавая из них стопку для глубокого обучения.

Ещё немного параметров

При задании рекурентного слоя доступны также следующие параметры:

Игрушечный пример

Рассмотрим линейную модель $h_t = x_t+ h_{t-1}$ (все "векторы" в ней однокомпонентны, поэтому временные индексы пишем внизу). В качестве входов $x_t$ будем использовать два батча по одному примеру в каждом $\{1,2,3\}$ и $\{4,5,6\}$. Если мы работаем в режиме stateful = False, то перед каждым батчем $h_{-1}=0$. Когда stateful = True, для первого батча $h_{-1}=0$, а для второго $h_{-1}$ равно последнему скрытому состоянию:

$$ \begin{array}{ll} \mathrm{stateful} & \mathrm{=~False} \\ x_0 = 1, & h_1 = x_0 + h_0 = 1 + \mathbf{0} = 1\\ x_1 = 2, & h_2 = x_1 + h_1 = 2 + 1 = 3\\ x_2 = 3, & h_3 = x_3 + h_2 = 3 + 3 = \mathbf{6}\\ \hline x_0 = 4, & h_4 = x_0 + h_3 = 4 + \mathbf{0} = 4\\ x_1 = 5, & h_2 = x_1 + h_1 = 5 + 4 = 9\\ x_2 = 6, & h_3 = x_3 + h_2 = 6 + 9 = \mathbf{15}\\ \end{array} $$
$$ \begin{array}{ll} \mathrm{stateful} & \mathrm{=~True} \\ x_0 = 1, & h_1 = x_0 + h_0 = 1 + \mathbf{0} = 1\\ x_1 = 2, & h_2 = x_1 + h_1 = 2 + 1 = 3\\ x_2 = 3, & h_3 = x_3 + h_2 = 3 + 3 = \mathbf{6}\\ \hline x_0 = 4, & h_4 = x_0 + h_3 = 4 + \mathbf{6} = 10\\ x_1 = 5, & h_2 = x_1 + h_1 = 5 + 10 = 15\\ x_2 = 6, & h_3 = x_3 + h_2 = 6 + 15 = \mathbf{21}\\ \end{array} $$

Проделаем эти вычисления при помощи рекуррентной сети: 

model = Sequential()
model.add(SimpleRNN(units=1, batch_input_shape=(1, 3, 1), 
                    activation="linear", stateful = True, name='rnn') )
Так как по умолчанию return_sequences=False, сеть будет возвращать скрытое состояние только последней ячейки (выше в примере цифры жирным шрифтом).

Зададим значения "матриц" рекуррентной ячейки. В нашем примере $\mathbf{W}$ и $\mathbf{H}$ состоят из одного элемента и имеют форму (1,1). Смещение $\mathbf{b}$ равно нулю. Параметры в слое упакованы в список в порядке [ W, H, b ]: 

W, H, b  = np.array([[1]]), np.array([[1]]), np.array([0])
model.get_layer('rnn').set_weights(([ W, H, b ]))              # меняем веса
Теперь можно проводить вычисления: 
res = model.predict(np.array([ [ [1], [2], [3] ]  ] )) 
print("res:",np.reshape(res, -1) )                             # res: [6.]

res = model.predict(np.array([ [ [4], [5], [6] ]  ] )) 
print("res:",np.reshape(res, -1) )                             # res: [21.]
Если положить stateful = False, то результаты будут равны 6 и 15.

LSTM

Стандартные RNN плохо справляются с "договременными зависимостями" и в основном ловят корреляции между соседними членами последовательности. С долговременными зависимостями лучше справляется рекуррентный слой с LSTM ячейками.

Кроме скрытого состояния $\mathbf{h}$ от ячейки к ячейки в LSTM слое передаётся состояние памяти $\mathbf{c}$. Этот вектор имеет размерность units, как и обычное скрытое состояние $\mathbf{h}$. Векторы $\mathbf{c}$ регулируют какие фичи надо забыть, а какие запомнить при передаче к следующей ячейке. При помощи этого потока реализуется долгосрочная память.

Внутри LSTM-ячейки, вместо одного слоя нейронной сети (как в SimpleRNN), существует четыре слоя. Сигмоидные слои $\sigma$ на выходе имеют вектор со значениями $[0...1]$, а гиперболический тангенс $\tanh$ - со значениями $[-1...1]$.

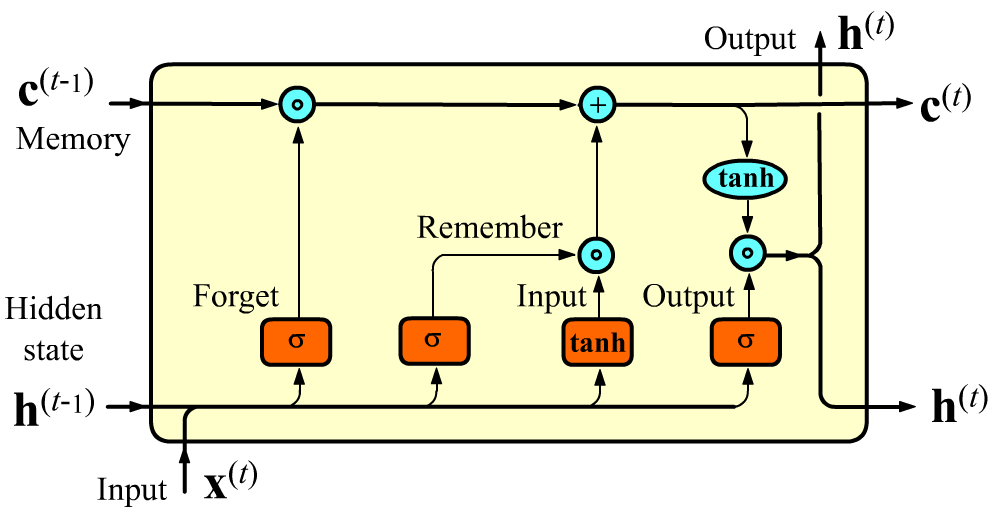
$$ \left\{ \begin{array}{lcl} \mathbf{h}_t &=& \tanh(\mathbf{c}_{t}) * f(\mathbf{x}_t,\,\mathbf{h}_{t-1}),\\[3mm] \mathbf{c}_t &=& g(\mathbf{x}_t,\,\mathbf{h}_{t-1},\, \mathbf{c}_{t-1}) \end{array} \right. $$

Скрытое состояние $\mathbf{h}$ вычисляется аналогично SimpleRNN (но с сигмоидой вместо $\tanh$, см. последний прямоугольник). После этого он умножается на $\tanh(\mathbf{c})$. Гиперболический тангенс берётся независимо от каждой компоненты вектора $\mathbf{c}$, делая при умножении соответствующую компоненту $\mathbf{h}$ положительной или отрицательной (или, возможно, её зануляя, если данная фича-компонента не важна для дальнейшего).

Перед этим вычислением происходит изменение значения вектора памяти $\mathbf{c}^{(t-1)}$. Сначала $\mathbf{x}^{(t)}, \mathbf{h}^{(t-1)}$ попадают в полносвязный слой с сигмоидой [0...1] на выходе. Он называется гейтом забывания. Размерность выхода этого слоя равна units (это размерность $\mathbf{h}$ и $\mathbf{c}$). Компоненты выходного вектора умножаются на компоненты предыдущего вектора памяти $\mathbf{c}^{(t-1)}$ (без свёртки!). При умножении какие-то признаки в $\mathbf{c}^{(t-1)}$ забываются (если умножили на 0), а какие-то двигаются дальше (если их умножили на 1). Пример необходимости забывания: "She put on a red hat and a green skirt" ("green" после существительного может забыть "red")

Похожим образом работают следующие два гейта, реализующие запоминание. Те фичи которые необходимо запомнить добавляются в вектор $\mathbf{c}$. Слой с $\tanh$ формирует "фичи-кандидаты", масштабируя их в интервал [-1...1]. Слой с сигмоидом [0...1] усиливает или ослабляет роль запоминемой фичи.

Более детально, вычисления в LSTM ячейке выглядят следующим образом: $$ \left\{ \begin{array}{lclclcl} \mathbf{F} &=& ~~~~~~\sigma(\mathbf{x}^{(t)}\, \mathbf{W}_{f} &+& \mathbf{h}^{(t-1)}\, \mathbf{H}_{f} &+& \mathbf{b}_f),\\ \mathbf{I} &=& ~~~~~~\sigma(\mathbf{x}^{(t)}\, \mathbf{W}_{i} &+& \mathbf{h}^{(t-1)}\, \mathbf{H}_{i} &+& \mathbf{b}_i),\\ \mathbf{R} &=& \text{tanh}(\mathbf{x}^{(t)} \mathbf{W}_{r} &+& \mathbf{h}^{(t-1)}\, \mathbf{H}_{r} &+& \mathbf{b}_r),\\ \mathbf{O} &=& ~~~~~~\sigma(\mathbf{x}^{(t)}\, \mathbf{W}_{o} &+& \mathbf{h}^{(t-1)}\, \mathbf{H}_{o} &+& \mathbf{b}_o), \end{array} \right. ~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} \mathbf{c}^{(t)} &=& \mathbf{F} * \mathbf{c}^{(t-1)} + \mathbf{I} * \mathbf{R},\\[2mm] \mathbf{h}^{(t)} &=& \tanh\bigr(\mathbf{c}^{(t)}\bigr) * \mathbf{O}. \end{array} \right. $$

Размерности матриц равны [feature$=\dim(\mathbf{x}),~~~~$ units$=\dim(\mathbf{h}),~\dim(\mathbf{c})$]: $$ \begin{array}{llllll} \mathbf{W}_{i}, &\mathbf{W}_{f}, &\mathbf{W}_{r}, &\mathbf{W}_{o}: &\mathrm{(features, units)},\\ \mathbf{H}_{i}, &\mathbf{H}_{f}, &\mathbf{H}_{r}, &\mathbf{H}_{o}: &\mathrm{(units, units)},\\ \mathbf{b}_i, &\mathbf{b}_f, &\mathbf{b}_r, &\mathbf{b}_o: &\mathrm{(1, units)}. \end{array} $$

Bidirectional слой

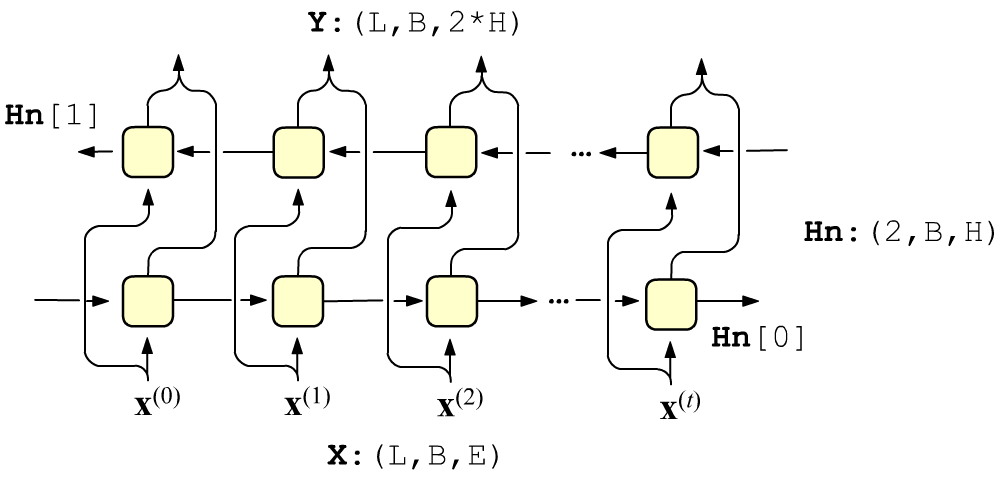Иногда в последовательностях существует влияние на настоящее не только прошлого, но и будущего. Например, смысл данного слова в предложении определяется всем предложением, а не только предшествующими до него словами.

В этом случае уместно совместно использовать два рекуррентных слоя, в первом из которых скрытые состояния распространяются слева направо, а в следующем слое - справа налево. Входные векторы подаются независимым образом на каждый слой, а их выходы конкатенируются. Веса ячеек каждого слоя различны.

Если return_sequences = False, то, как и ранее, на выход Bidirectional слоя поступает только конкатенация выходов последних ячеек каждого слоя. 

VOC_SIZE, VEC_DIM, inputs = 100, 8, 3

model = Sequential()  
model.add(Embedding(input_dim=VOC_SIZE, output_dim=VEC_DIM, input_length=inputs)) 

model.add(Bidirectional(SimpleRNN(units=4, return_sequences=True)))      # (None,3,8)

model.add(Dense(units = 1, activation='sigmoid'))                        # (None,3,1)

Выше первым стоит слой Embedding который получает размер словаря VOC_SIZE и размерность векторного пространства VEC_DIM и создаёт 2-мерный массив (VOC_SIZE, VEC_DIM). Embeddibg переводит целое число на входе (индекс слова) в вектор, который соответствует этому слову на выходе. В Embedding можно задавать число входов input_length, и тогда оно, как и число примеров в пачке (batch_size), считается неопределённым (сеть может обрабатывать любое количество входов).

Три вектора (inputs=3) размерности VEC_DIM=8 подаются на 3 входа Bidirectional слоя. Так как размерность скрытого состояния units=4, то на входе каждой ячейки будет по 8-мерному вектору (конкатенация 4+4=8).

Параметр return_state

При функциональном определении сети, можно вернуть не только выходы ячеек, но и все скрытые состояния последней ячейки 

units    = 4                   # размерность скрытого состояния   = dim(h)
features = 2                   # размерность входов               = dim(x)
inputs   = 3                   # число входов (ячек RNN слоя)

inp    = Input( shape=(inputs, features) )
rnn    = LSTM (units, return_sequences=True, return_state=True)(inp)

model  = Model(inp, rnn)       #   [(None, 3, 4), (None, 4), (None, 4)]
Список матриц соответствует всем выходам (return_sequences=True), скрытому состоянию h и скрытому состоянию памяти c. 
inp    = Input(shape=(inputs, features) )
rnn    = LSTM (units, return_sequences = True, return_state=True)

_,h,s  = rnn(inp)              # игнорируем выходы (первая матрица)

con    = Concatenate()([h,s])  # (None, 8)

model  = Model(inp, con)

В случае двунаправленного слоя 

inp    = Input(shape=(inputs, features) )
rnn    = LSTM (units, return_sequences = True, return_state=True)
bid    = Bidirectional(rnn)(inp)

Output shape: [(None, 3, 8), (None, 4), (None, 4), (None, 4), (None, 4)]